絞合式光纖的微彎損耗機制及其應用研究

茶國智

（大理學院工程學院，云南大理 671003）

絞合式光纖的微彎損耗機制及其應用研究

茶國智

（大理學院工程學院，云南大理 671003）

深入研究絞合式光纖的微彎損耗機制，提出兩種微彎損耗模型且給出了相應的理論表達式，經理論分析和數值模擬表明兩種模型都具有一定的合理性。同時，還對絞合式光纖的傳感檢測應用做了一些探討。

絞合式光纖；微彎損耗機制；微彎損耗應用

利用光纖的微彎損耗可以實現傳感檢測，在醫療、交通、電力、機械、航空航天等各個領域都有廣泛的應用前景。據此，下面擬對一種特殊的梯度型光纖微彎損耗——絞合式光纖微彎損耗進行研究。

1 微彎結構和損耗機制

1.1 微彎結構 將兩光纖間進行絞合，其形狀如圖1。絞合處就會形成光纖的微彎曲，在此微彎曲處將產生微彎損耗。

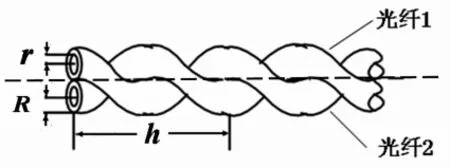
圖1 光纖絞合形狀

任一光纖微彎曲的幾何形狀實際上為圓柱螺旋線形，圖中r、R分別表示纖芯半徑和光纖半徑，h表示絞合螺距。在下面的處理中將一個螺距的絞合光纖段稱為一個微彎段（簡稱微彎）。整個絞合段由這樣的若干個微彎構成。

1.2 損耗機制

1.2.1 余弦曲率脈沖模型

1.2.1.1 微彎的曲率脈沖模型——余弦型 設理想光纖軸與坐標系z軸重合，則此時光纖軸的第n個微彎（段）可由螺旋線方程表示為：x=Rcos θ，y=Rsin θ，z=hθ/2π，其中θ表示螺旋線升角且取2nπ≤θ＜2（n+1）π，R、h的含義同前述。則此時光纖軸的第n個隨機微彎可用橫向（即x和y向）上偏離z軸的距離（fz）和g（z）來描述：

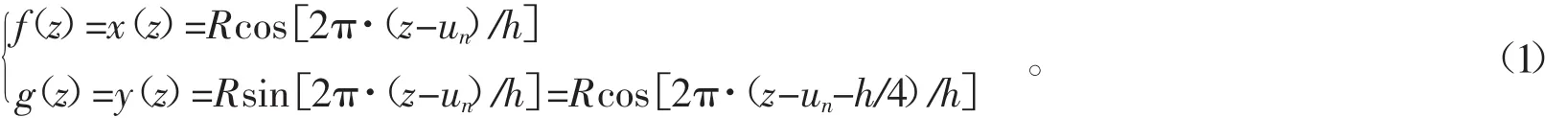
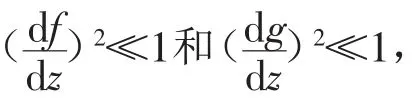
絞合段內N個微彎曲率函數稱為一系列曲率脈沖，并可根據曲率函數公式推導出這些曲率脈沖，可表示為：

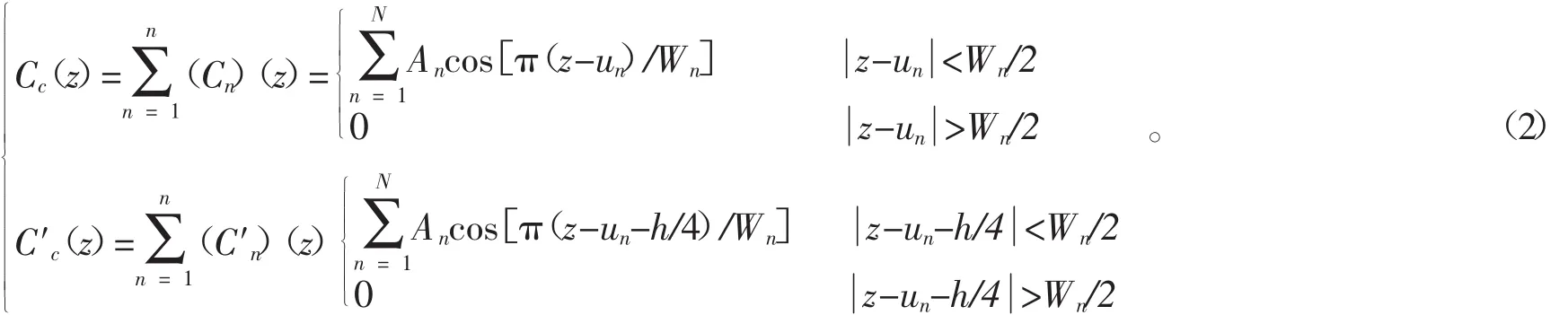
可見這些微彎的曲率脈沖為余弦型。在（2）式中下角標字母C表示余弦型，C（nz）和C′（nz）表示第n個微彎在x和y向的曲率函數，An為其曲率脈沖峰值，Wn為其曲率脈沖寬度。

1.2.1.2 功率譜密度 根據功率譜密度的定義〔1-2〕，可求得曲率函數的功率譜密度，故與（2）式相應的功率譜密度為：

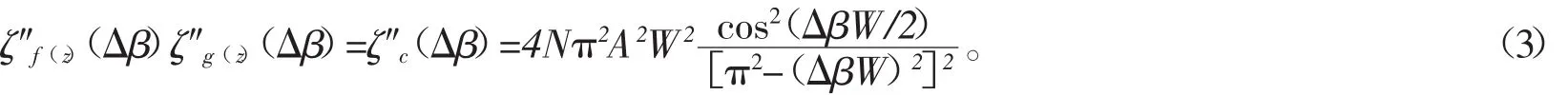
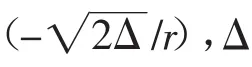
1.2.1.3 微彎損耗 文獻〔1〕給出了梯度多模光纖微彎發生在一個平面（二維）內時的損耗公式，而未給出發生三維微彎時的損耗式。但是可經過一系列繁瑣的推導，得到適用于圓柱螺旋形微彎的損耗式：

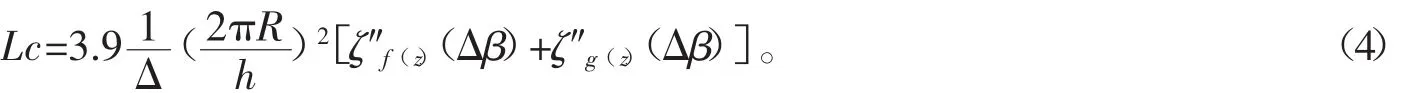
將式（3）代入（4）式得：

可見，當△、r、R一定時，損耗取決于N、h。

注：該模型作者已在文獻〔3〕中提出，此處稍作形式上的變換。下面提出另外一種新的模型。

1.2.2 矩形曲率脈沖模型

1.2.2.1 微彎的曲率脈沖模型——矩形型 圓柱螺旋線具有一個重要特性：其各點曲率都相同。如前所述絞合光纖微彎曲的幾何形狀為圓柱螺旋線形，則根據螺旋線方程可推知微彎處各點曲率都為：A=4π2R［/h2+（2πR）2］。根據這一特點，可假想將每個三維的圓柱螺旋線微彎段展開為一段二維的圓弧（因圓弧各點的曲率也相同），即三維變為二維。由于實際絞合光纖形成的圓柱螺旋線的饒率較小，因此這種設想是合理的。

微彎視為二維圓弧后，絞合段內N個微彎曲率函數（亦可稱為曲率脈沖）可表示為

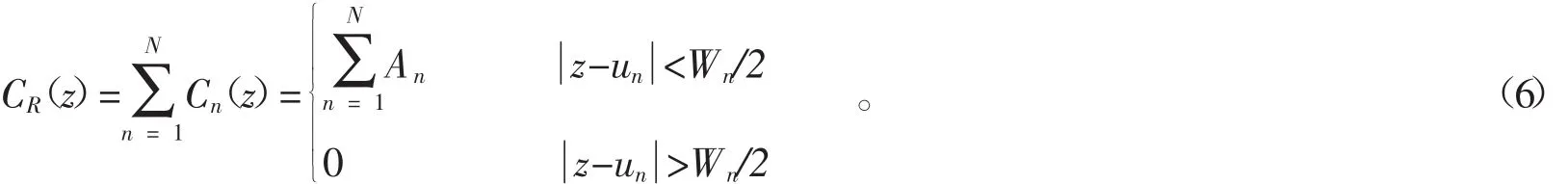
可見這些微彎的曲率脈沖為矩形型。在（4）式中下角標字母R表示矩形型，C（nz）表示第n個微彎的曲率函數，un為第n個隨機微彎在z軸上的位置。An為其曲率脈沖峰值，Wn為其曲率脈沖寬度。

1.2.2.2 功率譜密度 由（4）式可求得其功率譜密度ζ（″△β）

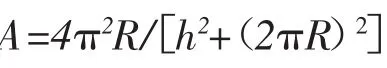
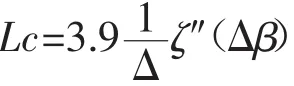
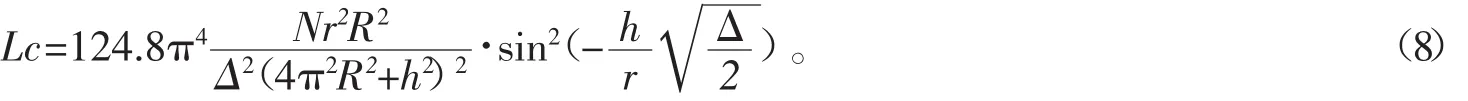
同樣可見，當△、r、R一定時，損耗取決于N、h。

2 數值模擬與分析比較

2.1 數值模擬 假設選用的多模石英梯度光纖其參數為：2r/2R=62.5/125 μm、△=0.01，對（5）式和（8）式進行數值模擬，可分別得圖2和圖3。

1）余弦曲率脈沖模型

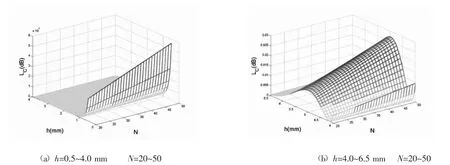
圖2 微彎損耗Lc與h、N間關系

2）矩形曲率脈沖模型

圖3 微彎損耗Lc與h、N間關系

2.2 分析比較

第一，比較（5）式和（8）式可見，兩模型的表達式相似：絞合式光纖的微彎損耗都由三角函數部分和除三角函數部分外的部分之積構成。三角函數部分為調制部分，除三角函數部分外的部分為幅值部分。故微彎損耗按幅值受調制的趨勢變化。這也在圖2和圖3中可見。

第二，兩模型反映的數值關系也基本一致：當△、r、R一定時（亦即選定光纖），絞合式光纖的微彎損耗受螺距h調制，而與微彎數N成正比。見圖2、圖3。

第三，兩模型的幅值大小不同，實際應用中反映為初始損耗不同。這可通過比較圖2中Lc和圖3中Lc的可見。

第四，兩模型的調制部分所決定的極值位置不同。這可通過比較圖2（b）中h=2.5～4.0 mm和圖3（b）中h= 4.0～6.5 mm可見。

總之，兩種模型得到的微彎損耗均按幅值受調制的趨勢變化，這正是光纖微彎損耗已被實驗所驗證的特點〔4〕，故兩種模型都是合理的。只是兩模型初始損耗大小和調制極值位置不同而已，這些需要實驗進一步驗證之，看哪個更合理？但遺憾的是目前沒有很好的測試條件去完成。

3 應用研究

傳感檢測思想：只要將待傳感檢測參數的變化轉化為螺距h變化，進而轉化為光纖微彎損耗的變化即可。目前文獻〔5-6〕來看，已有對應變參數的傳感檢測，即將應變參數的變化轉化為螺距h變化，最終通過檢測光纖的微彎損耗的變化實現對應變的傳感檢測。

基于上述的思想，可尋求更廣闊的應用領域。

4 結束語

本文對絞合式光纖的微彎損耗機制提出了兩種模型，即余弦曲率脈沖模型和矩形曲率脈沖模型，且給出了相應的理論表達式，并通過數值模擬以及理論分析比較等手段論證了兩種模型的合理性。同時，還對絞合式光纖的微彎損耗的傳感檢測應用方面做了探討。

〔1〕葉培大.光纖理論〔M〕.上海：知識出版社，1985：78-119.

〔2〕葉培大，吳彝尊.光波導技術基本理論〔M〕.北京：人民郵電出版社，1981：315.

〔3〕茶國智，姜向東，王少敏.一種監測管道形變的于光纖自纏繞式微彎傳感器〔J〕.計量技術，2002，15（1）：34-37.

〔4〕Lagakos N.Microbend fiberoptic senso〔rJ〕.Applied Optics,1987,26(11):2171-2180.

〔5〕楊建良，郭照華，查開德.絞合式光纖應變傳感器〔J〕.力學學報，2001，33（2）：284-287.

〔6〕杜彥良，金秀梅，孫寶臣，等.基于普通光纖的螺旋纏繞式準分布光纖傳感器研究〔J〕.工程力學，2004，21（1）：48-51.

Research on Microbend Losses Mechanism and Application ofTwisted OpticalFiber

CHA Guozhi

（College of Engineering，Dali University,Dali,Yunnan 671003,China）

Via research on microbend losses mechanism of twisted optical fiber,this paper presents two novel theories of microbend losses and their respective formula,whose rationality is proved by virtue of theory analysis and numerical simulate.In addition,the application potential of twisted optical fiber is deliberated.

twisted optical fiber;microbend losses mechanism;microbend losses application

TP212.14［文獻標志碼］A［文章編號］1672-2345（2012）04-0035-04

大理學院科研基金項目（2007X43）

2011-06-27

茶國智，副教授，主要從事光電檢測與信息處理技術研究.

（責任編輯 袁 霞）