一種雙參數指權平均
符云錦
(鳳凰縣兩林學區,湖南鳳凰 416211)
一種雙參數指權平均
符云錦
(鳳凰縣兩林學區,湖南鳳凰 416211)
首先定義了雙參數指權平均,然后討論其單調性得到了一些結論,并利用這些結論導出一系列平均和不等式。
雙參數平均;單調性;不等式
1 定義
定義1.1 若ai,bi>1(i=1,2,…,n),帶參數s和t的雙參數指權平均定義為

本文探究Za,b(s,t)關于參數s和t的單調性,并發現它本身包含有許多著名的平均,同時利用其單調性導出了許多不等式。
2 引理
引理2.1 若ai,bi>0(i=1,2,…,n),則
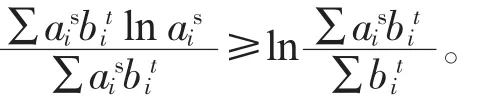
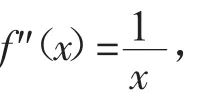
于是當x>0時,f(x)是下凸函數,根據詹生不等式〔1-2〕,得

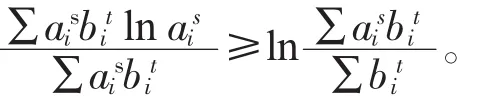
引理2.2〔3〕若ai>0(i=1,2,…,n),則函數
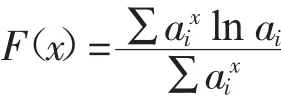
為增函數。
證明:見文獻[3]。
3 主要結論
定理3.1 雙參數指權平均Za,b(s,t)關于參數s是遞增的。
證明:(為了簡便,Za,b(s,t)簡記為Z)
兩端取自然對數并對其求導,得
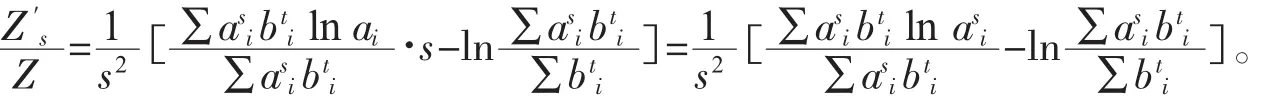
于是,當s≠0時,Za,b(s,t)關于參數s是遞增的。
又由洛必達法則(L’Hospital)[4-5]易知
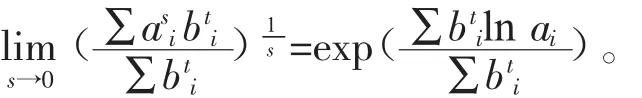
故雙參數指權平均Za,b(s,t)關于參數s是遞增的。
定理3.2 若ai,bi>0(i=1,2,…,n),則
(Ⅰ)當0<ai<1,0<bi<1或ai>1,bi>1或s=0時,Z關于參數t遞增;
(Ⅱ)當0<ai<1,bi>1或ai>1,0<bi<1且s≠0時,Z關于參數t遞減;
(Ⅲ)當bi=1時,Z關于參數t不變。
證明:當s=0時,由引理2.2可知,Z關于參數t遞增;
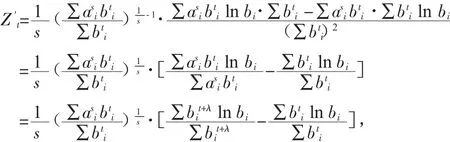
當bi≠1時,判定λ的符號如下:
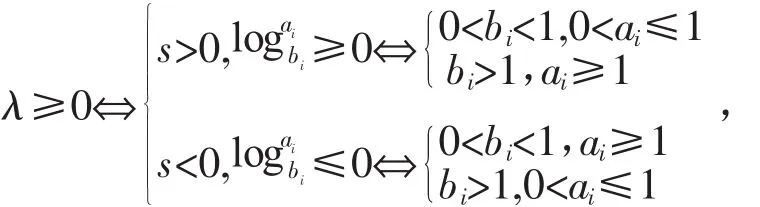
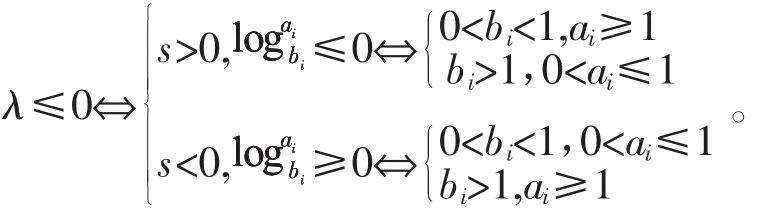
由引理2.2知,若s≠0時,則當λ與s同號時,Z't≥0;當λ與s異號時,Z't≤0,即定理中(Ⅰ)、(Ⅱ)成立。
當bi=1時,雙參數指權平均變為冪平均,即:
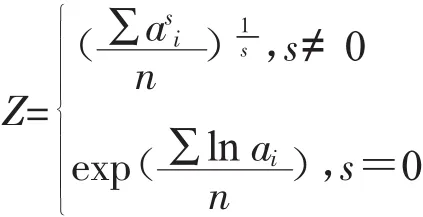
與t無關,即(Ⅲ)成立。
綜上所述,定理3.2得證。
定理3.3 若ai=bi(i=1,2,…,n)時,則Z關于參數s,t均遞增。
證明:由ai=bi,則
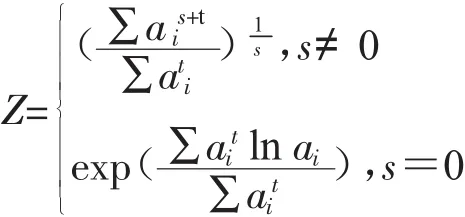
為一種雙參數平均[3],具體證明見文獻[3]。
定理3.4 若s1≤s2,則Za,b(s1,t)≤Za,b(s2,t)。
證明:根據定理3.2可知Za,b(s1,t)≤Za,b(s2,t)。
4 應用
4.1 應用雙參數指權平均導出許多著名平均
(1)當ai=bi時,可以引出許多著名的平均,見文獻[3]。
(2)令t=1,則可得到加權冪平均[6-13],即H?lder’s平均:
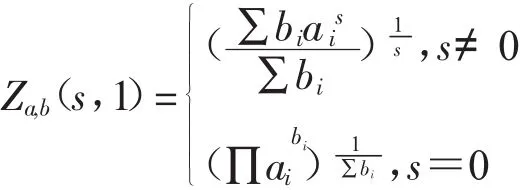
特別的,當bi=1(i=1,2,…,n)時,Za,b(s,1)為冪平均[14]。
4.2 應用雙參數指權平均的性質導出新的不等式
(1)若ai,bi>0時,由定理3.1可得
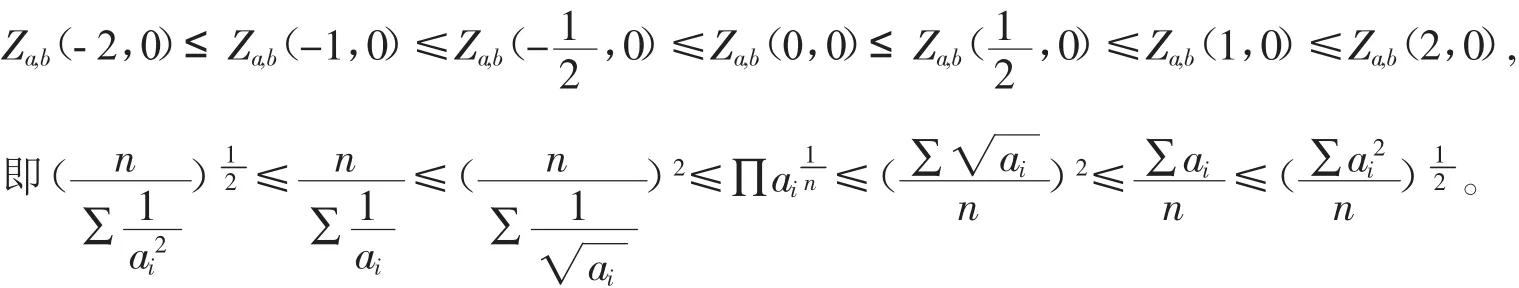
(2)若0<ai<1,0<bi<1,時,由定理3.2可得
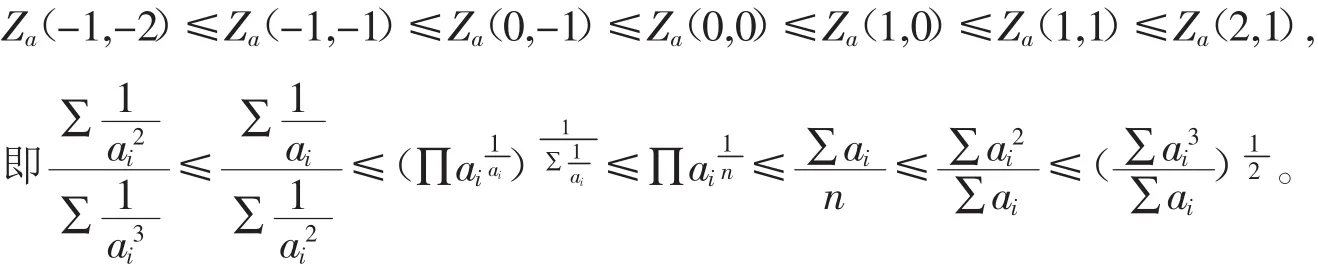
(3)若ai>1,0<bi<1,且s≠0時,由定理3.2可得
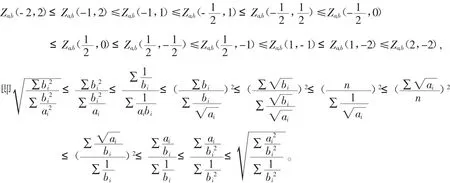
根據本文的結果,還可以導出許多不等式,這里不再贅述。
〔1〕劉玉璉.數學分析講義〔M〕.3版.北京:高等教育出版社,2007.
〔2〕楊學枝.數學奧林匹克不等式研究〔M〕.哈爾濱:哈爾濱工業大學出版社,2009:71.
〔3〕陽凌云,鄭光輝.一種雙參數平均及其應用〔J〕.數學的實踐與認識,2007,37(3):98-103.
〔4〕常庚哲,史濟懷.數學分析教程〔M〕.北京:高等教育出版社,2003:176-177.
〔5〕陳朝暉.利用洛必達法則求二元函數的極限〔J〕.內江科技,2010(6):86.
〔6〕〔英〕哈代,〔英〕利特爾伍德,〔美〕波利亞.不等式〔M〕.2版.越民義,譯.北京:科學出版社,2008:17-19.
〔7〕張曉明,褚玉明.解析不等式新論〔M〕.哈爾濱:哈爾濱工業大學出版社,2009:2.
〔8〕張潔.加權冪平均函數的性質和應用〔J〕.貴州教育學院學報,2007,18(4):30-31.
〔9〕陳遠蘭.關于一般冪平均不等式的構成函數的單調性〔J〕.溫州大學學報:自然科學版,2007,28(4):8-13.
〔10〕畢燕麗.加權冪平均函數的單調性及其應用〔J〕.曲阜師范大學學報:自然科學版,2008,34(2):30-32.
〔11〕洪勇.冪平均不等式的改進及在凸性模估計中的應用〔J〕.科學技術與工程,2006,6(9):1171-1175.
〔12〕曹斌,馬燕,孫艷.關于洛必達法則求函數極限的分析與研究〔J〕.淮海工學院學報:自然科學版,2011,20(1):3-6.
〔13〕杜小琴,姜健飛.在序A4≥(A2B2A2)2/3下的α冪平均函數的單調性〔J〕.東華大學學報:自然科學版,2009,35(2):241-244.
〔14〕匡繼昌.常用不等式〔M〕.2版.長沙:湖南教育出版社,1993:49.
A Two-parameter Defining Weighted Average
FU Yunjin
(Lianglin School District of Fenghuang,Fenghuang,Hunan 416211,China)
This article refers to two-parameter defining the weighted average,and then discusses its monotonicity.Finally some conclusions are summarized,which are used to derive many averages and inequalities.
two-parameter mean;monotony;inequality
O178[文獻標志碼]A[文章編號]1672-2345(2012)04-0001-04
2011-04-21
2011-05-08
符云錦,主要從事初等數學、分析學及其應用、微分方程、教育理論及其應用研究.
(責任編輯 袁 霞)

