幾何、調和平均組合的最佳廣義對數平均界＊

張 帆， 錢偉茂

(1.湖州職業技術學院，浙江湖州 313000;2.湖州廣播電視大學，浙江湖州 313000)

幾何、調和平均組合的最佳廣義對數平均界＊

張 帆1， 錢偉茂2

(1.湖州職業技術學院，浙江湖州 313000;2.湖州廣播電視大學，浙江湖州 313000)

應用初等微分學知識，對幾何平均、調和平均的幾何組合與廣義對數平均進行了比較，解決了如下問題：對于 α∈(0，1)，使雙向不等式 Lp(a，b)≤Gα(a，b)H1－α(a，b)≤Lq(a，b)對所有的 a，b ＞0 成立的最大 p 和最小q分別是多少?

不等式;廣義對數平均;幾何平均;調和平均

對固定的a，b＞0和a≠b，Lp(a，b)關于p∈R是連續和嚴格遞增的.特別地，文獻［1-9］從廣義對數平均Lp(a，b)中發現了許多著名的不等式.廣義對數平均甚至在經濟學、物理學、氣象學中也有應用［10-12］.若記2個正數a，b的算術平均、幾何平均、指數平均、對數平均和調和平均分別為A(a，b)=則有著名的不等式

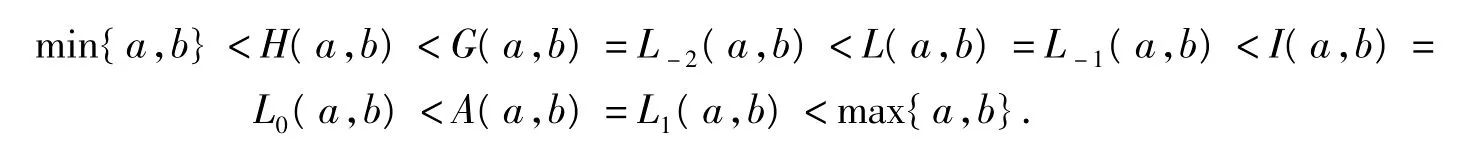
文獻［13-15］得到了如下不等式：

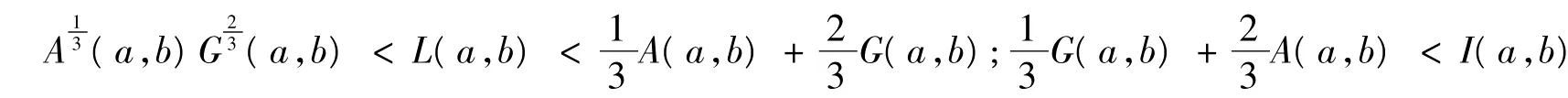
對所有 a，b＞0，a≠b成立.

1986 年，Alzer證明了如下不等式［16］：

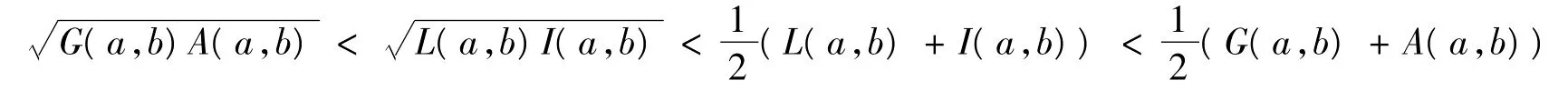
對所有 a，b＞0，a≠b成立.

下面2個結論由Alzer等［17］給出：

定理1［17］不等式

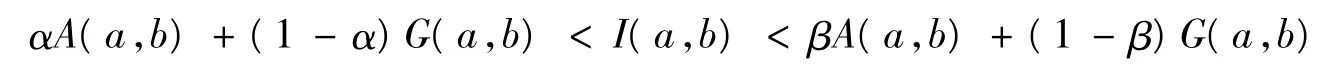
定理 2［17］設 a，b 是實數且 a≠b.若0 ＜a，b ＜e，則

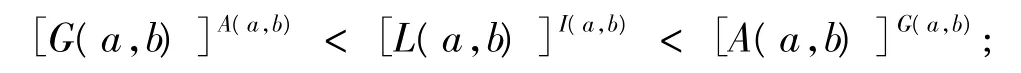
若 a，b≥e，則

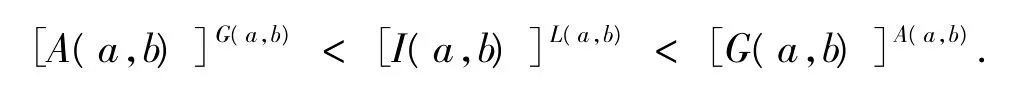
本文的目的是解決如下問題：對于α∈(0，1)，使雙向不等式

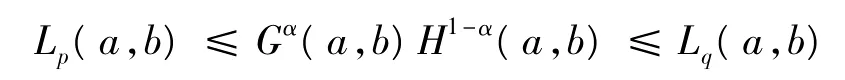
對所有a，b＞0成立的最大p和最小q分別是多少?

1 引理

引理1當t＞1時，設f(t)則

證明 由f(t)的定義得：

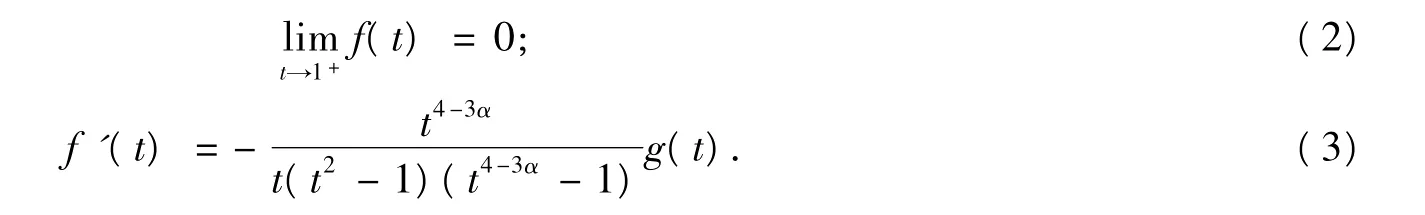
式(3)中：

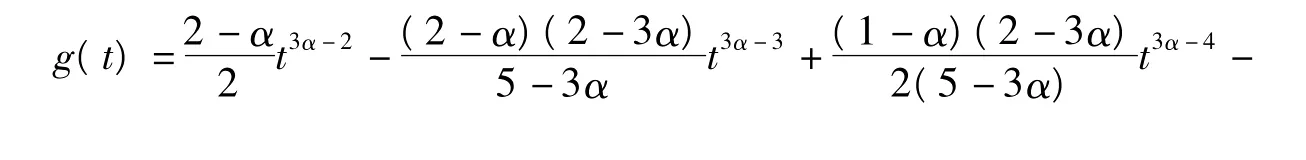
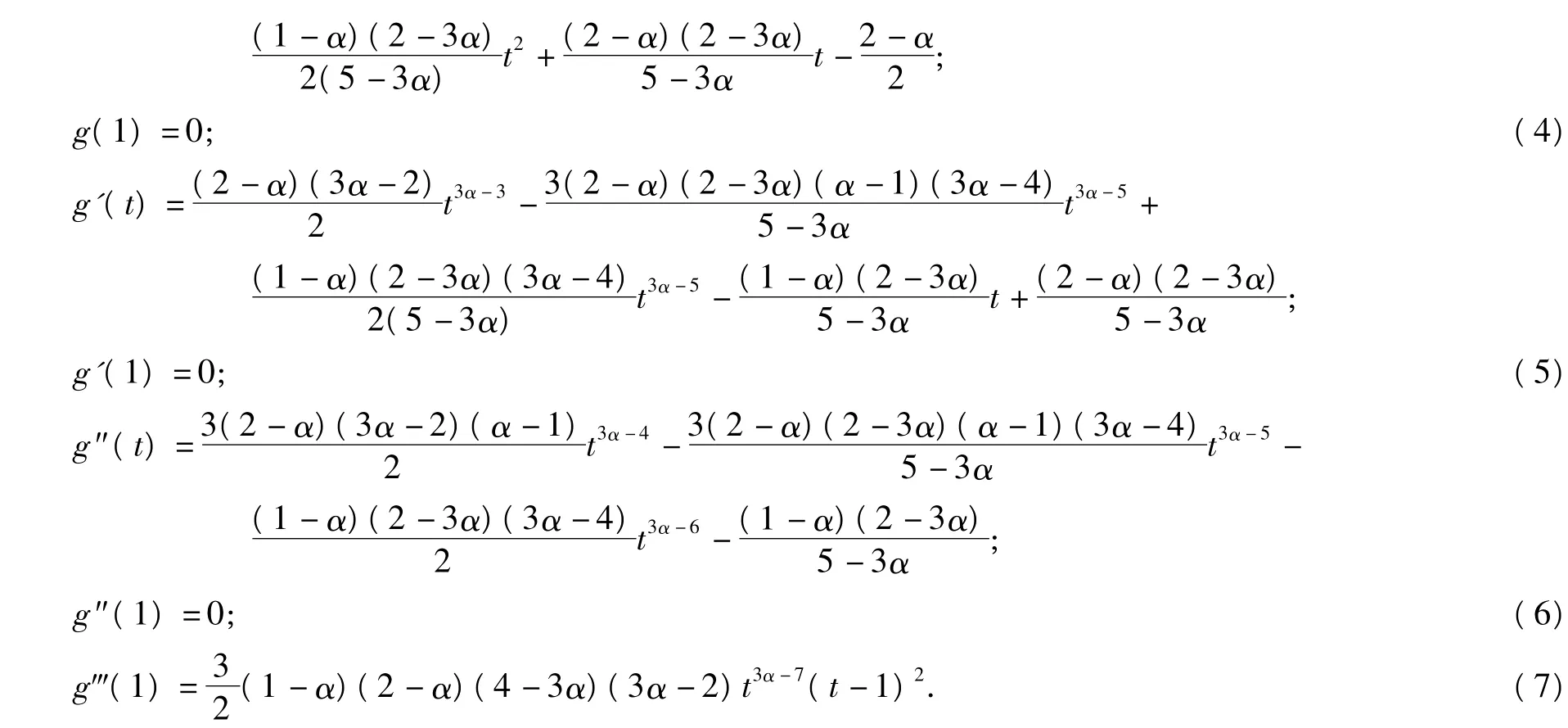
由式(2)～式(6)和式(8)可知，當t＞1時，f(t)＞0.

由式(2)～式(6)和式(9)可知，當t＞1時，f(t)＜0.引理1證畢.

引理2當t＞1時，設h(t)=則

證明 由h(t)的定義得：

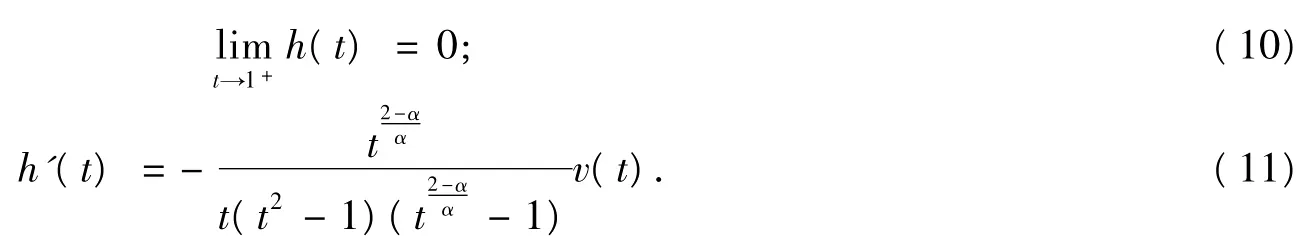
式(11)中：

由式(10)～式(13)及式(15)知，當t＞1時，h(t)＜0.

由式(10)～式(13)及式(16)知，當t＞1時，h(t)＞0.

2 主要結果

定理3若 α∈(0，1)，則對所有 a，b＞0，有：

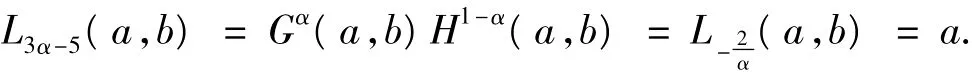
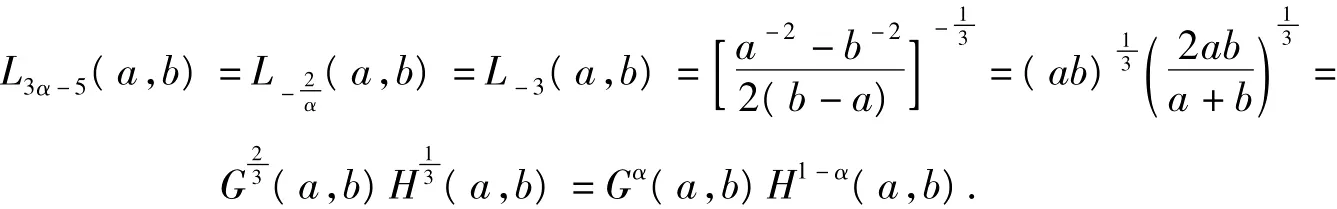
2)若 a=b，則由式(1)得，對?α∈(0，1)，

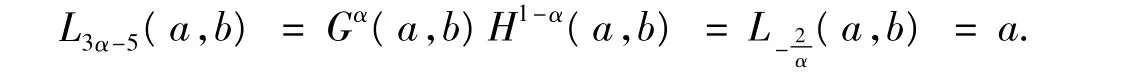
由引理1得：

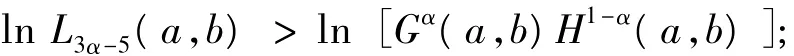
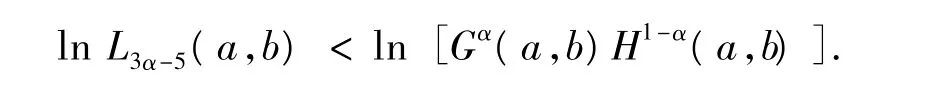
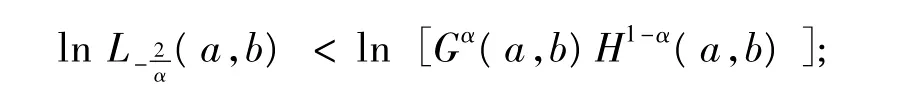
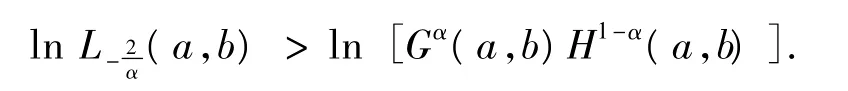
情形1α∈對?ε∈(0，1)，?x∈(0，1)，由式(1)得

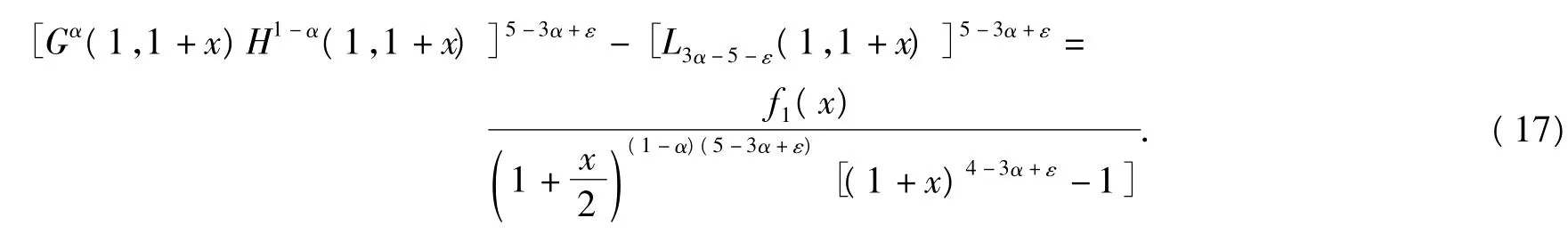
式(17)中，

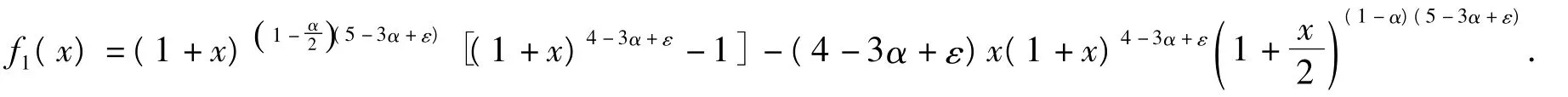
設x→0，利用泰勒展開式得

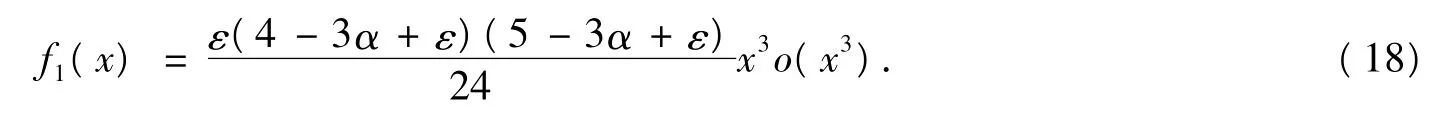
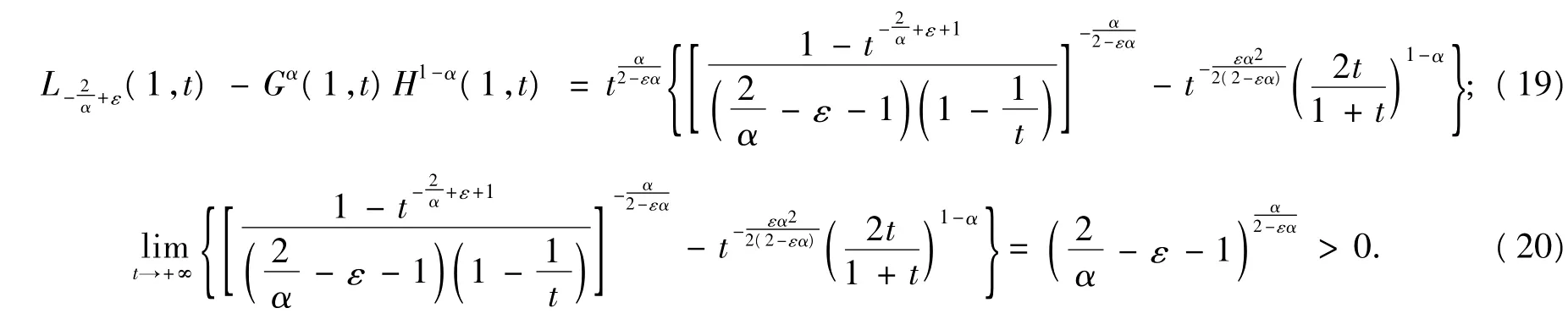
情形2α∈對于?ε∈(0，4 －3α)，?x∈(0，1)，由式(1)有

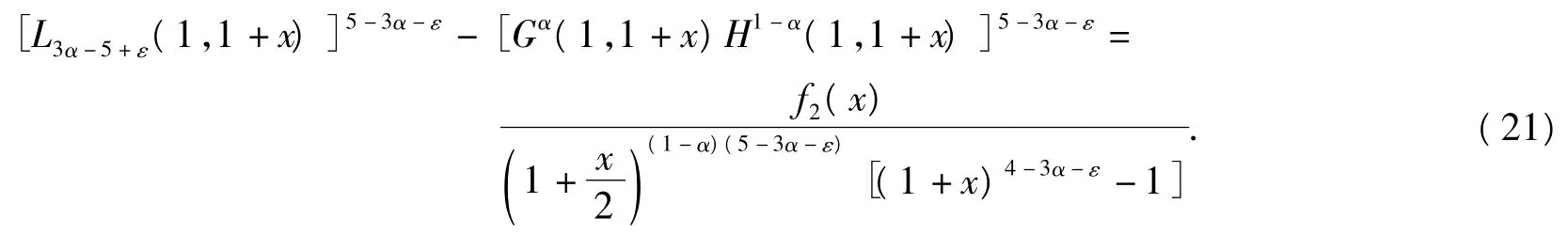
式(21)中，

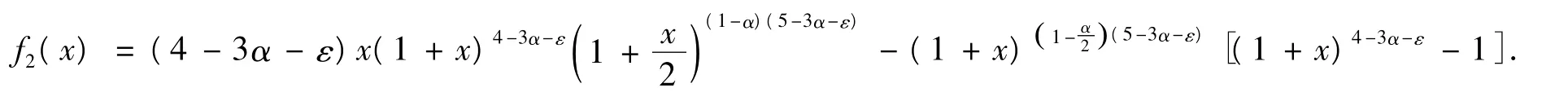
設x→0，利用泰勒展開式，有

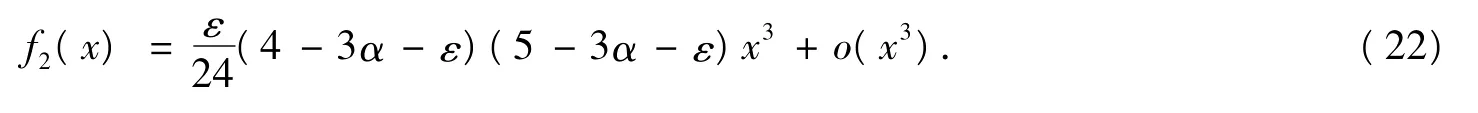
另一方面，對于?ε＞0，有：

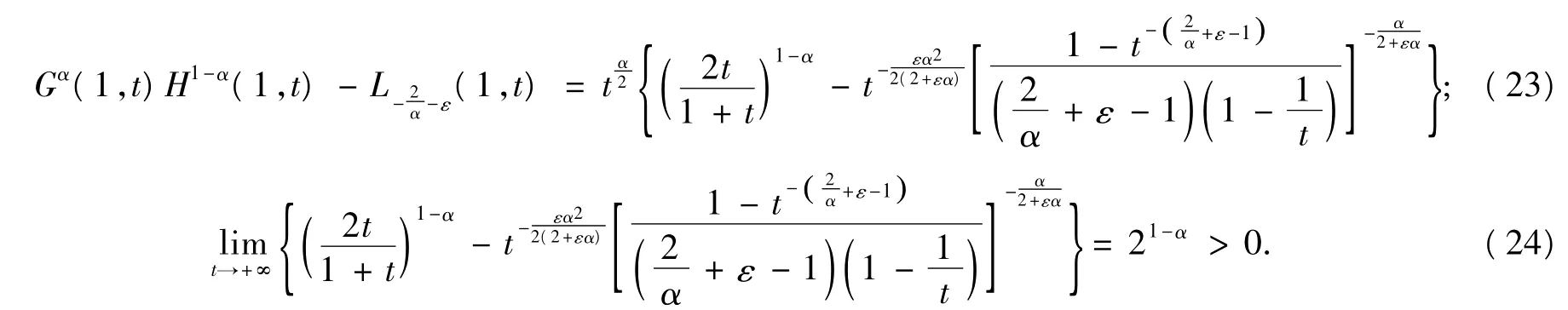
［1］Stolarsky K B.The power and generalized logarithmic means［J］.Amer Math Monthly，1980，87(7)：545-548.

［2］Pearce C E M，Pecaric J.Some theorems of Jensen type for generalized logarithmic means［J］.Rev Roumaine Math Pures Appl，1995，40(9/10)：789-795.

［3］Mond B，Pearce C E M，Pecaric J.The logarithmic mean is a mean［J］.Math Commun，1997，2(1)：35-39.

［4］Chen Chaoping，Qi Feng.Monotonicity properties for generalized logarithmic means［J］.Aust J Math Anal Appl，2004，1(2)：2-4.

［5］Abuhany A A K，Salem S R，Salman I M.On steffensen's integral inequality with applications［J］.J Rajasthan Acad Phys Sci，2006，5(1)：1-12.

［6］Qi Feng，Chen Shouxin，Chen Chaoping.Monotonicity of ratio between the generalized logarithmic means［J］.Math Inequal Appl，2007，10(3)：559-564.

［7］Shi Huanshi.Schur-convex functions related to Hadamard-type inequalities［J］.J Math Inequal，2007，1(1)：127-136.

［8］Chen Chaoping.The monotonicity of the ratio between generalized logarithmic means［J］.J Math Anal Appl，2008，345(1)：86-89 .

［9］Qi Feng，Li Xiaoai，Chen Shouxin.Refinements，extensions and generalizations of the second Kershaw's double inequality［J］.Math Inequal Appl，2008，11(3)：457-465.

［10］Pittenger A O.The logarithmic mean in n variables［J］.Amer Math Monthly，1985，92(2)：99-104.

［11］Kahlig P，Matkowski J.Functional equations involving the logarithmic mean［J］Z Angew Math Mech，1996，76(7)：385-390.

［12］Polya G，Szego G.Isoperimetric inequalities in mathematical physics［M］.Princeton：Princeton University Press，1951.

［13］Leach E B，Sholander M C.Extended mean values II［J］.J Math Anal Appl，1983，92(1)：207-223.

［14］Sandor J.A note on some inequalities for means［J］.Arch Math：Basel，1991，56(5)：471-473.

［15］Carlson B C.The logarithmic mean［J］.Amer Math Monthly，1972，79：615-618.

［16］Alzer H.Ungleichungen für mittelwerte［J］.Arch Math：Basel，1986，47(5)：422-426.

［17］Alzer H，Qiu Songliang.Inequalities for means in two variables［J］.Arch Math：Basel，2003，80(2)：201-215.

Optimal generalized logarithmic mean bounds for the combination of geometric and harmonic means

ZHANG Fan1，QIAN Weimao2

(1.Huzhou Vocational＆ Technical College，Huzhou Zhejiang 313000，China;2.Huzhou Broadcast and TV University，Huzhou Zhejiang 313000，China)

It was compared the generalized logarithmic mean with the geometric combination of geometric and harmonic means by the elementary differential calculus.It was discussed for α∈(0，1)，the greatest value p and the least value q，such that the inequality Lp(a，b) ≤Gα(a，b)H1－α(a，b) ≤Lq(a，b)held for all a，b＞0.

inequality;generalized logarithmic mean;geometric mean;harmonic mean

O178

A

0 引言

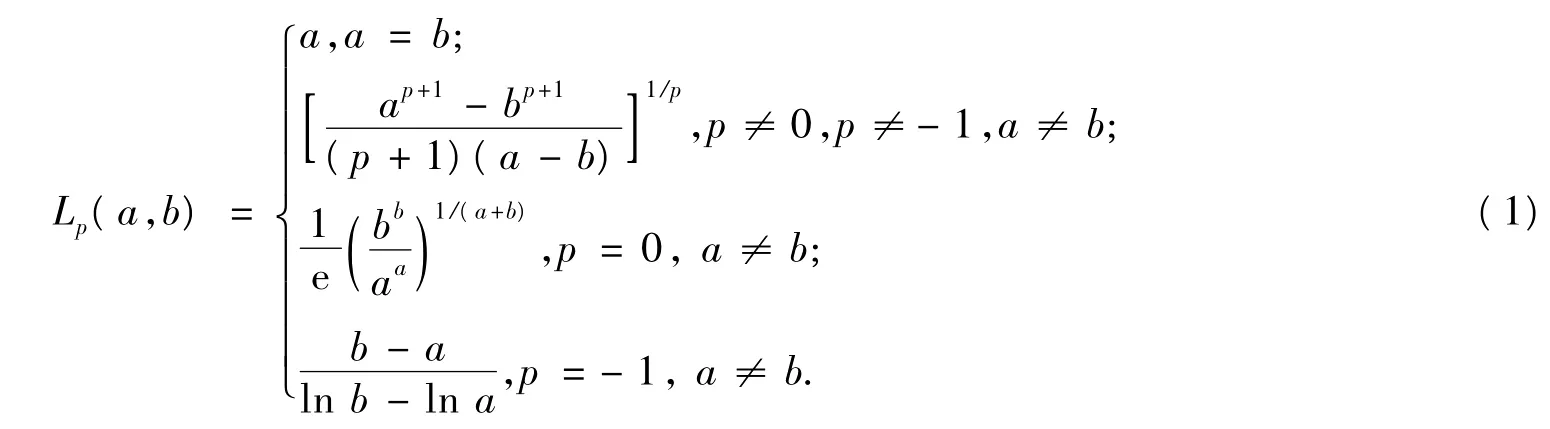
2012-04-27

浙江廣播電視大學2009年度科學研究課題(XKT09G21);湖州市自然科學基金資助項目(2012C50008)

張 帆(1977－)，男，浙江湖州人，講師.研究方向：不等式理論及應用.

1001-5051(2012)03-0252-06

(責任編輯 陶立方)

對于p∈R，關于2個正數a，b的廣義對數平均定義為