漸近非擴張型映像的黏性三步迭代序列強收斂性＊

董家帥， 王元恒， 羅紅平

(浙江師范大學數理與信息工程學院，浙江金華 321004)

漸近非擴張型映像的黏性三步迭代序列強收斂性＊

董家帥， 王元恒， 羅紅平

(浙江師范大學數理與信息工程學院，浙江金華 321004)

在一致凸Banach空間中，研究了漸近非擴張映像不動點的黏性三步迭代法，證明了在一定條件下該迭代序列強收斂于T的不動點，從而改進和推廣了近代相關的一些結果.

漸近非擴張映像;不動點;三步迭代序列;黏性

1 預備知識

設E是一個實Banach空間，E*是E的對偶空間，J：E→2E*是由下列定義的正規對偶映像：

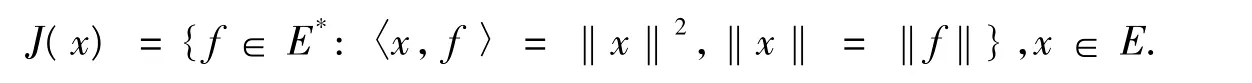
用U={x∈E：‖x‖=1}表示E中的單位球面，稱E為具有Gateaux可微范數，如果極限

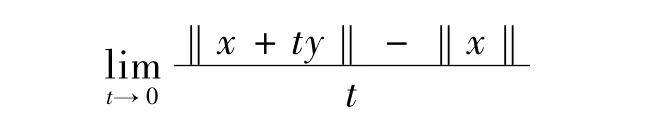
對每一x，y∈U均存在;稱E為具有一致Gateaux可微范數，如果對于每一個y∈U，上述極限是一致存在的.E的光滑模定義為

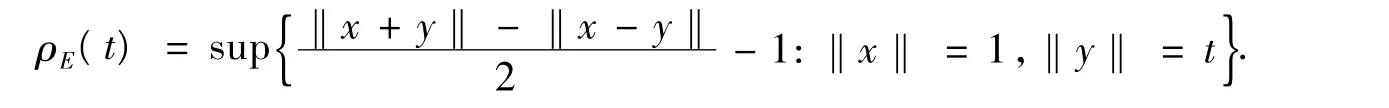
定義1設D是實Banach空間E的非空有界閉凸子集，T和f：D→D為映像，F(T)表示T在D的不動點集.

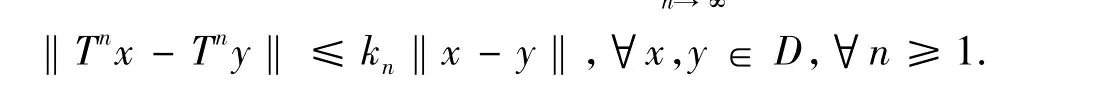
2)稱映像f：C→ C為具有一壓縮常數α∈(0，1)的壓縮映像，如果對任意的x，y∈C，有

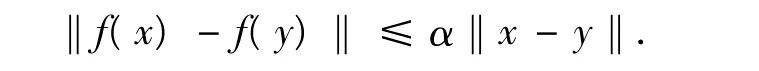
用ΠC表示定義在C上的所有壓縮映像f的集合.為了證明本文的主要結果，還需要下列重要引理：

引理1［6］設{xn}，{yn}是 Banach空間 E中的2個有界序列，{α}是［0，1］中的一實數列，滿足

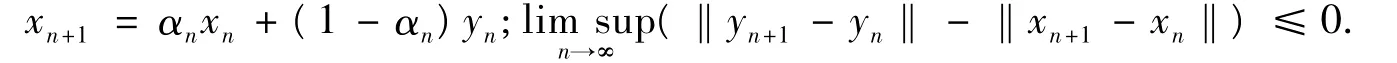
引理2［7］設E是具有一致Gateaux可微范數的實Banach空間，而C是E的非空閉凸子集，令{xn}

n是E的有界序列，且令un是序列{xn}的Banach極限，z∈C，則un‖xn-z‖2‖x-y‖2當且僅

當 un〈y-z，J(xn-z)〉≤0，?y∈C.

引理3［7］設 α 是實數且使得對所有 Banach 極限都有≤α.若≤0，則

引理4［6］設E是實 Banach空間，J：E→2E*是正規對偶映像，則對?x，y∈E及對?j(x+y)∈J(x+y)，有

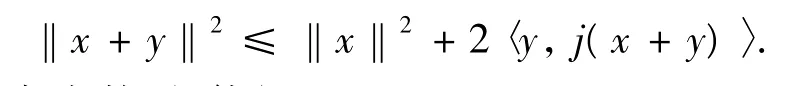
引理5［4］設{αn}是一非負實數列，使得

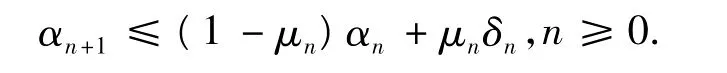
其中：{μn}是(0，1)中的一數列;{δn}是 R 中的一數列，滿足

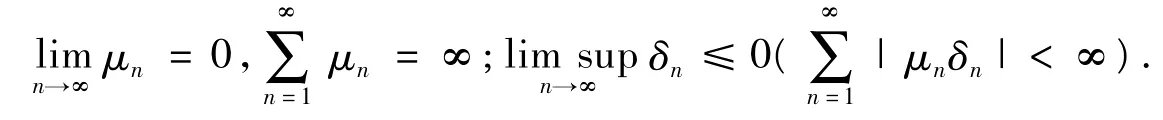
2 主要結果

定理1設E是一致Gateaux可微的Banach空間，C是E非空有界閉子集，T：C→C是具有不動點的漸近非擴張映像且kn≥1，(kn－1) ＜+∞，F(T)≠?，設f：C→C是具有一壓縮常數α(α∈(0，1)) 的壓縮映像且 f∈ ΠC，設{αn}，{βn}，{γn} 是3 個屬于(0，1) 中的實數列，滿足：

則由式(1)定義的迭代序列{xn}強收斂于T的不動點p∈F(T)的充分必要條件是

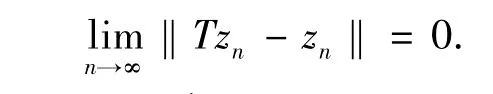
證明 首先證明{xn}有界.取p∈F(T)，則

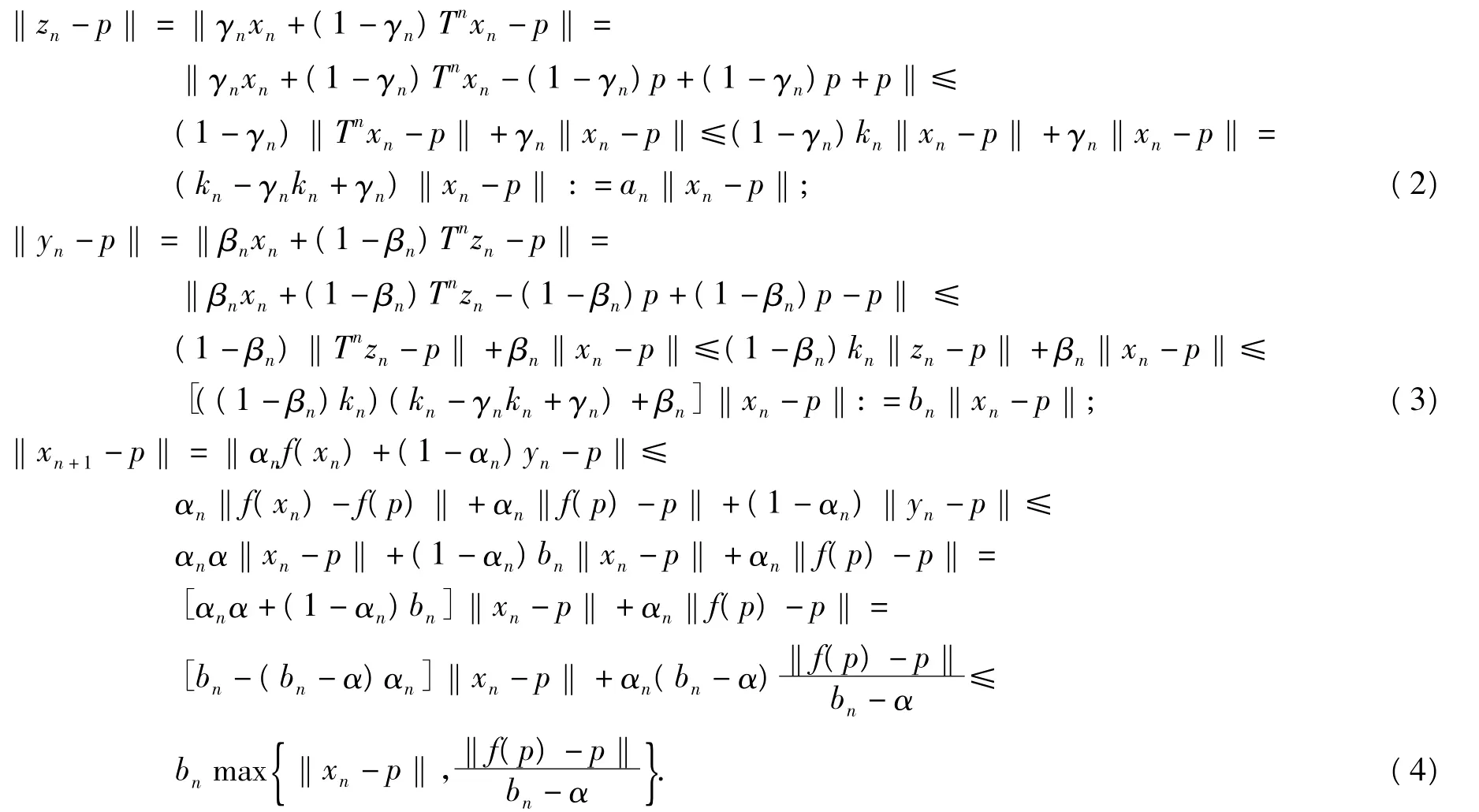
由式(2)～式(4)及歸納法得到

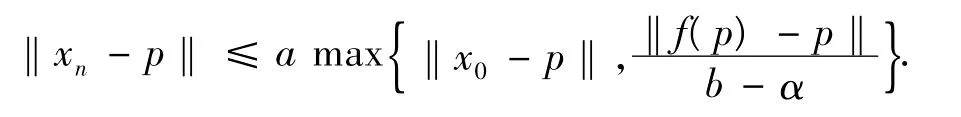
其中：an=(kn-γnkn+γn)，an→1(n→ ∞);bn=［(1-βn)kn］(kn-γnkn+γn)+βn，bn→1(n→ ∞);a=sup{bn}，b=inf{bn}=1.故{xn}是有界的，因此，{yn}，{zn}，{f(xn)}，{Tnxn}也是有界的.

必要性 若xn→p，則由{xn}，{Tnxn}有界和定理1的條件3)、迭代格式(1)中的第1個等式得

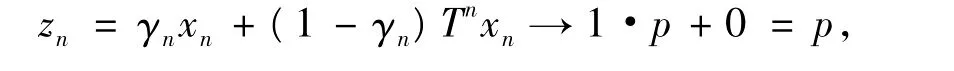
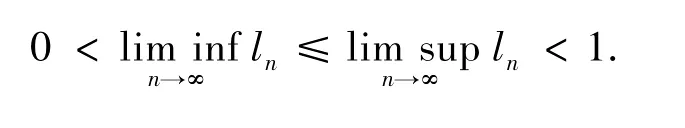
定義xn+1=lnxn+(1-ln)wn，計算得到

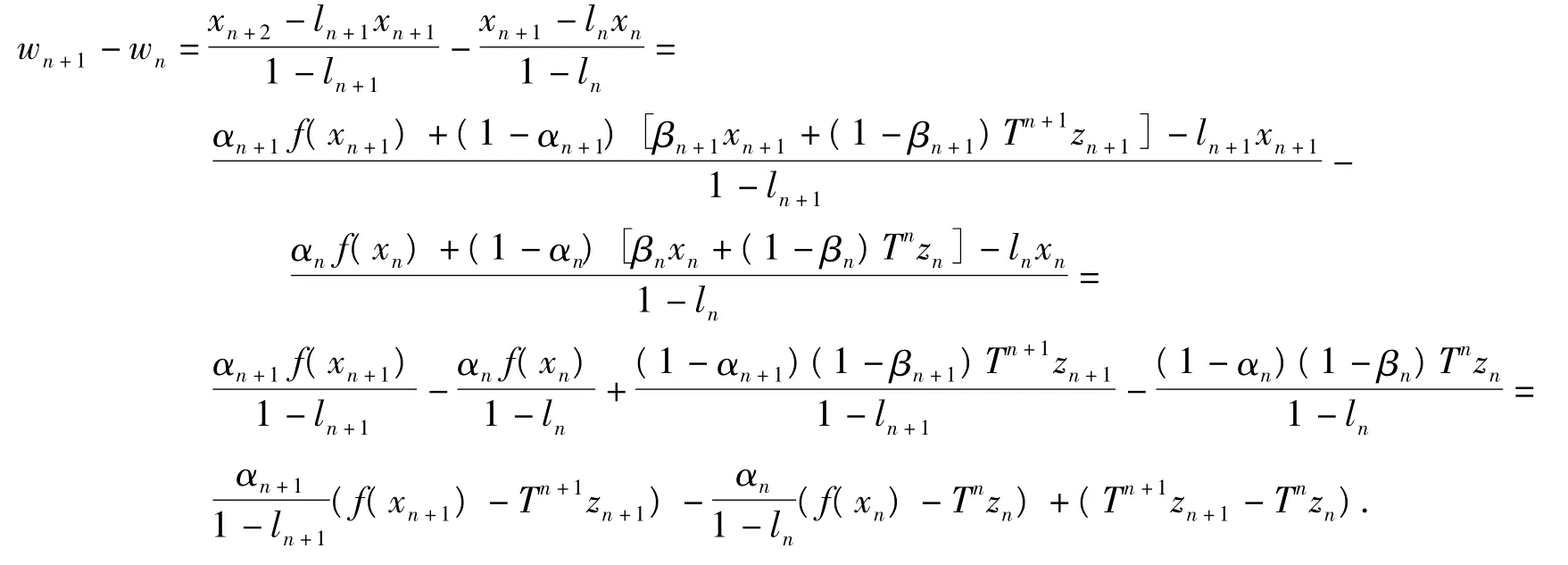
由T是漸近非擴張映像得

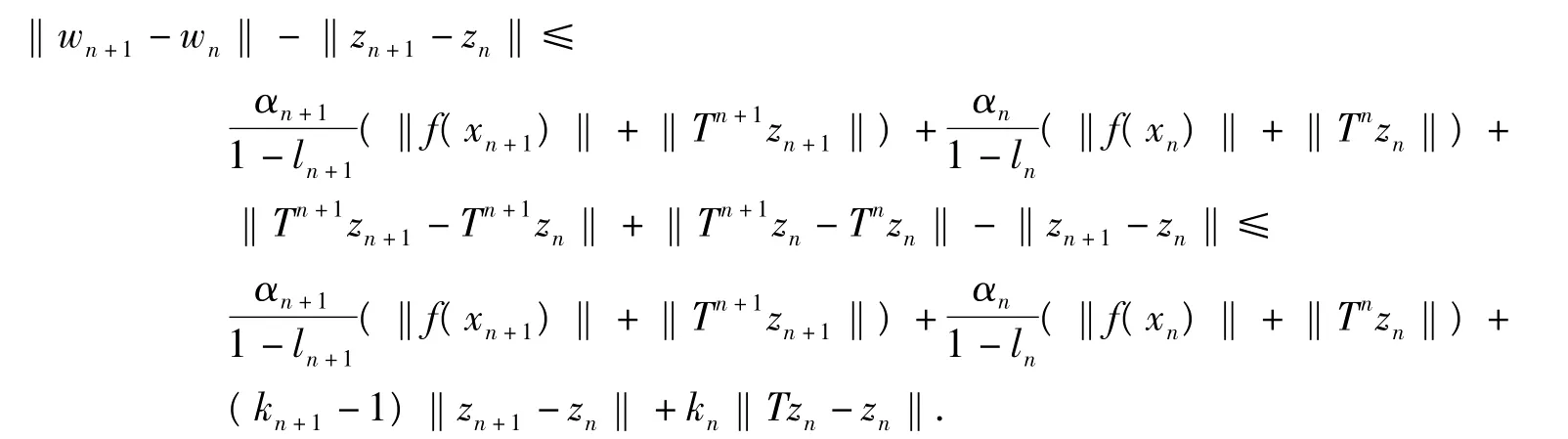
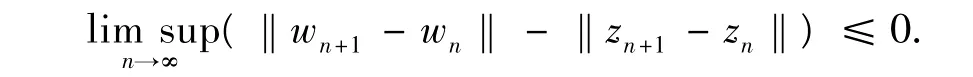
由引理1知

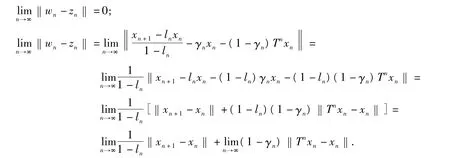
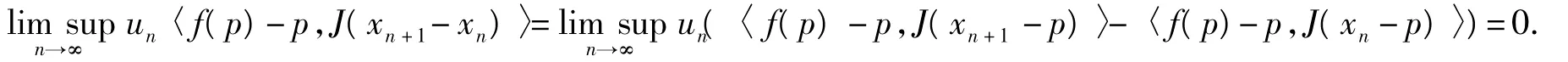
第3步證明xn→p.利用引理4得到

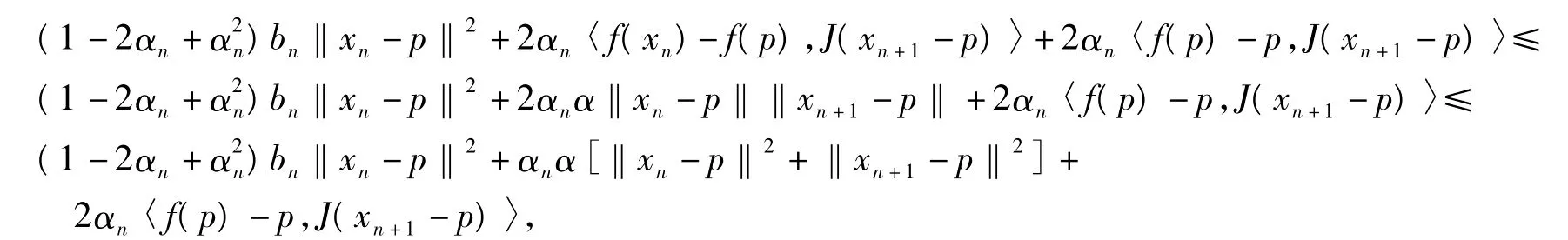
因此，

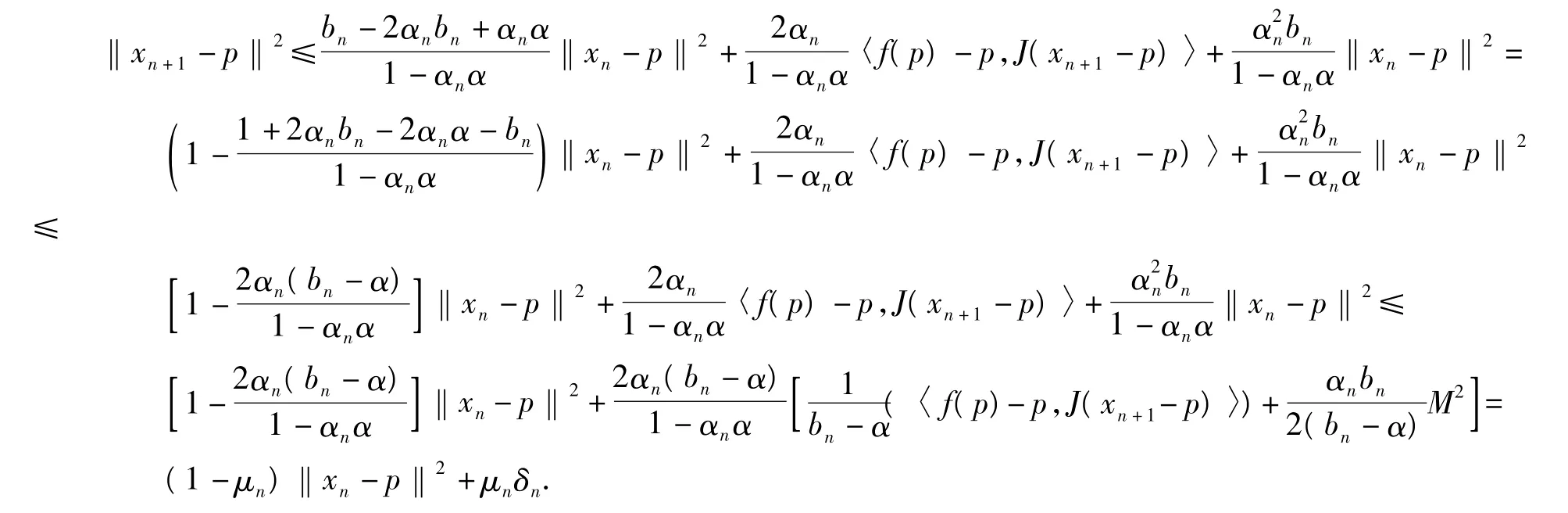
其中：μn=，且存在有 M2＞0，使得‖xn－ p‖2≤M2.同時，容易得出

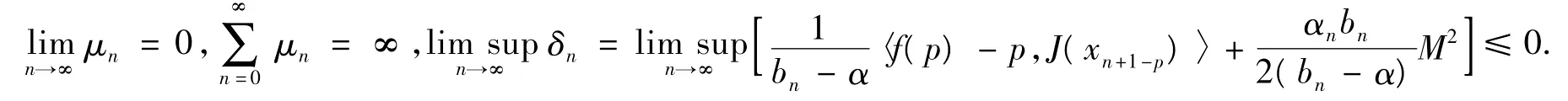
所以由引理5得，當n→∞ 時，xn→p.定理1證畢.

本文證明了漸近非擴張映像的黏性三步迭代序列強收斂性，所得結果改進和推廣了近代一些相關的結果，如文獻［3-5］等.

［1］Xu Benlong，Noor M A.Fixed-point iterations for asymptotically nonexpansive mappings in Banach spaces［J］.J Math Anal Appl，2002，267(2)：444-453.

［2］高改良，周海云.Banach空間中一類映像的三重迭代法［J］.應用泛函分析學報，2011，31(1)：91-94.

［3］Yao Yonghong，Chen Rudong，Yao J C.Strong convergence and certain control conditions for modified Mann iteration［J］.Nonlinear Anal，2008，68(6)：1687-1693.

［4］Qin Xiaolong，Su Yongfu，Shang Meijuan.Strong convergence of the composite Halpern iteration［J］.J Math Anal Appl，2008，339(2)：996-1002.

［5］楊柳，王元恒.修正混合的Halpern三步迭代序列的強收斂性［J］.南陽師范學院學報，2010，9(6)：1-4.

［6］宣渭峰，王元恒.雙復合修正的Ishikawa迭代逼近非擴張映像不動點［J］.浙江師范大學學報：自然科學版，2009，32(4)：401-405.

［7］Song Yisheng.A new sufficient condition for the strong convergence of Halpern type iterations［J］.Appl Math Comput，2008，198(2)：721-728.

Strong convergence of the viscosity three-step iterative sequences for asymptotic noexpansive mappings

DONG Jiashuai， WANG Yuanheng， LUO Hongping

(College of Mathematics，Physics and Information Engineering，Zhejiang Normal University，Jinhua Zhejiang 321004，China)

A new viscosity three-step iterative method for the fixed points of asymptotic noexpansive mappings was given in uniformly convex Banach spaces.A strongly convergent theorem for this kind of iterative sequences was obtained.The results extended some recent results in literatures obtained by other authors.

asymptotic noexpansive mapping;fixed point;three-step iterative sequence;viscosity

O177.91

A

0 引言

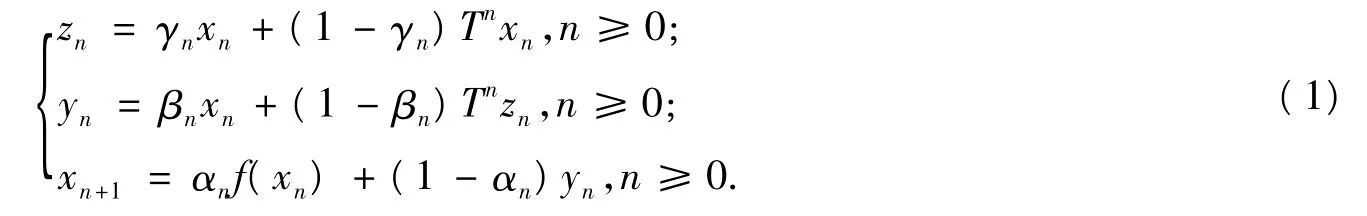
2012-04-11

國家自然科學基金資助項目(11071169);浙江省自然科學基金資助項目(Y6100696)

董家帥(1985-)，男，云南宣威人，碩士研究生.研究方向：非線性泛函分析.

王元恒.E-mial：yhwang@zjnu.cn

1001-5051(2012)03-0241-05

(責任編輯 陶立方)

近年來，Halpern迭代、Mann迭代和Ishikawa迭代方法已向多重的、黏滯的、隱型的等迭代方法發展，并得到了相應的收斂性.例如：文獻［1］提出了三步迭代序列的收斂性;文獻［2］減弱了其三步迭代序列的收斂條件;文獻［3］提出了一個修正的Mann兩步迭代格式;文獻［4］提出了混合的Halpern三步迭代格式;文獻［5］研究了關于非擴張映像的黏性三步迭代序列的強收斂性.本文將進一步研究漸近非擴張映像下的黏性三步迭代序列，并得出相應的結果.對于漸近非擴張映像T，討論如下的黏性三步迭代格式：并證明了在一定條件下序列{xn}的強收斂性.顯然，在式(1)中，令γn=1就變成文獻［3］的兩步修正迭代序列;令f(xn)=μ就類似于文獻［4］的三步混合Halpern迭代序列;當漸近非擴張映像T為非擴張映像時，就變成文獻［5］的黏性三步修正迭代序列.因此，本文推廣了近代相應的一些結果.