機車輪輞超聲探傷信號的數字處理技術

趙 陽，梅勁松，石崢映，屈 薔

（1.南京航空航天大學 自動化學院，南京 210016；2.南京拓控信息科技有限公司，南京 210042）

超聲信號數字處理技術是無損檢測領域的重要研究課題。實際工程中，機車輪輞缺陷形式千變萬化，如剝落、裂紋、磨耗等，其產生的位置各不相同，且噪聲的種類與復雜程度也各異。機車輪輞超聲探傷信號的數字處理主要包括兩個方面：其一，在多種不確定因素和復雜隨機信號的干擾下，將信號處理手段應用于工程實踐中，消除噪聲并提取有效信號，使得系統具有較強的抗干擾能力。其二，利用去噪后的信號，提取回波信號的數字包絡，根據檢波包絡線，判斷機車輪輞有無缺陷和缺陷分布定位，便于后期成像顯示。

筆者采用有限沖激響應濾波器（FIR）和小波變換兩種算法，分別進行數字濾波并對其作對比分析；將去噪后的信號基于三次樣條插值法的數字包絡提取技術進行檢波處理，最終得到了高精度的探傷分析結果。

1 數字濾波對比分析

1.1 噪聲說明

超聲探傷信號中的噪聲主要包括隨機噪聲和相干噪聲。隨機噪聲包括環境噪聲、材料噪聲和電子電路噪聲等，是由各種隨機因素綜合而成的，其頻帶很寬，在探傷過程中隨機出現，將有效信號污染甚至湮沒［1］。圖1是某縱波雙晶探頭的超聲波探傷信號。

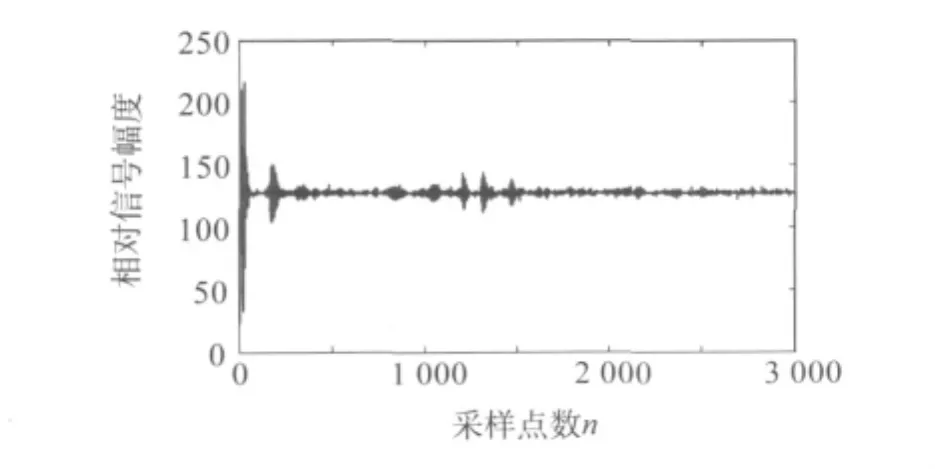
圖1 機車輪輞超聲探傷的原始信號

圖1中的超聲波信號是在工業現場采集到的。除了回波脈沖信號外，信號還包括明顯的高頻噪聲，如果將此信號直接用于判傷，會使判傷結果具有很大誤差。

1.2 濾波理論及算法

1.2.1 FIR數字濾波器

探傷信號的數字通信要求信號在傳輸和處理過程中不能有明顯的相位失真，使用無限沖激響應濾波器（IIR）是很難做到的。有限沖激響應濾波器（FIR）的系統函數只有零點，除原點外沒有極點，所以FIR濾波器總是穩定的，故擬采用FIR數字濾波器［2］。

FIR數字濾波器的基本結構是一個分節的延時線，即把每一節的輸出加權累加，得到濾波器的輸出。數學上表示為：

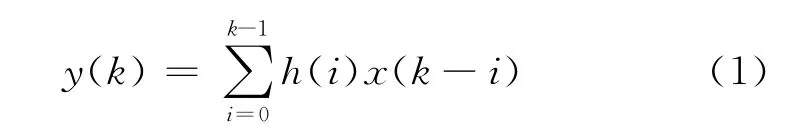
式中k為FIR的抽頭數；h（i）為濾波器的第i級抽頭系數；x（k）為第k時刻的輸入樣本；y（k）為濾波器的輸出樣本。其Z域框圖如圖2所示，其中每個標有z－1的方框代表了一個時鐘周期延時的寄存器單元。

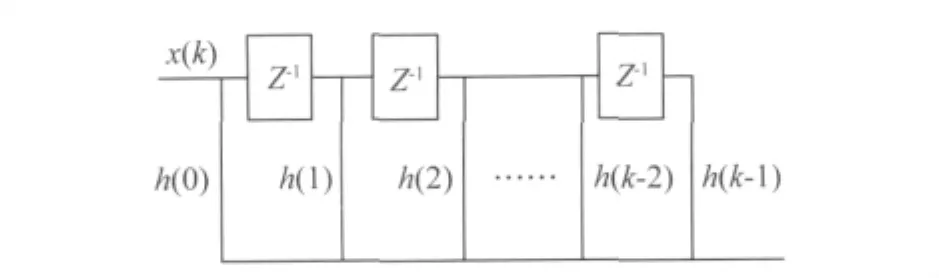
圖2 FIR數字濾波器直接實現形式

基于Matlab平臺，采用窗函數法設計FIR數字濾波器［3］。窗函數法基本思想是用一個有限長度的窗口函數序列ω（k）來截取一個無限長序列hd（k），獲取一個有限長序列h（k）。數學上表示為：

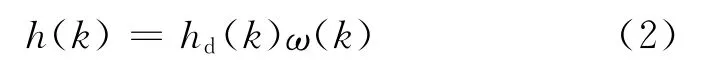
窗函數的設計要滿足兩個條件：① 窗譜主瓣盡可能地窄，以獲得較陡的過渡帶。② 盡量減少窗譜的最大旁瓣的相對幅度，即將能量盡量集中于主瓣，使峰肩和紋波減小，就可增多阻帶的衰減。

1.2.2 小波變換

FIR數字濾波器是屬于經典的去噪方法，它是把有效信號和噪聲在頻域范圍進行分離的方法。這種方法多用于信號頻譜和噪聲頻譜沒有重疊的情況下。而小波變換是一種窗口大小固定，窗口的形狀可變、時間窗和頻率窗都可改變的時頻局部化分析方法。該方法在低頻部分具有較高的頻率分辨率和較低的時間分辨率，在高頻部分具有較高的時間分辨率和較低的頻率分辨率，很適合用來探測在白噪聲等非平穩信號污染下的有效信號中的尖峰成分。

在超聲探傷中取如下含噪的一維信號模型：

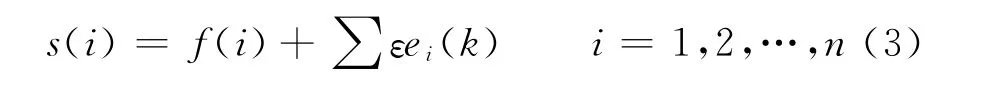
式中s（i）為含噪信號；f（i）為有效信號；∑εei（k）為噪聲疊加；ei為獨立同分布的高斯白噪聲N（0，1）；n為信號長度。取s（i）進行了5層分解，即5層多分辨分析：

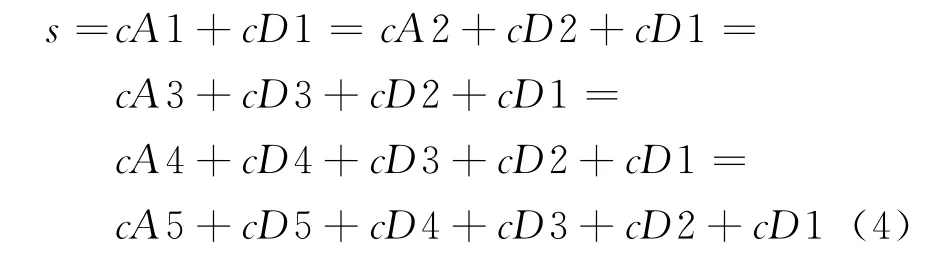
在分解過程中，有效信號通常為低頻信號或平穩信號，產生系數為k層尺度空間的尺度系數，而噪聲信號通常表現為高頻信號，產生系數為k層小波空間的細節系數。上式cAk是各層的尺度系數，cDk是各層的細節系數，k＝1，2，3，4，5。將分解后的小波系數采用門限閾值處理。處理過程中最為重要的就是如何選擇閾值和閾值量化函數。常用的閾值原則有4種：固定閾值原則、無偏似然估計原則、極值閾值原則和啟發式閾值原則。而最常用的閾值量化函數有兩種：硬閾值函數和軟閾值函數。若令t表示閾值，t＞0，則硬閾值信號s的形式為：

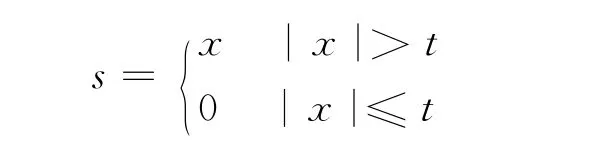
軟閾值信號s的形式為：

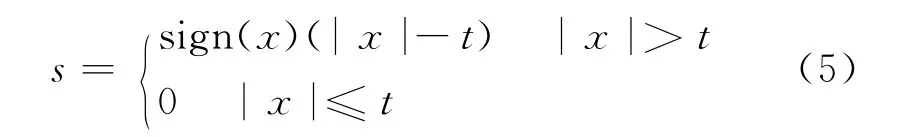
與硬閾值函數相比，軟閾值函數具有更好的數學特性，且處理的結果更為平滑。故采用軟閾值函數對小波系數量化處理。將閾值量化過后的小波系數作逆變換W－1重構信號，即：

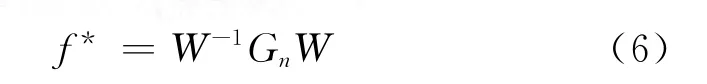
式中GnW 為對小波系數W 作門限閾值處理；f＊為重構后的去噪信號。

1.3 仿真驗證

基于圖1中的超聲探傷信號數據進行試驗。縱波雙晶探頭的中心頻率是2.5MHz，采樣頻率是20MHz，每周期采點數是3000，截止頻率是2.4和2.8MHz。

窗函數中能提供＞50dB的最小阻帶衰減的是海明窗、布萊克曼窗和凱澤窗三種。但海明窗的旁瓣峰值最小，主瓣寬度最窄，可以使濾波器的階數較少，所以選用海明窗來設計FIR數字濾波器。

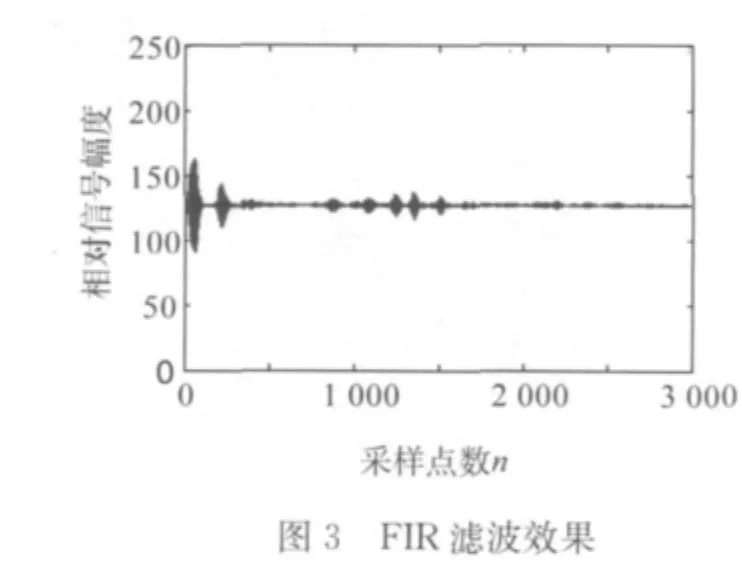
同時運用小波變換進行信號消噪。選擇與超聲探傷的脈沖信號較匹配的Daubechies小波系［4］中的db4小波基，基于Mallat算法進行5層多分辨分析，閾值化處理后重構信號，析出有效信號。將基于FIR的數字濾波器濾波方法與小波變換的方法進行對比，其對比結果如圖3和4所示。

圖3中，使用FIR數字濾波器并沒有達到理想的去噪效果。因為在探傷實際工程中，所遇到的信號大多數是不平穩的，而非平穩信號的時變特性包含了很多方面，只采用單一的手段和窗函數，必然會產生一些不可避免的誤差，可能出現不完整濾波。雖然這嚴格上不算錯誤，但無法有效地反映信號本質的局部特征，故達不到理想的去噪效果。

由圖3和圖4的對比可見，采用同樣原始數據的情況下，基于小波變換的消噪方法與FIR數字濾波器相比，在去噪效果上的有效信號辨識度更高、抗干擾能力更強；小波變換濾波后的脈沖信號表現更加光滑、平整；在回波能量損失上，FIR對始波抑制很嚴重，這種去噪方式是以犧牲清晰度為代價而換取的，故達不到理想的去噪效果。

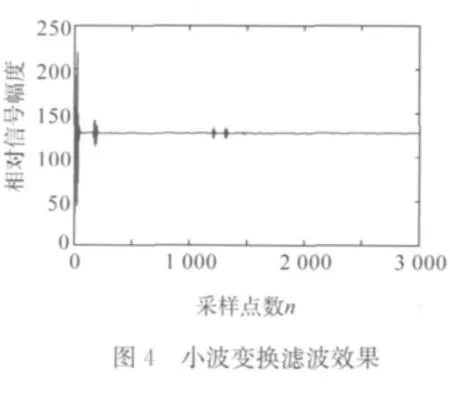
對經小波變換的殘差信號作殘差分析并得到殘差直方圖，如圖5所示。

殘差是指實際觀察值與回歸估計值的差。它的數據量與相對比的數據個數是相等的。分析圖5，直方圖符合近似正態分布，且殘差信號的概率主要集中在幅度為0的鄰域內，可見消噪后的信號與原始信號相差較小，濾波效果較好。

以上超聲探傷信號的研究表明：使用小波變換時，高頻系數的幅值隨著分解層次的增加而迅速地衰減。在此基礎上，選用不同的尺度因子對原始信號進行分析，相當于用一系列帶通濾波器對信號作不同頻段的頻譜分析［5］，故小波變換相比于FIR數字濾波器更適合對超聲探傷信號消噪。

2 信號包絡的檢波分析

小波變換雖能濾除超聲回波信號的大部分噪聲，但是要準確地提取回波，方便技術人員判傷，還需要根據回波信號的包絡來進行分析。筆者將經小波變換后的濾波信號采用樣條插值法來提取信號包絡，以便工程技術人員判傷。

樣條法是用一平滑曲線對各主干點進行擬合的方法。它是通過構造不同階多項式來形成一條把所有主干點連接起來的平滑曲線。一般常常選擇三次曲線（根據三次插值樣條函數所得的曲線）進行擬合。

數學上尋找插值函數是相當復雜的［6］，但Matlab平臺提供了現成的三次樣條插值函數，既簡化了源程序編寫難度，又利用其強大的作圖功能方便地擬合出光滑曲線，為工程應用提供了便利。

將小波變換后的去噪信號作為輸入信號，基于Matlab抽取信號上以5個點為區間的局部極大值點作為各主干點，結合三次樣條插值法對曲線擬合，提取圖4信號的正包絡線如圖6和7所示。

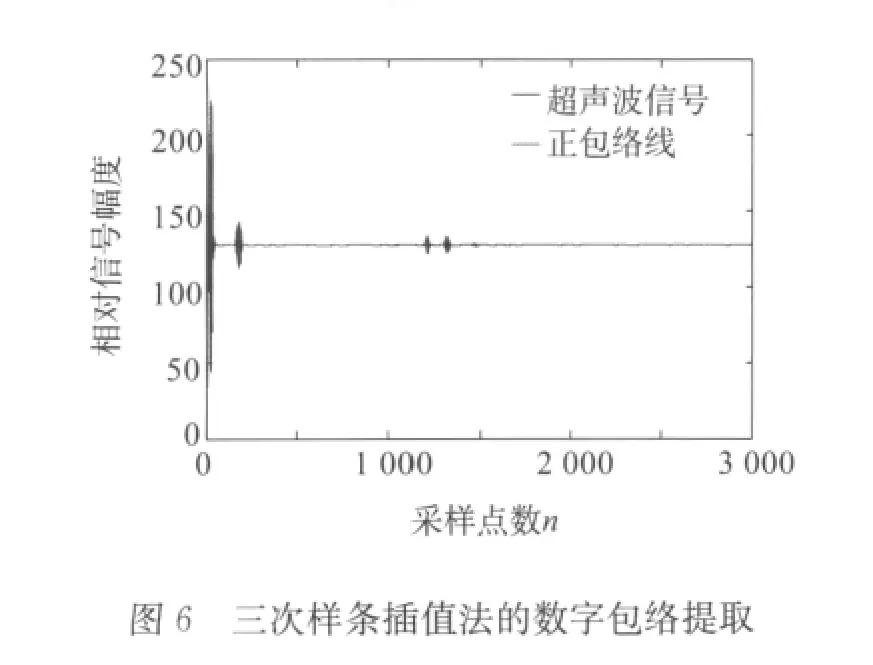
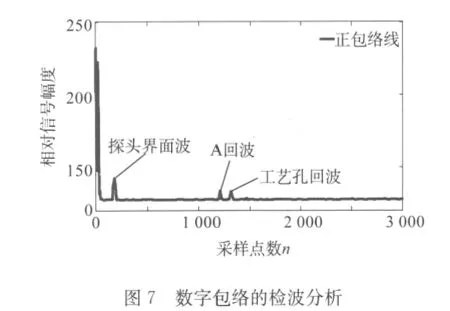
在圖6，7的正檢波分析中，探頭界面波與探頭特性和工藝相關，因探頭而異，可以理解為始波范疇；工藝孔回波是由于超聲波遇到機車整體輪中的應力孔而反射回來的回波信號，其峰值在點n1＝1313處，根據超聲波在機車輪輞中的聲速v＝5920m／s，可以計算出s1＝194.324mm，與應力孔位置相符；A回波產生的可能性比較復雜，主要有兩種原因：缺陷存在或應力孔周圍不平整，其峰值在點n2＝1206處，根據超聲波在機車輪輞中的聲速v＝5920m／s，其位置在s2＝178.488mm處。不管哪種可能，均已經較好地表明文中的數字檢測方法是有效的。

3 結語

對FIR數字濾波器和小波變換的去噪能力作了對比分析。在分析小波去噪后的信號時，提出了三次樣條插值法提取超聲探傷信號的數字包絡，構建了以數字濾波和包絡檢波為核心的超聲探傷信號的數字處理技術。研究表明，鑒于超聲探傷信號中的噪聲具有非平穩性和復雜性的特點，傳統的濾波器已不如小波變換更加適用；選取能夠得到平滑曲線、具有優良數學特征的三次樣條插值法來提取探傷信號的數字包絡曲線是合適的。文中的數字處理技術可用于超聲探傷信號分析，具有辨識度高和抗干擾能力強的特點，在實際工程中具有廣泛的應用前景。

［1］胡天明.超聲探傷［M］.武漢：武漢測繪大學出版社，1996.

［2］何曉麗.高速磁浮列車間隙檢測信號的數字濾波器設計與實現［D］.成都：西南交通大學，2008.

［3］陳亞勇.MATLAB信號處理詳解［M］.北京：人民郵電出版社，2001：163－167.

［4］張廣明.超聲無損檢測中的時頻分析理論及應用研究［D］.西安：西安交通大學，1999.

［5］鄒曉紅.小波分析在超聲回波測量中的應用［J］.傳感器技術，2005，24（7）：78－82.

［6］鞠時光，郭偉剛.實用三次樣條插值函數［J］.小型微型計算機系統，1992，13（9）：20－23.