渦流傳感器檢測(cè)薄板內(nèi)氣孔型缺陷的三維仿真
譚書濤,陳建鈞,潘紅良
(華東理工大學(xué) 機(jī)械與動(dòng)力工程學(xué)院,上海 200237)
渦流檢測(cè)作為五大無損檢測(cè)手段之一,操作簡(jiǎn)單、無需耦合劑、無污染、可在高溫環(huán)境下作業(yè)、快速高效、能實(shí)現(xiàn)自動(dòng)化等優(yōu)點(diǎn),被廣泛應(yīng)用于航空、航天、核能、電力、鋼鐵和石油等行業(yè)。它能可靠準(zhǔn)確地實(shí)現(xiàn)金屬板探傷、管材探傷、結(jié)構(gòu)件疲勞裂紋探傷、材料成分的鑒別、熱處理狀態(tài)的鑒別、測(cè)量金屬薄板的厚度等諸多功能[1]。
渦流檢測(cè)對(duì)缺陷進(jìn)行定量、定性分析時(shí),一般采用當(dāng)量比較法,即根據(jù)國(guó)家制定的探傷標(biāo)準(zhǔn),用同一規(guī)格無缺陷樣品在其上按標(biāo)準(zhǔn)刻制一個(gè)人工缺陷,然后探頭檢測(cè)該樣品并采集信號(hào),該信號(hào)在實(shí)際檢測(cè)中作為標(biāo)準(zhǔn)對(duì)比信號(hào)。通過這種單純的試驗(yàn)方法去獲取數(shù)據(jù),存在著成本高、數(shù)據(jù)少、周期長(zhǎng)等缺點(diǎn)。隨著有限元方法的廣泛應(yīng)用,渦流檢測(cè)的電磁學(xué)仿真很好地彌補(bǔ)了這些缺點(diǎn)。文章采用三維模型仿真了不同大小、不同深度氣孔缺陷的阻抗信號(hào)變化。常規(guī)渦流檢測(cè)是一種表面或近表面的無損檢測(cè)方法,文章模擬的檢測(cè)對(duì)象是2.5mm厚的薄板,通過調(diào)整頻率大小盡量使渦流滲透到薄板下表面。
1 理論原理及數(shù)學(xué)模型
1.1 基本工作原理
渦流檢測(cè)以電磁感應(yīng)原理為理論基礎(chǔ),對(duì)檢測(cè)線圈中通入正弦交變電流,線圈周圍空間將產(chǎn)生交變磁場(chǎng),置于交變磁場(chǎng)中的導(dǎo)電試件會(huì)感應(yīng)出渦流[2]。由楞次定理可知,此渦流又會(huì)產(chǎn)生與線圈磁場(chǎng)方向相反的磁場(chǎng),進(jìn)而會(huì)部分抵消線圈磁場(chǎng),導(dǎo)致檢測(cè)線圈的阻抗發(fā)生變化。保持其他條件不變,若導(dǎo)電試件存在缺陷時(shí),試件中渦流的軌跡及強(qiáng)度發(fā)生變化,使得線圈相對(duì)于無缺陷的阻抗發(fā)生變化。檢測(cè)該變化值便可判斷有無缺陷及缺陷大小。
1.2 數(shù)學(xué)模型
渦流檢測(cè)與其他電磁場(chǎng)問題一樣,都是通過一組麥克斯韋方程組來推導(dǎo)出控制方程。因?yàn)闄z測(cè)線圈的激勵(lì)源為正弦交流電流,控制方程的推導(dǎo)則基于時(shí)諧電磁場(chǎng)麥克斯韋方程組,如下:
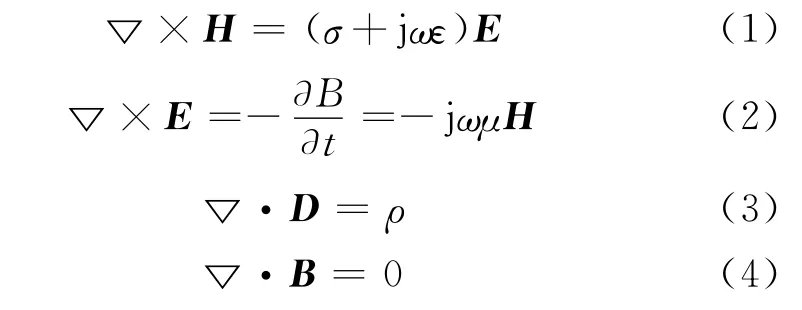
對(duì)于各向同性的線性介質(zhì),還有三個(gè)描述介質(zhì)性質(zhì)的方程,如下:

由磁勢(shì)的旋度等于磁通量的密度,可得如下方程:

把式(5)和(6)代入式(1)方程左邊得:
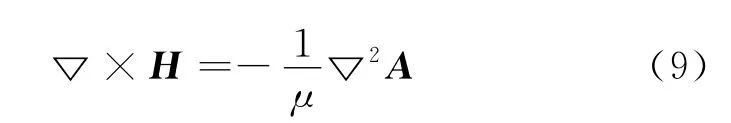
把式(6)代入(2)式可得:

把式(9)和(10)代入式(1)中可得控制方程為:
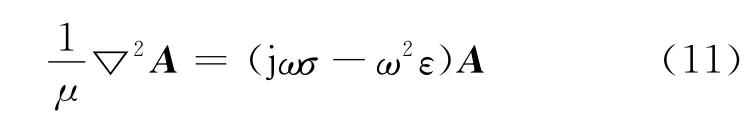
式中μ表示磁導(dǎo)率;A表示磁失勢(shì);ω表示激勵(lì)電流的角頻率;σ表示電導(dǎo)率;ε表示介電常數(shù)。
通過有限元方法求解出式(11)微分方程的解,也就是得到存在渦流效應(yīng)時(shí)的磁失勢(shì)Ae,進(jìn)而將Ae帶入式(12)最右邊的式子,求解出檢測(cè)線圈的阻抗值:
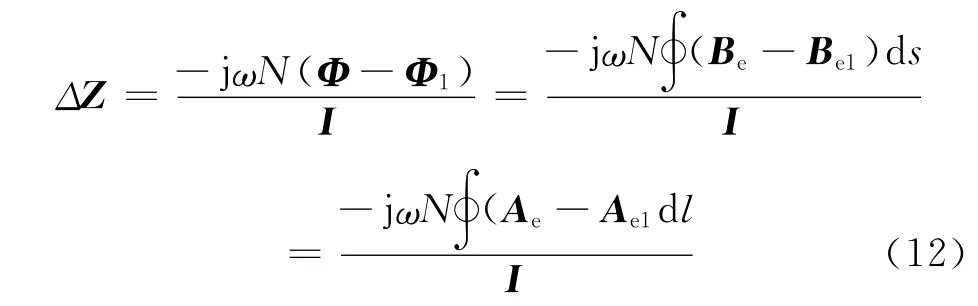
式中ΔZ為線圈阻抗變化值;Ae,Ae1分別為有缺陷和無缺陷時(shí)的磁失勢(shì);I為線圈通入的有效電流值;Be,Be1分別為有缺陷和無缺陷時(shí)的磁場(chǎng)強(qiáng)度;Φ,Φ1分別為每匝線圈有缺陷和無缺陷時(shí)的磁通量值。
2 ANSYS-APDL有限元建模過程
ANSYS軟件是一款大型通用、功能強(qiáng)大和使用方便的有限元分析軟件。它可以進(jìn)行結(jié)構(gòu)、流體、熱、聲學(xué)和電磁學(xué)的計(jì)算,而且還可以進(jìn)行多物理場(chǎng)耦合的計(jì)算。文章是基于電路-磁場(chǎng)耦合模塊,并采用節(jié)點(diǎn)法進(jìn)行時(shí)諧電磁場(chǎng)分析[3]。
2.1 物理模型
圖1為渦流探頭工作時(shí)的二維示意圖。被測(cè)導(dǎo)體的長(zhǎng)寬高為70mm×70mm×2.5mm,氣孔缺陷直徑為φ,其中心離平板上表面的距離為t。被測(cè)導(dǎo)體相對(duì)于線圈而言可以認(rèn)為是無窮大,線圈在缺陷左右兩邊采集到的阻抗變化值以缺陷中心為中心呈近似對(duì)稱分布,當(dāng)線圈到達(dá)缺陷中心位置時(shí),阻抗改變值最大,因此在仿真時(shí)只需計(jì)算線圈位于缺陷中心處的阻抗改變值,就可以反映出缺陷的最大信號(hào)值。
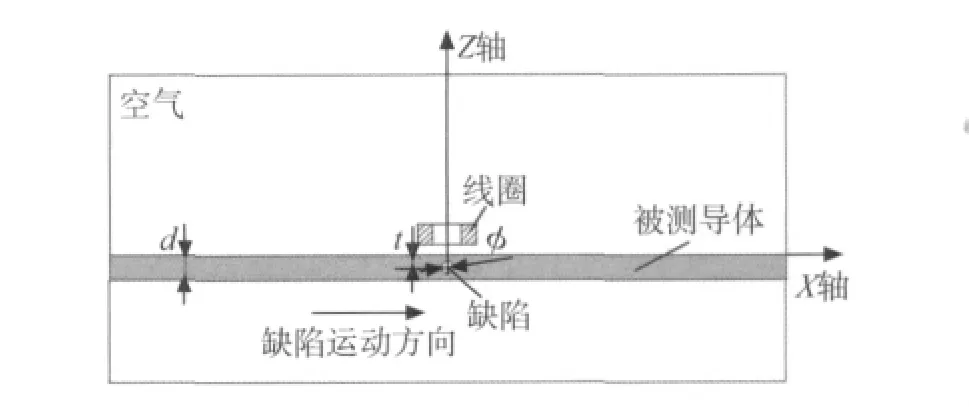
圖1 渦流檢測(cè)內(nèi)部氣孔的二維示意圖
2.2 定義單元類型和材料屬性
在整體模型中,因采用三維節(jié)點(diǎn)法分析,故對(duì)線圈、被測(cè)導(dǎo)體和空氣采用SOLID97實(shí)體單元。然后定義CIRCU124電路單元,建立一個(gè)獨(dú)立電流源,并將此電流源與檢測(cè)線圈耦合,給線圈提供1/140A的電流。被測(cè)導(dǎo)體采用銅材料,其相對(duì)磁導(dǎo)率μγ=1,電導(dǎo)率ρ=1×10e-6(Ω×m)[4]。
2.3 網(wǎng)格劃分
在被測(cè)導(dǎo)體中由于感應(yīng)渦流的存在,網(wǎng)格劃分時(shí)就需要考慮集膚深度的影響,在集膚效應(yīng)顯著的區(qū)域應(yīng)加密網(wǎng)格數(shù)。該區(qū)域主要是線圈下方包圍缺陷的銅板區(qū)域,其X軸和Y軸方向的網(wǎng)格精細(xì)度要求不高,在Z軸方向應(yīng)進(jìn)行精細(xì)剖分[5],故此區(qū)域采用映射網(wǎng)格劃分,在Z軸方向上薄板的網(wǎng)格層數(shù)為7層。上下空氣層采用映射網(wǎng)格劃分,與線圈和被測(cè)導(dǎo)體接觸的空氣區(qū)域采用自由網(wǎng)格劃分。劃分后的線圈和銅板的網(wǎng)格模型如圖2。

圖2 線圈和銅板的網(wǎng)格模型
2.4 定義線圈實(shí)常數(shù)
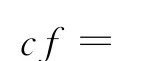
2.5 設(shè)置邊界條件及加載
文章模型屬于第一類邊界條件[7],即令邊界面上所有節(jié)點(diǎn)的磁失勢(shì)AX=AY=AZ=0;對(duì)線圈加載交變電流時(shí),是通過設(shè)置獨(dú)力電流源的實(shí)常數(shù)來添加I=1/140A的電流,以及HARFR命令符來設(shè)置加載電流的頻率。
2.6 求解及后處理
以上步驟完成后,定義分析類型為諧波分析HARMONIC,并選擇稀疏矩陣求解器,執(zhí)行求解;求解結(jié)束后,在通用后處理器POST1中提取實(shí)部和虛部結(jié)果,以命令符Path定義線圈內(nèi)的環(huán)形封閉路徑,F(xiàn)luxv求解出穿過封閉路徑的磁通量,而為了更精確地求解出感應(yīng)電壓,共定義9個(gè)封閉路徑如圖3,取得磁通量的平均值Φ,把Φ代入式(12)求出檢測(cè)線圈的阻抗改變值。
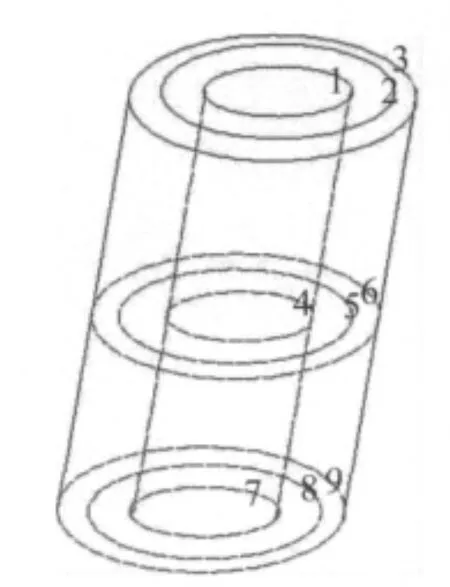
圖3 定義的9個(gè)封閉路徑
3 計(jì)算結(jié)果分析
3.1 最佳激勵(lì)頻率的確定
在渦流檢測(cè)時(shí),渦電流的滲透深度和檢測(cè)靈敏度是一對(duì)矛盾。激勵(lì)頻率過高,由于集膚效應(yīng)的存在,渦電流局限在表面薄層中流動(dòng),缺乏有效的檢測(cè)深度;相反,激勵(lì)頻率過低,會(huì)增加滲透深度,但降低了檢測(cè)靈敏度。因此,尋找滿足檢測(cè)深度和檢測(cè)靈敏度條件下的最佳激勵(lì)頻率,是渦流檢測(cè)中一個(gè)重要影響因素。
檢測(cè)目標(biāo)是直徑φ0.4mm的氣孔缺陷,其中心與帶鋼上底面的距離t=2.1mm。如果能保證靈敏度的情況下檢測(cè)到該缺陷,那么渦流滲入的深度肯定可以達(dá)到銅板的底部。為了能檢測(cè)到深度為2.1mm的氣孔缺陷,選擇不同的頻率,初步擬定仿真頻率范圍為1~200kHz。圖4為針對(duì)存在上述缺陷情況下,采用不同頻率,仿真求得阻抗改變值ΔZ的幅值變化趨勢(shì)。以幅值的大小來衡量信號(hào)的強(qiáng)弱。
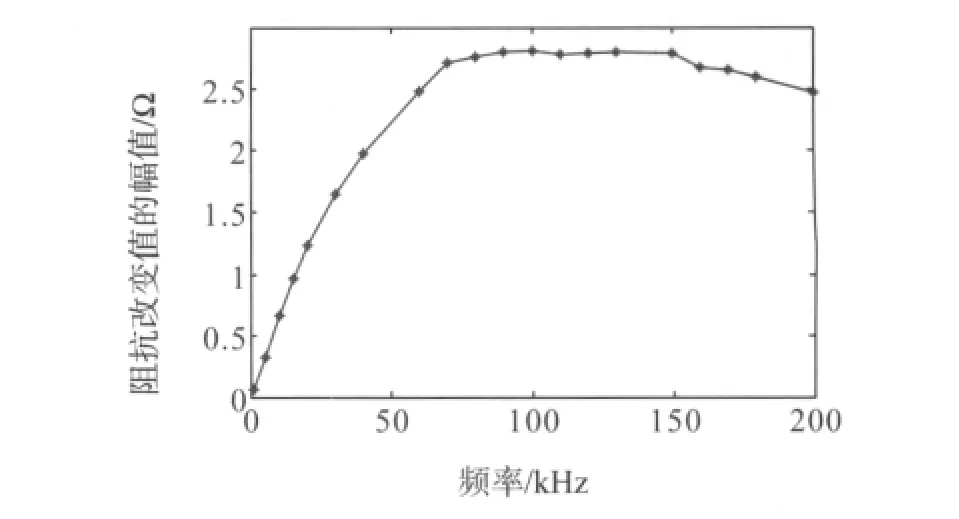
圖4 不同頻率下ΔZ幅值變化趨勢(shì)
從圖中可以看出,當(dāng)頻率<80kHz時(shí),信號(hào)幅值隨著頻率的增加而增大;當(dāng)達(dá)到80~150kHz時(shí),信號(hào)幅值達(dá)到一個(gè)最大范圍;當(dāng)超過150kHz后,信號(hào)幅值趨于減小。該圖形所展現(xiàn)的規(guī)律與渦電流的滲透深度和檢測(cè)靈敏度是一對(duì)矛盾相符合。可知當(dāng)頻率達(dá)到80kHz左右時(shí),檢測(cè)靈敏度已達(dá)到要求,根據(jù)頻率越低渦流滲透深度越大來考慮,檢測(cè)該薄板的最佳頻率為80kHz。
3.2 氣孔缺陷仿真信號(hào)分析
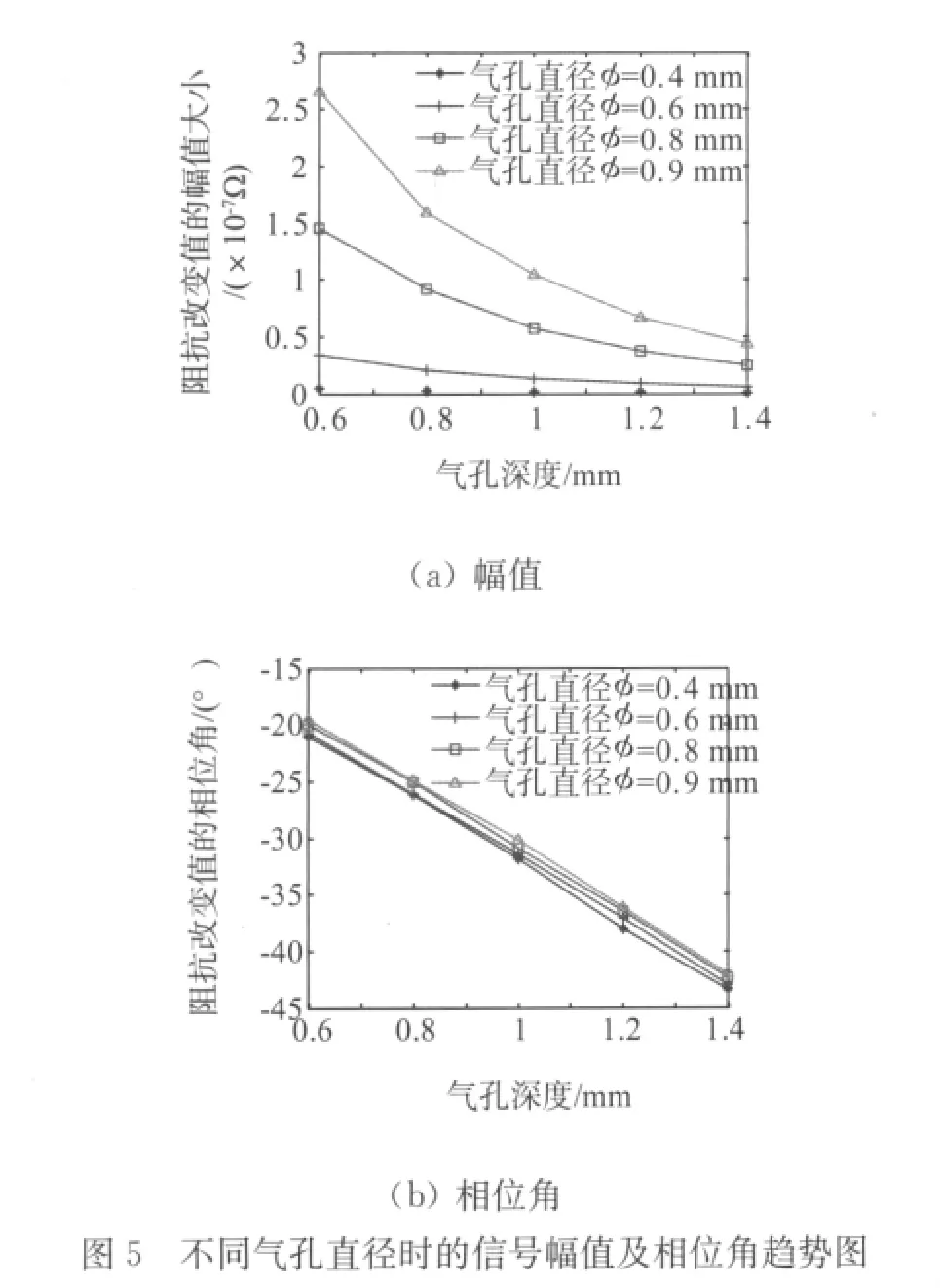
該部分采用的線圈激勵(lì)頻率為80kHz。建模計(jì)算時(shí),令氣孔直徑φ為0.4,0.6,0.8,0.9mm,氣孔中心與帶鋼上表面的距離t為0.6,0.8,1.0,1.2,1.4mm,在每一直徑下計(jì)算不同t的阻抗變化值。圖5(a)為氣孔直徑φ為0.4,0.6,0.8,0.9mm 時(shí)的不同深度位置的信號(hào)幅值趨勢(shì)圖,圖5(b)為信號(hào)相位角趨勢(shì)圖。因?yàn)槌R?guī)渦流檢測(cè)信號(hào)的處理只考慮信號(hào)的幅值和相位角,所以在此只研究這兩者的規(guī)律。
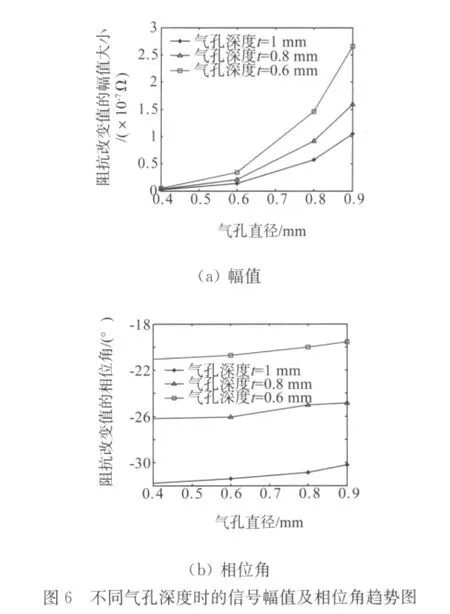
從圖5可以看出,當(dāng)氣孔直徑一定時(shí),隨著氣孔中心離上表面的距離越深,阻抗改變值的幅值信號(hào)越小,氣孔缺陷對(duì)渦流信號(hào)的干擾越弱;氣孔中心離上表面的距離一定時(shí),直徑越大,阻抗改變值的幅值信號(hào)越大。這種規(guī)律與渦流檢測(cè)原理相符合。從圖6的結(jié)果可以看出,當(dāng)氣孔中心離上表面的深度值增大時(shí),信號(hào)對(duì)應(yīng)的相位角近似呈正比例減小;而在相同的深度位置,不同直徑的氣孔對(duì)應(yīng)的相位角的大小近似相等。所以通過這個(gè)規(guī)律可以使用相位角的信息來確定氣孔的深度值。
氣孔直徑φ為0.4,0.6,0.8,0.9mm,氣孔中心與帶鋼上表面的距離t為0.6,0.8,1.0mm,在每一深度距離下計(jì)算不同直徑的阻抗變化值。圖6(a)為深度位置t為0.6,0.8,1.0mm時(shí)的不同氣孔直徑的信號(hào)幅值趨勢(shì)圖,圖6(b)為信號(hào)相位角趨勢(shì)圖。從圖6(a)的結(jié)果可以看出,在同一深度位置,氣孔直徑增大時(shí)對(duì)應(yīng)的信號(hào)幅值也增大。從圖6(b)可知,在同一深度位置,氣孔直徑增大時(shí)對(duì)應(yīng)的信號(hào)相位角也增大。但在同一深度位置,最大信號(hào)相位角與最小相位角的差值<3°。在此可以充分證明,通過相位角來判斷缺陷的深度是完全可行的。
4 結(jié)論
通過有限元軟件ANSYS模擬了渦流檢測(cè)薄板內(nèi)部氣孔型缺陷這一過程,求出了檢測(cè)該銅板的最佳激勵(lì)頻率。在該激勵(lì)頻率下,得出了氣孔直徑越大、深度越淺,幅值與相位角呈增大趨勢(shì),氣孔直徑越小、深度越深,幅值與相位角呈減小趨勢(shì)。所得結(jié)論與實(shí)際理論情況相符合,證實(shí)了仿真的可靠性。
[1]馮蒙麗,蔡玉平,趙建君,等.ANSYS在電磁無損檢測(cè)中的應(yīng)用[J].四川兵工學(xué)報(bào),2009,30(6):25-29.
[2]任吉林,林俊明.電磁無損檢測(cè)[M].北京:科學(xué)出版社,2008.
[3]王晶,潘紅良.渦流檢測(cè)薄板內(nèi)空氣型缺陷的ANSYS仿真研究[C].全國(guó)第九屆無損檢測(cè)學(xué)術(shù)年會(huì).中國(guó)機(jī)械工程學(xué)會(huì)無損檢測(cè)分會(huì),上海,2010:535-539.
[4]王春蘭,張鋼,董魯寧,等.電渦流傳感器的有限元仿真研究與分析[J].傳感器與微系統(tǒng),2006,25(2):41-46.
[5]Hiroyuki Fukutomi,Toshiyuki Takagi,Junji Tani,et al.Numerical Evaluation of ECT Impedance Signal due to Minute Cracks[C].IEEE TransMagn,1997,33(2):2123-2125.
[6]Pingjie Huang,Guangxin Zhang,Zhaotong Wu,et al.Inspection of defects in conductive multi-layered structures by an eddy current scanning technique:simulation and experiments[C].NDT&E International,2006(39):578-584.
[7]孫明禮,胡任喜,崔海蓉.Ansys10.0電磁學(xué)有限元分析實(shí)例指導(dǎo)教程[M].北京:機(jī)械工業(yè)出版社,2007.

