用于增大景深的四次復合型旋轉對稱相位模板

莫緒濤

（安徽工業大學 數理學院，安徽 馬鞍山 243002）

用于增大景深的四次復合型旋轉對稱相位模板

莫緒濤

（安徽工業大學 數理學院，安徽 馬鞍山 243002）

旋轉對稱型大景深相位模板的設計是波前編碼大景深成像技術中的關鍵技術之一.四次方型相位模板（QPM）是旋轉對稱型大景深相位模板家族中的典型代表.但QPM對應系統隨離焦程度的不同而具有不同的成像特性，即離焦不變性較差.為了在QPM的基礎之上得到具有良好的離焦不變性的相位模板，提出了利用兩個互為相反數的QPM的分區復合得到新相位模板的方法：首先，按照半徑等分法或面積等分法將相位模板分成偶數個環形區域，然后，相鄰分區相位采用兩種不同的QPM相位函數.系統的幅度傳遞函數曲線以及幅度傳遞函數密度圖均表明，使用了兩種相位模板的成像系統具有良好的離焦不變性.

波前編碼；增大景深；相位模板；優化

1 引言

增大光學成像系統的景深是應用光學領域的研究方向之一.當前用來增大景深的技術主要集中在波前編碼[1]技術.即在普通光學成像系統的孔徑光闌處放置一塊特殊設計的相位模板對成像光束調制，得到對離焦影響不敏感的圖像，然后再經過圖像復原處理得到大景深圖像.波前編碼大景深成像技術具有廣泛的應用前景，比如在顯微成像系統、安保監控成像系統、機器視覺的成像系統中可以顯著增大光學成像系統的景深范圍，在空間遙感成像系統中，可以減輕因溫度改變、大氣干擾等造成的離焦問題，避免設計復雜的溫度補償裝置，從而降低系統的結構復雜性以及成本.

波前編碼技術的兩個關鍵點：一是相位模板的設計；二是圖像復原算法的研究.本文針對相位模板進行研究.目前相位模板主要包括以三次方型CPM為代表的非旋轉對稱型相位模板[1-4]，還有以四次相位模板[5]為代表的旋轉對稱型相位模板[5-6].非旋轉對稱相位模板一般具有景深增大倍數高的優點，但加工和檢測較為困難，此外，一般必須進行圖像復原處理之后才能像普通光學成像系統得到的圖像一樣直接使用.旋轉對稱型相位模板對應系統的景深增大倍數較小，但是加工和檢測相對容易，并且圖像傳感器上獲得的圖像可以直接應用而無需圖像復原，所以適用于全光型實時大景深成像系統之中.

在對旋轉對稱型相位模板的主要代表QPM進行研究后發現，QPM對應系統的特性隨著離焦程度的改變也隨著改變.而另一方面，通常希望大景深成像系統在景深范圍之內都具有基本一致的成像特性.所以，在QPM的基礎之上如何達到上述目的是一個值得研究的內容.本文提出基于兩個參數互為相反數的QPM的分區復合方法來達到大景深的目的.

2 分區復合型QPM的設計

利用非相干光學成像系統的PSF表達式以及穩相法可以推導出四次型圓對稱相位模板對應的相位函數表達式[5]為：

其中，j代表虛數單位，k代表波數.為了簡化，我們把表達式中的ka記作α，kb記作β.QPM相位模板對應系統的成像特性具有如下兩個特點：一是在景深范圍之內不具有較好的一致性，二是當模板參數取相反數時，成像特性是之前特性零離焦的鏡像.這可以由對應系統的MTF密度圖直觀說明，如圖1所示，橫坐標代表離焦參數，縱坐標為歸一化空間頻率，灰度值代表MTF的響應值.

我們一般希望大景深成像系統在景深范圍之內具有較好的離焦不變性，同時系統的景深所對應的離焦參量關于零離焦左右對稱.如何利用QPM實現上述目標呢？考慮到互為相反數的QPM對應系統特性的對稱性，將它們恰當地組合在一起或許可以達到景深范圍之內具有離焦不變性的性質，同時滿足景深關于零離焦對稱.借鑒多環分區型相位模板[7]的設計方法，將相位模板按某種原則分成多個環帶區域，相鄰環帶對應的相位函數參數互為相反數.分區的方法可以有：半徑（長度）等分法和面積等分法.新得到的兩種相位模板的表達式為：

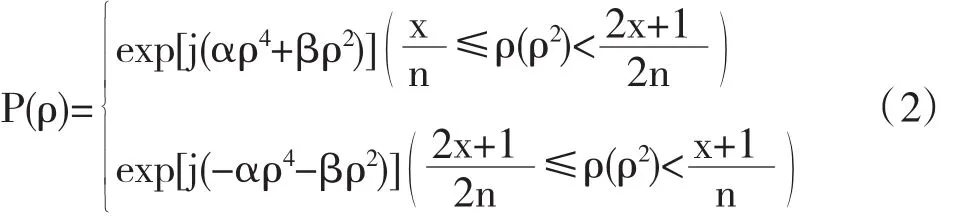
式中區間表達式ρ(ρ2)的ρ和ρ2分別代表半徑長度等分法和面積等分法.n代表分區參數，相位模板的環帶總數為2n，x取整數，x取值范圍為[0,n-1].可見，此時的相位模板由三個可變參數控制：分區數n、以及QPM的兩個參數α和β.

3 相位模板的優化及特性研究

為了更好地驗證模板具有較好的景深延拓特性，首先必須找到合適的模板參數，而模板參數一般而言對應某種系統設計目標.因此，接下來應該建立相位模板的優化模型，并根據成像系統的具體需求得到對應的優化參數.根據大景深優化設計的原則[8]，文中采用的優化模型表示為：

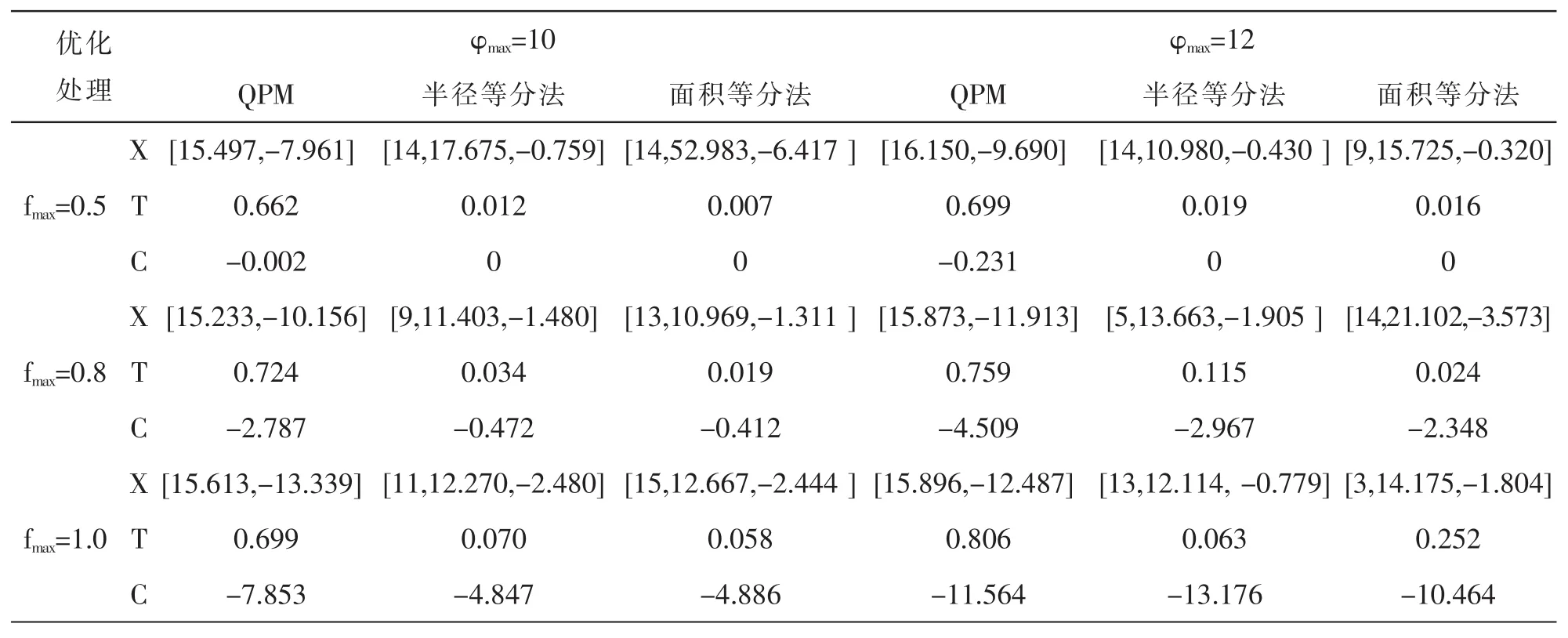
表1 不同景深、空間頻率需求時，相位模板對應的優化結果

其中，T(X;fmax,φmax)為優化模型的目標函數，X為相位模板的待優化參數向量，H(f,φ)為系統的光學傳遞函數（OTF），f為空間頻率（對應成像分辨率），φ 為離焦參數（φ=kW20），fmax和 φmax用來表示系統欲達到的分辨率和景深范圍.不同的成像系統對MTF的最小響應值Vmin有著不同的要求，對于機器視覺系統而言一般大于0.05即可，文中采用0.05.

利用上述優化模型，并就幾種常見的系統設計要求，對一般的QPM以及文中給出的改進的兩種分區型QPM進行了優化處理，優化結果如表1所示.對于每一種類型的相位模板，對應某種設計要求，優化結果包括三部分：優化參數（表格中的行X），優化目標函數值（表格中的行T），滿足限制條件的程度（表格中的行C）.其中，QPM對應的X為[α,β]，兩種分區型 QPM 對應的 X 為[n,α,β]；優化目標函數值T越小，表明離焦不變性越好；限制條件滿足程度參量C越大，表明系統滿足限制條件的程度越好，完全滿足條件時取值為0.

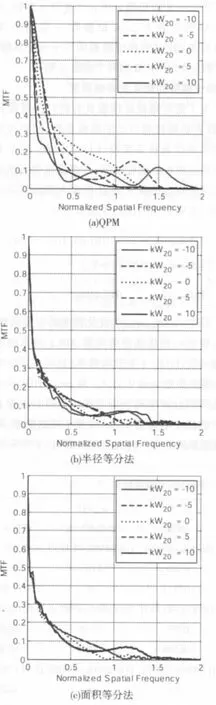
圖2 相同設計前提下的幾種相位模板的MTF曲線

圖3 相同設計前提下的幾種相位模板的MTF密度圖及二值化MTF密度圖

從表1可以看出，兩種分區型QPM對應的優化目標函數都小于普通QPM所對應目標函數值，表明了改造后的兩種QPM都較原來的QPM具有理想的離焦不變性，進一步比較會發現面積等分法的離焦不變特性要優于半徑等分法.限制條件滿足程度方面具有類似的結論.從而面積等分法可以作為更理想的相位模板得以應用.

為了進一步分析兩種分區型QPM對應系統的特性，不失一般性，接下來以fmax=0.8和φmax=10條件下對應的優化模板進行對比研究.對應的MTF曲線和MTF密度圖分別如圖2、圖3所示.從圖2可以明顯看到，兩種分區型QPM的離焦不變性的改善.面積等分法與半徑等分法相比，對于高斯物面相同程度的離焦具有更加一致的成像特性.這一點從圖3中可以更加明顯地看出，因為面積等分法的MTF密度圖關于零離焦具有很好的對稱性.圖3中的二值化MTF密度圖，是通過對MTF密度圖進行二值化處理得到的，二值化閾值即為優化時所要求達到的最小MTF響應值（文中為0.05），二值化閾值圖中的橫線代表此時系統要求的歸一化頻率響應（圖中為0.8）.從圖中可以看出，兩種改造后的相位模板對應系統的景深約為原來QPM對應系統景深的2倍.

4 結論

通過將互為相反數的兩個四次方型相位模板按照半徑等分法和面積等分法得到兩種不同的新的旋轉對稱型相位模板，數值分析結果表明，兩種相位模板都比原來的相位模板具有更好的離焦不變性、景深增大倍數，同時也能夠更好地滿足系統在景深范圍之內對MTF的響應要求.更進一步來說，面積等分法得到的相位模板對于零離焦前后相同程度離焦具有一致的成像特性.

〔1〕Dowski E R，Cathey W T.,Extended Depth ofField through Wave-FrontCoding[J],Applied Optics，1995，34(11)：1859～1866.

〔2〕Yang Qingguo，Liu Liren，Sun Jianfeng,Optimized phase pupilmasksforextended depth offield [J],OpticsCommunications,2007,272(1):56～66.

〔3〕Sherif S.Sherif,W.Thomas Cathey,Ed R.Dowski，Phase plate to extend the depth of field of incoherent hybrid imaging systems[J]，Applied Optics，2004,43(13)：2709～2721.

〔4〕HuiZhao,YingcaiLi,Optimized sinusoidal phase mask to extend the depth of field of an incoherent imaging system [J], OPTICS LETTERS,2010,35(2):267-269.

〔5〕S.Mezouari ,A. R. Harvey, Phase pupil functions for reduction of defocus and spherical aberrations[J],OPTICS LETTERS,2003,28:771–773.

〔6〕FengZhou,RanYe,GuangweiLi,Haitao Zhang,Dongsheng Wang,Optimized circularly symmetric phase mask to extend the depth of focus[J],J.Opt.Soc.Am.A,2009,26(8):1889-1895.

〔7〕莫緒濤，劉文耀，王晉疆.大景深光學成像系統關鍵技術的研究[J].光電工程，2007，34(12):129-133.

〔8〕莫緒濤，劉文耀，王晉疆.大景深相位模板的個性化設計[J].光電工程，2008，35(5)：85-88.

TP391.41

A

1673-260X（2012）06-0012-04

本文是安徽工業大學青年教師科研基金項目（QZ201116）