非規則幾何結構平面陣列的DOA估計性能

張利強,全厚德,崔佩璋

(軍械工程學院信息工程系,石家莊050003)

1 引 言

隨著現代戰場環境的日益復雜化,空間目標日益增多,對目標源進行精確定位就需要提供精確的二維信息。確定目標的DOA(來波方向),在對敵方軍事目標實施全面的偵察、測向定位和監視中就顯得尤為重要,是獲取戰場制電磁權與實施精確打擊的首要前提。

近年來,以基于接收信號的協方差矩陣特征分解理論的子空間類方法MUSIC算法為代表的空間譜估計技術在雷達、通信、電子對抗等領域得到了廣泛的應用[1]。在空間譜估計中,采用經典陣列結構形式的陣列得到了深入的研究。但是對于采用固定陣列結構的陣列形式而言,其對布設陣列所需的空間有嚴格的要求。現實應用中,由于受實際環境的限制,天線陣列的陣元數量及其陣列結構都會受到一定的影響,陣列結構不一定滿足線陣等經典陣列形式,陣列結構往往是非規則的任意陣型,這就會給精確測向帶來困難,因此,研究非規則型天線陣列的超分辨測向具有重要的實際意義。

對非規則陣列的測向,學者們進行了一定程度的研究。文獻[2-4]研究了非規則陣列的優化和合成,文獻[5]僅對空間任意四元陣測向進行了研究,文獻[6]對陣列結構與測向性能的關系進行了分析。但是,這些研究成果對非規則陣列的測向模糊性討論較少。本文推導了適用于非規則結構平面陣列的MUSIC算法,完成了對空間多目標信號的DOA估計,同時分析了非規則平面陣列的陣列結構對測向模糊性的影響,以期為人們選擇合適的陣列結構提供依據。

2 非規則陣列測向數學模型

在圖1中的空間三維坐標系OXYZ,假設M 個陣元在平面XOY內組成任意幾何結構形狀的平面陣列,以某一陣元作為參考陣元(即位于坐標原點O),點Ai為平面XOY內中第i個陣元的位置,其坐標為(xi,yi)。假設空間有 N個不相關的遠場信號sj(t)(1≤j≤N),分別以不同的方向入射到該平面陣列,遠場信號為均值為零的平穩過程,各陣元接收的噪聲為獨立的加性高斯白噪聲,第j個信號來波方向的方位角和俯仰角為(θj,φj)。

圖1 非規則陣列模型Fig.1 Irregular geometry plane array′s model

在圖1中,連接O和A點,從A點作垂直于入射信號的垂線,垂點為B點,其坐標為(x,y,z),由電磁波傳播理論可知OB就是陣元A與參考陣元之間在Δt內傳播的距離,由幾何關系得

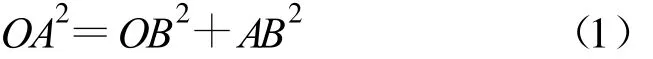
其中,AB2=(xi-x)2+(yi-y)2+z2,B點坐標分別為 x=OBsinφ cosθ,y=OBsinφ sinθ,z=OBcosφ。將B點坐標代入式(1),對其進行化簡,可得陣元A與參考陣元間的波程差τ:

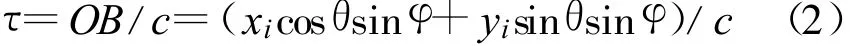
測向陣列的輸出矩陣形式為

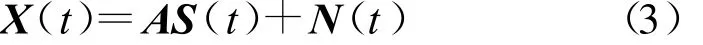
其中,A為陣列流形矩陣,S(t)為空間信號矢量,N(t)為噪聲矢量,即:

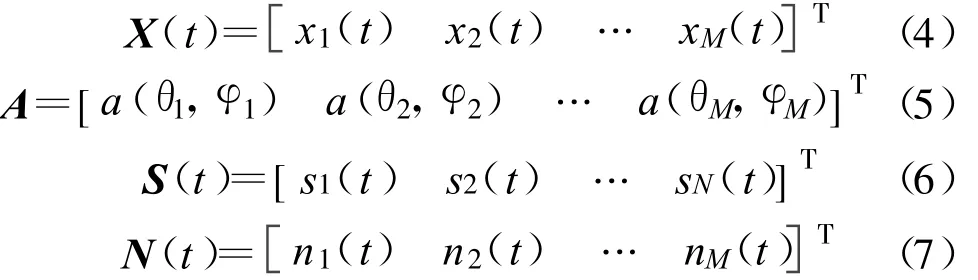
式(5)中,導向矢量

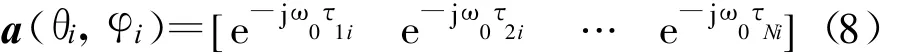
式中,ω0=2πc/λ,τNi表示第i個信號到達第N 個陣元時對參考陣元的時延。

3 基于MUSIC算法的高分辨二維測向

基于協方差矩陣特征分解理論的子空間類方法MUSIC算法一直受到人們的重視,其能夠提供信號參量的漸進無偏估計,使估計的均方差接近CR界,在特定條件下具有很高的分辨力、估計精度和穩定性。該算法的提出促進了特征結構類算法的興起和發展,已成為空間譜估計理論體系中的標志性算法。

文獻[7]利用3個直線陣進行組合實現了分別估計一維DOA,但其對非規則結構平面陣并不適用。對于非規則結構平面陣,基于MUSIC算法實現二維DOA估計的主要步驟如下。

(1)參數初始化。設置各陣元位置坐標以及信號源的入射角度,并建立導向矢量矩陣A。

(2)通過建模隨機產生窄帶信號源及噪聲數據,建立陣列接收數據的矩陣形式X(t)[8]。

(4)對R進行特征值分解,按照降序排列其特征值及對應的特征向量。

(5)從第三步知R的獲得是通過有限的采樣數據實現的,因此其最小特征值并不相等,依據信息論最小描述長度準則對信源數目q進行估計。

(6)從第五步得到最小特征值的個數為(M-q),進一步求出特征矢量 VD+1,VD+2,…,VM,最小特征值對應的特征矢量構成的噪聲子空間 UN=[VD+1,VD+2,…,VM];

(7)計算MUSIC譜函數PMUSIC:

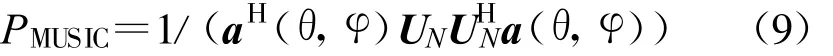
使 θ、φ分別在 0～ 360°、0～ 90°變化,對式(9)進行計算,繪制二維曲線并在二維空間進行譜峰搜索,即可估計得到信號源的方位角和俯仰角。高分辨二維DOA估計的流程圖如圖2所示。

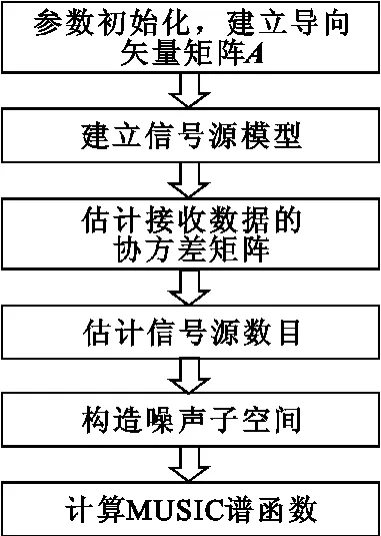
圖2 二維DOA估計的算法流程Fig.2 Flow of two-dimensional DOA estimation

在圖2中,關鍵工作是建立導向矢量矩陣A,其具體過程在非規則陣列測向數學模型中有詳細的研究。

4 測向模糊性分析

在圖1所示的M元非規則結構平面陣中,天線陣的陣列流形如式(8)所示。對于復指數函數e-jt,其對于t是以2π為周期的周期函數,因此對于一個確定的 a(θ),可能存在互異的角度 θ1、θ2使得a(θ1)=a(θ2)成立,即并不能保證信號方向估計的唯一性。

假設信號入射角度為θ,若存在測向模糊,則必存在另一個入射角度 ψ,使得 a(θ)=a(ψ)成立,即向量的各個分量相等,由此可得

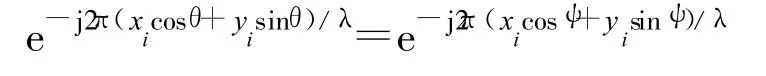
根據復指數函數的周期性,可得

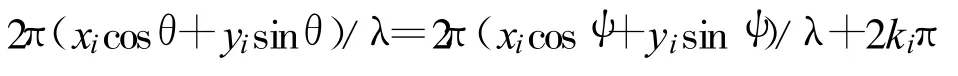
其中,ki(i=1,2,…,M)為整數或零。對上式進行整理:

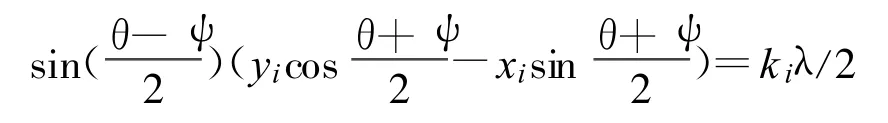
在圖1中,設任意陣元 A與x軸夾角為θA,則陣元A的坐標滿足

對上式進一步整理可得

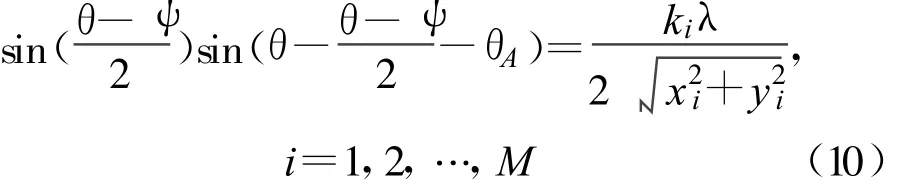
對于M元非規則結構平面陣,在采用MUSIC算法測向時,在信號波達方向 θ上,對任意的-π≤(θ-ψ)/2≤π,和式(10)(其中 ki為整數或 0),如果有且僅有 θ=ψ時式(10)成立,則此時不存在測向模糊。若θ-ψ≠0時式(10)仍成立,那么此時就存在測向模糊。所以,是否存在測向模糊可歸根于式(10)中ki是否有整數解或零解。測向模糊存在與否,取決于陣列的各陣元位置及信號的波長。在設計無模糊測向的陣列時應綜合考慮這兩方面因素。

5 仿真和分析

實驗1 取陣元數為6元的平面陣,陣列結構分別采用矩形平面陣和任意形狀平面陣,矩形面陣的各陣元坐標為(0,0)、(2,0)、(4,0)、(0,2)、(2,2)、(4,2),任意形狀平面陣的各陣元坐標為(0,0)、(1,0)、(3,1)、(1,3)、(5,3)、(2,5)。空間信源個數為 2,入射角度分別為(20°,30°)和(110°,50°),信噪比假設為-10～20 dB,快拍數取512,信號頻率為150 MHz。做100次蒙特卡洛實驗分析矩形平面陣和任意形狀平面陣的測向精度。

為了描述兩種平面陣列的測向精度,定義二維測向時角度的均方根誤差(RMSE)為

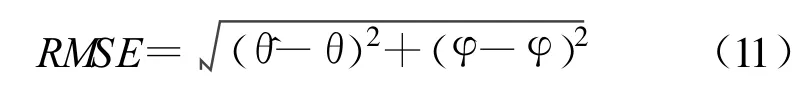
式中,θ、φ表示信號方位角和俯仰角的真值 , θ、 φ表示信號方位角和俯仰角的實驗測量值。

在仿真過程中,改變信噪比,以5 dB為步長從-10 dB變化到20 dB,以100次測量結果的平均值作為測量結果。測向角度的RMSE與信噪比的關系曲線如圖3和圖4所示。

圖3 信號(20°,30°)的 R MSE隨SNR變化曲線Fig.3 Signal(20°,30°)variation curve of R MSE and SNR

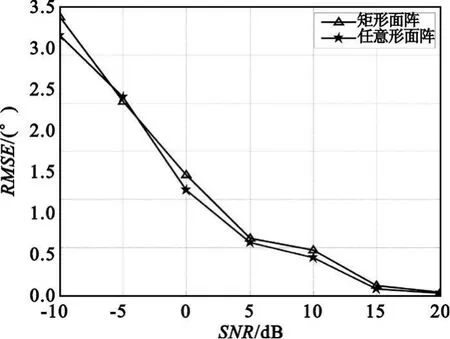
圖4 信號(110°,50°)的 R MSE隨SNR變化曲線Fig.4 Signal(110°,50°)variation curve of R MSE and SNR

從圖3和圖4可以看出,對不同的信號入射角度,在信噪比變化過程中,在整體趨勢上6元矩形平面陣列的均方根誤差(RMSE)要大于陣元位置坐標任意的任意形結構平面陣列。兩種陣形相比,任意形平面陣列的測向精度更好些。

實驗2 取實驗1中的兩種6元平面陣列,空間信源個數為 2,入射角度分別為(10°,20°)和(80°,60°),在信噪比為5 dB時,做100次蒙特卡洛實驗分析矩形平面陣和任意形狀平面陣的二維MUSIC譜曲線圖。

矩形平面陣的MUSIC譜曲線圖及其等高線圖如圖5和圖6所示。

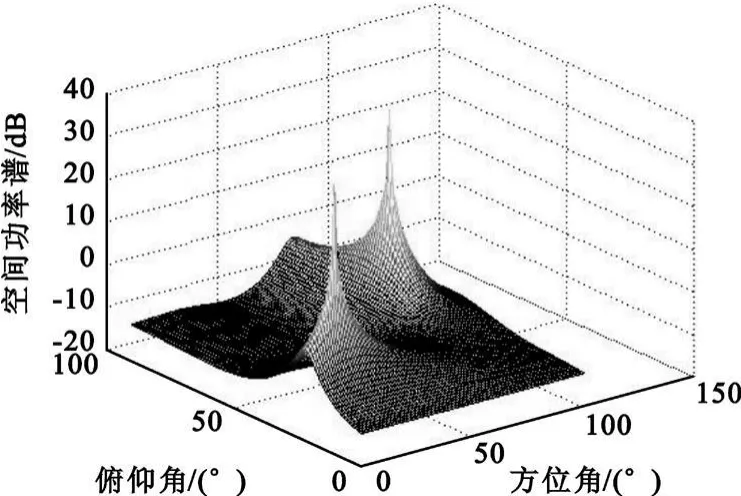
圖5 矩形平面陣的譜曲線圖Fig.5 Spectrum of rectangle plane array

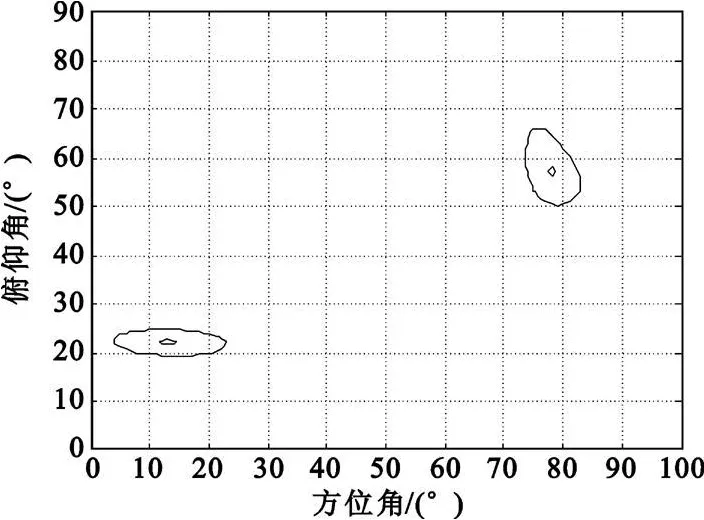
圖6 矩形平面陣譜曲線的等高線圖Fig.6 Spectrum′s contour of rectangle plane array

任意形平面陣列的MUSIC譜曲線圖及其等高線圖如圖7和圖8所示。

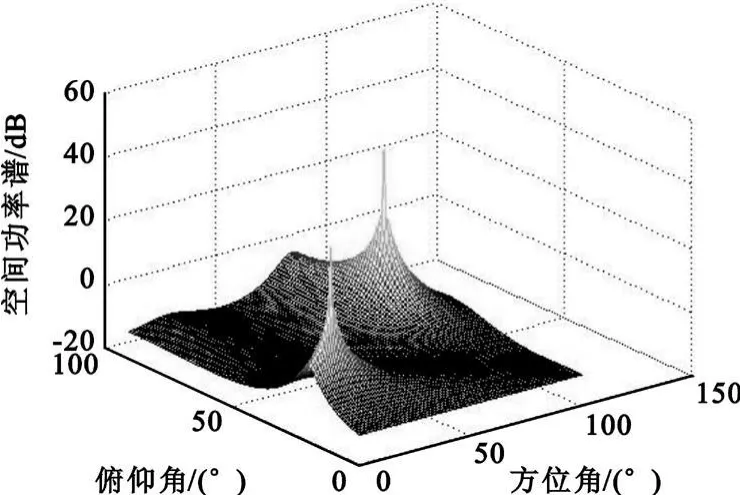
圖7 任意形平面陣的譜曲線圖Fig.7 Spectrum of arbitrary plane array

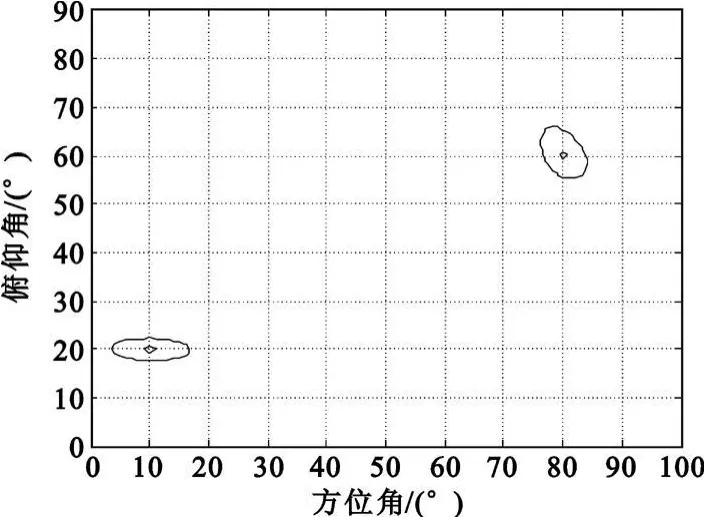
圖8 任意形平面陣譜曲線的等高線圖Fig.8 Spectrum′s contour of arbitrary plane array

從圖5～8可看出,在相同條件下,矩形平面陣和陣元位置坐標任意的平面陣列兩者都能夠比較準確地實現信號的DOA估計,而且后者得到的空間功率譜的譜峰更尖銳,指向更精確。

實驗3 對實驗1中的兩種6元平面陣列,理論分析其測向模糊性。將矩形平面陣和任意形平面陣的各陣元位置坐標代入式(10),經過Matlab計算發現在矩形平面陣時ki不存在,故該矩形平面陣在本實驗條件下存在測向模糊問題,這一點從圖6也可得到驗證。在對任意形平面陣經過計算后,發現滿足條件的ki存在,因此該陣列不存在測向模糊問題。通過進一步分析可知,測向模糊與陣元位置及信號波長有直接的關系,在圖1所示的坐標系下設計任意形平面陣時,應首先保證位于x軸上的第一個陣元到參考陣元的距離d>λ/2,否則必存在模糊問題。

以上實驗驗證了數學模型對非規則結構平面陣列二維測向的有效性,為后續工程實踐中應用論文的研究成果提供了可行性,具有一定的實用性。

6 結束語

天線陣的陣列結構對其測向性能有著直接影響。針對實際環境對陣列結構的約束和實際應用中的二維測向問題,本文建立了非規則平面陣列的通用測向數學模型,利用經典MUSIC算法對二維測向進行了研究,分析了陣列結構對測向模糊的影響。理論分析和仿真結果表明,論文提出的數學模型對非規則結構平面陣列的測向具有實用性,可廣泛應用于任意平面空間的二維測向研究。在非規則陣列結構中如何選取最簡單的陣型以符合測向的具體要求,將是后續研究工作的重點。

[1]王永良,陳輝,彭應寧,等.空間譜估計理論與算法[M].北京:清華大學出版社,2009.WANG Yong-liang,CHEN Hui,PENG Ying-ning,et al.SpatialSpectrum Estimation Theory and Algorithm[M].Beijing:Tsinghua University Press,2009.(in Chinese)

[2]陳客松,何子述.平面稀布天線陣列的優化算法[J].電波科學學報,2009,24(2):193-198.CHEN Ke-song,HE Zi-shu.Synthesis Approach for Sparse Plane Arrays[J].Chinese Journalof Radio Science,2009,24(2):193-198.(in Chinese)

[3]Kumar B P,Branner G R.Generalized analytical technique for the synthesis of unequally spaced arrays with linear,planar,cylin-drical or spherical geometry[J].IEEE Transactions on Antennas and Propagation,2005,53(2):621-634.

[4]Trucco A,Omodei E,Repetto P.Synthesis of sparse plannar arrays[J].Electronics Letters,1997,33(4):1834-1835.

[5]何軻,相敬林,韓鵬,等.空間任意陣的MUSIC算法性能研究[J].計算機測量與控制,2010,18(3):688-690.HE Ke,XIANG Jing-lin,HAN Peng,et al.Performance Analysis of MUSIC for Arbitary Array[J].Computer Measurement&Control,2010,18(3):688-690.(in Chinese)

[6]劉洪盛.高分辨測向陣列幾何結構研究[D].成都:電子科技大學,2009.LIU Hong-sheng.Geometry of Array with High Resolution in Direction Finding[D].Chengdu:University of Electronic Science and Technology of China,2009.(in Chinese)

[7]戰金龍,胡國平.一種新的二維MUSIC算法的研究[J].通信學報,2004,25(4):69-74.ZHAN Jin-long,HU Guo-ping.A Novel 2-D MUSIC Algorithm[J].Journal of China Institute of Communications,2004,25(4):69-74.(in Chinese)

[8]許凌云,張小飛,許宗澤.平面陣列下的二維角度和頻率聯合估計[J].應用科學學報,2011,29(2):187-194.XU Ling-yun,ZHANG Xiao-fei,XU Zong-ze.Joint 2D Angle and Freq-uency Estimation Based on Uniform Square Array[J].Journal of Applied Science-Electronic and Information Engineering,2011,29(2):187-194.(in Chinese)