電四極透鏡中強流脈沖束的傳輸模擬

李超龍 石海泉 呂建欽

1 (華東交通大學基礎科學學院 南昌 330013)

2 (北京大學核物理與核技術國家重點實驗室 北京 100871)

在加速器的束流傳輸中，電四極透鏡是強聚焦元件，適用于各種低能粒子的聚焦，一般用于1MeV以下的束流聚焦。強流脈沖束在電四極透鏡中傳輸的模擬計算是一個相當復雜的問題，因為不同類型的粒子束分布產生不同的空間電荷場，而在束流運動過程中，空間電荷場也在不斷地變化，而且粒子運動的軌跡與空間電荷勢又是相互依賴的，最后，應當達到一種“自洽”的結果，在計算強流束的傳輸時求得自洽解是非常必要的[1]。

非強流脈沖束在電四極透鏡中傳輸時，束流中離子間的空間電荷力與外加聚焦力相比可以忽略，可以用TRANSPORT-EM程序進行計算。強流脈沖束在電四極透鏡中傳輸時，束流中離子間的空間電荷力與外加聚焦力相比不可忽略，但TRANSPORT-EM 程序不計入空間電荷力，因此不能計算強流束的傳輸[2-4]。此時可以用TRACE 3-D、PARMILA、PARMTEQ等程序進行計算，但是它們在計算強流束的傳輸時都不經過迭代計算，所得結果不是自洽解[5-11]。

為了得到強流脈沖束在電四極透鏡中傳輸時的自洽解，采用矩陣法給出電四極透鏡中束流的傳輸矩陣，采用優化方法實現給定的光學條件，采用迭代方法計求得自洽解。

1 電四極透鏡的傳輸理論

束流傳輸系統的設計與研究有矩陣法和軌跡方程法兩種數值計算方法。

矩陣法：根據束流傳輸理論，束流可用一個六維相空間橢球來描述，傳輸元件對束流運動的作用可以用傳輸矩陣算子表示。矩陣法就是根據給定的初始束流相空間橢球，通過計算傳輸矩陣算子，設計束流傳輸系統使得傳輸后的束流相空間橢球符合要求。

軌跡方程法：采用對帶電粒子在電磁場中的運動方程直接積分的方法來設計束流傳輸系統。積分中，各個傳輸元件所產生的電磁場是預先給定的，它既可以是實驗測量值，也可以是數值計算結果。

本文采用矩陣法描述脈沖束流在電四極透鏡中的傳輸。非強流脈沖束在電四極透鏡中的傳輸時，不需要計入空間電荷力，電四極透鏡的傳輸矩陣為：

國家自然科學基金項目（21063007），江西省科技支撐計劃項目（2010BGB00602），江西省教育廳科學技術研究項目（GJJ11677）資助

強流脈沖束在電四極透鏡中的傳輸時，需要計入空間電荷力，由于空間電荷場與束流粒子軌跡相互依賴，計算強流脈沖束傳輸的自洽解，必須把電四極透鏡的場作用區均勻分成若干個區間，每個區間 [ zi-1,zi]的傳輸矩陣為：

2 程序的計算方法

在計算束流在電四極透鏡中的傳輸時，先計算非強流脈沖束流的傳輸，采用優化方法自動調整元件的參數，束流粒子的軌跡通過傳輸矩陣的直接相乘計算得出；然后計算強流脈沖束的傳輸，采用迭代方法計算束流的空間電荷效應。計算束流的空間電荷效應時，首先，把電四極透鏡均分成i個區間，把束流流強分成j等份；其次，在第1區間，調用相應數組中的考慮空間電荷時電四極透鏡中的傳輸矩陣(式(2))，進行迭代計算，可以計算出第1區間的j級傳輸矩陣和j級束流包絡；再次，重復上述步驟，依次計算第 2至 i區間的j級傳輸矩陣和j級束包絡；最后，把元件第1至第i區間的j級傳輸矩陣依次連乘可以得到考慮空間電荷效應時電四極透鏡的總矩陣，替換原先存儲在相應數組中的不考慮空間電荷效應時電四極透鏡的總矩陣。下面介紹優化方法和迭代方法。

2.1 優化方法

最優化計算是加速器粒子動力學設計的重要手段，它不但能夠使設計方案更加合理，而且可以大大節省計算時間。本程序使用直接尋優優化方法，直接尋優方法不需要計算目標函數的導數，它們適合于這樣一些問題：目標函數非常復雜，或者根本寫不出其解析式，故很難計算其導數。直接尋優方法屬于共軛梯度法，共軛梯度法是介于最速下降法與牛頓法之間的一個方法，它僅需利用一階導數信息，但克服了最速下降法收斂慢的缺點，又避免了牛頓法需要存儲和計算Hesse矩陣并求逆的缺點，它的每一個搜索方向是互相共軛的，而這些搜索方向d僅僅是負梯度方向與上一次迭代的搜索方向的組合，不需要矩陣存儲。其優點是所需存儲量小，具有較快的收斂速度和二次終止性等優點，而且不需要任何外來參數。直接尋優方法的計算步驟為：

2.2 迭代方法

由雅可比迭代公式可知，在迭代的每一步計算過程中是用 x(k)的全部分量來計算 x(k+1)的所有分量，顯然在計算第i個分量時，已經計算出的最新分量, L ,沒有被利用。有理由認為新計算出來的分量可能比上次迭代得到的分量有所改善。希望充分利用新計算出來的分量以提高迭代解法的效率，這就是高斯-賽德爾迭代法。

本程序采用高斯-塞德爾迭代法，相比雅可比迭代法，高斯-賽德爾迭代法的優點是在電算時只需一組存儲單元，并且具有更快的收斂速度。本程序迭代方法的基本步驟為：

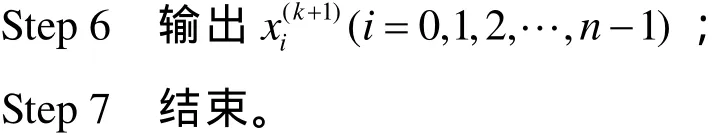
3 模擬計算

為了驗證理論和計算方法的科學性，保證本程序的可靠性，用本程序與TRANSPORT及TRACE 3-D進行了模擬計算比較。圖1為用來模擬計算的束流傳輸系統，由離子源、漂浮空間、電四極透鏡和靶室等組成。已知離子的初始能量為35keV，質量數和電荷數均為1。

圖1 束流傳輸系統Fig.1 Beam transfer system.

表 1為本程序與TRANSPORT在不同束流流強條件下的束流包絡曲線模擬值。當束流流強為5mA時，本程序和TRANSPORT的模擬值很接近，可以說明束流流強較小時，本程序和TRANSPORT的模擬值吻合較好，從而證明本程序模擬的可靠性。從表 1容易發現：隨著束流流強增大，本程序的模擬值也逐漸增大。這是因為束流流強越大，束流的空間電荷效應越強，空間電荷效應對束流包絡曲線橫向發散作用越顯著。

圖2為本程序和TRACE 3-D模擬不同束流流強條件下束流包絡曲線圖。從圖2(a)~(b)可以看出，本程序和TRACE 3-D的模擬圖吻合較好，說明在束流流強較小時，計算空間電荷效應時是否采用迭代方法對結果影響不大。從圖2(c)~(f)容易看出，隨著束流流強增大，本程序和TRACE 3-D的束流包絡曲線模擬圖的偏離逐漸增大。這是因為束流流強越大，空間電荷效應對束流包絡曲線橫向發散作用越顯著，非自洽解與自洽解的偏差越大。

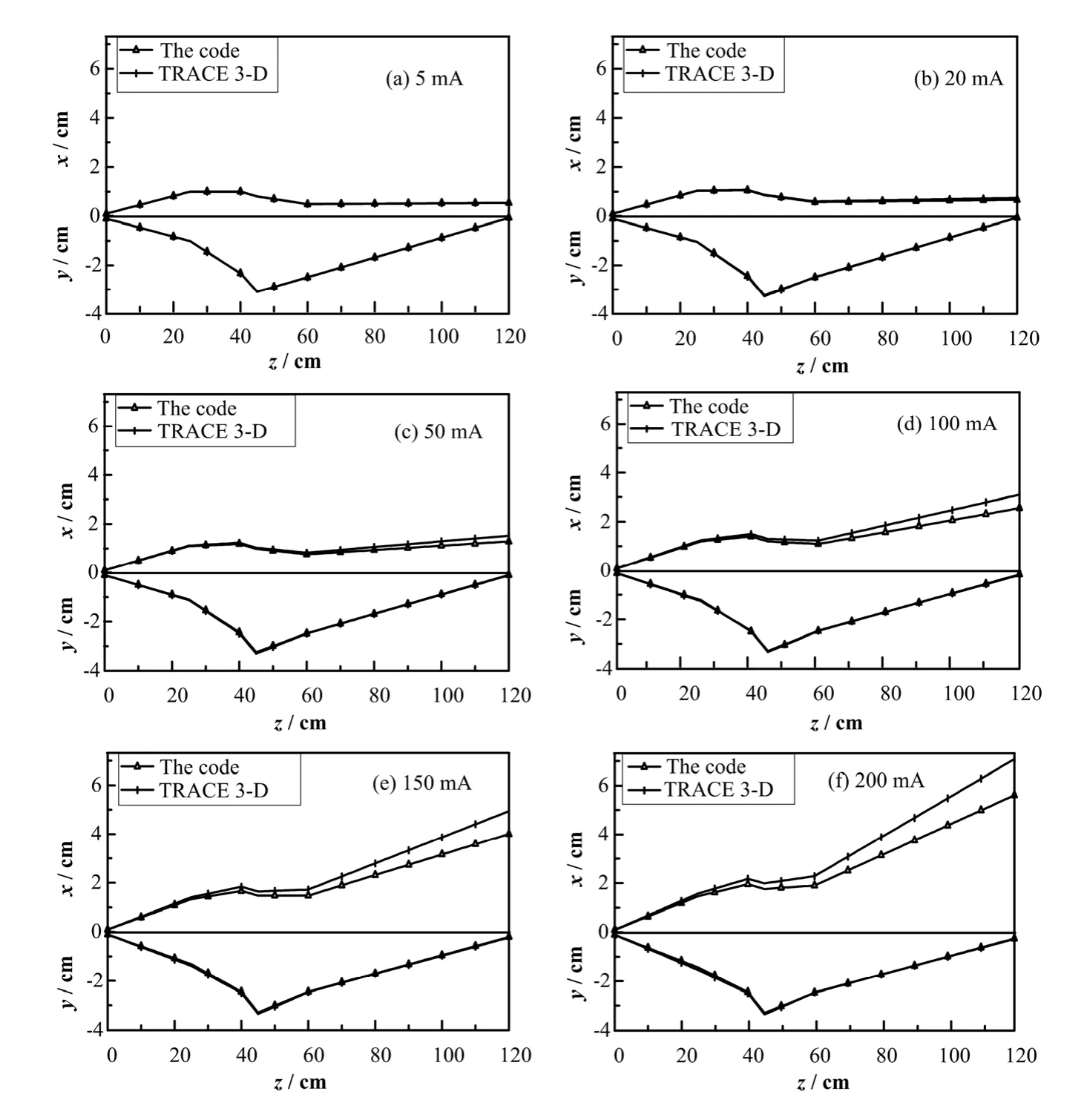
圖2 束流傳輸橫向包絡Fig.2 Transversal envelope of beam transfer.

4 結論

本文用矩陣法分析了強流脈沖束流在電四極透鏡中的傳輸矩陣，在此基礎上用迭代方法計算強流脈沖束流的傳輸。通過與其他現有模擬程序進行對比分析，可以看出，本程序的模擬結果是準確和可靠的。本程序在計算空間電荷效應時用迭代法逐次逼近，直到前后兩次計算結果之差滿足所要求的精度為止(即達到前后自洽)，因此其計算結果是自洽的，相比其他程序，具有優越性。模擬結果表明：束流流強越大，束流的空間電荷效應越強，空間電荷效應對束流包絡曲線橫向發散作用越顯著，非自洽解與自洽解的偏差也越大。

1 謝文楷. 帶電粒子束的理論與設計[M]. 北京: 科學出版社, 2009 XIE Wenkai. The theory and design of charged-particle beam[M]. Beijing: Science Press, 2009

2 茅乃豐, 肖美琴, 李增海. 用于束流輸運計算的TRANSPORT-EM程序[J].原子能科學技術, 1986, 20(6):117–119 MAO Naifeng, XIAO Meiqin, LI Zenghai. TRANSPORTEM—a program used for calculating beam line[J]. Atomic Energy Science and Technology, 1986, 20(6): 117–119

3 Gillespie G H, Hill B W. Particle optics and accelerator modeling software for industrial and laboratory beamline design[J]. Nuclear Instruments and Methods in Physics Research. Section B, 1998, 139(4):476–480

4 Becker R, Jameson R A. Simulation of RF-focusing in the RFQ matching section by IGUN[J]. Nuclear Instruments and Methods in Physics Research. Section A, 2006,558(1): 205–209

5 Takeda H, Stovall J E. Modified Parmila code for new accelerating structures[C]//Proceedings of the 1995 Particle Accelerator Conference.1995:2364–2366

6 Takeda H, Billen J H. Recent improvements in the Parmila code[C]//Proceedings of the 2003 Particle Accelerator Conference. 2003:3518–3520

7 Young L, Billen J. The particle tracking code Parmela[C]//Proceedings of the 2003 Particle Accelerator Conference. 2003: 3521–3523

8 Yang H R, Kim S H, Moon S I, et al. Commissioning scenario for L-band electron accelerator by Parmela code[C]//Proceedings of the 2007 Particle Accelerator Conference. 2007:2820–2822

9 Rusthoi D P, Lysenko W P. Further improvements in TRACE 3-D[C]//Proceedings of the 1997 Particle Accelerator Conference. 1997:2574–2576

10 Gillespie G H, Van Staagen P K. Knowledge rule base for the beam optics program TRACE 3-D[C]// Proceedings of the 1993 Particle Accelerator Conference. 1993:86–88

11 Lysenko W P. TRACE 3-D code improvements[C]//Proceedings of the 1997 Computational accelerator physics. 1997: 247–252