采用槽形梁橋面的大跨度鋼桁拱橋車橋動力分析*

唐俊峰，伊雪倩，郭向榮

(1.中南大學 土木工程學院，湖南 長沙 410075;2.云南交通職業技術學院公路學院，云南 昆明 650000)

大跨度鋼桁拱橋以其外形雄偉壯觀、跨越能力大、承載能力強等優點，成為橋梁建設中的有力競選方案。隨著我國經濟實力的增強和建設水平的提高，已經建成或在建的鋼桁拱橋的跨度不斷增大。值得注意的是，隨著鋼桁拱橋跨徑的不斷增大，列車通過橋梁時引起的橋梁響應也相應變大，對大跨度鋼桁拱橋進行車橋耦合振動分析研究顯得十分必要［1］。

鐵路大跨度鋼桁拱橋結構設計中，橋面的設計是一項重要內容。鐵路鋼橋橋面形式主要有明橋面和道碴橋面2種。明橋面由于其結構形式簡單，曾廣泛應用于鐵路橋梁，但是穩定性和耐久性較差，列車過橋時振動和噪聲較大，目前各國采用較少，而道碴橋面則應用較多。道碴橋面具有多種結構形式，其中預應力槽形梁形式的道碴橋面，具有建筑高度低、降噪效果好，斷面空間利用率高等優點，使其在新建鐵路大跨度鋼桁拱橋道碴橋面具有競爭力。槽形梁是一種下承結構，目前應用較多的是將槽形梁作為中小跨度橋梁上部結構的一種形式［2－6］，而直接把槽形梁用作鋼桁梁橋橋面形式的較少，對其開展的研究目前在國內外不多，因此對槽形梁的靜、動力學性能展開系統研究十分必要。

本文以某主跨為198 m的大跨度連續鋼桁柔性拱橋為研究對象，將列車、橋梁視為一個聯合的整體體系，建立了比較完善的車輛與橋梁的空間耦合振動分析模型，其中每節車輛動力模型考慮21個自由度，用空間梁單元模擬鋼桁拱橋主要構件，用梁格法模擬槽形梁橋面。采用計算機模擬的辦法，計算了ICE高速列車作用下的車橋空間耦合振動響應，分析了列車高速過橋時的行車安全性與乘坐舒適性，對該拱橋方案的剛度進行了評價，并從動力學角度探討大跨度鋼桁拱橋橋面采用槽形梁的可行性。

1 工程概況

本文的研究工程背景為一主跨198 m的連續鋼桁柔性拱橋，其總體布置如圖1所示。橋跨布置為(99+198+99)m，邊、中跨長度之比為 0.5，平、立面均位于直線上，雙線的間距為4.6 m。桁高15 m，柔性拱矢高為35 m，桁寬15 m。邊墩為變截面圓端形空心墩，主墩為變截面圓端形實體墩。群樁基礎，樁徑2 m，樁長55 m，行列式布置。橋面采用槽形道碴梁，槽形梁支承在鋼橫梁上，其縱向為一跨一聯的簡支梁，橫向為兩側帶翼板的“ш”形截面。

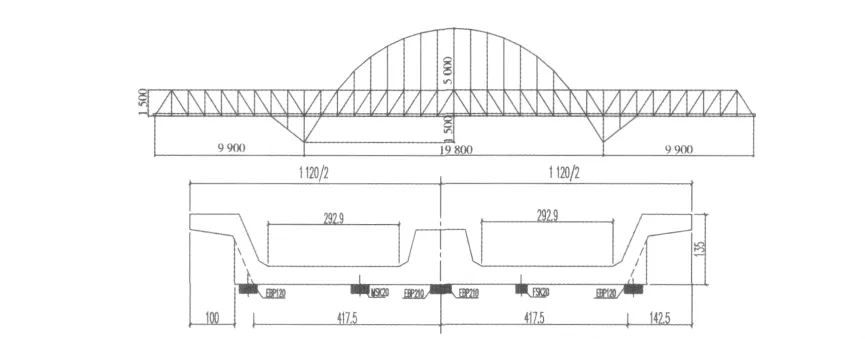
圖1 橋梁結構示意圖(單位:cm)Fig.1 Schematic diagram of bridge structure

2 列車－橋梁時變系統空間振動分析模型

2.1 列車(機車車輛)模型

對于二系懸掛的車輛(機車)，單節車輛由1個車體、2個轉向架及4個輪對構成，車體與前、后轉向架之間、轉向架與各輪對之間由線性彈簧和粘滯阻尼器相聯。在建立車輛分析模型時，采用文獻［1，7，8］中的基本假定:(1)車體、轉向架和輪對均假設為剛體;(2)不考慮機車、車輛縱向振動及其對橋梁振動與行車速度的影響;(3)輪對、轉向架和車體均作微振動;(4)所有彈簧均為線性，所有阻尼按粘性阻尼計算，蠕滑力按線性計算;(5)沿鉛垂方向，輪對與鋼軌密貼，即輪對與鋼軌的豎向位移相同;(6)忽略構架點頭運動及輪對側滾和搖頭運動。這樣，每個車體具有橫擺、沉浮、側滾、點頭、搖頭等5個方向的自由度;每個轉向架有橫擺、沉浮、測滾、搖頭等4個方向的自由度;每個輪對具有橫擺和搖頭2個方向的自由度。因此每節車輛共有21個自由度。

2.2 橋梁模型

在建立橋梁有限元分析模型時，按結構實際情況對上下弦桿、腹桿、上下平聯、橋門架、拱肋，吊桿等桿件進行離散，采用空間梁單元模擬。橋梁橋墩亦采用空間梁單元進行模擬。

橋面槽形梁采用梁格法進行建模［9－10］。槽形梁是一種復雜的空間板梁組合結構，在結構受力上，槽形梁作為一種下承式預應力混凝土結構，具有開口薄壁構件受扭性能差、主梁腹板受力與橋面板及橫梁連接構造復雜、橋面板彎矩受主梁的扭轉剛度影響較大、主梁腹板下端承受垂直方向拉力影響較大等特點，與普通梁、板結構的受力情況有很大差異。故在建立橋面槽形梁模型時用普通梁、板單元模擬都不太合適，而用塊體單元則易導致模型單元數目巨大而致使計算效率過于低下。故選用適用于模擬板式、梁板式、箱梁上部結構及各種組合體系橋梁的梁格法來進行建模。梁格法的基本思路是把分散在板的每一區段內的彎曲和抗扭剛度都假定集中于最鄰近的梁格內。板的縱向剛度集中于縱向梁格內，橫向剛度集中于橫向梁格內，即用梁格等效原橋梁上部結構。梁格法的顯著優點是易于理解和使用，節省計算機內存，計算速度較實體單元和板殼單元法快，計算精度滿足工程要求，且能考慮梁體整個截面的橫向變形，特別適用于寬跨比較大的梁體。槽形梁的空間梁格模型采用空間梁單元，每個節點有6個自由度。根據槽形梁的結構特點，本文建立的空間梁格模型中以順橋向為y軸，豎橋向為z軸，橫橋向為x軸建立有限元模型。梁格模型的建立首先對槽形梁結構進行離散，將其沿順橋方向劃分成13根縱梁S1～S13，另在行車線的位置設a和b2根虛梁。各縱梁的截面特性值由軟件自帶的截面特性計算器算得。全模型節點214個，梁單元374個。其梁格截面劃分形式以及模型如圖2所示。

全橋的約束情況同連續梁，縱向限位支座設在中跨，每個橋墩均設一個橫向約束。彈性模量E和泊松比μ按現行橋規取值。對于橋面二期恒載，則將其作為均布質量分配到橋面槽形梁格體系的縱橫梁上。槽形梁通過支座支撐在鋼桁架的橫梁上，支座采用EBP彈性支座，支座剛度采用動力剛度值，邊支座動剛度為480 kN/mm;中支座的動剛度為800 kN/mm。

圖2 空間梁格模型縱梁截面劃分示意圖Fig.2 Schematic diagram of space beam gird model

2.3 列車－橋梁耦合振動方程的建立及求解

將橋梁及橋上列車視為整體系統。考慮各車輛與橋梁空間振動位移的相互關系，計算任意時刻t的橋上列車及橋跨空間振動的彈性總勢能。由勢能駐值原理［1］及形成矩陣的“對號人座”法則［7］，建立t時刻此系統的空間振動矩陣方程:

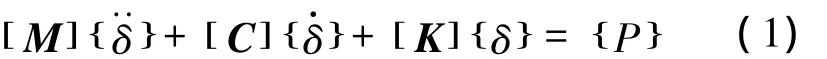
式中，{·δ·} ，{·δ}，{δ}分別為車橋系統在t時刻的加速度、速度、位移參數列陣。矩陣方程式(1)只考慮了列車重力作用，還不能求解，必須將車輛構架實測蛇行波(確定性分析)、構架人工蛇行波(隨機性分析)及軌道豎向不平順代入矩陣方程式(1)，按已知和未知位移參數進行矩陣分塊運算，導出包括車輛蛇行、軌道不平順等荷載項的系統空間振動微分方程組。然后按Wilson－θ法求得系統t時刻的振動響應。求解方程時以恒載下成橋狀態作為初始平衡狀態。

3 計算結果分析

3.1 橋梁自振特性分析

橋梁的自振頻率及振型特點反映了橋梁的剛度及橋梁的動力特性，是車橋振動響應分析的基礎。采用前面建立的動力分析模型對橋梁的自振特性進行計算分析，結果見表1。從表1可以看出:第1階自振頻率為橫向彎曲，表明該橋的橫向剛度相對較小，這和主梁的橫向剛度有關;由于拱肋提高了橋梁的豎向剛度，使橋梁的豎彎振型出現較晚。

表1 前5階自振頻率及相應振型Table 1 First five order of the natural frequency and vibration mode

3.2 車橋耦合振動計算結果

進行車橋耦合振動計算分析時，選用德國ICE列車，采用的列車編組為“2x(動車+動車+拖車+動車+動車+拖車+動車+動車)”，計算速度為160～350 km/h，分單、雙線行車。德國高速線路不平順譜密度是目前歐洲鐵路統一采用的譜密度函數，也是我國高速列車總體技術條件中建議的進行列車平穩性分析時所采用的譜密度函數。本文計算所采用的軌道不平順函數為德國低干擾譜。計算中采用不平順樣本序列全長2 000 m，不平順測點間距0.25 m高低不平順的幅值為7.59 mm，軌向不平順的幅值為5.5 mm，水平不平順的幅值為3.95 mm。計算得到的橋梁和車輛振動響應結果分別見表2～表4，為簡便起見，表中各項響應均只給出最大值。表中，Q/P和△P/P分別表示脫軌系數、輪重減載率;AV和AL分別表示心盤豎向、橫向振動加速度;WZV和WZL分別表示斯佩林舒適度豎向、橫向指標。其中表2的橋梁振動位移值均為相對于初始平衡位置而言。

表2 橋梁動力響應最大值Table 2 Maximum dynamic response of bridge

表3 機車動力響應值Table 3 Maximum dynamic response of locomotive

表4 車輛動力響應值Table 4 Maximum dynamic response of cars

從計算結果可以看出:

(1)橋梁、車輛的振動響應在總體上有隨著列車運行速度的提高而增大的趨勢;

(2)對比列車單線行車與雙線對開的車橋響應計算結果，可看到:雙線對開時的橋梁動撓度和跨中豎向振動加速度比單線行車增大較多，其余相差不大，但雙線對開時的響應值略大;

(3)該橋梁方案在ICE高速列車以速度160～350 km/h運行時，沖擊系數最大值為1.07;橋梁跨中截面最大豎向撓度18.0 mm大約為跨徑的1/11 000;最大橫向位移1.15 mm，相應橫向撓跨比很小。

3.3 列車運行安全性和舒適性的評判

采用脫軌系數、輪重減載率來判斷列車運行安全性，用斯佩林(Sperling)指標判斷乘坐舒適性(或運行平穩性)。根據《鐵道機車動力學性能試驗鑒定方法及評定標準TB/T2360－93》、《鐵道車輛動力學性能評定和試驗鑒定規范GB5599－85》，并參考歷次提速試驗所采用的評判標準，在車橋動力仿真分析中，列車運行安全性與 舒適性(平穩性)的評定指標選取如下:

(1)安全性評定指標

脫軌系數:≤0.8;輪重減載率:≤0.6

(2)乘坐舒適性評定指標(對客車車輛)

車體振動加速度:豎向 ≤ 0.25g;橫向 ≤0.20g(中速:≤200 km/h)

豎向 ≤ 0.13g;橫向 ≤ 0.10g(高速:≥ 200 km/h)

舒適性評價指標:優良 ＜2.50

良好 2.50 ～ 2.75

合格 2.75 ～ 3.00

(3)運行平穩性(對貨車車輛)

車體振動加速度:≤ 0.70g=7.0 m/s2(半峰值，豎向)

≤ 0.50g=5.0 m/s2(半峰值，橫向)

平穩性評價指標:優良 ＜3.50

良好 3.50 ～ 4.00

合格 4.00 ～ 4.25

(4)機車運行平穩性

車體振動加速度:≤ 0.365g=3.65 m/s2(半峰值，豎向)

≤ 0.245g=2.45 m/s2(半峰值，橫向)

平穩性評價指標:優良 ＜2.75

良好 2.75 ～ 3.10

合格 3.10 ～ 3.45

(5)橋梁動力響應限值

1)橋梁豎向振動加速度限值:0.35g=3.5 m/s2(半幅、有碴軌道)。

0.50g=5.0 m/s2(半幅、無碴軌道)。

2)橋梁橫向振動加速度限值:0.15g=1.5 m/s2(半幅)。

從計算結果可以得到:

(1)ICE高速列車以速度160～250 km/h通過橋梁時，機車車輛脫軌系數最大值為0.28，小于0.8，輪重鍵載率最大值為0.19，小于0.6;ICE高速列車以速度270～350 km/h通過橋梁時，機車車輛脫軌系數最大值為0.43，小于0.8，輪重鍵載率最大值為0.42，小于0.6。因此，列車行車時的安全性可以得到保障。

(2)該橋梁方案在ICE高速列車以速度160～250 km/h運行時，機車車輛的豎向舒適性為優良，橫向舒適性亦為優良;速度為270～350 km/h時，機車車輛的豎向舒適性為良好，橫向舒適性為良好。車輛豎向、橫向加速度最大值均在限值以內。

(3)該橋梁方案在ICE高速列車以速度160～350 km/h運行時，橋梁主跨跨中截面最大豎向動撓度、最大橫向振動位移均較小，豎向、橫向振動加速度最大值均在限值以內，高速列車通過時引起的橋梁振動較小。

4 結論

(1)目前關于橋梁剛度標準的國內外相關規范均不適用于大跨度拱橋，運用橋梁結構動力學與車輛動力學的研究方法將車橋作為聯合動力體系，建立了高速列車與大跨度拱橋的車橋耦合動力分析模型，其中針對橋面槽形梁的特點運用了梁格法建模。

(2)ICE列車通過橋梁時，橋梁的最大橫、豎向動位移及振動加速度均較小，表明該設計方案橋梁的橫、豎向剛度均較大。

(3)隨著列車運行速度的提高，列車的振動響應從總體上來說呈現逐步增大的趨勢，但其最大脫軌系數、最大輪重減載率及車體振動加速度均小于相應限值，因此列車的運行安全性滿足要求，列車的橫、豎向乘坐舒適度均達到良好及以上標準。

(4)橋面采用槽形梁結構形式的大跨度鋼桁拱橋具有良好的動力特性及列車走行性，鋼橋采用這種形式的橋面是可行的。

［1］曾慶元，郭向榮.列車橋梁時變系統振動分析理論與應用［M］.北京:中國鐵道出版社，1999.ZENG Qing-yuan，GUO Xiang-rong.Theory and application of train－bridge time－variant system vibration analysis［M］.Beijing:China Railway Press，1999.

［2］陸光閭.連續鐵路槽形梁橋空間作用分析［J］.鐵道學報，2000，22(zl):41 －45.LU Guang-lu.Spatial analysis of railway continuous through girder bridge［J］.Journal of The China Railway Society，2000，22(zl):41 －45.

［3］賀恩懷.槽形梁在城市軌道交通工程中的應用［J］.城市軌道交通研究，2003，6(3):68－70.He Huai－en.The application of mould beam in urban rail traffic engineering［J］.Urban Mass Transit，2003，6(3):68－70.

［4］奚岱銘，張寧勇.軌道交通高架上部結構型式的分析與探討［J］.中國市政工程，2005(1):24－26.XI Dai-ming，ZHANG Ning-yong.Analysis ＆ discussion on superstructure types of rail traffic viaducts［J］.China Municipal Engineering，2005(1):24－26.

［5］夏 禾，張 楠，張鴻儒，DE ROECK Guido.300 km/h高速鐵路 PC槽形梁動力試驗研究［J］.工程力學，2003，20(6):99 －105.XIA He，ZHANG Nan，ZHANG Hong － ru，DE ROECK Guido.Experimental study of a prestressed trough bridge for high speed railway［J］.Engineering Mechanics，2003，20(6):99－105.

［6］李 麗，王振領，張宇寧.地鐵高架槽形梁足尺模型破壞試驗與空間分析研究［J］.中國鐵道科學，2005，26(5):31－35.LI Li，WANG Zhen-ling，ZHANG Yu-ning.Fracture load test and spatial analysis for the full scale model of underground viaduct channel girder［J］.China Raiway Science，2005，26(5):31 －35.

［7］曾慶元，楊 平.形成矩陣的“對號入座”法則與桁段有限元法［J］.鐵道學報，1986，8(2):48－59.ZENG Qing-yuan，YANG Ping.The“set－in－rightposition”rule for formulation matrix and the truss finite element method for spatial truss analysis［J］.Journal of the Railway Society，1986，8(2):48 －59.

［8］曾慶元.列車－橋梁時變系統的橫向振動分析［J］.鐵道學報，1991，13(2):31 －37.ZENGQing-yuan.Train－bridge time－variant system lateral vibration analysis［J］.Journal of the Railway Society，1991，13(2):31 －37.

［9］羅靜峰，田楊.梁格法在彎箱梁橋結構分析中的應用［J］.鐵道標準設計，2010(3):77 －79.LUO Jing-feng，TIAN Yang.Application of beam grillage method in analysis on structure of curved box beams［J］.Railway Standard Design，2010(3):77－79.

［10］戴公連，李德建.橋梁結構空間分析設計方法與應用［M］.北京:人民交通出版社，2001.DAI Gong-lian，LI De-jian.Design method and application of bridge structure space analysis［M］.Beijing:China Communications Press，2001.