可列個無窮小積的極限的存在性分析

楊 挺

可列個無窮小積的極限的存在性分析

楊 挺

摘 要：文章辨析了“可列個無窮小的積一定是無窮小”這一結論中的疑義，應用二重極限的概念分析了產生這一問題的原因，在構造了兩個反例的基礎上，給出了這一命題成立的兩個充分條件。

關鍵詞：教學研究；高等數學；無窮小；可列積；充分條件

楊挺/連云港體育運動學校講師（江蘇連云港222000）。

無窮小是極限理論中的重要概念，通常在教材中把無窮小與無窮大兩個內容合并列為一個小節，并把無窮小的階的比較進行研究和討論，由此可見其重要性。在講述無窮小概念的時候，直接給出下面的定理。

定理1 無窮小與有限函數的乘積是無窮小。

定理2 有限個無窮小的和是無窮小。

定理3 有限個無窮小的積是無窮小。

前兩個定理都容易理解，對于定理3，無窮多個無窮小的乘積是什么呢？難道可能不是無窮小嗎？幾乎每年都有學生會提出這樣的問題，而且難以解釋清楚。實際上，在教師中也常常會存在著這樣的疑問。

一、錯誤起因

理解的錯誤產生于數學歸納法的應用。

例1 用數學歸納法證明：無窮多個無窮小的乘積是無窮小。

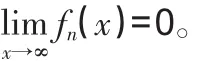
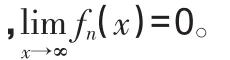
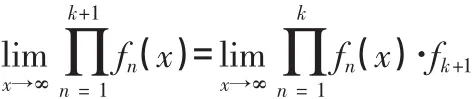
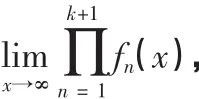
正是由于例1的證明，很多人錯誤地認為：可列個無窮小的乘積必是無窮小。不幸的是，此證明過程是錯誤的，其根源在于忽略了無窮小結構本身的特殊性和二重極限的復雜性。

二、錯誤辨析

實際上，對此命題正確性的討論最好是在學生學習過二重極限之后，此時學生的認知水平、知識儲備達到一定程度才能真正理解和掌握。

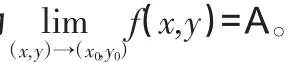
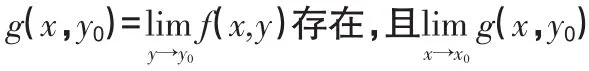
由定義1和定義2，類似可定義函數f（x,y）在無窮遠點處的二重極限，以及先對x再對y的二次極限。

對于二重極限與二次極限的關系，以下三個結論是共知的：

函數的二重極限存在，兩個二次極限不一定存在，即使二次極限都存在也不一定相等。

函數的兩個二次極限都存在且相等，二重極限不一定存在。

函數的兩個二次極限不一定都存在。

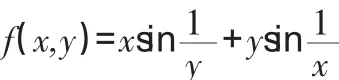
1.函數的情形。這里討論自變量x→∞時的函數無窮小序列的情形，其它自變量變化過程可類似分析。

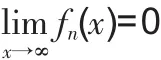
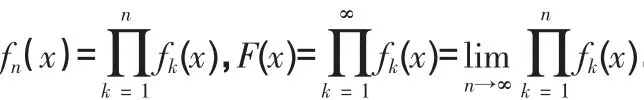
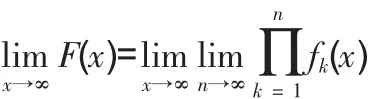
是否為0。

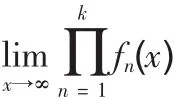
2.數列的情形。

三、兩個實例

上述兩個例題說明了當函數值（數列值）由兩個變量決定時，可列個無窮小的乘積可能不是無窮小，進一步的，當決定數值的變量更多時，其變化形式將更加復雜，可列個無窮小的乘積不是無窮小的實例將更多。

四、可列個無窮小的乘積是無窮小的充分條件

產生上述問題的主要根源在于，在變量變化過程中，函數值可能會受到多個變量的影響，任意一個變量都不可能決定函數的取值及變化趨勢。

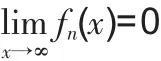
仿此可定義x→x0時及其它自變量變化過程時的一致無窮小函數序列，也可以類似定義一致無窮小數列序列。

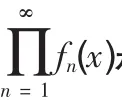
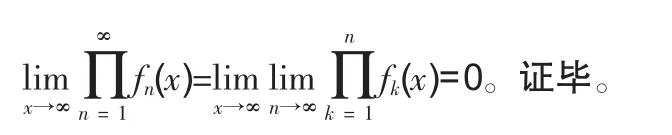
證明：對任意的 ε＞0，存在 M＞0（M與 n無關），使得當 |x|＞M時，恒有 |fn(x)|＜ε，因此不妨設 ε＜1，則有

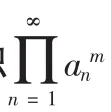
推論2數列{anm|n=1,2，Λ}是無窮小數列序列，且單調遞減，則其可列積

證明類似于定理1，略。

由定理1和定理2以及函數極限存在的充要條件，可得如下推論：

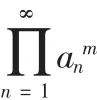
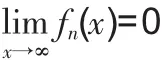
推論2的證明略。

中圖分類號：O171

A

1671-6531（2012）11-0033-02

：姚 旺