基于多重多元回歸的木材干燥質量預測模型

丁徽 謝健 段文英

(東北林業大學，哈爾濱，150040)

多重多元回歸分析是回歸分析的一個重要分支，是多個因變量與多個自變量間的回歸分析，具有一般性和廣泛性，能更好地解決實際中的諸多問題。如生物和環境問題、生物系統中的功能團之間的關系等[1]。

木材干燥過程中的應力和含水率是木材干燥重要的質量指標。木材干燥過程中，影響干燥質量的因素分別為外部因子和內部因子。外部因子包括介質的溫度，相對濕度、壓力及通過材面的氣流速度。內部因子主要是樹種，木料厚度和含水率等。木材干燥過程中，內部因子是不能控制的，只能通過外部因子的控制來達到提高干燥質量的最終目的。壓力和氣流速度，在干燥設備安裝完畢后，一般都已固定，所以也不在考查范圍內。實驗室中干燥溫度可以直接由干球溫度確定，相對濕度可以由平衡含水率代替[2－3]。本研究選取干燥過程中的干燥溫度、干燥濕度、干燥時間作為自變量，來預測含水率及應力的變化。這類多個質量指標與其影響因子間的關系問題適用于選擇多重多元回歸分析方法。

1 多重多元回歸分析的基本原理

1.1 多重多元回歸分析的數學模型

設有m個自變量x1，x2，…，xm對應p個因變量y1，y2，…，yp，假定它們有線性關系式:

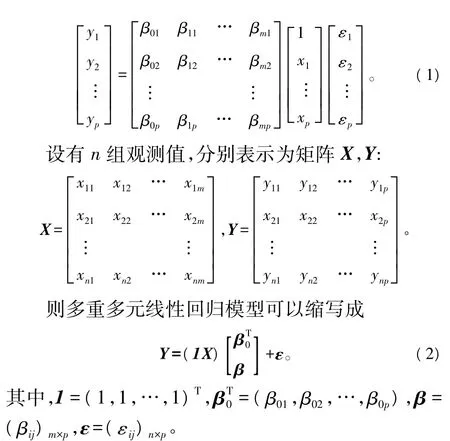
n＞m+1，R(1X)=m+1，ε 為殘差的各行向量相互獨立，且同分布N(0，∑)。

1.2 多重多元回歸分析模型的檢驗

在得到回歸模型之后，并不能直接拿來做預測，必須進一步診斷所得的模型是否符合之前做的假設，所以需要對回歸模型進行診斷。首先，最直觀的診斷就是進行殘差分析。由于之前的假設均是在正態分布的前提下，所以通過殘差圖來初步診斷模型的正確性。選用學生化殘差，其中。稱為杠桿值 用學生化殘差作為縱坐標，擬合值^y為橫坐標作殘差圖。學生化殘差在[－3，3]中，并且學生化殘差與擬合值之間不呈現任何相關關系，即可初步認定模型的正確性[4－5]。再對模型的顯著性進行檢驗，判定模型的擬合效果。使用SAS8.1軟件進行數據處理回歸分析[6]。

2 基于多重多元回歸的木材干燥應力、含水率預測模型

2.1 數據獲取

本研究所采用的數據均來自東北林業大學木材干燥實驗室。實驗選用材是俄羅斯進口落葉松(Larix gmelinii)鋸材，其規格為4000 mm(長)×100 mm(寬)×30 mm(厚)。試材平均初含水率在50%左右。選取干燥階段的數據進行分析。干燥24 h之后，每隔6 h進行一次含水率、應力的實驗板檢測，計算出應力指標和含水率，同時測定干球溫度、平衡含水率，記錄干燥時間。實驗共收集21組數據，剔除4組錯誤數據，共17組數據。

2.2 數學模型的建立

選取干燥過程中的干燥應力(y1)、含水率(y2)作為因變量，干燥溫度(x1)、干燥濕度(x2)、干燥時間(x3)作為自變量，在不考慮其他影響因素的條件下，假設它們間存在線性關系，建立應力和含水率的預測模型。

首先對應力和含水率進行正態性檢驗，如圖1。應力、含水率大致服從正態分布，證明進行多重多元回歸的必要條件是具備的。

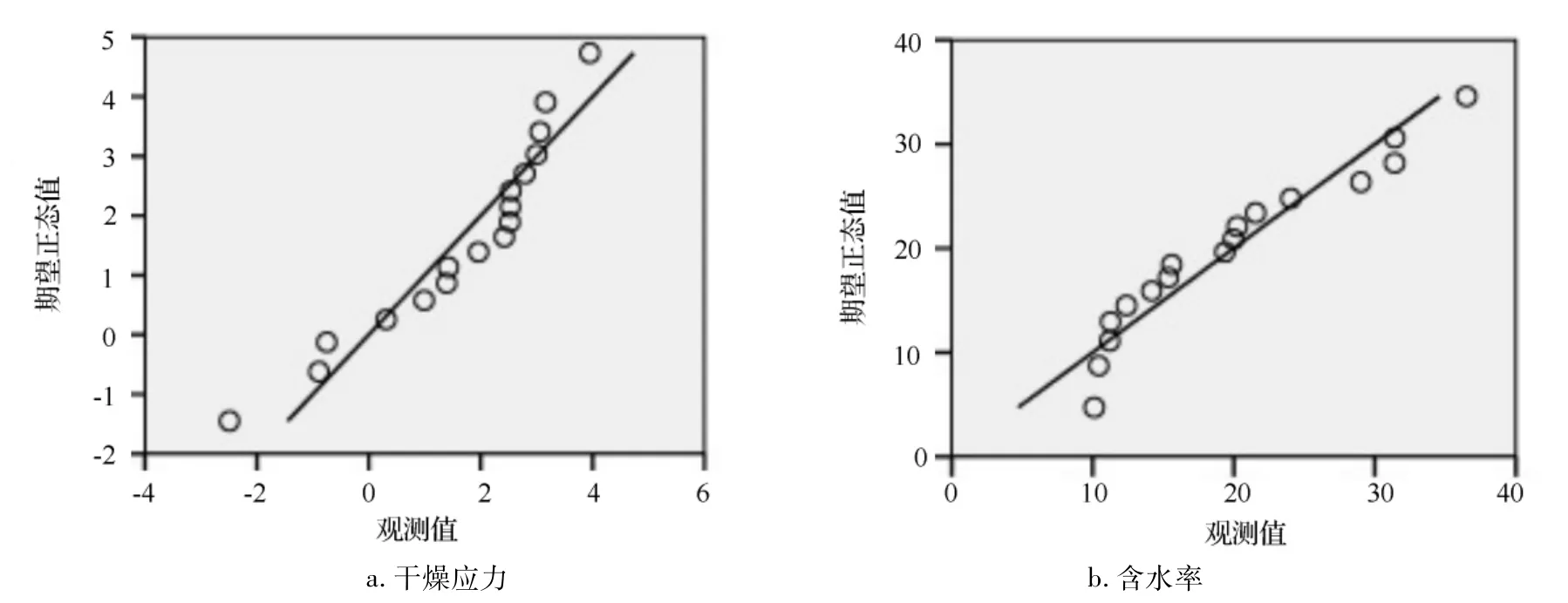
圖1 木材干燥應力、含水率的正態檢驗

根據實驗所測的的數據，建立如下干燥應力和含水率的多重多元回歸預測模型:

2.3 模型的檢驗

干燥應力和含水率的觀測值與預測值之間的殘差也大致接近正態分布，如圖2。

另外，學生化殘差與預測值之間不呈現某種特殊的關系，如圖3，即殘差沒有隨干燥應力和含水率預測值的變化而變化，這樣就初步認定模型的正確性。

表1給出了應力和含水率的預測模型檢驗。兩個方程均滿足F檢驗，其中含水率的預測方程顯現出較大的 F 值，均大于臨界值(F0.05(3，13=3.41)，證明方程十分顯著。應力和含水率的的R2(擬合優度)值分別為93.00%、99.83%。證明模型的擬合效果還是比較好的，對實際預測具有重要意義。

3 結論

利用多重多元回歸分析方法建模，將木材干燥指標作為一個整體，建立干燥影響因素對干燥質量的預測模型。給出了木材干燥質量指標含水率和應力的預測模型，該模型在木料厚度、初含水率、干燥設備均固定的條件下，根據溫度、相對濕度，干燥時間，可預測木材的含水率及應力。模型檢驗表明，預測方程的擬合度較高，具有較好的預測效果。對于其他樹種可以用類似方法構建模型。這對在線預測干燥應力、含水率，提高干燥過程控制水平具有較為重要的現實意義。

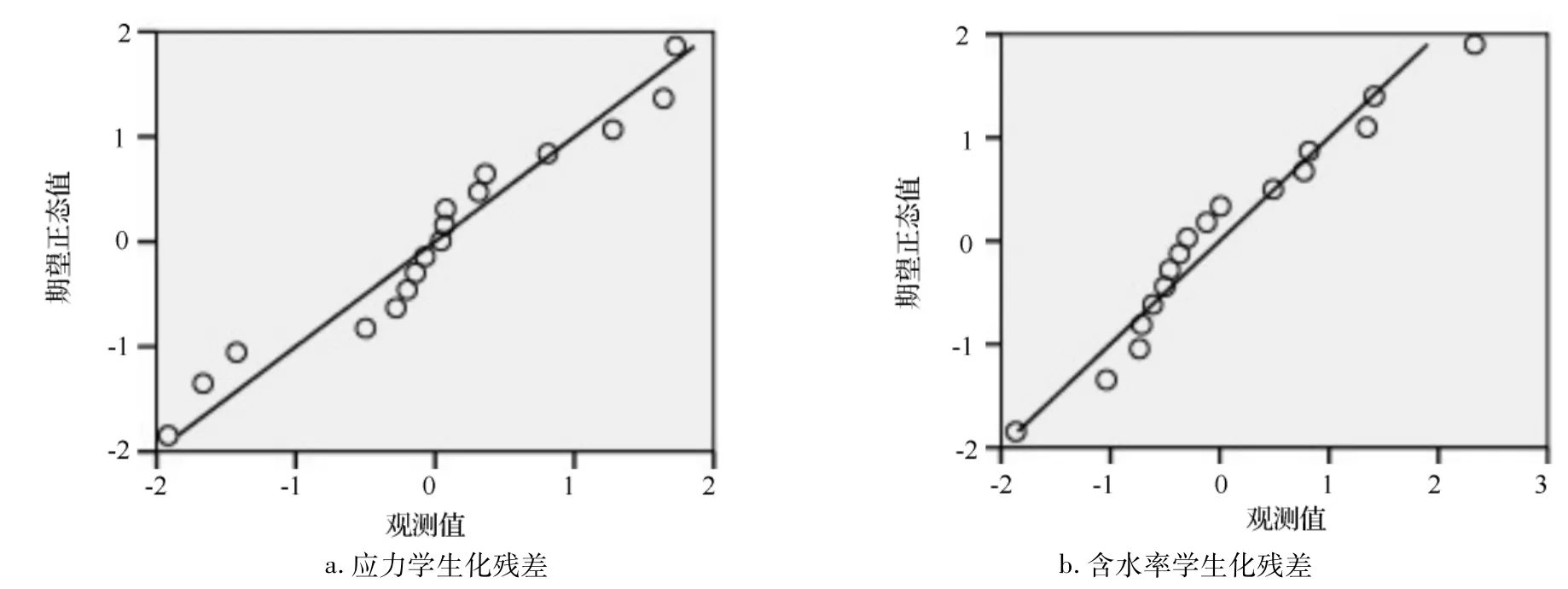
圖2 應力、含水率殘差的正態性檢驗

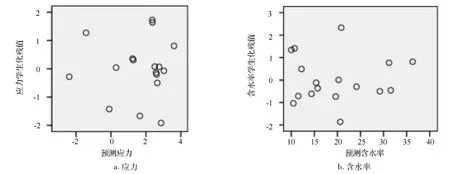
圖3 應力、含水率殘差與預測值的關系

表1 回歸模型的顯著性檢驗

[1]袁志發，宋世德.多元統計分析[M].北京:科學出版社，2009:170－175.

[2]張冬妍.木材干燥神經網絡建模與智能控制研究[D].哈爾濱:東北林業大學，2005:1－3.

[3]張璧光.實用木材干燥技術[M].北京:化學工業出版社，2005:158－159.

[4]何曉群，劉文卿.應用回歸分析[M].2版.北京:中國人民大學出版社，2007:44－47.

[5]吳喜之，田茂再.現代回歸模型診斷[M].北京:中國統計出版社，2003:7－9.

[6]阮桂海，蔡建平，建瓴，等.SAS統計分析實用大全[M].北京:清華大學出版社，2003:188－210.