確定飛機最大抖振設計載荷的長期極值估計方法

李 斌，張玉杰，楊智春

(西北工業大學 航空學院，西安 710072)

抖振是現代雙垂尾戰斗機［1］(大攻角機動引起旋渦破裂)和特種電子作戰飛機(外加電線類凸起物引起氣流分離)在服役過程中經常要遭遇的復雜動載荷環境，屬于典型氣彈響應問題。因此對于這類飛機在設計過程必須精細考慮其抖振載荷對結構安全的影響。在現代飛機結構設計中，振動嚴重部位的動態設計載荷的確定要求合理確定振動過程中的可能最大響應、并估計最大響應對應的最大內力載荷。尤其對于具有不確定特性的隨機振動過程，如何根據有限的測試或計算樣本數據，恰當地估計最大動態設計載荷，則顯得更為重要。

飛機設計的工程實踐中，在隨機振動工況下，確定動態設計載荷的傳統習慣方法是采用所謂的3σ法則，其中σ指振動響應的均方根值。該法則的數學內涵為，Gauss隨機變量在(－3σ，3σ)區間外取值的概率為0.27%。但實際飛機設計中對限制載荷的定義是服役中預期的最大載荷［2］。很顯然3σ法則確定的極值載荷一般是不滿足限制載荷定義的。但是在飛機沒有服役之前，缺乏安全使用壽命飛行數據的條件下，難以直接得到最大載荷峰值，只能根據有限的計算數據或風洞試驗數據，采用預估方法進行估計可能出現的載荷最大值。目前在飛機設計過程，可供參考的一類確定動態載荷峰值的方法是根據指定的超越次數指標來截取極限載荷。如對突風載荷設計，Hoblit［3］推薦的限制設計超越次數是2×10－5次/飛行小時。這種基于設計超越次數指標的抖振載荷設計方法在F－22飛機完成試飛測試，獲得大量抖振試飛數據后也得到了應用。文獻［4］給出的確定極限載荷的可接受超越指標為全壽命周期內107次飛行發生一次，或超越概率為1×10－4。但這種方法應用的前提是必須先建立飛機全壽命周期的抖振載荷超越曲線，這對于設計階段的抖振載荷預估確定來說難以滿足。

確定設計階段的抖振最大設計載荷，可以利用的數據有:縮比模型的風洞試驗數據和抖振響應計算數據。這兩種參考數據均只是有限長度，不可能覆蓋全壽命周期。因此，有必要建立一種可靠的統計預測方法，利用短時間段內的響應數據，來預測飛機全服役時間內可能發生的最大抖振載荷。極值估計理論是解決這類問題的有效手段之一［5］，目前已經在土木結構的風工程研究領域得到較為廣泛的應用［6］。本文結合某型飛機尾部結構的抖振風洞試驗數據，運用次序統計和極值估計理論，基于極值I型分布和III型分布，分別應用線性的最小二乘估計和最大似然估計進行極值模型的參數估計，并根據預設極值重現期指標進行抖振響應數據的極值估計。此外，通過不同分析方法的對比，闡明了傳統的3σ法則的局限性，并給出了應用極值估計理論確定動態設計載荷時的若干建議。

1 極值估計理論

用X1，X2，…，Xn代表n個獨立的樣本，x是任意樣本Xi的最大絕對值，在大樣本數目的條件下，Gumbel給出了x的三種漸近分布。這三種分布可以統一用廣義極值分布函數表示:

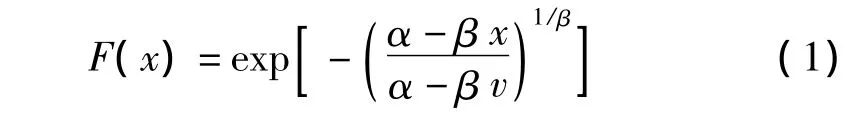
式中，β=0稱為極值Ⅰ型分布，實際是一種雙參數分布函數;β＜0表示極值Ⅱ型分布;β＞0表示極值Ⅲ型分布。后兩種都屬于三參數分布函數，分布函數的尾部較長。參數α，β，v具有確定的物理含義。β稱為形狀參數，確定極值分布函數的形狀;v為位置參數，表示最頻繁發生的極值水平，對應分布密度函數的中心峰值位置;α為尺度參數，表示極值水平隨對數時間變量的增長率;α/β則表示可能發生的極值。實際應用過程中，極值Ⅱ型或Ⅲ型分布的適用性由估計形狀參數β決定。

在極值估計中，重現期是一個非常重要的概念，假定單個樣本數據占據的物理時間長度為Δt，則重現期的數學表達式為:

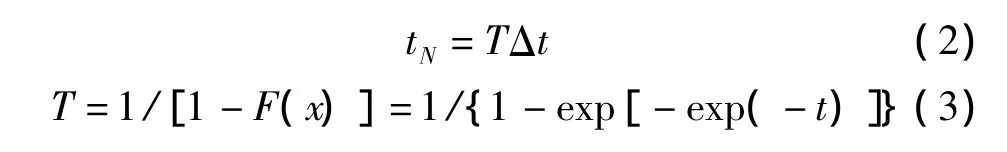
式中，t稱為對數減縮變量，t= －lnln［1/F(x)］。重現期tN的物理意義是觀察到等于或大于x的極值所需的操作時間長度。1－F(x)表示超越概率。

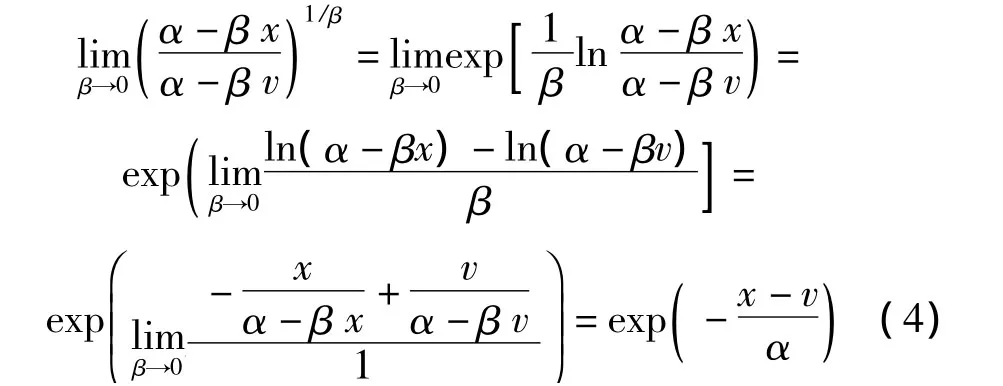
將式(4)代入式(1)可得I型分布函數的表達式為:

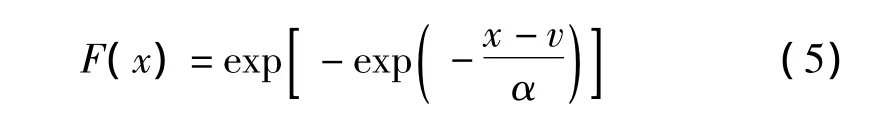
比較式(1)和式(5)，可以發現，Ⅰ型分布屬于雙參數分布，估計方便，計算簡單，而且對取值無上下限要求。Ⅲ型分布屬于三參數分布，可估計的數據類型較廣，能夠有效地彌補Ⅰ型分布的缺陷。

2 參數估計方法

2.1 基于經驗分布假設的最小二乘估計法

對于Ⅰ型分布，x的總體分布函數如式(5)所示。引入變量:

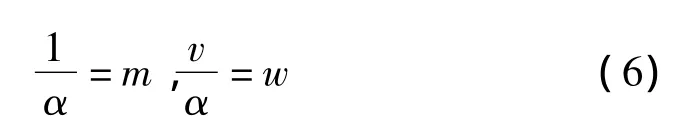
則式(5)可化為:

將式(7)代入式(3)，推導出x－T關系式:

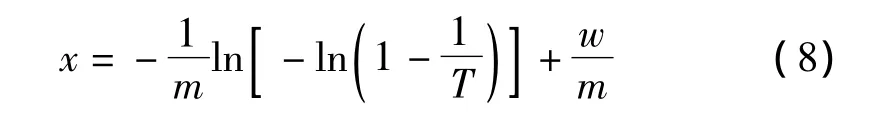
或x－t關系式:

對于Ⅲ型分布，x的總體分布函數如式(1)所示。引入變量:

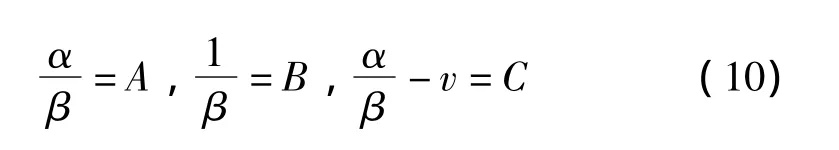
則式(1)可化為:

將式(11)代入式(3)推導出x－T關系式:

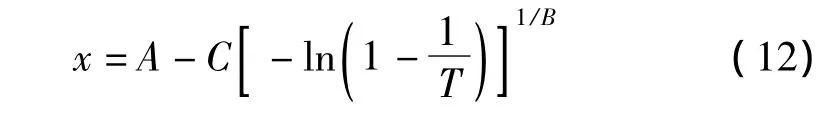
或x－t關系式:

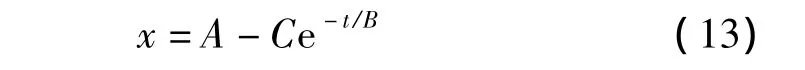
應用最小二乘法進行參數估計的一般步驟為:(1)將選定時間段內的數據分為n份，從每份中選取最大絕對值x;

(2)將這n個x值按從小到大順序排列;

(3)引入經驗分布函數，經過次序排列后的極值分布函數可以表示為:F(x)=i/n，或F(x)=i/(n+1)，i=1，2，…n。為避免F(x)=1時t無解的情況出現，一般取后者。引入t的定義，則t=－lnln［(n+1)/i］;

(4)對于Ⅰ型分布，考慮到式(9)，引入x關于t的線性表達式:x=at+b;對于Ⅲ型分布，考慮到式(13)，引入x關于t的指數表達式:x=DeEt+F;

(5)依據經驗分布函數，對應每一個級別x，可以計算得到對應的t，將它們代入到步驟(4)的參數方程，可以建立a，b或D，E，F為未知量的矛盾方程組，然后求解該矛盾方程組的最小二乘解。其中求解D，E，F的具體做法是，令d=eEt，根據d和x相關系數最大的原則確定E。當E確定后，就可由線性最小二乘法擬合D和F，詳細算法參考文獻［7］;

(6)將 a，b或 D，E，F的估計值分別回代到式(6)、式(10)中，可得參數 α，β，v的估計值。

2.2 最大似然估計法

下面用最大似然估計法分別導出Ⅰ型分布和Ⅲ型分布參數的計算公式。

對于如式(7)所示的Ⅰ型分布函數，分布密度為:

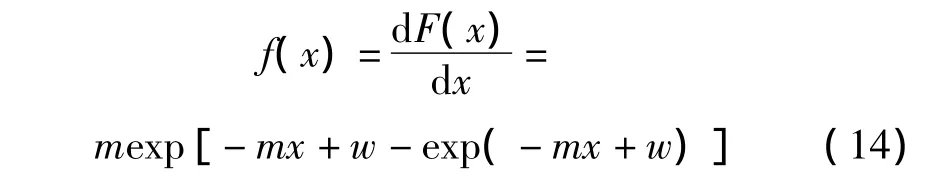
似然函數為:

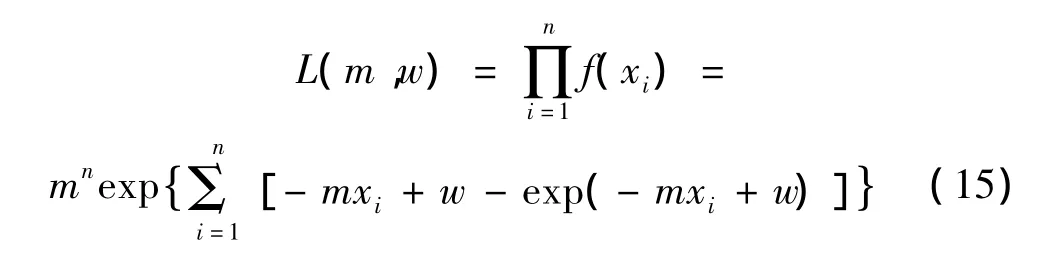
對式(15)兩邊取自然對數可得:

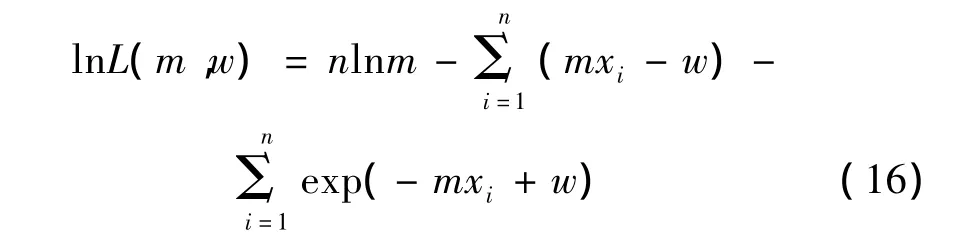
lnL(m，w)取極值的條件為:

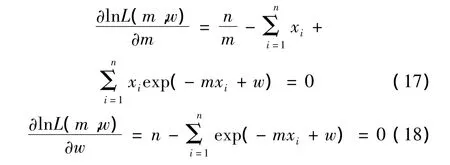
可以利用Gauss-Newton迭代法求解式(17)、(18)組合而成的以m，w為未知數的非線性方程組。本文具體計算時應用MATLAB自帶的非線性求解函數“lsqnonlin”進行求解。

對于如式(11)所示的Ⅲ型分布函數，它的分布密度為:

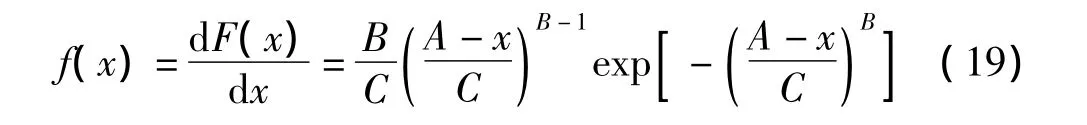
似然函數為:

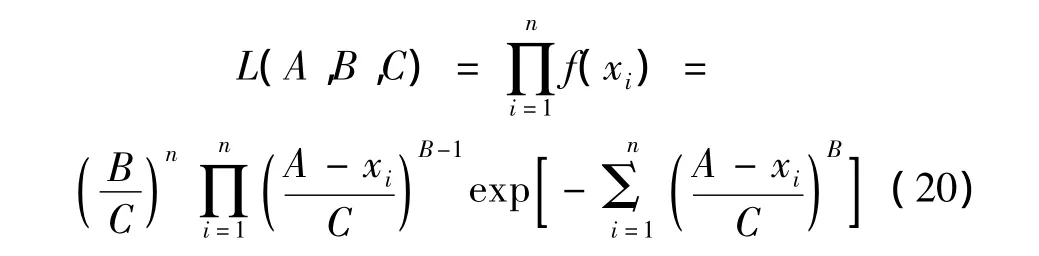
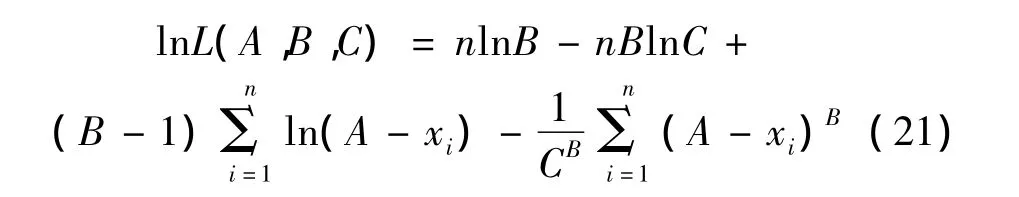
對式(20)兩邊取自然對數可得:

對 lnL(A，B，C)取極大值，得:

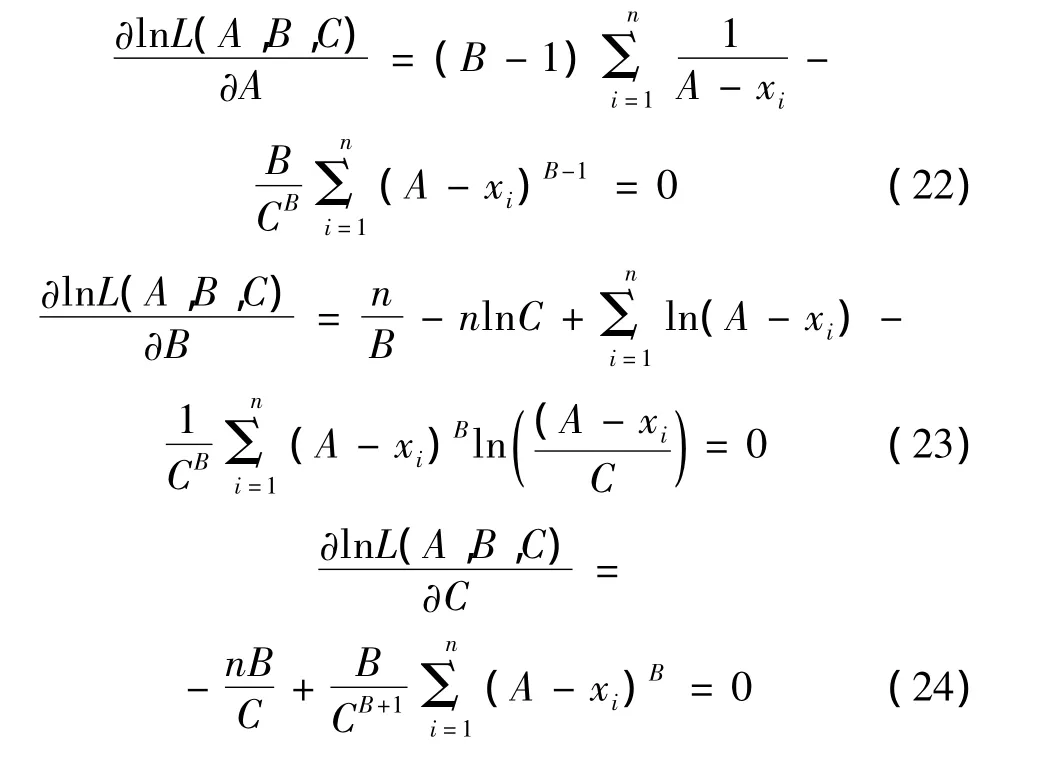
同樣可以利用Gauss-Newton迭代法求解式(22)、式(23)、式(24)組合而成的以A，B，C為未知數的非線性方程組。對于Ⅲ型分布，初值的選取顯著影響計算結果。參照文獻［7］，A，B，C 初值分別取為 1.5xn，5，1.5xn－0.4，其中，xn為數量為 n 的極值樣本中的最大值。

3 應用實例與分析

應用長期極值估計理論，可以建立振動響應極值大小與樣本數量(即重現期)之間的關系。實際設計中則可以通過給定重現期來求取對應的設計極值。例如在土木工程結構的設計規范中，確定結構風載荷時通常定義“幾十年”一遇的重現期。

對于飛機抖振設計載荷確定來說，重現期的確定可以遵循如圖1所示的流程框圖來預設。首先影響確定影響抖振響應烈度的敏感參數，并用敏感參數來進行典型狀態的劃分。然后按照飛機使用習慣，確定飛機的典型任務剖面。要求每個典型任務剖面內，每飛行小時各典型狀態的可能累積發生時間相對穩定。最后根據飛機的全壽命周期使用統計情況，將整個飛行壽命周期內的典型狀態可能發生的時間累加起來則可以得到對應的“典型狀態”的設計重現期。依據該重現期，則可進行設計載荷極值的估計。

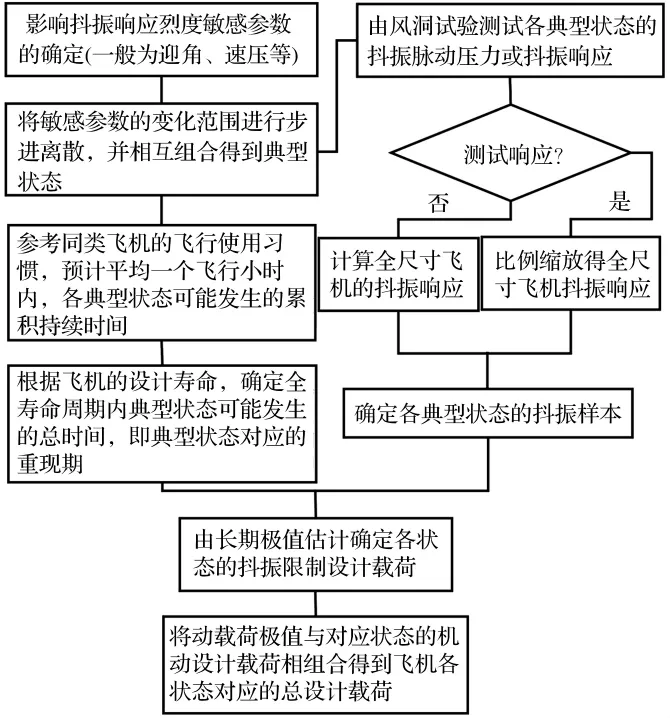
圖1 抖振設計載荷確定框圖Fig.1 Flow chart to determine buffet design load

下面以某型飛機尾部結構的抖振響應風洞試驗測試數據為例進行極值估計方法的實例討論。如圖2所示為通過風洞試驗獲得的某型飛機尾部結構的典型加速度振動響應數據，數據采樣頻率為2 048 Hz，采樣時間24 s。為了有利于統計模型的參數估計，對原始數據幅值進行了無量綱規范化處理，即將測試數據統一處理到±0.8的變化范圍內，Ca=對該數據進行正態分布檢驗，統計和擬合得到的概率密度曲線和分布曲線分別如圖3所示，可見響應數據符合正態分布假設，響應屬平穩隨機過程。

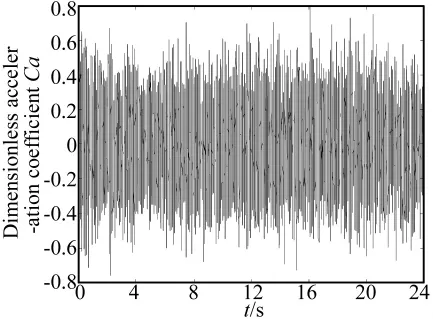
圖2 測試的抖振響應樣本Fig.2 Sample of measured buffet response data

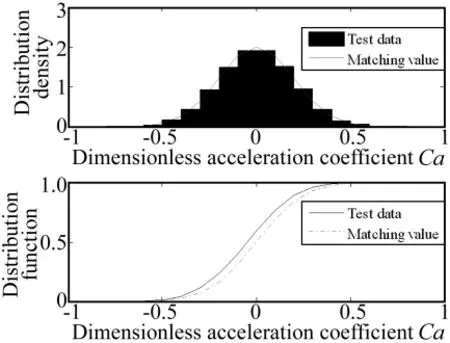
圖3 抖振數據正態分布檢驗Fig.3 Probability distribution check of buffet data

3.1 關于極值模型和估計方法的討論

為了檢驗極值估計模型和估計方法的適用性，以圖2所示的24 s長度的數據作為數據總體，根據前文對數據的規范化處理方法，可知其理想極值為0.8。以每128個時域測試數據作為一個樣本，則每個子樣本對應的時間長度Δt=0.062 5 s。提取各個子樣本內的極值(絕對值)，進行極值分布參數估計分析。應用第2節所述的最小二乘法和最大似然法分別進行極值Ⅰ型分布和Ⅲ型分布的參數估計，結果如表1和圖4所示。

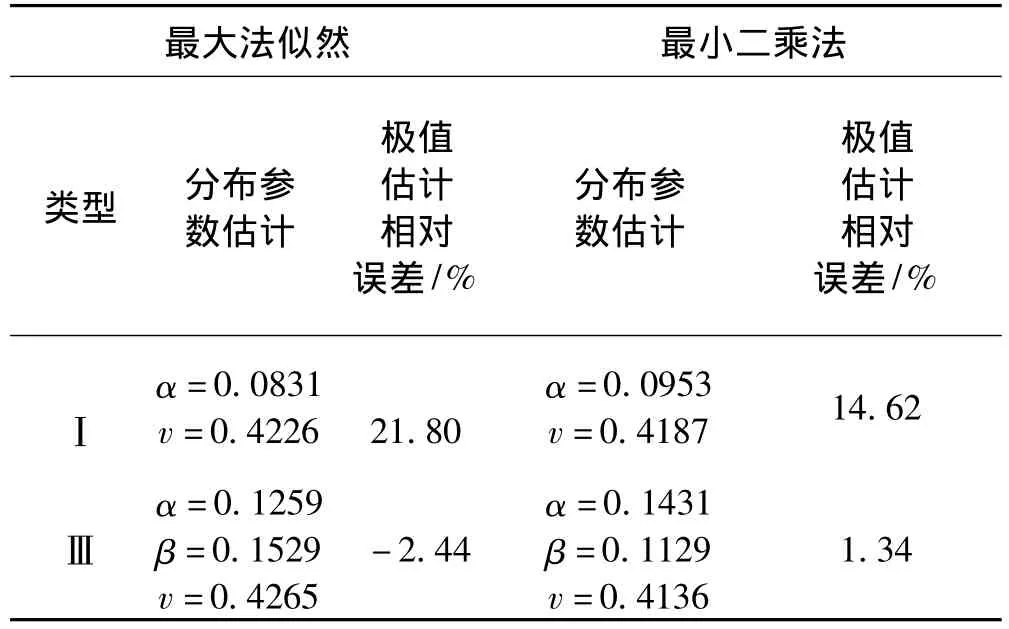
表1 Ⅰ型和Ⅲ型分布模型對比Tab.1 Comparison betweenⅠ andⅢ distribution model

觀察表1可以發現，無論采用最小二乘法還是最大似然估計法，Ⅰ型分布估計出來的極值偏差都比實際值大14%以上，過于保守。Ⅲ型分布估計得到的最大抖振載荷更接近實際值，圖4中兩種模型得到的極值估計曲線與試驗數據統計曲線的對比也說明了這一點，Ⅰ型分布估計在初始階段與實際統計曲線吻合較好，但隨著對數減縮時間變量的增長，曲線后段的偏離越來越大。導致這種現象的主要原因是雙參數模型較難描述長尾分布。如圖5所示為超越概率分布曲線，Ⅲ型分布模型明顯改善了曲線后段的描述精度，擬合后的總體趨勢曲線與實際統計數據之間的吻合性非常好。

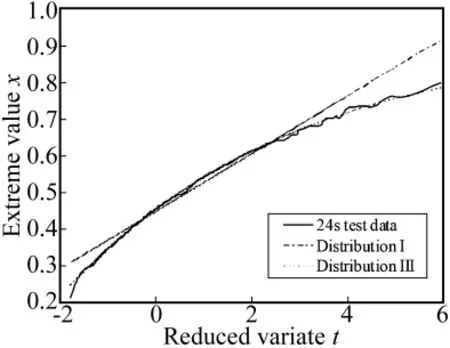
圖4 Ⅰ型和Ⅲ型分布估計值和試驗值的對比Fig.4 Comparison of measured and predicted extreme value using distributionⅠandⅢ

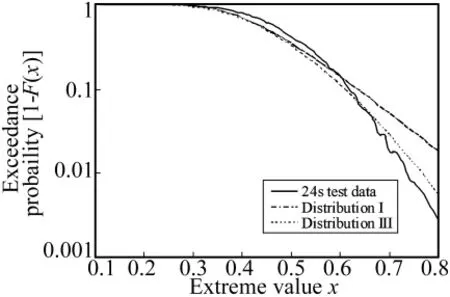
圖5 超越概率分布曲線對比Fig.5 Comparison of measured and predicted exceedance probability using distributionⅠandⅢ

表2進一步采用抖振風洞試驗中獲得的10組不同的24 s長度的測試數據，基于Ⅲ型分布，分別應用最小二乘法和最大似然估計法進行了載荷極值估計，估計結果如表2所示。對比分析各組數據表明，應用最小二乘法估計出來的最大抖振響應值較試驗值略低，屬于偏冒險的情況;應用最大似然估計法，估計出的最大抖振響應值較試驗值略高，屬于偏保守的設計。兩種參數估計算法得到極值估計精度都在±5%以內，適于工程應用，且整體來說最大似然估計法的精度要略高于最小二乘法。

表2 兩種參數估計方法的結果比較Tab.2 Comparison between results obtained by two parameter estimation methods

3.2 關于測試數據樣本量的討論

由于在實際的動態信號測量過程中，穩定狀態持續時間和數據采集時間總是有限的。尤其對于飛機的飛行測試試驗，飛行參數及姿態持續穩定的時間非常短。本節將從進行長期極值有效估計的角度，討論測試數據樣本量對估計精度的影響，以便確定合理的采樣長度。

以圖2所示24 s秒長度的測試數據為例，分別截取時間長度為 0.5 s，1 s，1.5 s，2 s，2.5 s，5 s，24 s 的數據，按Ⅲ型分布模型應用最大似然估計法進行參數估計，并進行極值預測。同時對不同長度的樣本數據求相應的均方根值，并按照傳統的3σ法則估計設計載荷，以便對比。

計算結果如表3所示，應用2 s長數據，32個統計樣本，進行參數估計，即可較為準確的識別分布模型參數，對應24 s重現期估計得到的極值與實際極值之間的誤差小于5%。并且由識別參數隨樣本數量變化趨勢可見，參數識別結果隨樣本數量的增加趨于穩定。而簡單由3σ法估計的設計載荷明顯低于24 s內的極值載荷。如果采用4σ，則基本逼近24s內的極值載荷。更進一步，由不同時間長度數據得到的均方根值變化可知，對于本文所分析的平穩過程數據，僅0.5 s數據即可準確獲得振動響應的基本統計特征。這說明平穩過程的數據樣本長度對均方根值計算的影響不大。但是如要根據均方根值來估計長期極值，則需要借用合理的判據來確定σ的放大倍數，而本文所提的極值估計法恰好可以用來實現合理倍數的估計。

3.3 長期極值估計

假定圖2所示的數據表示飛機在以下飛行條件下的典型抖振響應數據。3 000 m高度巡航，馬赫數Ma=0.6，機翼迎角 αw=4°，方向舵偏角 15°(尾部結構抖振響應對方向舵偏角比較敏感，所以選用該參數進行狀態劃分)。以該數據段作為一個劃分后的典型狀態代表。

設每個飛行小時內，該狀態的累計發生時間為300 s，飛機的設計壽命為6 000飛行小時。據此可以推斷在飛機的整個壽命周期內該狀態可能發生的總持續時間為 1 800 000 s。取 Δt=0.062 5 s，按照式(2)式(3)設定tN=1 800 000 s，可求得設計超越概率為:

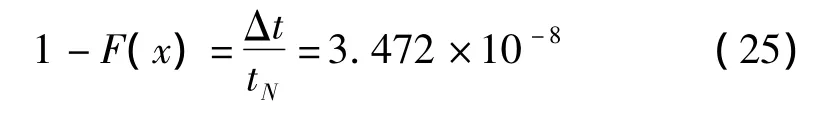
將式(25)代入到式(1)，并且根據事先得到的估計參數，可求得對應的設計極值為1.145。

4 結論

本文利用次序統計和長期極值估計理論，結合某型飛機尾部結構的抖振風洞試驗數據，應用極值Ⅰ型分布和Ⅲ型分布參數進行了抖振響應極值估計研究，相關結論如下:

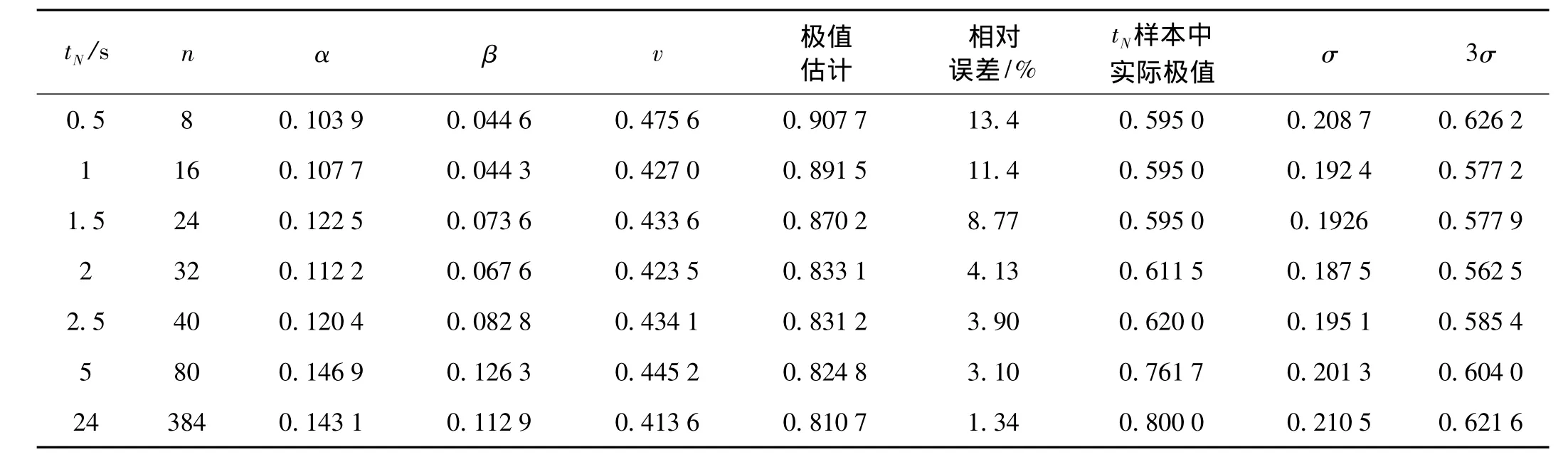
表3 樣本長度對估計精度的影響(Ⅲ型分布，最大似然法估計)Tab.3 Prediction accuracy varies with tN(distribution Ⅲ ，maximum likelihood method)

(1)對于平穩隨機過程，Ⅰ型分布模型的極值估計精度明顯沒有用Ⅲ型分布模型估計的精度高。原因在于Ⅰ型分布為雙參數模型，難以準確描述長尾分布，三參數的Ⅲ型分布模型明顯改善了超越概率曲線的后段描述精度。

(2)在數據樣本足夠的情況下，最小二乘法估計法和最大似然估計法都可以較為準確地實現分布參數估計，極值估計精度在±5%范圍內，適于工程應用。但總體趨勢上最大似然估計法的估計精度略高于最小二乘法。

(3)通過數據對比分析可知，對平穩隨機振動過程，傳統的3σ設計原則不能滿足飛機設計中對確定限制載荷的要求，根據3σ設計原則確定的限制載荷將偏危險。長期極值估計法更加符合飛機限制載荷的確定要求，值得在工程設計中進行推廣應用。

(4)要實現飛機抖振載荷準確有效的極值估計，對采集樣本數量有一定的基本要求。該基本要求可以確定最小響應采集時間，該指標對于振動響應測試方案和數據處理方法的制定有一定的指導性意義。

［1］Lee B H K.Vertical tail buffeting of fighter aircraft［J］.Progress in Aerospace Sciences，2000，36:193 －279.

［2］中國民用航空管理局.中國民用航空規章第25部:運輸類飛機適航標準(CCAR－25－R4)［S］.北京:中國民用航空局，2011.

［3］HoblitF M. GustLoads on Aircraft:Concepts and Applications［M］.USA:AIAA，1988.

［4］Patel S R，Black C L，Anderson W D.F/A－22 Vertical tail buffet strength certification［C］.46th AIAA/ASME/ASCE/AHS/ASC Structures，StructuralDynamics ＆ Materials Conference，Austin，Texas，2005.

［5］Lee B H K.Statistical analysis of wing/fin buffeting response［J］.Progress in Aerospace Sciences，2002，38:305 －345.

［6］段忠東，歐進萍，周道武.極值風速的最優概率模型［J］.土木工程學報，2002，35(5):11 －16.DUAN Zhong-dong，OU Jin-ping，ZHOU Dao-wu.The Optimal Probabilistic Distribution for Extreme Wind Speed［J］.Journal of China Civil Engineering，2002，35(5):11 －16.

［7］趙 偉，楊永增，于衛東，等.長期極值統計理論及其在海洋環境參數統計分析中的應用［J］.海洋科學進展，2003.24(4):471－476.ZHAO Wei，YANG Yong-zeng，YU Wei-dong，et al.Longterm extreme value statistics theory and its application to the marine environmental parameter statistics and analysis［J］.Advances in Marine Science，2003，24(4):471 －476.