土壤溶質遷移的指數函數模型

魏 峰，王全九

（西安理工大學，西安710048）

工業“三廢”的排放，農業生產中化學物質（化肥、農藥等）的大量施用導致了嚴重的環境污染，威脅到了人類的生命健康。許多專家學者越來越注重研究土壤水分及土壤溶質的遷移規律，建立各種數學模型預測和控制土壤溶質的遷移過程，并估計溶質遷移參數［1－7］。人們對土壤溶質的遷移機理多以對流一彌散方程（Convection－Dispersion Equation，CDE）描述。而模型中參數的確定又成為土壤溶質遷移研究的一個重要問題。國內外學者投入大量精力，尋求土壤溶質的遷移模式、遷移參數的確定方法［6－9］。Shao等［6］和Wang等［7］在分別假定溶質濃度分布為二、三次多項式和四、五次多項式的基礎上，提出了確定CDE方程中參數及其近似解的邊界層理論模型，研究結果表明，邊界層理論可應用于土壤溶質遷移的研究。鄭紀勇等［9］從實驗的角度對邊界層方法（三次邊界層解）進行了研究，認為隨時間的增加，邊界層方法計算的結果與精確方法計算的結果之間的誤差會逐漸增大。本文在此基礎上，假定土壤溶質濃度剖面為指數函數，得到描述溶質濃度分布的指數函數模型。分析各參數對邊界層距離的影響以及不同模型預測土壤溶質分布情形。

1 相關理論

穩態水流條件下，均質土壤一維瞬態溶質遷移通常由對流－彌散方程（CDE）來描述：

式中：c——土壤溶質濃度；x——坐標；t——時間；v——平均孔隙水流速；D——彌散系數；R——延遲因子。

初始條件和邊界條件為：

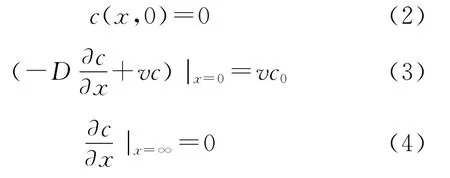
式中：c0——初始溶質濃度。

Shao等假定土壤溶質遷移存在邊界層，且土壤溶質濃度分布可以用二次或三次冪函數表示。同時在邊界層處，土壤溶質濃度應符合下列條件：

由上述條件Shao等獲得了土壤溶質濃度剖面表達式。對于二次冪函數，濃度剖面和邊界層距離為：

為進一步比較描述土壤溶質濃度的邊界層方法，Wang和Horton在假定一定邊界層距離條件的基礎上推求出了四次和五次冪函數的邊界層解。對于四次冪函數，濃度剖面和邊界層距離為：

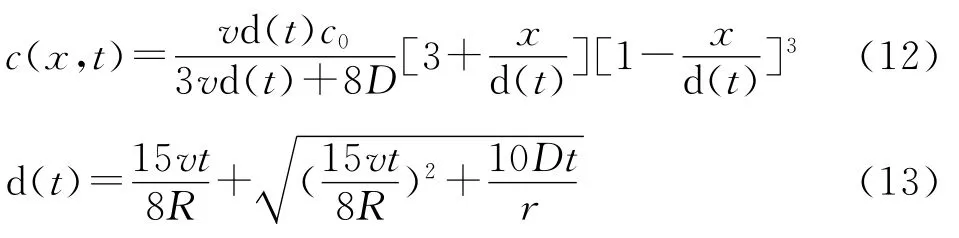
對于五次冪函數，濃度剖面和邊界層距離為

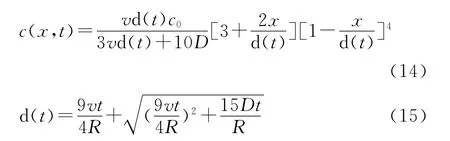
基于Shao等與 Wang和Horton的思想，假定土壤溶質遷移的濃度剖面為指數函數，得到了描述溶質濃度分布的指數函數模型。

假定土壤溶質濃度分布可以用指數函數表示：

在邊界層處，土壤溶質濃度應符合下列條件：

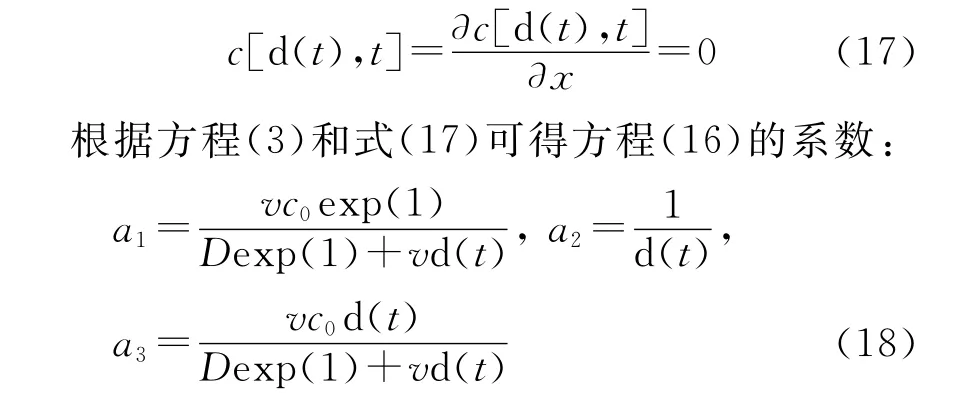
將式（18）代入方程（16）即得n次冪函數的土壤溶質濃度剖面：

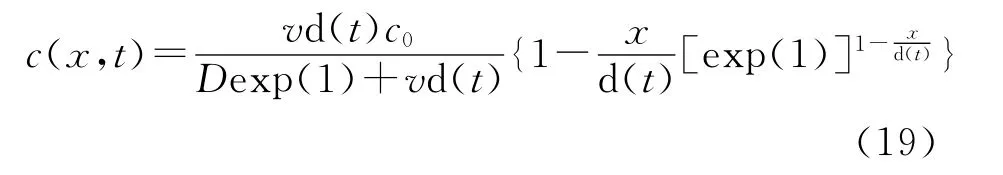
方程（19）當0≤x＜d（t）時成立，當x≥d（t）時設c（x，t）＝0。

結合方程（19）和（7）可得n次冪函數的土壤溶質邊界層距離：

式（19）是對流—彌散方程（1）的一種廣義近似解，相比較邊界層解（19）比精確解（21）表示簡單，應用方便。

2 結果與分析

2.1 各參數對邊界層距離隨時間變化的影響

由式（20）可見邊界層距離是時間的增函數，但邊界層距離隨時間的增加受各參數的影響。

2.1.1 R對邊界層距離隨時間變化的影響 對于給定的水流速度（v）和彌散系數（D），隨著延遲因子的增加，溶質鋒面運動曲線下移，邊界層距離減小（圖1）。說明R的增加降低了溶質遷移的速度。

2.1.2 D對邊界層距離隨時間變化的影響 對于較小的孔隙水流速度（v），當彌散系數（D）較小時邊界層距離隨時間緩慢增加，而當彌散系數（D）較大時邊界層距離隨時間增加比較快。這說明對較小的孔隙水流速度，彌散系數（D）對邊界層距離影響最大（圖2a）。對較大的孔隙水流速度（v），彌散系數（D）對邊界層距離影響不太大（圖2b和2c）。取v＝0.2時D＝0.1、D＝0.01和D＝0.0013條線幾乎重合，這時邊界層距離主要由孔隙水流速度（v）影響著（圖2b—2c）。

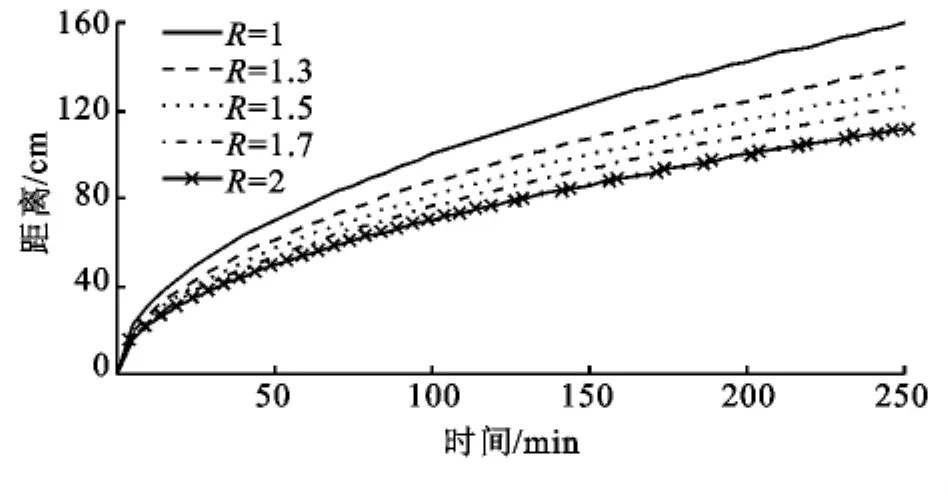
圖1 R對邊界層位置的影響

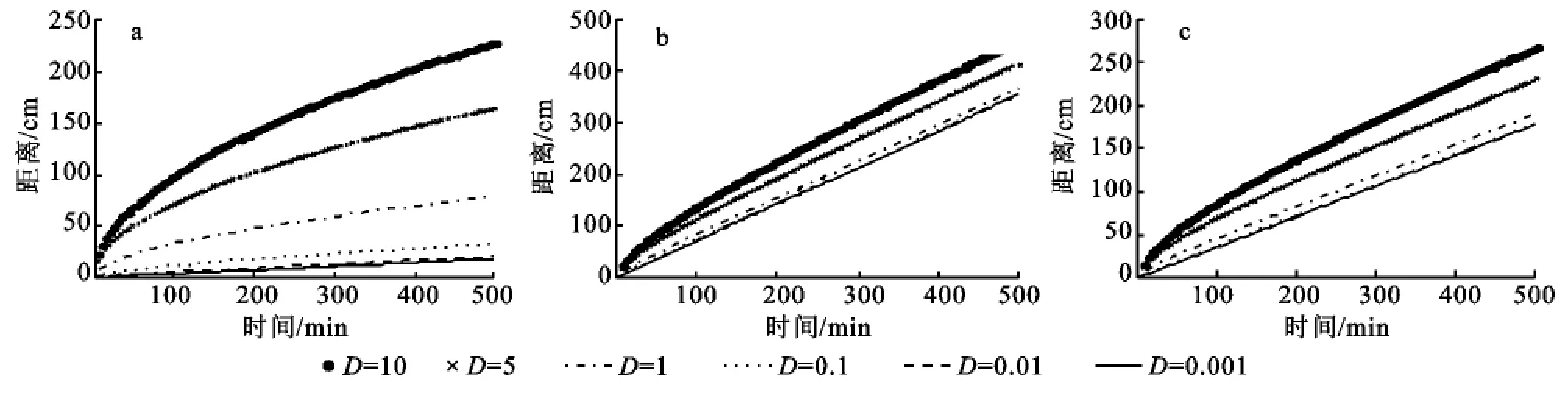
圖2 D對邊界層位置的影響

因為邊界層距離也是關于彌散系數（D）增函數，而且有：

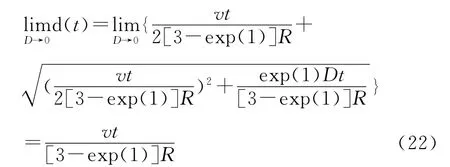
所以對于給定的孔隙水流速度（v），無論是惰性非吸附性溶質（R＝1）還是吸附性溶質（R≠1），隨著彌散系數（D）的減小，溶質鋒面運動曲線逐漸下移，并越來越趨近于直線，d（t）（圖2）。

2.1.3 v對邊界層距離隨時間變化的影響 對較小的彌散系數（D），當孔隙水流速度（v）較小時邊界層距離隨時間緩慢增加，而當孔隙水流速度（v）較大時邊界層距離隨時間增加比較快。這說明對較小彌散系數（D），孔隙水流速度（v）對邊界層距離影響最大，如圖3a。對較大的彌散系數（D），孔隙水流速度（v）對邊界層距離影響不大（如圖3b—3c）。取D＝2時v＝0.01、v＝0.005和v＝0.001三條線幾乎重合，這時邊界層距離主要由彌散系數（D）影響著。

因為邊界層距離也是關于孔隙水流速度（v）增函數，而且有：

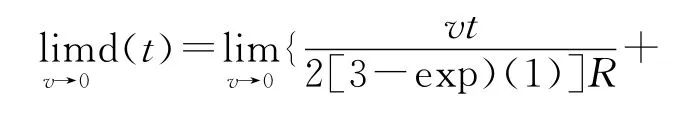
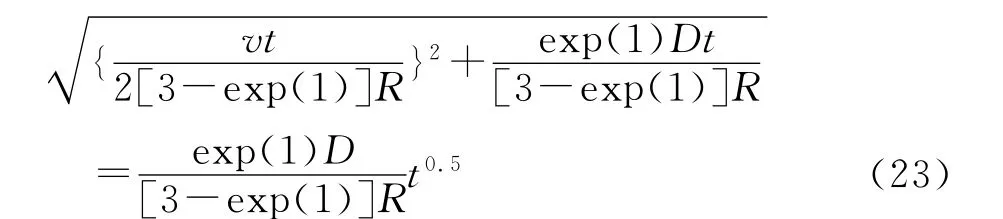
所以對給定的彌散系數（D），無論是惰性非吸附性溶質（R＝1）還是吸附性溶質（R≠1），隨孔隙水流速度（v）的減小，溶質鋒面運動曲線逐漸下移，并越來越趨近于拋物線（圖3）。

2.1.4 彌散度（D／v）對邊界層距離隨時間變化的影響 實驗室土壤柱彌散度（a＝D／v）為0.5～2cm；田間土壤彌散度為5～20cm；而對于區域地下水彌散度可能達到很大的值。劉春平和邵明安［11］的研究表明，對于一個給定的孔隙水流速度v＝0.003cm／min，鋒面深度隨彌散度的增加而增加，彌散度在10～40cm比在0.5～10cm范圍溶質鋒面深度增加要快；對給定的彌散系數D＝0.03cm2／min，當彌散度從0.5cm到10cm增加時，鋒面深度有一個小的增加，當彌散度從10cm到40cm，鋒面深度增加更快。這意味著當v達到一個較大值時，對鋒面運動有一個較大的影響。實際上，對于一個給定的孔隙水流速度，鋒面深度隨彌散度的增加而增加（圖4）；對于一個給定的彌散系數，鋒面深度隨彌散度的增加而減小（圖4）。由圖4可知，無論是惰性非吸附性溶質（R＝1）還是吸附性溶質（R≠1），彌散度對邊界層距離的影響沒有一定規律。

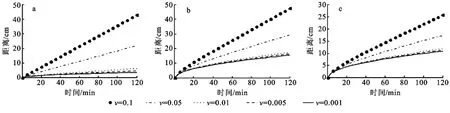
圖3 v對邊界層位置的影響

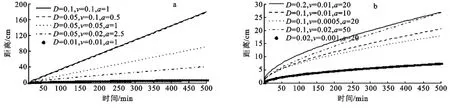
圖4 a對邊界層位置的影響（a）R＝1；（b）R＝2

2.2 邊界層解與精確解比較

邊界層解只是一個近似解，下面我們將其與精確解作一比較。Shao等比較了二、三次邊界層解與精確解，認為邊界層解和精確解相近。Wang等分析了三、四、五次邊界層解與精確解，認為它們大多情況下也與精確解相近，有些情況下五次邊界層解比其他較好。他們在短距離處并且只在某一時刻作了比較分析。在較大尺度且在多時刻對邊界層解與精確解作分析比較發現，對較小的孔隙水流速度，時間較短時三、五次和指數型邊界層解與精確解都很相近，指數模型要好于其它，但隨著時間的增加誤差越來越大，誤差的變化和延遲因子及彌散系數的變化又有很大關系（圖5a—c）。從圖5d—f可見，對較大孔隙水流速度，邊界層解與精確解誤差與彌散系數有很大關系。彌散系數越小邊界層解與精確解誤差越大，這時二次邊界層解要好于其它（圖5d—f）；而彌散系數越大邊界層解與精確解誤差越大小，特別是在小時間段，三、五次和指數模型邊界層解要好于其它（圖5e）。相同條件下，用邊界層方法對吸附性溶質的濃度模擬要比非吸附型溶質要好（圖5c—f）。

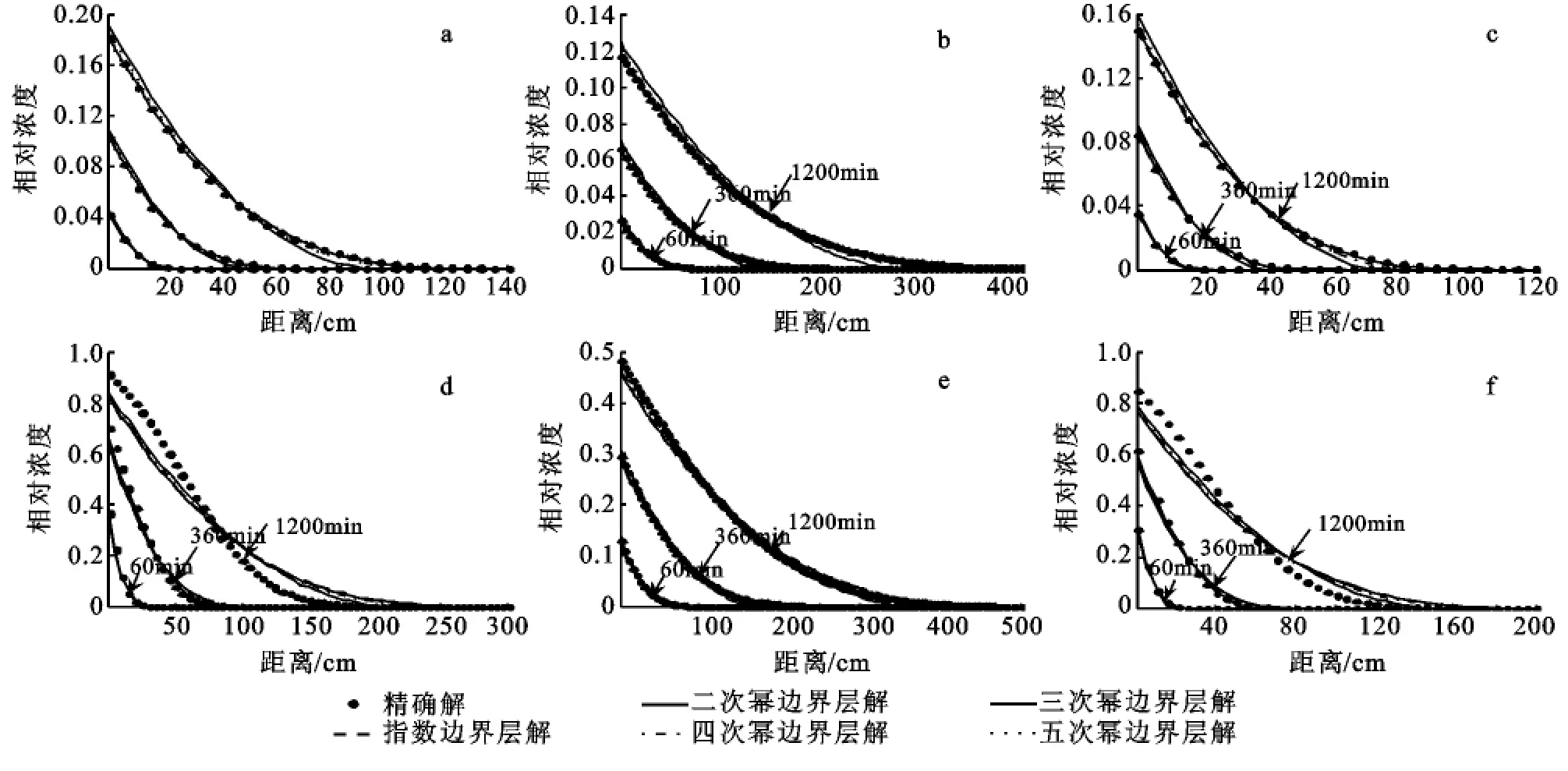
圖5 邊界層解與精確解比較

對邊界層與精確解的誤差作分析，對較小孔隙水流速度，在長距離處，五次邊界層與精確解的誤差比其他小；而在短距離處，指數型邊界層幾乎比其他都要小。對較大孔隙水流速度，邊界層解與精確解受各因素影響較大，它們之間的誤差變化較大，沒有規律。

2.3 參數的確定

邊界層距離是時間、遷移參數的簡單初等函數，因此容易通過邊界層運動隨時間變化估計溶質遷移參數。溶質鋒面是一個遷移物質在遷移過程中從無到有的界面，而時域反射儀（TDR）則是一種新的用于溶質遷移研究的設備。溶質鋒面未達到一定深度探測點前，TDR探針所探測到的濃度值恒定不變，當濃度值發生變化時，就認為此時為溶質鋒面遷移到此探測點的時間。根據不同探測點深度d（t）以及相應的時間t，結合方程（20），經過數據處理，得到用邊界層確定的運移參數彌散系數和延遲因子。綜上，邊界層解只是一個近似解，雖然表述、計算簡單，但也受各因素影響。特別是當孔隙水流速度越大、彌散系數越小邊界層解與精確解誤差越大。因此運用邊界層方法推求相關參數時，應取較小的孔隙水流速度、短歷時。

3 結論

邊界層解是CDE方程的一個簡單近似解，通過邊界層距離隨時間變化可以估計溶質遷移參數。本文將描述土壤溶質遷移的邊界層理論推廣到一般，得到了描述溶質濃度分布的指數函數模型。從邊界層方法在各種參數組合不同時段內的土壤溶質分布模擬來看，在較短歷時具有較高的精度，對孔隙水流速度大、彌散系數小的情況模擬的誤差大。研究表明指數函數模型應選取較小的孔隙水流速度、短歷時推求溶質遷移參數。

［1］ van Genuchten M Th，Wagenet R J.Two－site／two－region models for pesticide transport and degradation：theoretical development and analytical solution［J］.Soil Sci.Soc.Am.J.，1989，53（5）：1303－1310.

［2］ Wallach R，Grigorin G，Rivlin J.A comprehensive mathematical model for transport of soil－dissolved chemicals by overland flow［J］.Journal of Hydrology，2001，247（1／2）：85－99.

［3］ Wang Q J，Horton R，Lee J.A simple model relating soil water characteristic curve and solution breakthrough curve［J］.Soil Science，2002，167（7）：436－443.

［4］ Gao Bin，Walter M T，Steenhuis T S，et al.Rainfall induced chemical transport from soil to runoff：theory and experiments［J］.Journal of Hydrology，2004，295（1／4）：291－304.

［5］ Pathak D R，Hiratsuka A.An integrated GIS based fuzzy pattern recognition model to compute groundwater vulnerability index for decision making［J］.Journal of Hydro－environment Research，2011，5（2）：93－99.

［6］Shao M，Horton R，Miller R K.An approximate solution to the convection－dispersion equation of solute transport in soil［J］.Soil Science，1998，163（5）：339－345.

［7］ Wang Q J，Horton R.Boundary layer theory description of solute transport in soil［J］.Soil Science，2007，172（11）：835－841.

［8］ Kool J B，Parker J C，van Genuchten M.Parameter estimation for unsaturated flow and transport model：a review［J］.Journal of Hydrology，1987，91（3／4）：255－293.

［9］ 鄭紀勇，邵明安.應用邊界層方法確定溶質遷移參數的實驗研究［J］.水利學報，2002（1）：92－96.

［10］ Lindstrom F T，Haque R，Freed V H，et al.Theory on the movement of some herbicides in soil：linear diffusion and convection of chemicals in soils［J］.Environ.Sci.Technol.，1967，1（7）：561－565.

［11］ 劉春平，邵明安.土壤溶質鋒運移的解析解［J］.水土保持學報，2001，15（4）：82－86.