深埋公路隧道在雙向地震動作用下的最大動力反應分析①

孫 文，梁慶國，安亞芳，歐爾峰

（1．甘肅省道路橋梁與地下工程重點實驗室 甘肅 蘭州 730070；2．蘭州交通大學 土木工程學院 甘肅 蘭州 730070）

0 引言

隧道結構的震動特性與地面結構有很大不同。早期認為隧道因其圍巖具有足夠的剛度從而保證隧道在地震中不會受到太大的影響，隧道結構的抗震能力與地面結構相比具有天然的優勢，故對地面結構的抗震措施研究較多［1］。然而，近年來的幾次地震中隧道結構出現的嚴重破壞對以上觀點提出了新的挑戰，如1995年阪神地震造成災區內10%的山嶺隧道受到嚴重破壞；1999年臺灣集集地震后，臺灣中部距發震斷層25km范圍內的44座受損隧道中嚴重受損者達25%，中等受損者25%；2008年汶川地震中附近地區的大部分隧道也出現了嚴重的損壞［2－3］。

目前隧道與地下結構的抗震分析方法主要有原型觀測、模型試驗和數值模擬等幾類。有很多種數值模擬的方法和相應的軟件，如有限元方法的ANSYS［4］、有 限 差 分 法 的 FLAC3D［5］和 離 散 元 的UDEC等［6］，其中尤以有限元方法的使用最為廣泛，已成功應用于多個隧道與地下結構的抗震分析。

通常在隧道的有限元數值分析中多僅考慮單一方向的地震波施加［7］，然而很多情況下地震動方向與隧道是斜交的，此時隧道可能由此而發生多個方向的震動。所以，本文采用MIDAS／GTS軟件分別對模型施加單向和雙向地震作用，通過對比在自重作用、單向和雙向地震作用下隧道襯砌結構的動力響應特點，得出在更接近真實地震情況下的隧道抗震設計的建議，為工程實踐應用提供一定的參考。

1 工程概況

武罐高速是蘭州至海口國家高速公路的重要組成部分，位于甘肅省與四川省交界的山嶺地區。本文選取該段線路的特長隧道之一——小石村隧道進行數值分析。小石村隧道隧址區位于西秦嶺山地中低山地貌的峽谷地帶。隧道左線全長3 424m，隧道最大埋深約224．8m；右線全長3 367m，隧道最大埋深約220m。研究段為Ⅴ級圍巖，按新奧法施工；采用復合式襯砌，二次模筑襯砌拱部、邊墻采用C25防水混凝土，仰拱采用C25普通混凝土。

2 數值模型

2．1 計算軟件

采用 MIDAS／GTS（2．60版本）模塊進行隧道地震動力響應分析，故以下有關理論方法及參數選取等參照MIDAS／GTS的軟件功能來論述。

2．2 單元類型及有限元模型

模型采取的計算范圍：X方向120m、Y方向15 m、Z方向264m。隧道跨度10．25m，凈空高度5 m，初襯厚度0．35m，二次襯砌厚度0．5m，洞間距39m，如圖1所示。其中水平橫向地震動沿X軸方向（垂直于隧道軸向）輸入，水平縱向地震動沿Y軸方向（隧道軸向）輸入，垂直向地震動沿Z軸方向（重力方向）輸入。為了提取軸力、彎矩、剪力數據，模型中二次襯砌采用板單元模擬。

圖1 計算模型Fig．1 Computational model．

根據研究需要，對應力應變復雜且重要的襯砌部位及其周圍圍巖依據襯砌形狀特點采用均勻密集的網格劃分，由襯砌向水平兩側和向深度方向隨距離的增加，均勻劃分的網格可逐漸放大。網格劃分采用8節點單元，節點總數39 003個，單元總數207 943個。

2．3 本構模型與計算參數

對圍巖和初期支護等實體單元，采用Mohr－Coulomb屈服準則及彈塑性增量型本構關系。根據設計資料和《公路隧道設計規范》（JTG D70－2004）［8］，確定襯砌和Ⅴ級圍巖的靜力學參數，其中圍巖參數取規范給出范圍的中間值。在進行動力計算分析時，由于應變率效應，動力學參數將在靜力學參數的基礎上有所增大，故對動力學計算參數依照王思敬等擬合出的動彈性模量（Ed）和靜彈性模量（Es）的經驗公式Es＝0．026E1．7d確定［9］。動泊松比則近似按0．8倍的靜泊松比確定［10］。其余參數則保持不變。計算出的經過修正以后的圍巖和襯砌的力學參數如表1。

2．4 模型地震波選取及振型組合方式

在地震反應分析中，常使用離散的載荷列表，因此在施加之前有必要進行濾波和基線校正，即通過在原始加速度時程上增加一個低頻率的波形（多項式或周期函數），使最終的速度和位移均為0。本研究中的地震動加速度時程由中國地震局蘭州地震研究所提供，其超越概率為50年10%。經基線校正的小石村隧道的地震加速度時程曲線如圖2所示，其中加速度峰值為－251．94cm／s2，出現在5．560 s，震動主要集中在5～15s之間。

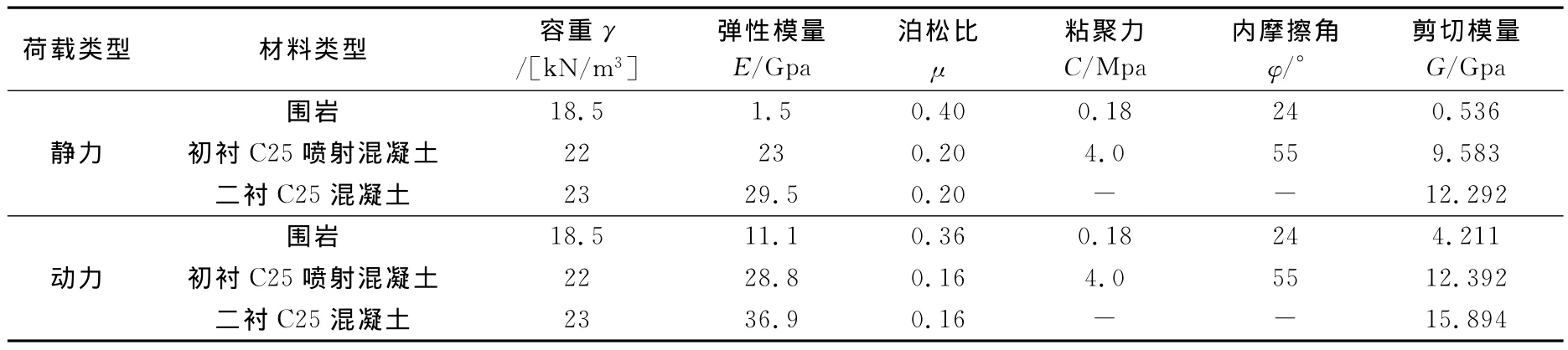
表1 靜力與經修正后的動力學計算物理力學參數

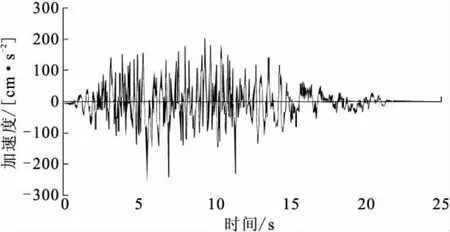
圖2 50年10%超越概率的加速度時程曲線Fig．2 Acceleration time curve with 10%exceedance probability in 50years．

垂直向地震動取相應水平向地震動峰值的2／3［11］，其余水平橫向 （X向）輸入 和縱向 輸入 （Y向）時，直接取經過基線校正的地震動加速度時程曲線。雙向地震波組合方式：XZ、XY、YZ。

3 計算方法

3．1 振型分析

首先對模型進行振型分析，求取有限元體系的特征周期，以計算其阻尼參數。在 MIDAS／GTS中，進行特征值分析時采用彈性邊界條件，一般用曲面彈簧來定義，彈簧系數用地基反力系數計算，方法如下：

垂直地基反力系數

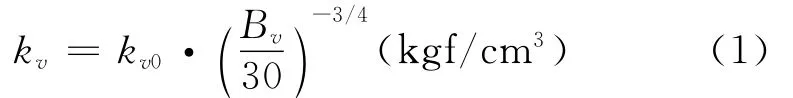
水平地基反力系數

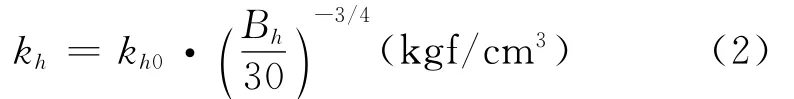
根據上述方法求得的最大周期分別為1．140s和0．516s，依次作為求取瑞利阻尼參數的輸入值，繼而進行數值模型的時程分析［12］。

3．2 邊界條件

動力分析時，適應于一般靜力學分析的邊界條件會由于波的反射作用而產生較大誤差，故采用1972年Lysmer和Wass提出的粘性邊界（Viscous Boundary）。在MIDAS／GTS有限元分析軟件中通過曲面阻尼彈簧來實現。為了定義粘性邊界需要計算相應的巖土體在X，Y，Z方向上的阻尼，單位面積上的阻尼按式（3）和（4）計算：法向阻尼常數

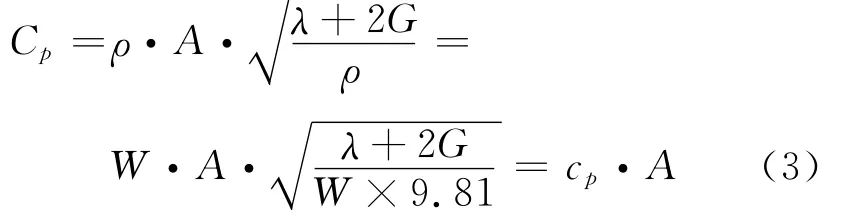
切向阻尼常數

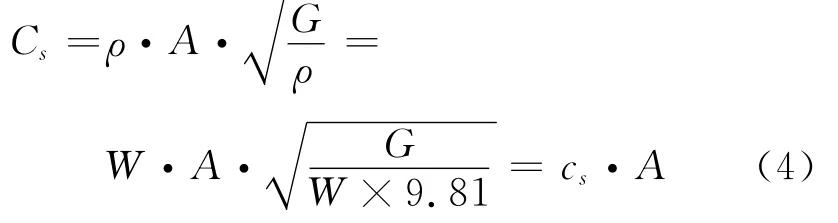
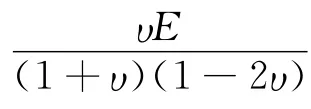
4 計算結果和分析

4．1 監測點分布

動力有限元數值計算結果的監測點分布如圖3所示。其中，位移、速度、加速度監測點22個，軸力、彎矩、剪力監測點16個。

由于數值模型的結果在縱向（Y方向）變化不大，且根據文獻［13］的研究，在地震中隧道的二次襯砌往往會整體垮塌，為抗震的主體部分［13］，在地震動過程中的最大反應一般是動力分析和抗震設計的重點，故以下只給出部分關于隧道二次襯砌最外側截面最大動力反應的結果。

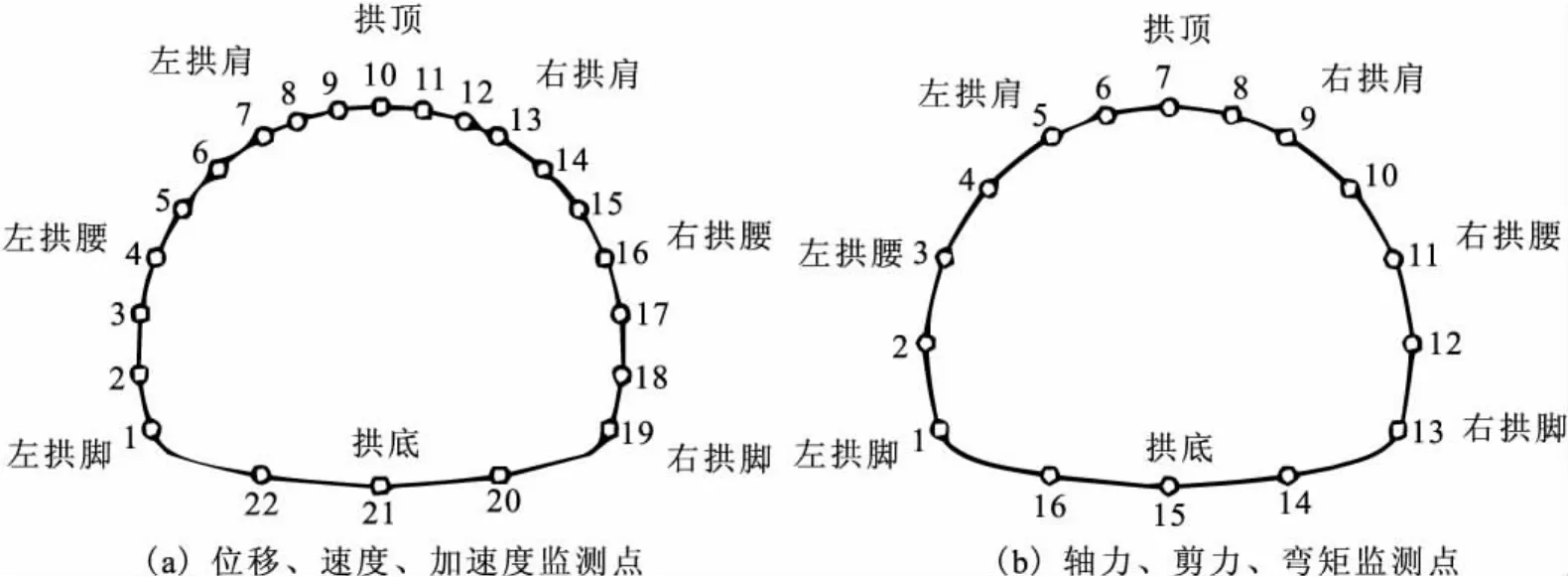
圖3 二襯監測點分布Fig．3 Distribution of observation points on the lining．

4．2 雙向地震動作用與單向地震動作用

首先對單向地震動作用下的隧道模型進行了計算，對各監測點峰值進行了分析，得出了隧道在受單向地震動作用時易發生破壞的位置，然后輸入雙向地震動，對比單向地震動作用與雙向地震動作用時隧道的動力響應。在單向地震動的工況分為三種，即地震動分別從X向、Y向和Z向輸入，所用地震動波形與雙向地震動的波形相同。通過計算，得知模型在地震動輸入為Y向時各項數值最大，原因是水平向地震動保留了地震的大部分能量。一般的隧道動力分析都采取水平向地震動進行計算，所以在后面單、雙向地震動結果對比中以Y向地震動的數據為基準。單向地震動作用與雙向地震動作用類似，易破壞位置都集中在拱頂，拱腳部位。相對于單向地震動作用，雙向地震動作用的峰值均大于單向。單向和雙向地震動各有三種方向組合，選取單、雙向地震動作用中產生最大位移的組合（Y、YZ），分別繪制單、雙向地震動作用下拱頂處最大位移時程曲線（圖4）。

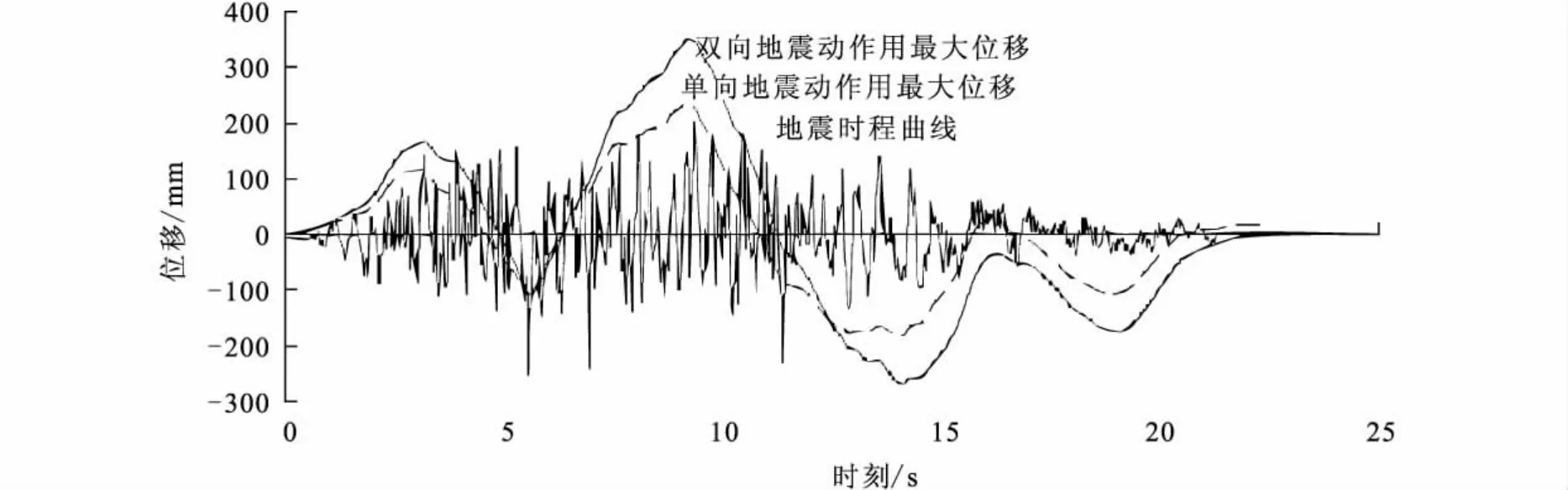
圖4 單向作用與雙向作用最大位移對比Fig．4 Comparison of maximum displacements under unidirectional and bidirectional motions．

兩種情況的位移時程走勢較為相似，但雙向地震動作用的位移幅度明顯大于單向地震動。兩種工況拱頂最大位移出現在9．200s附近，而地震加速度時程曲線的最大值出現在5．560s，體現出了位移在地震作用下的滯后性。

4．3 雙向地震動作用位移、速度、加速度

當地震動輸入方向為YZ組合時，二次襯砌產生的位移值最大，位移云圖如圖5所示。

從云圖中看出結構各部位位移差值不大。通過數據的對比發現，產生位移最大值的組合為YZ組合，其值為350．5mm，位于右拱肩；產生速度最大值的組合為XZ組合與YZ組合，其值為25．7cm／s，位于左拱腰；產生加速度最大值的組合為YZ組合，其值為2．5m／s2，位于拱頂。此外，已知在位移值中各組合中最大值出現在YZ組合，計算得XZ、XY組合最大值分別是YZ組合的98%和67%；速度最大值中各組合中最大值出現在為XZ、YZ組合，計算得XY組合最大值是XZ、YZ組合的87%；加速度最大值中各組合中最大值出現在XZ、YZ組合，計算得XY組合最大值是XZ、YZ組合的92%。由最大值的出現位置可發現，拱頂，拱腰處是地震動作用下的易破壞位置，在隧道施工中應注意這些位置的抗震強化。

在單向地震動作用中，計算得水平向地震動（Y向）時位移、速度、加速度峰值分別為3．34mm，2．99cm／s，1．18m／s2。雙向地震動作用位移、速度、加速度最大值與單向地震動作用對比如表2所示。

圖5 YZ組合地震波作用二襯Z向位移最大值云圖Fig．5 Maximum displacement nephogram in Zdirection of second liner under YZcombine motions．

由表2可知，雙向地震動組合為XY時，隧道二次襯砌的各項峰值與單向地震動的峰值大小十分接近，可見Z向地震動是使隧道結構產生破壞的主要因素。

4．4 雙向地震動作用軸力、彎矩、剪力結果

對比分析表明，軸力出現最大值的組合為YZ組合，其值為1 220kN，XY組合略小；彎矩出現最大值的組合為YZ組合，其值為71．77kN·m，XY組合略小；剪力出現最大值的組合為XY組合，其值為60．26kN，YZ組合略小。隧道二襯右拱腳處彎矩（YZ）、左拱腳剪力（XY）時程曲線如圖6。

圖6（a）中，彎矩最大值為71．77kN·m，出現在6．000s，地震加速的最大值出現在5．560s，可見結構彎矩對地震作用的響應較為及時。圖6（b）中，剪力的最大值為60．26kN，出現在11．040s，但在5．560s附近剪力值明顯較大，和地震動的同步作用較為明顯。

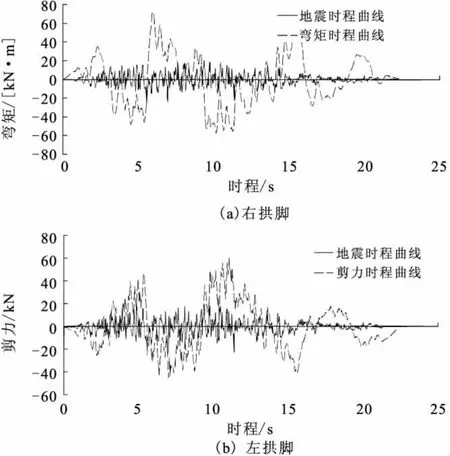
圖6 二襯左右拱腳彎矩時程曲線（YZ）Fig．6 Moment time curves at the right arch and left arch springing of lining（YZ）．

此外在軸力值中，各組合中最大值出現在YZ組合，計算得XZ、XY組合最大值分別是YZ組合的21%、89%；彎矩值中各組合中最大值出現在YZ組合，計算得XZ、XY組合最大值分別是YZ組合的25%、96%；剪力值中各組合中最大值出現在XY組合，計算得XZ、YZ組合最大值分別是XY組合的42%、91%。

由峰值出現的位置發現，拱腳，及拱頂處是地震動中的易破壞位置。特別軸力和剪力最大值多出現在拱腳處，在拱腳處應注意軸向受拉破壞和剪切破壞；剪力峰值還在拱頂出現，因此拱頂的剪切破壞也不容忽視。

單向地震動作用中，水平向（Y向）地震動作用下軸力、彎矩、剪力的最大值分別為1 110kN，66．68kN·m，51．41kN。雙向地震動作用軸力、彎矩、剪力最大值與單向地震動作用對比如表3所示。

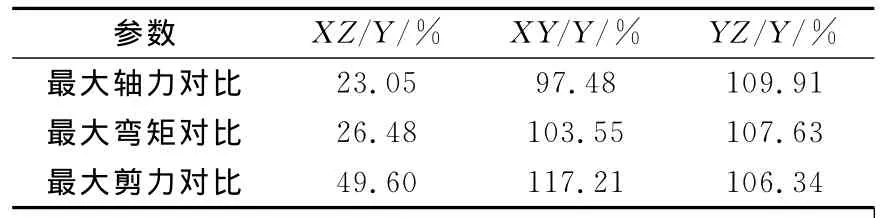
表3 雙向地震動與單向地震動最大軸力、彎矩、剪力對比

由表3可知，雙向地震動組合為XZ時，其產生的峰值偏小，可見隧道縱向（Y向）的地震力對隧道結構軸力、彎矩、剪力的影響較小。

不論是位移、速度、加速度，還是軸力、彎矩、剪力的峰值多發生在拱腳，拱頂部位，與已有的研究結果類似［14］。

4．5 自重作用與地震作用對比

一般認為，地震對深埋隧道的影響較小，因此計算了隧道在自重作用下的響應后，將自重作用，單向地震作用，雙向地震作用下的隧道結構的位移和抗壓安全系數進行了對比，安全系數根據《公路隧道設計規范》（JTG D70－2004）［8］進行計算。

以拱頂為例，自重作用、單向地震作用、雙向地震作用豎向（Z向）最大位移分別為4．6cm、22．9 cm、35．0cm，單向、雙向地震作用分別是自重作用位移的5倍和7．6倍，明顯大于自重作用的位移值。

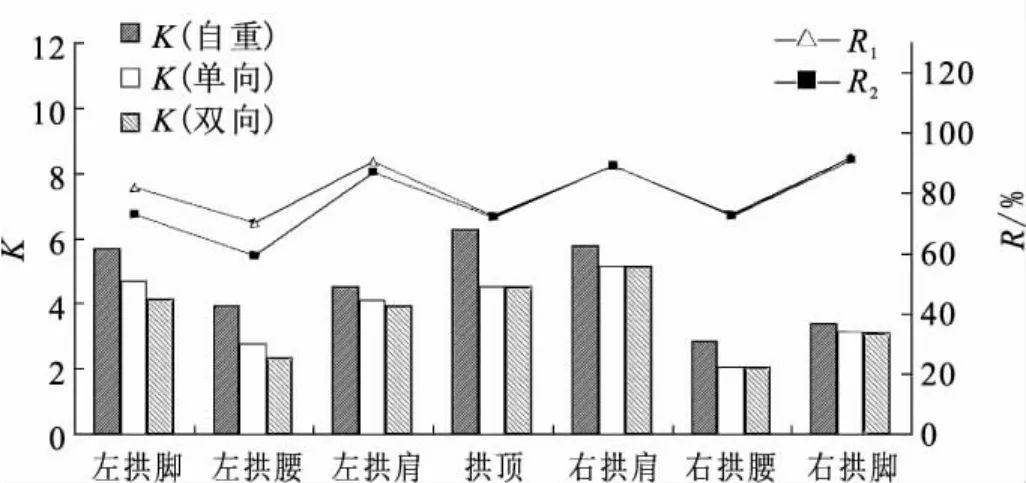
圖7 抗壓安全系數對比Fig．7 Comparison of the compression safety factors．

同時對各工況，使用軸力、彎矩數據對隧道二襯各監測點的抗壓安全系數K進行了計算，如圖7所示。柱狀圖表示安全系數，R1＝K（單向）／K（自重）；R2＝K（雙向）／K（自重），從位移和安全系數K兩個方面的對比結果，都說明地震作用對深埋隧道的影響是不可忽略的，應該注意地震作用對深埋隧道的影響，特別是考慮雙向地震動的效應。

5 討論與結論

（1）軸力峰值較一般論文偏小［15］，分析原因系一般研究普遍采取的是50年超越概率2%的地震波，其強度大于本文中采取的50年超越概率10%的地震波。另外本文采用的動彈性模量和動泊松比比靜力參數有所提高，相當于使圍巖性質變好，級別提高，故結構的動力響應有所減小。

（2）峰值多出現在拱腳和拱頂處，可見隧道結構的拱腳和拱頂處在地震中受到的影響相對于其他部位更大，說明隧道襯砌的連接部位特別是拱腳是隧道抗震的薄弱環節。在設計時可對以上部位做加固處理，如配置一定數量的構造鋼筋，增加柔度等。

（3）各雙向地震動作用下，YZ方向時隧道結構受力最大，可見隧道在受到縱向與豎向組合的地震力作用時，即可認為地震動方向與隧道走向平行或者接近時會對襯砌產生較大影響。Z向（豎向）地震動作用對隧道結構的影響較大。

（4）在隧道的設計中，為了更加接近實際，保證隧道的安全性能，應在單項地震動的基礎上，考慮雙向地震動作用的效應適當加強隧道的強度設計。

（5）在地震作用下，特別是強震作用，深埋隧道的抗震問題是不可忽略的。

［1］ 劉瑋，吳志堅，馬宏旺，等．汶川8．0級地震甘肅隴南地區建筑震害調查［J］．西北地震學報，2010，32（2）：180－185．

［2］ 安永林，彭立敏，黃娟．地震時隧道襯砌受力敏感性的簡化理論分析［J］．西北地震學報，2008，30（3）：261－265．

［3］ 陳正勛，王泰典，黃燦輝．山嶺隧道受震損害類型與原因之案例研究［J］．巖石力學與工程學報，2011，30（1）：45－57．

［4］ 程選生，田瑞瑞，王俊嶺，等．大跨度無襯砌蛋形黃土隧道圍巖結構的靜力和地震動穩定性分析［J］．土木工程學報，2010，43（增刊）：582－587．

［5］ 鐘志輝，劉祚秋，楊光華，等．基于 Midas／GTS的FLAC3D邊坡建模技術及工程應用［J］．西北地震學報，2011，33（增刊）：261－265．

［6］ 張國華．大斷面隧道爆破開挖圍巖損傷范圍試驗研究及數值計算［J］．巖石力學與工程學報，2009，28（8）：1610－1619．

［7］ 何偉，陳建云，溫瑞志．豎向地震動對軟土地鐵隧道地震響應影響分析［J］．四川大學學報（工程科學版），2010，42（5）：271－276．

［8］ 中華人民共和國行業標準．公路隧道設計規范（JTG D70－2004）［S］．北京：人民交通出版社，2004．

［9］ 王思敬，吳志勇，董萬里，等．水電工程巖體的彈性波測試［C］∥中國科學院地質研究所．巖體工程地質力學問題（三）［G］．北京：科學出版社，1980：229－253．

［10］ 戴俊．巖石動力學特性與爆破理論［M］．北京：冶金工業出版社，2002：147－149．

［11］ 胡聿賢．地震工程學［M］．北京：地震出版社，1988：155．

［12］ 潘昌實．隧道力學數值方法［M］．北京：中國鐵道出版社，1995：260－269．

［13］ 高波，王崢崢，袁松，等．汶川地震公路隧道震害啟示［J］．西南交通大學學報，2009，44（3）：336－341．

［14］ 高峰，任俠．黃土窖洞地震反應分析［J］．蘭州鐵道學院學報，2001，20（3）：12－18．

［15］ 皇民，高波，魏來．高烈度區隧道洞口地段響應研究［J］．地震研究，2008，31（2）：180－185．