不定式的極限問題

王曉英，張洪光

（赤峰學院 數學與統計學院，內蒙古 赤峰 024000）

不定式的極限問題

王曉英，張洪光

（赤峰學院 數學與統計學院，內蒙古 赤峰 024000）

不定式的極限是極限計算問題的難點，結構復雜、形式多樣，沒有統一固定的計算方法，可以用初等變換消去零因子、洛必達法則、無窮小代換等，有時候一道題目需要結合使用多種方法，才能化繁為簡，快捷有效的得出結果.本文根據題目的具體形式，重點介紹洛必達法則和無窮小代換的適用情行、注意問題和使用技巧，使學生對計算不定式的極限問題有更深入的理解.

極限；不定式；洛必達法則；等價無窮小

1 關于洛必達法則

定義1當x→a（或x→∞）時，f(x)→0且g(x)→0的極限可能存在，也可能不存在，通常把這種極限叫型不定式.

在所有的高等數學和數學分析教材里，一般都給出四種不同形式的洛必達法則，并用中值定理加以證明，如復旦大學《數學分析》（第三版）237頁，同濟大學（第五版）133頁，本文概述如下；

（2）f與g在x0的某空心鄰域U0(x0)內可導，且g'(x)≠0；

注2定理中的“x→x0”換成“x→±x0、x→±∞、x→∞”只要修改相應的條件（2），也得到同樣的結論.

注4只要f'，g'，f"，g"，f蓯，g蓯…滿足定理條件，洛必達法則可以重復使用.在多次應用洛必達法則時，使用前要檢查是否仍滿足洛必達法則條件，否則會出現錯誤，例如，但若兩次用洛必達法則就得錯誤結果.原因是當x→∞時，c o s x不存在極限，此時不滿足洛必達法則的條件（2）.利用洛必達法則求極限的時候應該注意

注5 洛必達法則是處理未定式極限的重要手段，且非常有效.但它只能直接應用于型和型的未定式.而對于∞-∞,0·∞,∞0,1∞,00等形式，需化為型和型求解.一般的∞-∞可以通分化為標準型;而∞0,1∞,00一般先取對數化為0·∞型進而化為標準型.

解（1）當x→π時，f(x)=1+c o s x和g(x)=t g2x都趨于零，由洛必達法則得

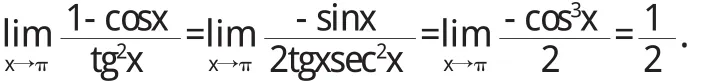
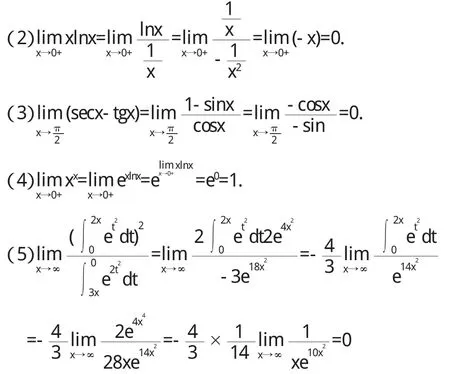
=3，試求f'(0).

解 因為

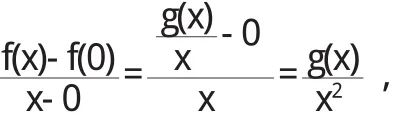
所以由洛必達法則，得

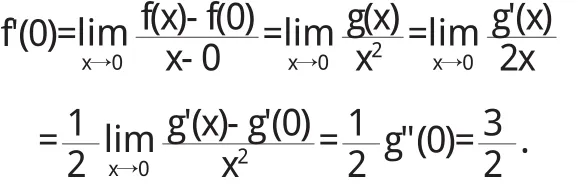
連續兩次用洛必達法則的做法是錯誤的：

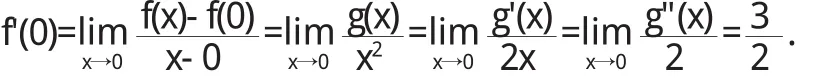
原因在于題設條件只有g在x=0存在二階導數，不知g在x=0的某鄰域內是否也存在二階導數，更不知二階導數在x=0是否連續.

注6 用洛必達法則求數列的極限 用洛必達法則求函數的極限，要求函數在點的鄰域內可導，數列的極限問題，由于不滿足洛必達法則條件，不能直接用洛必達法則計算，有時可以轉換為函數極限問題，進而求出數列的極限.

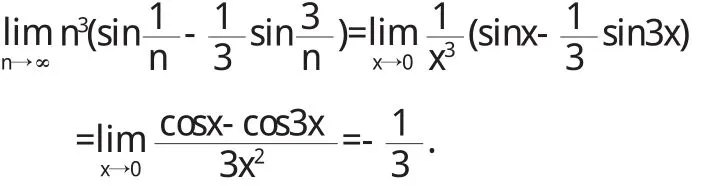
2 關于無窮小等價代換

無窮小具有很好的性質，在求極限的運算過程中，掌握并充分利用好它的性質，往往會使一些復雜的問題簡單化，可起到事半功倍的效果.但代換不當時會產生錯誤.利用無窮小量的代換性質求函數的極限，即將分式函數中的分子、分母，用與其等價的無窮小量來代換.

定義2 在某一變化過程中，以零為極限的量稱無窮小

定義2'如果數列{an}當n→∞時的極限是零，則稱數列{an}為當n→∞時的無窮小.

定義2"如果函數f(x)當x→x0(或x→∞)時的極限是零，則稱函數f(x))為當x→x0(或x→∞)時的無窮小.

定理2 設α,α',β,β',γ等均為同一自變量變化過程中的無窮小，則

（2）若α~β，β~γ，則α~γ,（3）若α~α',β~β'，且l i m=c(c≠-1)，則α+β~α'+β'

定理3 設在自變量的某一變化過程中，α(x)、β(x)、α (x)、β'(x)都是無窮小量.

（1）若α~α'，g(x)為同一過程中的另一函數，且l i m α'g(x) =A，則l i m αg(x)=A

（2）若α~α',β~β'，f(x)為同一過程中的另一函數，且l i m存在，則也存在，且

定理4 設在自變量的某一變化過程中，α(x)、β(x)、α (x)、β'(x)都是無窮小量.

（1）若α~α',β~β'，則對于未定式1∞型有：

證明 （1）在自變量的某一變化過程中

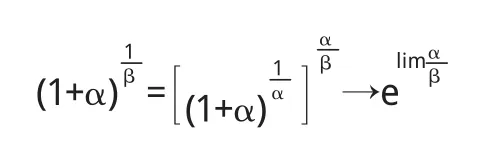
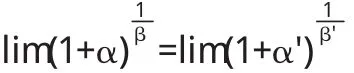
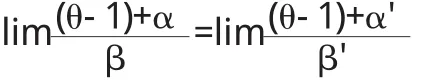
常用的等價無窮小（x→0,a>0且a≠1,α為常數）.

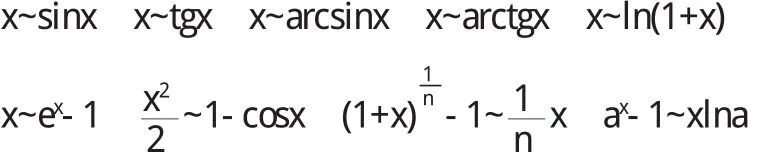
解 因為x→0時當a r c s i n 5 x~5 x,a r c t a n 2 x~2 x,s i n 3 x~3 x，而且所以原式

解 因為當x→0時a r c s i n 3 x~3 x,c o s 2 x→1，而且,所以

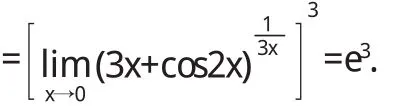
以上例子說明等價無窮小量的代換方法對求函數的極限起到了簡化運算過程的作用，將一些不易求解的極限問題化繁為簡，化難為易，從而得到解決.因此，掌握以上方法，可以使得函數極限的計算更加容易.

3 有效結合多種方法，選擇最優解決途徑

洛必達法則和等價無窮小代換都是解決不定式極限的常用的有效方法，但都有一定的局限性.利用無窮小量的代換性質求函數的極限，能使問題簡化，但是涉及代數和或部分代換時容易出現錯誤，使用時需要謹慎.洛畢達法則也不是萬能的，更不一定是最佳的，有時盡管滿足條件，但把式子越變越復雜，難于求出最后的結果.如計算應用洛必達法則有

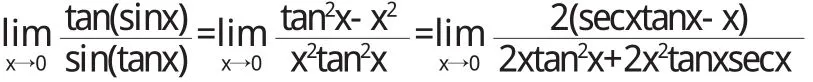
繼續下去表達式會更加復雜.很多時候需要幾種方法結合起來運用，包括初等變形、洛必達法則、等價無窮小代換、級數展開等.

解因為當x→0時s i n x~x,t a n x~x,ex-1~x

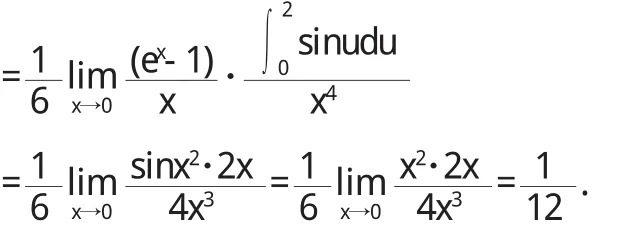
〔1〕同濟大學數學教研室.高等數學(上冊)[M].北京:高等教育出版社，1996.

〔2〕楊文泰，等.價無窮小量代換定理的推廣.甘肅高師學報，2005，10（2）：

〔3〕汪荷仙.高等數學解題方法指導[M].成都:成都科技大學出版社，1995.

O 13

A

1673-260X（2012）10-0007-03