集值映射空間與超空間的繼承稠密度和繼承Lindel?f度

楊春梅，李祖泉

（杭州師范大學(xué)理學(xué)院，浙江杭州310036）

集值映射空間與超空間的繼承稠密度和繼承Lindel?f度

楊春梅，李祖泉

（杭州師范大學(xué)理學(xué)院，浙江杭州310036）

利用連續(xù)集值賦值映射和弱拓?fù)溆懻摿思涤成淇臻g的繼承稠密度和繼承Lindel?f度，獲得了點態(tài)收斂拓?fù)淇臻g（X）上hd（（X））和hl（（X））與基本空間X的對偶性以及緊開拓?fù)淇臻g（X）上hd（X））和hl（X））與基本空間X的對偶性，推廣了單值連續(xù)集值映射空間（X）的相關(guān)結(jié)論.

集值映射空間；超空間；繼承稠密度；繼承Lindel?f度；弱拓?fù)?/p>

0 引 言

Zenor P［1］和McCoy R A［2-3］對函數(shù)空間（X）在賦予緊開拓?fù)湎碌睦^承稠密度和繼承Lindel?f度進(jìn)行了系統(tǒng)研究，騰輝，林壽［4］對點態(tài)收斂函數(shù)空間Cp（X）給出了繼承稠密度和繼承Lindel?f度的等價刻畫，并且指出了McCoy R A的證明中的錯誤.本文研究了點緊連續(xù)集值映射空間（X）和（X）與基本空間X和的繼承稠密度和繼承Lindel?f度的對偶不等式定理，給出了（X）上hd（（X））和hl（X））以及（X）上hd（k（X））和hl（X））的兩個對偶性證明.

本文中，拓?fù)淇臻gX是Hausdorff空間，K（X）表示X的所有非空緊子集族，ω表示可數(shù)序數(shù)，?表示自然數(shù)集，?表示實直線，（X）為X到?上的所有點緊致的連續(xù)映射族，p（X）為（X）賦予點態(tài)收斂拓?fù)洌琸（X）為（X）賦予緊開拓?fù)?文中未定義的術(shù)語和符號均以［3］，［5］和［6］為準(zhǔn).

1 預(yù)備知識

對于X的子集K，?的子集U，V，記W＋［K；U］＝｛f∈k（X）：f（K）?U｝；W-［K；V］＝｛f∈k（X）：f（x）∩V≠φ，x∈K｝.

定義1 以所有形如W＋［x；U］，W-［x；V］的集為子基作為（X）的拓?fù)洌渲衳∈X，U，V為?的開子集.該拓?fù)浞Q為點態(tài)收斂拓?fù)洌洖閜（X）.

定義2 以所有形如W＋［K；U］，W-［K；V］的集為子基作為（X）的拓?fù)洌渲蠯∈K（X），U，V為

的集生成，其中K∈K（X），k∈?，V1，V2，…，Vk為?中的開集.證明 由定義，k（X）的基開集由形如W＋［K，U］，W-［K，V］的集的有限交

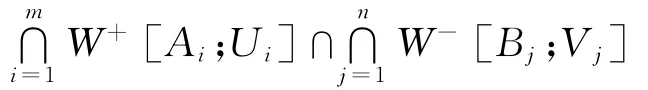
生成，其中Ai，Bj∈K（X），開集Ui，Vj??，1≤i≤m，1≤j≤n，m，n∈?.容易證明∩mi＝1W＋［Ai；Ui］∩∩nj＝1W-［Bj；Vj］＝∩mi＝1W［Ai；Ui］∩∩nj＝1W［Bj；Vj，X］.另一方面，對于任意K∈K（X），開集Vi??，1≤i≤k，k∈?，W［K；……