一道自主招生試題的探究與推廣

☉江蘇省高郵市第二中學(xué) 于海軍

一、提出問(wèn)題

2011年北大等十三校聯(lián)考（北約）自主招生考試數(shù)學(xué)試卷的壓軸題是：

求|x-1|+|2x-1|+|3x-1|+…+|2011x-1|的最小值.如何求？

二、探究思路

A.190 B.171 C.90 D.45

這是2006年全國(guó)高考題.處理這類含絕對(duì)值的最值問(wèn)題主要有兩種途徑：（1）利用絕對(duì)值的幾何意義借助三角不等式|a|+|b|≥|a±b|；（2）利用絕對(duì)值零點(diǎn)分段討論作函數(shù)的圖像.

解法一：|x-1|+|x-19|=|x-1|+|19-x|≥19-1，當(dāng)且僅當(dāng)x∈［1，19］時(shí)取等號(hào)|x-2|+|x-18|=|x-2|+|18-x|≥18-2，當(dāng)且僅當(dāng)x∈［2，18］時(shí)取等號(hào)|x-3|+|x-17|=|x-3|+|17-x|≥17-3，當(dāng)且僅當(dāng)x∈［3，17］時(shí)取等號(hào)

……

|x-9|+|x-11|=|x-9|+|11-x|≥11-9，當(dāng)且僅當(dāng)x∈［9，11］時(shí)取等號(hào)

|x-10|≥0，當(dāng)且僅當(dāng)x=10時(shí)取等號(hào).

而x=10∈［9，11］?［8，12］?［7，13］…?［1，19］

故當(dāng)x=10時(shí)，上述各不等式中的等號(hào)同時(shí)成立.

所以f（x）的最小值為f（10）=9+8+7+…+2+1+1+2+…+9=90.選C.

解法二：當(dāng)x∈（-∞，1］時(shí)，f（x）=（1-x）+（2-x）+…+（19-x）=1+2+3+…+19-19x.

當(dāng)x∈（1，2］時(shí)，f（x）=（x-1）+（2-x）+…+（19-x）=-1+2+3+…+19-17x.

當(dāng)x∈（2，3］時(shí)，f（x）=（x-1）+（x-2）+…+（19-x）=-1-2+3+…+19-15x.

……

當(dāng)x∈（9，10］時(shí)，f（x）=（x-1）+（x-2）+…（x-9）+（10-x）+…+（19-x）=-1-2-3-…-9+10+…+19-x.

當(dāng)x∈（10，11］時(shí)，f（x）=（x-1）+（x-2）+…+（x-9）+（x-10）+（11-x）+…+（19-x）=-1-2-3-…-9-10+11+…+19+x

……

當(dāng)x∈（19，+∞）時(shí)，f（x）=（x-1）+（x-2）+…+（x-19）=-1-2-3-…-19+19x.

可見(jiàn)，f（x）的圖像為：兩側(cè)是向上無(wú)限伸展的射線，中間是首尾相連的線段，各段從左到右斜率依次增加.到x∈（9，10］時(shí)仍為減函數(shù)，而從x∈（10，11］時(shí)起為增函數(shù)，故f（x）在x=10時(shí)取最小值，f（10）=9+8+7+…+2+1+1+2+…+9=90.選C.

證明：（1）當(dāng)n=2k-1（k∈N+）時(shí)，f（x）=|x-a1|+|x-a2|+|x-a3|+…+|x-a2k-2|+|x-a2k-1|a1

|x-a2|+|x-a2k-2|≥|（x-a2）+（a2k-2-x）|=a2k-2-a2，當(dāng)且僅當(dāng)x∈［a2，a2k-2］時(shí)取等號(hào).

……

|x-ak-1|+|x-ak+1|≥|（x-ak-1）+（ak+1-x）|=ak+1-ak-1，當(dāng)且僅當(dāng)x∈［ak-1，ak+1］時(shí)取等號(hào).

|x-ak|≥0，當(dāng)且僅當(dāng)x=ak時(shí)取等號(hào).

由于ak∈［ak-1，ak+1］?［ak-2，ak+2］?…?［a2，a2k-2］?［a1，a2k-1］

從而當(dāng)且僅當(dāng)x=ak時(shí)上述各不等式同時(shí)取等號(hào)，所以f（ak）為最小值，其中

（2）當(dāng)n=2k（k∈N+）時(shí)，f（x）=|x-a1|+|x-a2|+|x-a3|+…+|x-a2k-1|+|x-a2k|.

a1

|x-a1|+|x-a2k|≥|（x-a1）+（a2k-x）|=a2k-a1當(dāng)且僅當(dāng)x∈［a1，a2k］時(shí)取等號(hào).

|x-a2|+|x-a2k-1|≥|（x-a2）+（a2k-1-x）|=a2k-1-a2，當(dāng)且僅當(dāng)x∈［a2，a2k-1］時(shí)取等號(hào).

……

|x-ak|+|x-ak+1|≥|（x-ak）+（ak+1-x）|=ak+1-ak當(dāng)且僅當(dāng)x∈［ak，ak+1］時(shí)取等號(hào).

由于［ak，ak+1］?［ak-1，ak+2］?…?［a2，a2k-1］?［a1，a2k］，

故當(dāng)x=t∈［ak，ak+1］時(shí)，上述各不等式同時(shí)取等號(hào)，所以f（x）在x=t時(shí)取最小值，其中

引例2求f（x）=|x-1|+3|x-2|+4|x-3|+5|x-4|的最小值.

分析：f（x）=|x-1|+|x-2|+|x-2|+|x-2|+|x-3|+|x-3|+|x-3|+|x-3|+|x-4|+|x-4|+|x-4|+|x-4|+|x-4|，共有1+3+4+5=13項(xiàng)，不妨設(shè)為

f（x）=|x-a1|+|x-a2|+|x-a3|+…+|x-a13|，其中a1=1，a2=a3=a4=2.

a5=a6=a7=a8=3，a9=a10=a11=a12=a13=4，并且中間項(xiàng)為|x-a7|，a7=3.

故f（x）的最小值為f（3）=2+3+5=10.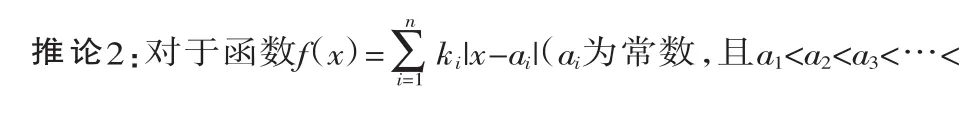

三、解決問(wèn)題