《幾何畫板》的應用價值之我見
☉河南省固始縣慈濟高中 吳 強
當前,踐行“科學發展觀”已成時代主題.在這個信息技術日新月異的時代,教師應時刻思考用先進技術手段改進教學方法,并發展、升華教育思想,實現教育教學的科學發展.《幾何畫板》作為一款優秀的教學軟件,雖然早已面世,但很多教師出于認識或條件所限,并未將其真正應用于教學.本文著重介紹筆者在教學中應用該軟件的心得和收獲,以期引起思索和共鳴,并讓更多同仁投身于教改和信息技術應用中來.
形象思維在學習和研究中都起著重要作用,一個學生如果不具備良好的數學形象思維能力,不可能學好數學.數學家柯爾莫哥洛夫曾說:“只要有可能,數學家總是盡力把他們正在研究的問題從幾何上視覺化.”因此,隨著信息技術的發展并廣泛應用于各個領域,也給課堂教學帶來了深刻變革——用計算機輔助教學,改善學生的認知環境已成為必然趨勢.《幾何畫板》以其門檻不高和操作方便的優點,及強大的圖形處理能力、易用的動畫功能被國內外專家、教師推崇,并成為制作數學課件的主流軟件之一.其應用價值主要體現在以下方面.
一、《幾何畫板》讓代數教學圖形化、直觀化
“數形結合”一直是高中數學中的一個重要思維方法,而對其運用最廣泛的莫過于函數部分.“函數”的思維和分析方法滲透在高中數學的各個章節;同時,函數是以運動、變化的觀點對現實世界數量關系作出刻畫,這又決定了它是對學生進行素質教育的重要載體.函數的兩種表達方式——解析式和圖像之間常常需要比照、融合(如研究函數的單調性、討論方程或不等式的解的情況等).在函數的傳統教學中,教師多用手工繪圖,但手工繪圖有不精確、效率低的弊端.而應用《幾何畫板》精準直觀的展示及變化功能則可以克服上述弊端,大大提高教學效果和課堂效率,起到事半功倍的效果.
例如,利用《幾何畫板》作圖功能,在同一個直角坐標系中作出函數y的圖像,通過各自圖像特點,比較其位置和變化規律,歸納冪函數的性質.同時《幾何畫板》還可以作出含有若干參數的函數圖像,當參數變化時函數圖像也相應地變化,如在講函數y=Asin(ωx+φ)的圖像時,傳統教學只能將A、ω、φ代入有限個值,觀察各種情況的函數圖像之間的關系;而利用《幾何畫板》則可以以線段b、T的長度和A點到x軸的距離為參數作圖(如圖1),當拖動兩條線段的某一端點(即改變兩條線段的長度)時分別改變三角函數的初相和周期,拖動點A則改變其振幅,達到動態演示.這樣在教學時既快速靈活、形象直觀,又不失一般性.
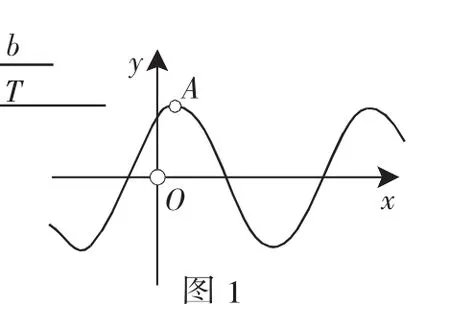
二、《幾何畫板》讓立體幾何教學更加高效、精準
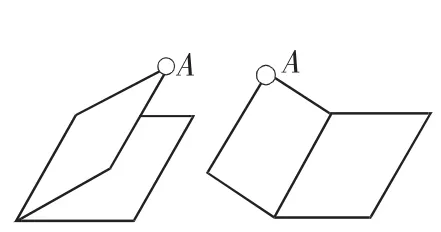
圖2
立體幾何是在平面圖形分析的基礎上討論空間圖形的性質.從平面觀念過渡到立體觀念,無疑是認識上的一次飛躍.初學立體幾何時,大多數學生不具備豐富的空間想象力及較強的平面到空間的圖形轉化能力,這給學生學習立體幾何增加了困難.而應用《幾何畫板》將圖形動起來,就可以使圖形中各元素之間的位置比照和度量關系惟妙惟肖,能讓學生從多個不同的角度去觀察圖形.這樣,不僅可以幫助學生理解和接受立體幾何知識,還可以讓學生的想象力和創造力得到充分的發揮.
像在講二面角的定義時(如圖2),當拖動點A時,點A所在的半平面也隨之轉動,改變了二面角的大小.生動直觀的圖形變動有利于幫助學生建立空間思想和培養空間想象力;在演示用祖暅原理推導球體積公式時,運用動畫和
軌跡功能作圖3,過O作球和柱、錐的水平截面,當上下拖動點O時,讓學生觀察此過程中兩個幾何體相應截面的變化規律和內在聯系,并在預習教材的基礎上論證所截得的兩截面面積之和為定值,進而自主應用祖暅原理推導出球體積公式.這樣的教學設計能讓學生產生濃厚興趣和強烈求知欲,同時美麗生動的畫面在學生學得知識的同時,給人以美的感受,創建一個輕松、樂學的氛圍.
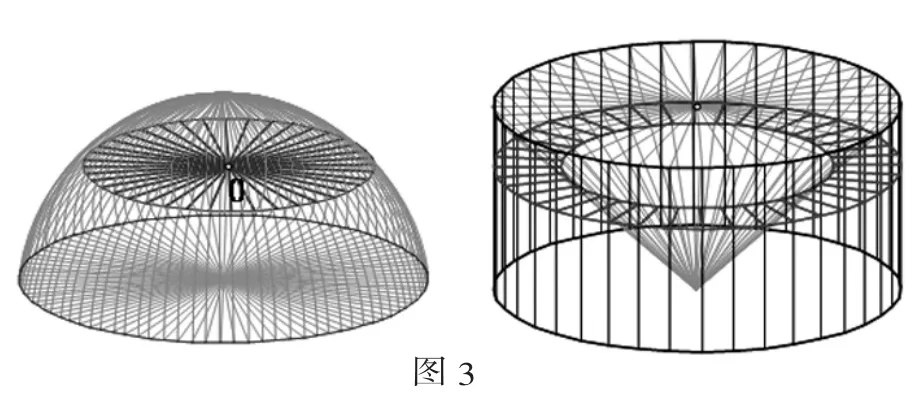
三、《幾何畫板》讓平面解析幾何更加生動形象
平面解析幾何是用代數方法來研究幾何問題的一門數學學科,展示幾何圖形變化與運動的動態過程在解析幾何教學中是非常重要的.《幾何畫板》又以其極強的運算功能和圖形分析處理功能在解析幾何中大顯身手.比如它能作出各種形式的方程(普通方程、參數方程、極坐標方程)的曲線;能對動態的對象進行“追蹤”,并顯示該對象的“軌跡”;能通過拖動某一對象(如點、線)觀察整個圖形的變化來研究兩個或兩個以上曲線的位置關系.
例如在講橢圓的定義時,可以由“到兩定點F1、F2的距離之和為定值的點的軌跡”入手——如圖4,在幾何畫板上令線段AB的長為“定值”,在線段AB上取一點E,再分別以F1為圓心、AE的長為半徑和以F2為圓心、BE的長為半徑作圓.然后拖動點E,使得兩圓半徑隨之變化但半徑和為定值,大家可以自主發現兩圓的交點軌跡即符合要求的研究對象.
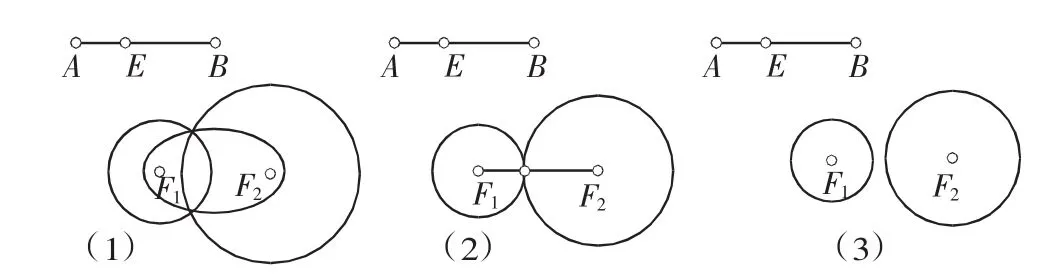
圖4
先讓學生猜測這樣的點的軌跡是什么圖形,學生各抒己見之后,老師動態演示圖4(1),學生豁然開朗:“原來是橢圓!”.這時老師用鼠標拖動點B(即改變線段AB的長),使得|AB|=|F1F2|,如圖4(2),滿足條件的點的軌跡變成了一條線段F1F2,學生開始謹慎起來并主動思索,接下來不難得出圖4(3)(|AB|<|F1F2|時)的情形,隨后請大家自主歸納這三類情況之間的區別與聯系.經過上述過程,學生不僅深刻地掌握了橢圓的概念,也鍛煉了其思維的縝密性,強化了分類思想.
綜上所述,使用《幾何畫板》進行數學教學,通過形象的感性信息呈現,給學生留下更為深刻的印象,使學生不再是把數學作為單純的知識去理解記憶,而是能夠更有實感地去體會、把握.這樣,既能激發學生的情感、培養學生的興趣,又能大大提高課堂效率,取得良好教學效果.
1.姚淑華,李孝誠.《幾何畫板在中學數學教學中應用模式的探討》.《電腦知識與技術》,2008年30期.
2.陶維林.《幾何畫板實用范例教程(第2版)》,清華大學出版社出版,2008-07-01.

