部附件送修費用的偏最小二乘回歸模型及敏感性分析

王卓健， 饒學軍， 沈安慰， 賈林通

(1.空軍工程大學航空航天工程學院，西安 710038; 2.西安飛機工業(集團)有限公司技術中心，西安 710089)

0 引言

長期以來，飛機維修費用的估算是熱點也是難點。維修費用涉及因素復雜，持續時間長，使得在飛機壽命周期費用中，維修費用是其主要構成成分［1］。根據WATOG(World Airline Technical Operations Glossary)對維修費用的劃分標準，可分為直接維修費用和間接維修費用，間接維修費用由于與管理因素有關，難以在設計階段考慮。

目前，國內外研究主要集中在直接維修費用上，已經形成了一些方法和體系［2］。國外已經有較為成熟的壽命周期費用估算軟件，最具有代表性的當屬PRICE(Parametric Review of Information for Costing and Evaluation)，它在國外應用中取得了較好的效果［3］。但是，由于國內與國外在經濟體制、費用發生狀況上有較大區別，完全照搬并不適合我國國情。利用目前掌握的數據，開發出一套適合國情的費用模型已勢在必行。部附件的送修費用在整個直接維修費用中占有基礎性地位并且費用數據相對透明，因此構建部附件送修費用模型不失為一個好的突破口。在部附件送修費用模型中，較為著名的是波音的可信性成本(DCM)模型［4］和空客公司的模型。這兩種模型所需的輸入數據涉及到人工時費用和材料費用，這些數據很難在國內收集到。文獻［5］針對這兩種模型在國內應用的難點，提出了基于免疫粒子群算法的組合預計，但是此模型的輸入參數是通過某些設計性能參數估算得出，數據的準確性不能保證。同時，由于其組合模型的“黑匣子”特性，與其他一些智能預測方法，如神經網絡［6］，支持向量機［7］等一樣，雖然預測精度較高，但同樣存在不方便進行敏感性分析的缺點。偏最小二乘回歸由于在處理小樣本多元數據具有優越性，并且能方便進行敏感性分析，已經應用到機體研制費的估算上，取得了較好的效果［8］。本文針對目前國內數據特點提出了一種基于偏最小二乘回歸的部附件送修費用的參數模型，并進行了敏感性分析。

1 數據收集與處理

全壽命費用的定量研究方法主要有類比法、工程估算法、參數法，其中參數法的研究最為廣泛和流行［9］。要建立一個較好的參數模型，首先根據可收集到的數據，包括各種參數數據和費用數據，篩選出與費用關系密切的參數;其次，利用一種建模理論，建立費用與參數之間的函數關系。其中關鍵在于所收集數據的準確性，本文收集到了某型飛機20種部附件的數據，包括有重量(W)、體積(V)、價格(P)、平均非計劃拆卸時間(TMTBUR)，平均車間修理時間(TST)，SRU的個數(NSRU)以及送修費用(PS)等，如表1所示。

表1 部附件參數與送修費用Table 1 Parameters and repair cost of components

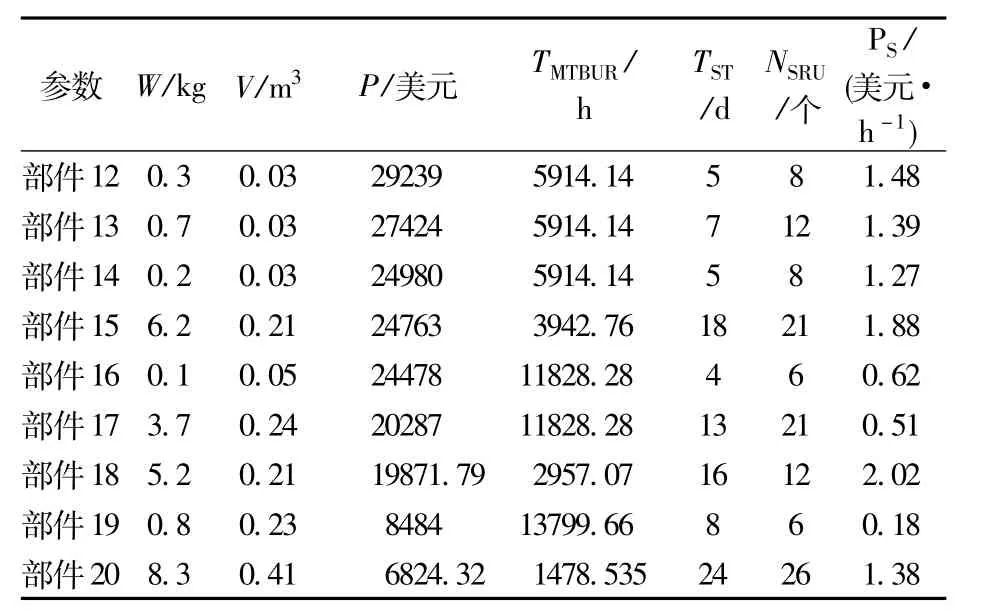
續表

2 變量投影重要度分析

基于表1，可選取偏最小二乘回歸［10］來建立參數模型。首先篩選參數，常用的方法有相關關系分析、變量逐步回歸法等，這些方法在小樣本情況下面臨新的困難，而基于偏最小二乘回歸的變量投影重要度分析是一種有效方法。

根據文獻［10］，可以做如下表述。參數對因變量的解釋能力是以變量投影重要性指標Pj(Variable Importance in Projection)來測度的。其定義式為

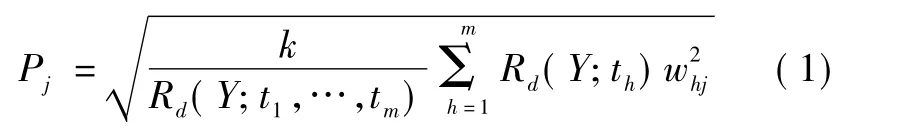
式中:whj為軸wh的第j個分量，用于衡量xj對構造th主成分的貢獻大小;Rd(Y;th)和 Rd(Y;t1，t2，…，tm)分別為Y由th和t1，t2，…，tm所解釋的變異精度(測定系數)，分別代表了th對Y的解釋能力和t1，t2，…，tm對Y的累計解釋能力。

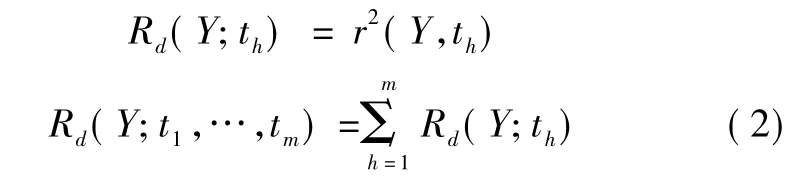
式中，r(Y，th)是因變量Y和主成分th的相關系數。

Pj定義式的意義是基于這樣一個事實:由于xj對Y的解釋是通過th來傳遞的，如果th對Y的解釋能力很強，而xj在構造th時又起到了相當重要的作用，則xj對Y的解釋能力就被視為很大。也就是說，如果在Rd(Y;th)值很大的th成分上，whj取很大的值，則xj對解釋Y就有很重要的作用。

另外，因為有

所以，對于k個參數xj(j=1，2，…，k)，如果在解釋 Y時的作用都相同，則所有的Pj均等于1;否則，對于Pj＞1的xj，在解釋Y時就有更加重要的作用。

根據式(1)～式(3)，將重量、體積、價格、平均非計劃拆卸間隔時間、平均車間修理時間、SRU的個數當作參數，將送修費用作為因變量，提取一次主成分，計算其變量投影重要度，得到結果如表2所示。

表2 6個參數的變量投影重要度Table 2 The VIP of six parameters

從表2可以看出，體積的變量投影重要度值過于偏小，因此可以刪除體積重新計算各個參數的變量投影重要度，如表3所示。

表3 5個參數的變量投影重要度值Table 3 The VIP of five parameters

從表3可以看出，沒有變量投影重要度值明顯偏小的參數，且比較均衡，因此保留現有5個參數。

3 偏最小二乘回歸模型

采取文獻［10］的建模方法，選取重量、價格、平均非計劃拆卸間隔時間、平均車間修理時間、SRU的個數為參數開始偏最小二乘回歸建模。采用對數線性關系式，取第一主成分，此時變量投影重要度較為均衡，擬合公式為

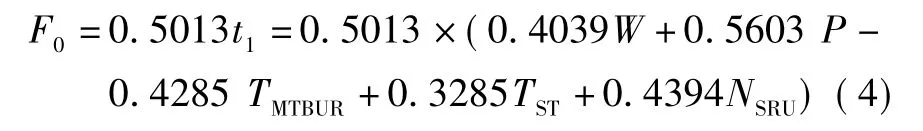
當給定顯著性水平 α為0.01，t檢驗的值 T為1.0577，接受 t檢驗;當假設檢驗參數 F 為 1.9578，接受F檢驗。將式(4)進一步作標準化的逆過程，則可以得到

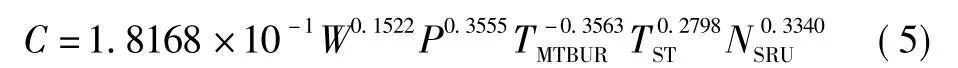
式(5)的平均誤差為3.53%，不需要進行第二主成分的提取。誤差如圖1所示。

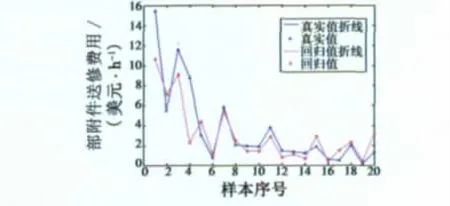
圖1 真實值與回歸值的誤差Fig.1 The error of the true number and regression number

4 部附件維修費用敏感性分析

得到了部附件送修費用的偏最小二乘回歸模型后，可以方便進行費用敏感性分析。在工程設計時要求部附件送修費用最小，則重量、價格、平均車間修理時間、SRU的個數是越小越好，平均非計劃拆卸間隔時間越大越好。根據工程經驗，假設其參數的取值范圍如表4所示。

表4 5個參數的取值范圍Table 4 The range of five parameters

在各個參數值由最差值向最優值逼近的過程中，設計人員最為關心的是費用變化最為敏感的區間。當重量W變化時，其他參數值保持最差值不變時，其重量與部件送修費用的單一函數為

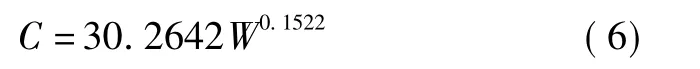
其重量與部附件送修費用變化曲線如圖2所示。

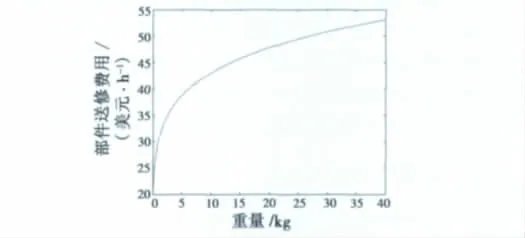
圖2 重量與送修費用關系Fig.2 The relation of weight and repair cost

敏感度實質上就是重量與費用關系曲線上各個點的切線斜率，根據切線曲率即為單一函數一階導數的事實，對式(6)求一階導數

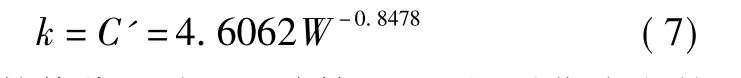
將重量的數值代入式(7)計算，可以得到曲線在某一點上的切線斜率，即為敏感度。在重量與送修費用的敏感度分析中，重量由最差值(40)向最優值(0)逼近的過程中(步長單位選擇為0.1)，敏感度在［0.2019+∞］之間變化。重量與敏感度的關系曲線如圖3所示。

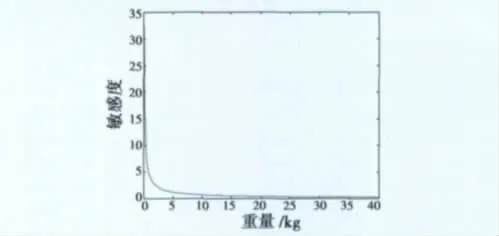
圖3 重量與敏感度關系Fig.3 The relation of weight and sensitivity

本文認為對于重量而言，敏感度大于1時，即屬于顯著敏感性區間。同理可以得到其他參數對應的送修費用單一函數表達式，顯著敏感性區間以及所對應參數范圍，如表5所示。

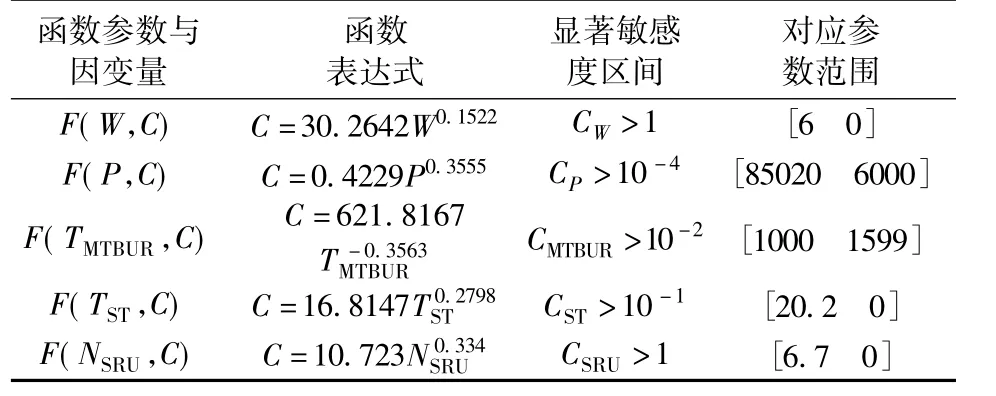
表5 顯著敏感性區間以及所對應參數范圍Table 5 The salient sensitive interval and the range of parameter

價格、平均非計劃拆卸間隔時間、平均車間修理時間、SRU的個數與敏感度之間的關系曲線如圖4～圖7所示。

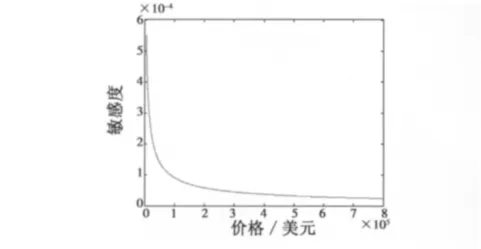
圖4 價格與敏感度關系Fig.4 The relation of price and sensitivity

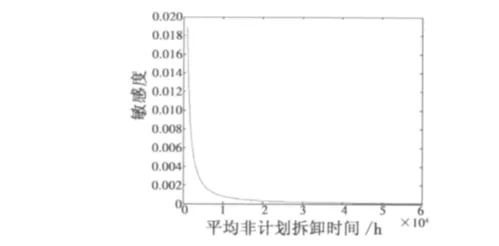
圖5 平均非計劃拆卸間隔與敏感度關系Fig.5 The relation of MTBUR and sensitivity

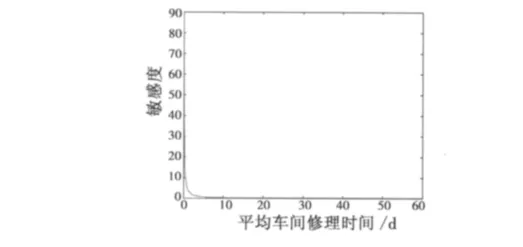
圖6 平均車間修理時間與敏感度Fig.6 The relation of the mean shop repair time and sensitivity

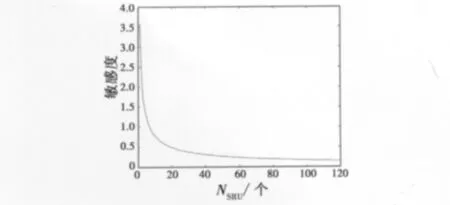
圖7 SRU數量與敏感度Fig.7 The relation of the number of SRU and sensitivity

5 結論

本文根據所收集到的某型飛機部附件的參數及送修費用數據，建立了基于重量、價格、平均非計劃拆卸間隔時間、平均車間修理時間、SRU的個數為參數的部件送修費用偏最小二乘回歸模型，模型平均誤差小于5%，由于采取了對數線性表達式，復雜程度大大降低，完全可滿足工程實踐的需要，結合模型，利用切線斜率的物理意義詳細計算了單一函數模型的顯著敏感性的區間。計算表明，顯著敏感性區間與參數的最差值和最優值有較強的相關性。需要特別注意的是計算敏感度時，每個參數在工程實際中遞增或遞減的單位量級(如價格變化的單位是100美元還是1000美元，可能不同的部件并不完全相同)，此問題并沒有在文中探討，需要進一步的實際數據支持和研究。

［1］ 張恒喜，郭基聯，董彥非，等.現代飛機效費分析［M］.北京:航空工業出版社，2001.

［2］ 陳勇.民用飛機維修成本分析與評估［D］.南京:南京航空航天大學，2006.

［3］ 郭基聯，虞健飛，任建軍.裝備壽命周期費用估算軟件PRICEH 剖析［J］.裝備指揮學院學報，2009，20(4):22－26.

［4］ MEADOWS T A.Analysis of F/A －18 engine maintenance costs using the boeing dependability cost model［M］.Washington:Naval Postgraduate School Monterey，California，1994.

［5］ 吳靜敏.民用飛機全壽命維修成本控制與分析關鍵問題研究［D］.南京:南京航空航天大學，2006.

［6］ 郭風，李登科，張恒喜，等.軍用無人機研制費用的RBF神經網絡預測［J］.電光與控制，2005，12(6):60－62.

［7］ 鐘詩勝，付旭云，胡淑榮.小樣本條件下航空裝備費用預測［J］.哈爾濱工業大學學報，2011，43(5):52－55.

［8］ 王禮沅，郭基聯，張恒喜.遞階偏最小二乘回歸在飛機研制費用預測中的應用［J］.航空學報，2009，30(8):1380－1384.

［9］ 孟科，張恒喜，段經緯，等.基于未確知數理論的裝備全壽命費用定性估算方法［J］.電光與控制，2005，12(6):66－69.

［10］ 王慧文，吳載斌，孟潔.偏最小二乘回歸的線性與非線性方法［M］.北京:國防工業出版社，2006.