例析勾股定理的應用

☉江蘇南通市通州區(qū)興仁中學 張玉娟

勾股定理揭示了直角三角形中三邊之間的數量關系，幾何中的很多計算問題都可轉化到直角三角形中，用勾股定理來解決.圍繞著勾股定理，出現了許多形式新穎，內容豐富的新型試題，這些新題，既考查了對勾股定理的理解、掌握和運用，又考查了同學們的創(chuàng)新能力.現采擷幾道典型試題，進行分類說明，供大家參考.

一、利用勾股定理求面積

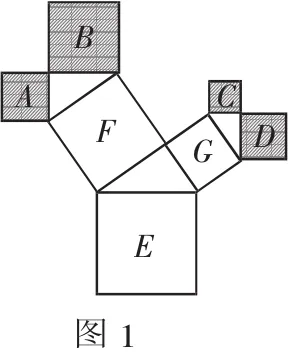
例1 如圖1是一株美麗的勾股樹，其中所有的四邊形都是正方形，所有的三角形都是直角三角形.若正方形A、B、C、D的面積分別是3、5、2、3，則最大正方形E的面積是（ ）.

A.13 B.26 C.47 D.94

解析：因為勾股樹中每相鄰的三個正方形圍成一個直角三角形，所以正方形A、B邊長的平方和等于正方形F的邊長的平方，即正方形A與正方形B的面積之和等于正方形F的面積，從而正方形F的面積為8；同理可得正方形G的面積為5；再利用上述結論，正方形E的面積等于正方形F和G的面積之和，故選擇A.

評注：解決這類題的關鍵是抓住題目的特征，找出本題圖形中的隱藏規(guī)律：如果把大正方形作為第一層，兩個小正方形作為第二層，那么第二層的兩個小正方形的面積之和等于第一層正方形的面積.

二、利用勾股定理求最短距離

例 2 如圖2，長方體的長為15，寬為10，高為20，點B離點C的距離為5，一只螞蟻如果要沿著長方體的表面從點A爬到點B，需要爬行的最短距離是（ ）.

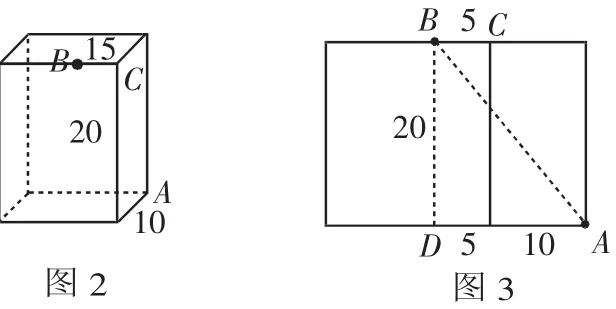
解析：因為螞蟻從A到B點沿著長方體的表面爬行，因此將長方體側面展開成平面圖形，右圖3是展開圖的一部分，其中過B點作對邊的垂線段，得到BD=20；由題意可知AD=15.根據“兩點之間，線段最短”得A點到B點的最短距離為AB的長，在 Rt△ABD 中，∠ADB=90°，由勾股定理得：BD2+AD2=AB2，解得AB=25.即從A點到B點的最短距離為25，故選擇B.

評注：求立體圖形表面上兩點間的最短距離，一般情況下，是將立體圖形展開成平面圖形，然后構造直角三角形，利用勾股定理去解答.

三、利用勾股定理求事件的概率

例3“趙爽弦圖”是四個全等的直角三角形與中間一個小正方形拼成的大正方形.如圖4，是一“趙爽弦圖”飛鏢板，其直角三角形的兩條直角邊的長分別是2和4.小明同學距飛鏢板一定距離向飛鏢板投擲飛鏢（假設投擲的飛鏢均扎在飛鏢板上），則投擲一次飛鏢扎在中間小正方形區(qū)域（含邊線）的概率是（ ）.

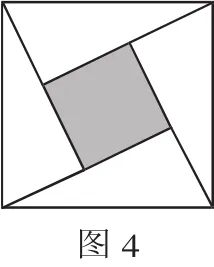
解析：這是典型的弦圖，我們很容易得出中間陰影部分是一個正方形，而且邊長為2；再根據勾股定理求出大正方形的邊長為.因為所有正方形都有相似性，所以本圖中小正方形與大正方形的面積比為對應邊的比的平方，即1∶5；再根據概率公式求出投擲一次飛鏢扎在中間小正方形區(qū)域（含邊線）的概率是，故選擇C.

評注：本題是集勾股定理、三角形、四邊形、相似的性質、概率等為一體的綜合題，考查比較全面.

四、利用勾股定理求圓的直徑

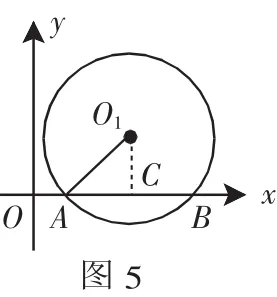
例4 如圖5，已知⊙O1與坐標軸交于 A（1，0）、B（5，0）兩點，點 O1的縱坐標為.求⊙O1的半徑.

解析：過點O1作O1C⊥AB，垂足為C，則有AC=BC.

由 A（1，0）、B（5，0），得 AB=4，則 AC=2.

在Rt△AO1C中，O1的縱坐標為

所以⊙O1的半徑

評注：本題考查求平面直角坐標系中點的坐標，以及垂徑定理的應用，要求利用勾股定理去求圓的直徑.

五、用勾股定理測河寬

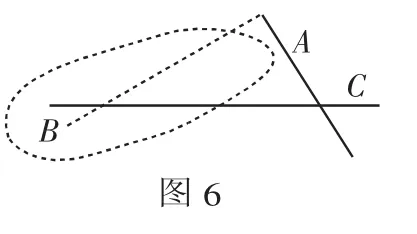
例5 如圖6，陰影表示長江宜昌段某處的江面部分，為了測量A、B兩點之間的距離，觀察者確定三個測點 A、B 和 C，分別測∠BAC=90°，又量得BC=1300m，AC=500m，于是，他們可計算A、B之間的距離.

解析：本題是應用勾股定理解決實際問題.

由測量可知：∠BAC=90°，直角邊AC=500m，斜邊BC=1300m.根據 AB2=BC2-AC2，得：

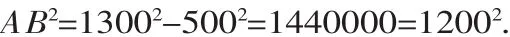
所以AB=1200m.

評注：本題是勾股定理的實際應用，考查實際生活中不能夠直接測量的地方.構造直角三角形，利用勾股定理求出兩點之間的距離.

六、用勾股定理量物高

例6 有這樣一段古詩和圖片：“如圖7，今有竹高一丈，末折抵地，去本三尺.問折者高幾何.”請你回答這首詩里提出的問題.寫出解答這首詩的方法和步驟.

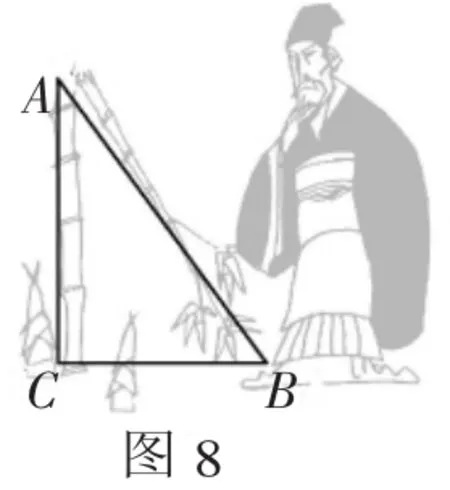
解析：根據詩里所描述的情景，把它轉化為數學問題，畫出圖8.

則原處還有4.55尺高的竹子.

評注：本題是古代有趣的勾股定理應用題，同時也是一道實際生活應用題，考查了同學們建模的思想方法.

七、用勾股定理求周長

例7 有一塊直角三角形的綠地，量得兩直角邊長分別為6m、8m，現在要將綠地擴充成等腰三角形，且擴充部分是以8m為直角邊的直角三角形，求擴充后等腰三角形綠地的周長.

解析：在 Rt△ABC 中，∠ACB=90°，AC=8，BC=6，由勾股定理知AB=10.擴充部分為Rt△ACD，擴充成等腰△ABD，應分為以下三種情況：

①如圖9，當AB=AD=10時，可求得CD=CB=6，則△ABD的周長為32m.

②如圖10，當AB=BD=10時，可求得CD=4，由勾股定理得：

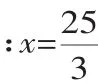
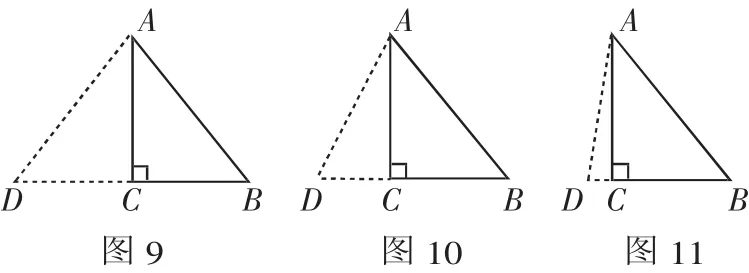
評注：本題既考查勾股定理的應用，又考查等腰三角形的性質，同時比較全面地考查同學們分類討論思想的掌握情況.

總之，勾股定理已有數千年的歷史，在古代、當今和未來都有廣泛的應用.勾股定理在實際中應用非常廣泛，與實際生活聯系密切.在解決實際問題時，關鍵是把實際問題的量轉化為直角三角形的三邊，從而使用勾股定理來解決.