初中數學教學中應用探究式教學模式探討

☉廣東佛山市獅山鎮官窯第二初級中學 潘麗歡

初中數學教學中應用探究式教學模式探討

☉廣東佛山市獅山鎮官窯第二初級中學 潘麗歡

探究式教學模式給學生提供了更多的數學交流機會，有利于促進學生思維、語言、個性等多方面發展.探究式教學用開放的問題激發學生探究的興趣，靈活運用數學基礎知識和技能、解題模式、數學方法的典范，啟迪學生的思維.

一、將教學內容設計成適宜學生探究的形式

我們在設計數學內容的呈現方式時，注重考慮如何有利于學生主動參與到各種形式（觀察、實驗、猜想、驗證、推理、交流等）的數學活動中，并能照顧到各階段學生不同的知識背景和認知水平；注重考慮如何真正從學生是數學學習的主人出發，充分考慮其主體性的發揮，并更多地通過合作所產生的互動效應促使每個學生都能經歷自主探索與交流的過程.比如，在創設問題情境引發探究興趣方面，我在講全等三角形的判定的復習課中，可創設這樣的問題情景：如果有兩個三角形，它們有兩條邊和一個角對應相等，這樣的兩個三角形全等嗎？會有很多同學回答全等.然后教師出示圖形（如圖1）：△ABC 和 △ABD 中 ，AB=AB，BC=BD，∠A公共角，很明顯兩個三角形不全等.此時，學生不禁會問：我們不是學過邊角邊（SAS）判定兩個三角形全等嗎？為什么現在又不全等呢？有兩條邊和一個角對應相等的兩個三角形在什么情況下才全等呢？設置了一個“障礙”情景，這一“障礙”情景的創設在學生的大腦里立即產生了碰撞，思維被迅速地激活起來，此時，學生會產生強烈的求知欲望，進而使學生獲得對數學理解的同時，在思維能力、情感態度與價值觀等方面都得到發展.教學設計與具體組織教學滲透了新課程的教學理念和創新教育的思想.

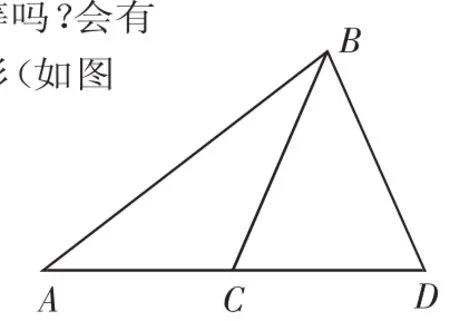
圖1

二、注重培養學生的觀察能力

數學中的觀察是對數學問題或對象的屬性特征通過視覺獲取信息，運用思維辨認其形式、結構和數量關系，從而發現規律或本質的方法.創造性思維活動通常都是從觀察開始.觀察是通向創新的橋梁.從觀察入手，從特征中發現知識的內在聯系.例如，在《平行線》這一節課中，教師可通過讓學生觀察“生活中（如教室、操場等）的平行線”；畫平行線（有格子或用三角板）；使用幻燈片讓學生觀察等；從而引出“過直線外一點有且只有一條直線與已知直線平行”；“平行于同一直線的兩條直線互相平行”.

觀察與實驗是歸納、類比、想象等思維活動的基礎，它為思維活動提供感性材料，包含對數學問題的精密細致的考察，以及積極合理的思索，觀察是一種有目的、有計劃的收集題目信息并伴隨著積極思維的過程.

三、加強問題的變式、引申與推廣，培養學生發現創新的能力

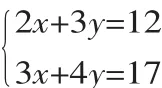
從而對方程組進行變式、引申和推廣，一式變用、一題多解變式、一題多變等，以達到培養學生的探索能力.

四、加深拓展促進認知結構內化

在課堂教學中，對于同一個數學問題，不同認知水平的學生常常會有不同的反映.學生通過探究而獲得知識，可能有一些還是表面的、零散的，甚至是錯誤的.因此，組織全班學生的交流、評價，實現認知上的互相啟發和補充，深化對新知識的理解，促進認知結構內化過程，從而完成認知結構上的意義建構是非常必要的.例如，在“特殊平行四邊形”教學時，利用以下問題：（1）順次連接四邊形ABCD各邊中點，得到四邊形EFGH，問四邊形EFGH是什么四邊形？（2）要使四邊形EFGH為菱形，應對四邊形ABCD添加怎樣的條件？對所學知識進行鞏固.學生通過思考討論，在（2）反饋時，對若要使四邊形EFGH為菱形，有的說：四邊形ABCD應為矩形或正方形，有的說：四邊形ABCD應為等腰梯形，也有的說：應對四邊形ABCD添加條件AC=BD.這三個答案孰是孰非？各組學生據理力爭，其他學生也加入了熱烈的討論，最后公認：他們答案都正確，同時體會到了一般與特殊的關系.接著教師進一步引導：若要使四邊形EFGH為矩形、正方形，又要添加什么條件？教學生通過解決以上問題，就會得出四邊形的一些內在規律：

①當原四邊形的對角線相等時，順次連接四邊形四邊中點所得的四邊形是菱形.②當原四邊形的對角線垂直時，順次連接四邊形四邊中點所得的四邊形是矩形.③當原四邊形的對角線垂直且相等時，順次連接四邊形四邊中點所得的四邊形是正方形.教師應根據課堂教學時間密切關注學生的探究活動，及時了解學生學習的進展情況，把握探究節奏，充分發揮主導作用，采用多種形式，注重融知識性與趣味性于一體，讓學生在輕松活潑的氛圍中應用、拓展.

本文研究“探究型”課堂教學模式，旨在抓住數學學科特點，抓住學生具有創造和探究的潛能，通過教師的適當引導，學生用自己的學習方式去進行觀察比較，發現、提出問題，作出解決問題的猜想，嘗試解答并進行“驗證”的過程去揭示知識規律，求得問題的解決，充分發揮學生學習的自主性、主動性、創造性，從而真正把學習的自由還給學生，培養學生的自主探究能力，激發學生探求新知的愿望.