基于假定旋轉坐標的高速永磁同步電機無傳感器控制

紀 歷 徐龍祥

（南京航空航天大學機電學院 南京 210016）

1 引言

由電機驅動的風機、壓縮機等通用流體機械是石化、環保、冶金等領域廣泛應用的重要裝備，這類流體機械的轉速都比較高，需要增速箱和聯軸器，而且主要采用機械軸承。由增速箱、聯軸器和機械軸承造成功耗約占總驅動損失的 40%～50%。如果采用直驅式結構技術方案，將風機或壓縮機的葉輪直接裝在電機軸上，并采用磁懸浮軸承[1,2]，能夠節約能源7%～10%。此外，這些設備通常采用異步電機，其效率只有94% 左右。如果采用高速永磁同步電機[3,4]，效率可達 97% 左右。因此，采用磁懸浮軸承支承的高速永磁同步電機成為近年來的研究熱點之一。為了提高輕載及升速時的運行效率，永磁同步電機通常采用閉環控制，這就需要精確的轉子磁極位置。傳統的檢測方法多采用光電編碼盤等設備來測量轉子的角度以及轉速。這類設備不僅增加了成本，而且降低了可靠性，因此，需要借助無角度傳感器控制方法（以下簡稱無傳感器控制方法）。

在永磁同步電機的控制中，常見的無傳感器控制方法有：基于數學模型的開環估計、高頻信號注入法、模型參考自適應控制、狀態觀測器法、以及卡爾曼濾波器等。其中開環估計法[5]的準確性受電機參數影響非常大，而電機的參數在電機運行時總是處于動態變化之中，因此，估計效果不佳。高頻信號注入法[6]對于沒有凸極性的永磁同步電機則無能為力。至于模型參考自適應控制[7]、狀態觀測器法[8]、以及卡爾曼濾波器[9]等閉環估計方法雖然具有較好的穩定性以及魯棒性，但是算法復雜，在一些對實時性要求很高的場合，如高速電機，則難以使用。

本文研究了一種基于假定旋轉坐標的控制方法。該方法既無需角度傳感器，也無需對轉子d軸位置進行估計，就能夠實現最大轉矩電流比的控制，并且計算量不大，在實際應用中取得了很好的效果。

2 假定旋轉坐標的思想

2.1 永磁電機的數學模型

如圖1所示，d、q坐標為同步旋轉坐標，同步的含義是d軸與轉子的永磁勵磁磁場ψf保持一致，q軸超前d軸90°電角度。圖中，θr表示d軸與A軸之間的夾角，δ 表示定子電流矢量is與d軸的夾角。永磁同步電機在d、q坐標下的定子電壓方程為

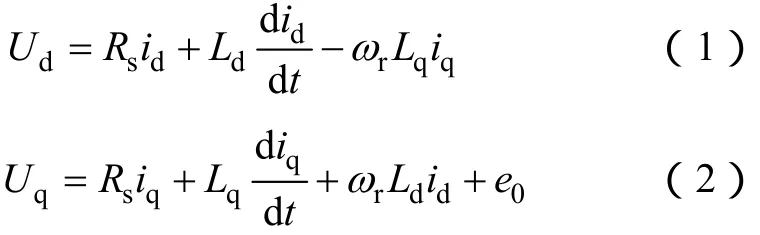
式中 Ud，Uq——電機電壓的d、q軸分量；

id，iq—— 電機電流的d、q軸分量；

Ld，Lq—— 電機電感的d、q軸分量；

Rs—— 定子電阻；

ωr——轉子電氣角速度；

e0——空載電動勢，e0=ωrψf。

電機的轉矩方程以及運動方程為

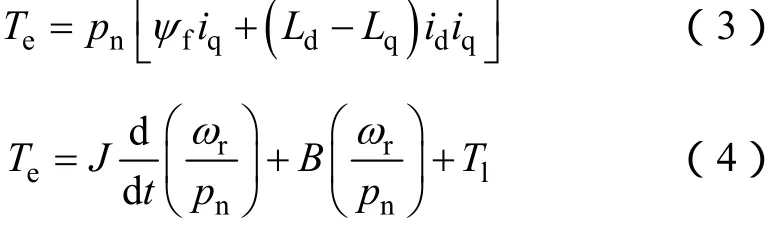
式中 Te——電磁轉矩；

pn——轉子磁極對數；

ψf——永磁體磁鏈；

J——轉子轉動慣量；

B——粘滯摩擦系數；

Tl——負載轉矩；

is，δ ——定子電流矢量及其與d軸的夾角[10]。

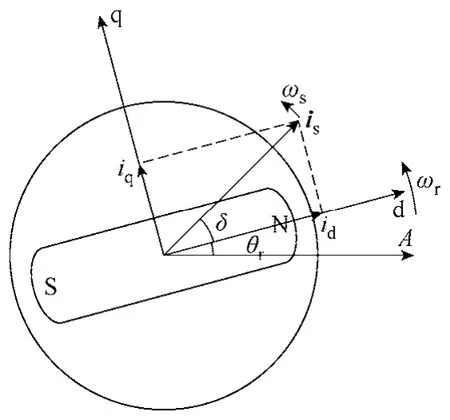
圖1 永磁同步電機同步旋轉坐標示意圖Fig.1 Diagram of synchronous rotating frame of PMSM

2.2 假定旋轉坐標系的建立

在無傳感器的控制中，由于實際轉子d軸位置θr是不能測得的，也就是不能獲得d、q坐標系中的定子電流 id、iq以及電壓 Ud、Uq，因此這個 d、q模型對于估計轉子d軸位置θr和速度ωr是沒有實用價值的。在這種情況下，選擇了一個可控的參考坐標系x、y用于無傳感器控制，其中y軸超前于x軸90°電角度。它不是同步旋轉坐標系，而是定向于已知的估計位置θr′，并且可以按照確定的控制規律自行調整的坐標系，將這個坐標稱為假定旋轉坐標，如圖2所示。圖2中ωs為假定旋轉坐標的轉速，Δθ 表示x軸與q軸的夾角。

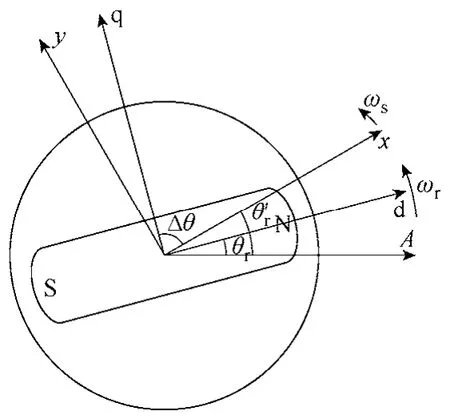
圖2 同步旋轉坐標與假定旋轉坐標關系Fig.2 Relationship between synchronous rotating frame and hypothetical reference frame

高速永磁同步電機的轉子通常采用一對極的對稱結構，即pn=1，Ld=Lq。通過d、q坐標系下的電機方程不難推導出x、y坐標系下電機的方程，由于高速永磁電機采用對稱的轉子結構，取x、y軸的電感均為L，得到電機的電壓和轉矩方程如下[10]：

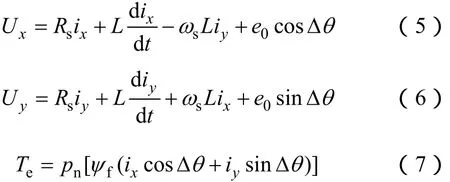
與同步旋轉坐標相類似，在假定旋轉坐標中可以通過控制Ux、Uy來得到旋轉電流矢量is。如果將ix作為電流矢量的轉矩分量，iy作為勵磁分量（文中之所以將x軸作為轉矩軸，是考慮到啟動方便的原因）。并且使得 ix=is、iy=0、Δθ=0，且由 ix產生的轉矩大小剛好克服阻力矩，那么就可以實現最大轉矩電流比的控制。

3 基于假定旋轉坐標的控制方法

3.1 現有方法及其不足

現有的基于假定旋轉坐標的控制方法大都是基于對Δθ 的估計。因為Δθ 是假定旋轉坐標的轉速ωs與轉子轉速ωr差值的積分。若已知Δθ 或者是可以反映Δθ 信息的物理量，則可以用其來調節ωs，最終使假定旋轉坐標的位置與轉子位置趨向一致[11-14]。

一種簡單的基于假定旋轉坐標的方法是從電壓方程出發對Δθ 進行估計，并將其應用到閉環控制中。具體的做法是將式（5）、式（6）變換成以下形式

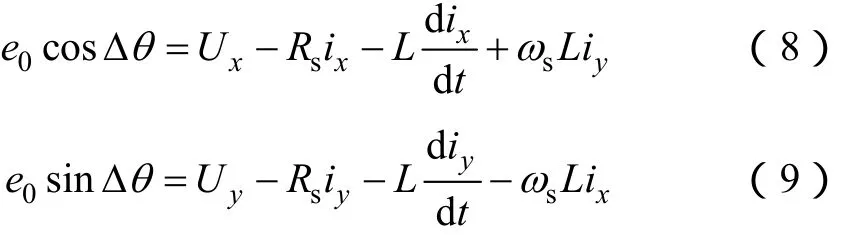
因為式（8）、式（9）是由式（1）、式（2）變換而來，沒有經過任何簡化或者近似處理，因此它們可以準確地描述電機運行狀態或動、靜態特性。可以得到

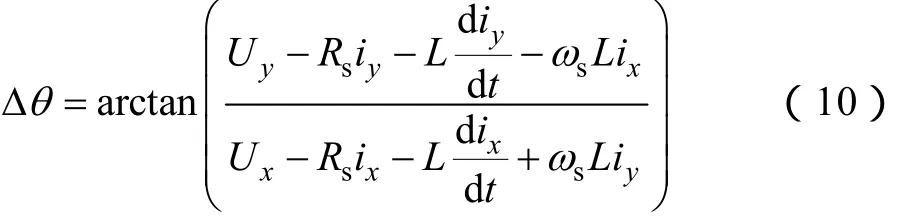
從式（10）可以看出，若忽略死區效應以及逆變器的畸變，則可以通過給定電壓值以及電流傳感器反饋回來的電流信號準確地計算出Δθ 。但是此種估計方法歸根結底是一種基于反電動勢的開環估計，其估計精度受到電機參數變化以及電流檢測精度的影響。文獻[10]指出，在穩態情況下，為保證Δθ 的估計誤差不超過5°電度角，L的偏差不能大于20%。

文獻[11]提出了一種新的估計方法，思想是根據Δθ 導致的控制電壓的偏差來調節ωs。從圖2可以看出理想情況下假定旋轉坐標的x軸與同步旋轉坐標的d軸重合，e0cosΔθ=0。則通過電流環控制 ix=0（此方法ix作為勵磁分量），Ux僅需要克服-ωsLiy。若 e0cosΔθ ≠0，則給定的 Ux還需要克服 e0cosΔθ 。于是將電流環中計算出的 Ux與理想情況下的 Ux作差，得到ΔU=e0cosΔθ ，其中包含了Δθ 的信息，對這一電壓偏差實施PI運算就得到了ωs的修正量，用修正量去調整ωs可以使位置偏差收斂為零。相對于前一種，這種方法避免了反正切函數的計算，非常容易實現，但是需要注意的是電流環中計算出的Ux與逆變器實際輸出的電壓存在差異，影響控制效果。若用電壓重構算法來實現對 Ux的計算則需要附加電壓傳感器且又復雜化了算法。

此外，現有的基于假定旋轉坐標的控制方法大都是對Δθ 或者是可以反映Δθ 信息的物理量實施 PI運算以得到ωs的修正量。而 PI參數的選擇至關重要，只有合適的PI參數才能使位置偏差最終收斂為零。而現有的文獻中并沒有具體的設計方法，PI參數的選擇很大程度上依賴于調試者的經驗。本文在研究現有方法的基礎上，提出了一種新型的基于假定旋轉坐標的控制方法。

3.2 新型假定旋轉坐標法

首先，構建假定旋轉坐標系。文中構建的假定旋轉坐標系見 2.2節。假定旋轉坐標下的電機方程如式（5）～式（7）。與一般的習慣不同，文中將x軸定義為轉矩軸，y軸定義為勵磁軸。于是需要達到的控制目標是iy=0、Δθ=0，且由ix產生的轉矩大小剛好克服阻力矩。

從圖2可以看出，當通過假定旋轉坐標來控制永磁電機時，Δθ＞0表示轉矩軸 x軸落后于轉子 q軸，這時希望減小轉子轉速ωr，以使x軸趕超q軸。Δθ ＜0則x軸超前于轉子q軸，希望增大ωr。而當Δθ=0時，ix全部作用在轉子q軸，且感應電動勢在y軸的分量e0sinΔθ 也為零。此時，只要使得iy=0，對于轉子結構對稱（Ld=Lq）的永磁電機，就實現了最大轉矩電流比控制。因此可以根據位置偏差信息Δθ 來調節轉子的轉速ωr。

Δθ 無法直接測得，如3.1節中所述，若開環估計Δθ ，估計的準確性受電機參數影響很大。若使用模型參考自適應方法或是狀態觀測器來估計Δθ ，算法將非常復雜。因此，本文選擇用包含Δθ 信息的物理量來代替Δθ 對轉子的轉速ωr進行調節。

令Uy=ωsLix，則式（6）可以改寫成如下形式

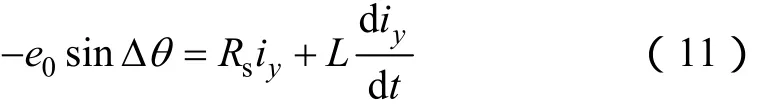
在理想情況下Δθ=0，e0sin Δθ=0，則 iy為 0。若Δθ ≠0，則必然能夠測出一個 iy，且 iy的值決定于轉子反電動勢 e0、位置偏差Δθ 、定子電阻 Rs以及電感L。在這四個量當中 Rs、L是定值，e0=ωrψf，對于數字化的控制系統，每一個采樣周期內，由于機械時間常數遠大于電氣時間常數，可以認為ωr是不變的，而ψf也是常量。因此，通過式（11）可以看出在Δθ ∈[-π/2，π/2]時，iy是Δθ 的單調減函數。而iy是非常易測得的，因此，可以用iy代替Δθ 來調節轉子的轉速ωr。iy＜0時Δθ ＞0，轉矩軸 x軸落后于轉子q軸，這時減小轉子轉速ωr。iy＞0時Δθ ＜0則 x軸超前于轉子 q軸，增大ωr。iy=0時Δθ=0，ix全部作用在轉子q軸，假定旋轉坐標與轉子實際位置重合，實現了最大轉矩電流比控制。

3.3 控制器的設計及仿真

如 3.1節所述，現有的基于假定旋轉坐標的控制方法大都沒有從理論上對控制器的參數選擇給出具體的方案。本文以系統的穩定裕度為依據給出了控制器的設計方法。

首先，分析在平衡位置（Δθ=0）附近控制系統的穩定性。將sinΔθ 在Δθ=0處作泰勒級數展開，取一次項近似，得到 sin Δθ ≈Δθ （在Δθ=0 附近），將e0看做常量，則可以得到Δθ 與iy之間傳遞函數為

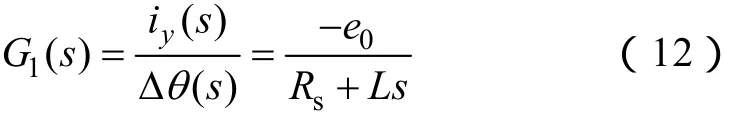
根據轉矩方程式（7）可知，永磁電機提供的轉矩與 ix、iy以及Δθ 三個變量有關。但是在平衡位置附近時Δθ ≈0，可以忽略 iysinΔθ 對電磁轉矩的影響，將式（7）簡化為 Te=pnψfix。由運動方程式（4）可以得到電磁轉矩與轉速之間的傳遞函數如下：

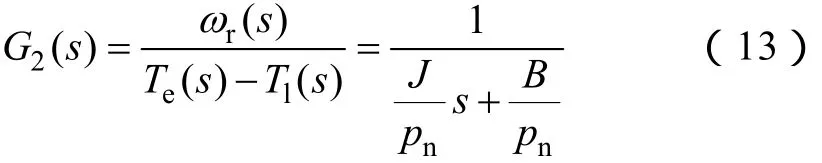
若設負載轉矩 Tl為0、不考慮粘滯摩擦系數且轉子為一對極結構，則可以得到永磁電機以Ux為輸入iy為輸出的結構圖如圖3所示。

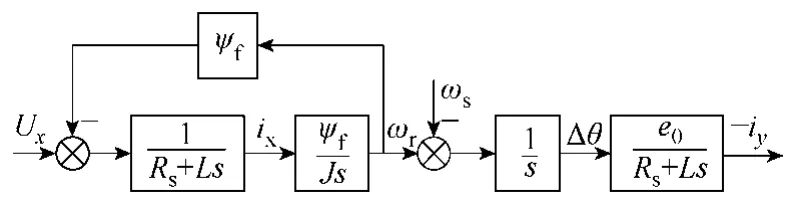
圖3 永磁同步電機結構圖Fig.3 Structural drawing of PMSM

因為在建立數學模型的時候將e0看成常數，因此圖3中系統的開環傳遞函數不僅與電機參數有關而且與當前轉速相關。代入下表高速永磁同步電機的參數，繪制出圖3系統在轉速為27 000r/min時的開環對數頻率特性曲線如圖4所示。

表 高速永磁電機參數Tab.Parameter of high speed PMSM

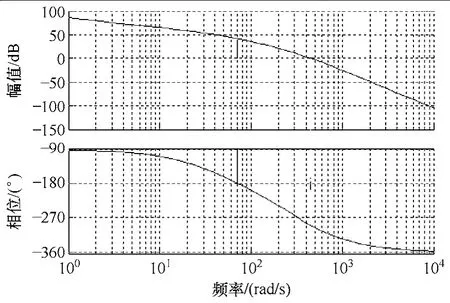
圖4 高速永磁同步電機開環頻率特性曲線Fig.4 Open-loop frequency characteristic of high speed PMSM

從圖 4中可以看出系統的幅值裕度 h(dB)=-41.2dB，相角裕度γ=-109°。可見，以圖3所示的傳遞函數為前向通路的單位反饋系統是不穩定的，必須對其進行校正。

對于高速永磁同步電機來說，基本不存在轉速的突變，不需要系統有很高的動態響應。此外，中大功率的高速永磁電機通常將定子的電阻和電感都設計得很小，這樣的系統對噪聲比較敏感。因此可以利用滯后網絡或PI控制器對系統進行串聯校正。

文中設計了串聯滯后網絡對系統進行校正，將校正后系統的相角裕度設定在 45°左右得到滯后網絡的傳遞函數為

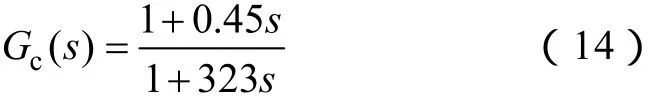
得到校正后系統的開環對數頻率特性曲線如圖5所示，從圖中可以得到以校正系統的幅值裕度h′(dB)=15.3dB，相角裕度γ ′=43.9°，符合要求。此時閉環系統的單位階躍響應如圖6所示。

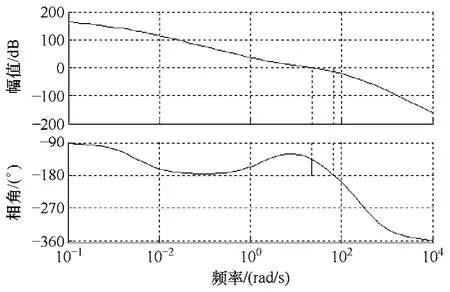
圖5 校正后高速永磁同步電機開環頻率特性曲線Fig.5 Open-loop frequency characteristic of high speed PMSM after correcting

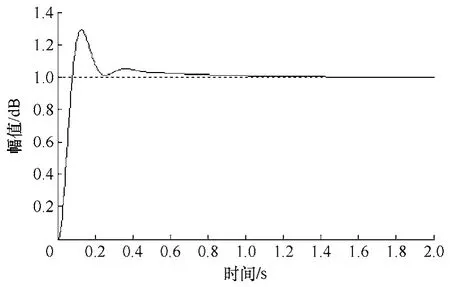
圖6 高速永磁同步電機閉環控制系統的單位階躍響應Fig.6 Unit step response of closed-loop control system for high speed PMSM

為驗證控制方法的正確性，在Matlab/Simulink環境下建立了基于假定旋轉坐標的無傳感器控制系統的仿真模型，如圖7所示。其中串聯滯后環節如式（14）所示，ωsLix是為了抵消式（6）中由定子電流產生的旋轉電勢。仿真中永磁同步電機參數見上表，仿真是在27 000r/min的仿真轉速下進行的。

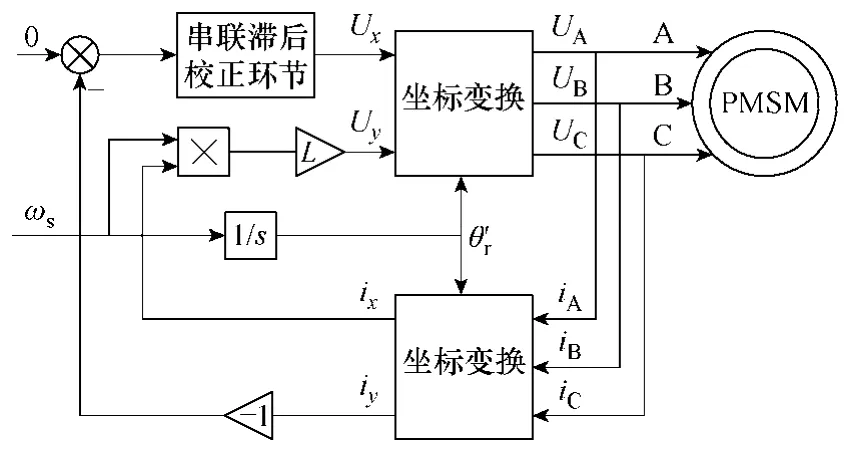
圖7 基于假定旋轉坐標的無傳感器控制系統框圖Fig.7 Diagram of sensorless control system based on hypothetical reference frame

仿真中，先用開環控制將電機帶到27 000r/min的轉速，在仿真時間10s時切換到文中設計的閉環算法，仿真波形如圖8所示。圖8a為轉子轉速的仿真波形，可以看出，在算法切換的瞬間，轉子轉速有一個振蕩的過程，經過一段時間的調整后收斂于同步轉速。算法的切換不會造成系統的發散，適當地調節控制器參數可以更好地抑制此振蕩。圖 8b為運行中x軸與轉子q軸的夾角，即Δθ 的角度。從圖中可以看出在系統穩定以后Δθ 的角度趨近于0，此時x軸與轉子q軸重合，即ix全部作用在轉子q軸上。兩個坐標系下的電流分量的變化如圖8c、8d所示，可以看出，在切換瞬間id遠大于零。根據調節規律，控制器減小 ix，則 id減小，iy增大，最終使id收斂于零，與3.2節中的分析完全相同。為進一步驗證，從圖 8c中讀出 27 000r/min時，x軸電流 ix穩定在 133.16A，此時電機提供的電磁轉矩Te=pnψfix近似為15.98N·m。此時加在電機上的負載轉矩 Tl設置為轉速平方的 2×10-6倍，近似等于15.98N·m，兩者非常接近，很好地驗證了結論。

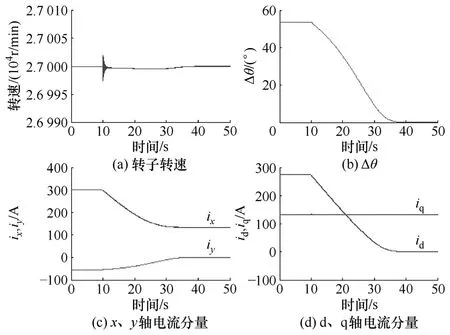
圖8 無傳感器控制系統仿真波形Fig.8 Simulation waveforms for the sensorless control system

圖9給出了在27 000r/min的高轉速下，負載轉矩由15.98N·m突變至12N·m時電機的轉速響應以及提供的電磁轉矩的仿真波形。如圖9所示，在仿真時間 50s時將負載轉矩由 15.98N·m改為12N·m，可以看出，電磁轉矩經過短時間的調整很好地跟蹤了負載轉矩，在負載突變的瞬間，轉子轉速以及電磁轉矩出現了一段時間的振蕩，可根據實際情況修改控制器參數來給予調節。

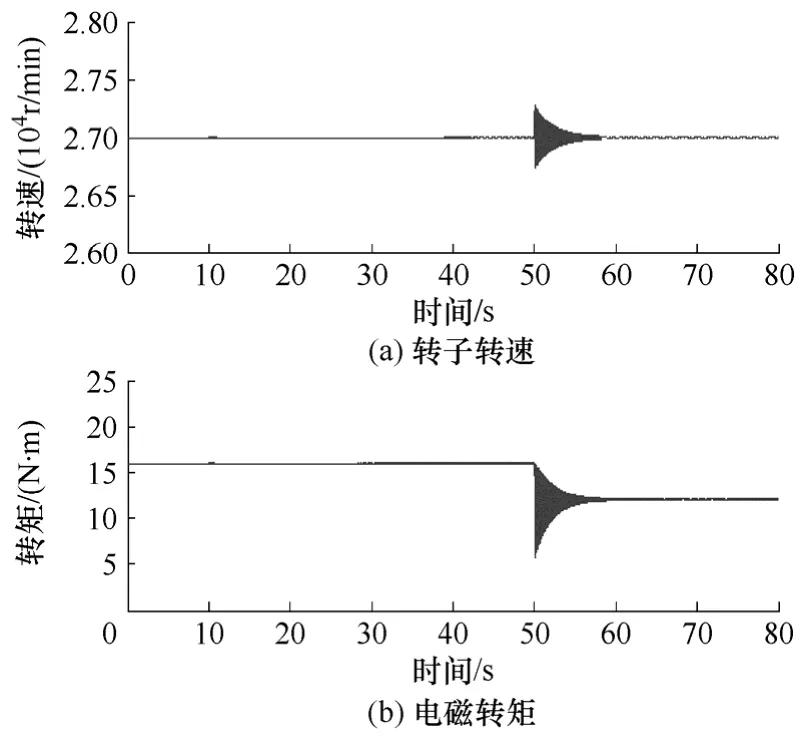
圖9 負載突變時電磁轉矩以及轉速的響應波形Fig.9 Response of electromagnetic torque and speed when load changing

仿真過程中，可以適當增加開環增益來提高系統的收斂速度。

4 實驗研究

為驗證結論，文中以美國Ti公司的高性能數字信號處理器 TMS320F28335為核心設計了硬件電路。主電路結構如圖10所示，其中逆變部分采用的是三相全橋式拓撲結構，功率器件選用的是德國Semikron公司的SEMIX604GB12T4S。控制器采集永磁同步電機的三相電流及逆變器的母線電壓通過文中設計的控制算法對永磁同步電機進行控制。

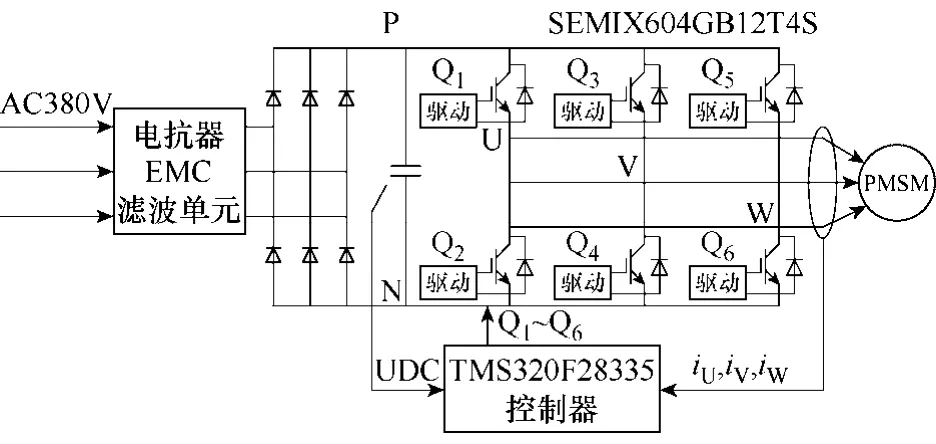
圖10 無傳感器控制系統的電路結構Fig.10 Electrocircuit of sensorless control system

文中以實際的磁懸浮高速離心式鼓風機（見圖11）為對象進行了驗證實驗。驅動鼓風機葉輪所用永磁同步電機規格參數為：額定功率 75kW；額定電壓 380V；相電阻 0.15Ω；相電感 0.35mH；永磁體磁鏈0.12Wb；轉動慣量0.003kg·m2；磁極對數為 1。以下實驗波形均以美國立肯（LeCroy）公司的 WaveRunner 64Xi—A型示波器保存波形數據后在Matlab中繪制。

圖11 磁懸浮高速離心式鼓風機Fig.11 High speed centrifugal blower supported by active magnet bearing

文中首先通過開環控制將電機穩定運行于27 000r/min的轉速下，此時定子相電流的波形如圖12所示，從圖中可以讀出相電流的峰峰值約為340A。在負載不變的情況下，切換到文中提出的基于假定旋轉坐標的控制方法，穩定后定子相電流的波形如圖13所示，其峰峰值約為300A。可見在文中的方法控制下電機在相同負載下的相電流相對于開環控制時大大減小。

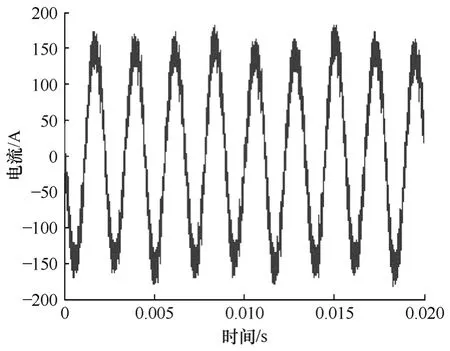
圖12 開環控制下27 000r/min時定子相電流波形Fig.12 Waveform of phase current using open loop control method under the speed of 27 000r/min

圖13 文中方法控制下27 000r/min時定子相電流波形Fig.13 Waveform of phase current using the sensorless control strategy under the speed of 27 000r/min

為進一步驗證該方法的控制效果，當電機穩定運行于27 000r/min時，將ix、iy通過D-A芯片實時輸出，波形如圖14所示。可見，x軸電流波形平穩，即轉矩穩定，y軸電流幾近為0，與控制的初衷相符。因此，可以得出結論，文中提出的基于假定旋轉坐標的控制方法很好地達到了最大轉矩電流比的控制效果。

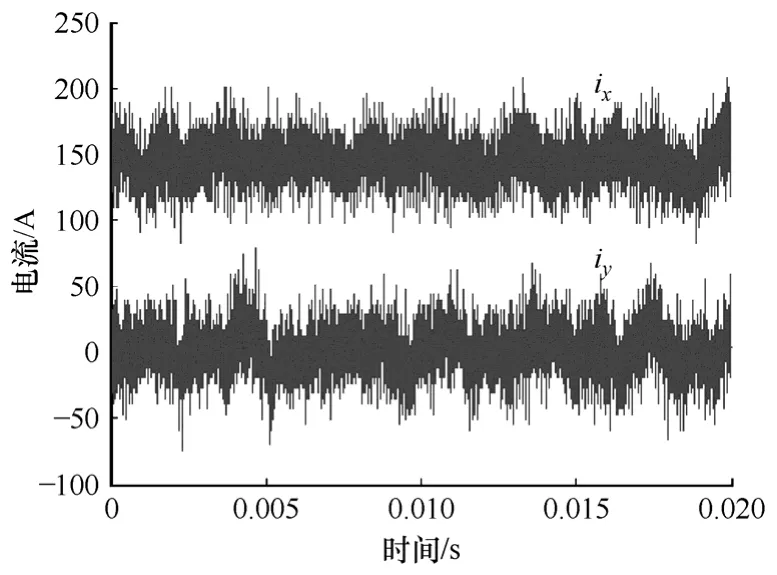
圖14 27 000r/min時ix、iy的電流波形Fig.14 Waveform of ix、iy under the speed of 27 000r/min

5 結論

文中提出了一種新型的基于假定旋轉坐標的永磁同步電機無傳感器控制方法，分析了該方法的工作原理，并通過仿真與試驗對其可行性進行了驗證。仿真以及試驗結果均證明，文中研究的無傳感器控制方法能夠實現永磁同步電機的最大電流轉矩比控制，且具有良好的動態性能。

[1]Hennau J.Active magnetic bearings for use in compressors and other turbo machinery[J].Turbomachinery International, 1989, 30(1): 15-20.

[2]Mizuno T, Bleuler H, Tanaka H.Industrial application of position sensorless active magnetic bearings[J].Electrical Engineering in Japan, 1996,117(5): 124-133.

[3]王繼強, 王鳳翔, 孔曉光.高速永磁發電機的設計與電磁性能分析[J].中國電機工程學報, 2008,28(20): 105-110.Wang J Q, Wang F X, Kong X G.Design and analysis of electromagnetic properties for high speed PM generator[J].Proceedings of the CSEE, 2008, 28(20):105-110.

[4]王繼強, 王鳳翔, 鮑文博, 等.高速永磁電機轉子設計與強度分析[J].中國電機工程學報, 2005,25(15): 140-145.Wang J Q, Wang F X, Bao W B, etal.Rotor design and strength analysis of high speed permanent magnet machine[J].Proceedings of the CSEE, 2005, 25(15):140-145.

[5]Wu R, Slemon G R.A permanent magnet motor drive without a shaft sensor[J].IEEE Trans on Industry Applications, 1991, 27(5): 1005-1011.

[6]Schroedl M, Weinmeier P.Sensorless control of reluctance machines at arbitrary operating conditions including standstill[J].IEEE Trans on Power Electronics, 1994, 9(2): 225-231.

[7]Matsui N.Sensorless PM brushless DC motor drives[J].IEEE Trans on Industrial Electronics, 1996,43(2): 300-308.

[8]Bolognani S, Oboe R, Zigliotto M.Sensorless full-digital PMSM drive with EKF estimation of speed and rotor position[J].IEEE Trans on Industrial Electronics, 1999, 46(1): 184-191.

[9]Dhaouadi R, Mohan N, Norum L.Design and implementation of an extended kalman filter for the state estimation of a permanent magnet synchronous motor[J].IEEE Trans on Power Electronics, 1991,6(3): 491-497.

[10]王成元, 夏加寬, 孫宜標.現代電機控制技術[M].北京: 機械工業出版社, 2008.

[11]Nobuyuki Matsui, Masakane Shigyo.Brushless DC motor control without position and speed sensors[J].IEEE Trans on Industry Applications, 1992, 28(1):120-127.

[12]袁澤劍, 楊耕, 鐘彥儒.永磁同步電機無位置傳感器矢量控制系統的研究[J].電氣傳動自動化, 2000,22(4): 21-23.Yuan Z J, Yang G, Zhong Y R.Research on permanent magnet synchronous motor vector control without position sensors[J].Electrical Drive Automation, 2000, 22(4): 21-23.

[13]葉軍軍.基于模糊控制的永磁同步電機矢量控制系統的研究[D].武漢: 武漢理工大學, 2006.

[14]楊波.基于高頻注入法的電梯曳引機轉子位置估計的研究[D].沈陽: 沈陽工業大學, 2010.