基于SFDICT磁鏈位置積分器的直驅永磁風力發電機無傳感器控制

唐 芬 金新民 周 嘯 趙 新 童亦斌

（北京交通大學電氣工程學院 北京 100044）

1 引言

直驅永磁風力發電機組因其在效率、可靠性、并網控制靈活等方面的優勢，成為變速恒頻風力發電領域的重要發展方向[1-4]。

在直驅風力發電系統中，永磁風力發電機常與風力機直接相連接，其機械結構往往使編碼器無法安裝。為此，無傳感器技術成為了直驅永磁風力發電技術的研究熱點之一。文獻[5]采用基于定子電流的狀態觀測器模型，針對面裝式兆瓦級直驅風電機組的特點，具有工程實現簡單，魯棒性較好，但是此方法用于凸極永磁同步電機，算法仍比較復雜。文獻[6]基于鎖相環原理，構建位置觀測器具有原理簡單、設計方便、工程容易實現，但是在動態過程中，如轉速變化和轉矩突變時性能較差。文獻[7]提出基于帶坐標變換的飽和反饋雙積分器（Saturation Feedback Double Integrator Based on Coordinate Transform，SFDICT）的無傳感器控制，應用于兆瓦級直驅永磁風力發電機中具有較好的動、穩態性能。但由于電機非理想因素和控制原因，電機定子反電動勢存在直流、5次、7次等諧波含量，若仍采用其限幅值選取方法存在以下兩個問題：由于定子反電動勢諧波存在，估算磁鏈處于時而限幅時而未被限幅狀態，導致定子電流諧波增加；限幅值稍有偏差很容易進入實際磁鏈值大于限幅值的工況，導致定子電流存在較大的直流分量和2次諧波，影響整個變流器的控制。

考慮到兆瓦級直驅永磁發電機具有轉動慣量大、轉速變化平緩，在切入風速點定子電壓仍有較高頻率和幅值的特點。本文仍采用基于SFDICT磁鏈位置積分器的無傳感器控制。通過分析 SFDICT在不同諧波含量、不同限幅值下的工作特性，提出了SFDICT在不同限幅值下的誤差分析公式。并在此基礎上提出小限幅值加角度補償的磁鏈估算方法：設置SFDICT限幅值低于實際基波磁鏈值，使穩態一直處于限幅狀態，再用誤差分析公式進行角度補償。最后應用于25kW和2MW永磁風力發電機進行了實驗驗證。

2 基于磁鏈位置積分器的無傳感器控制

將d軸定向在轉子磁鏈方向上，其與兩相靜止坐標系αβ間的夾角為θe，利用坐標變換理論，可得永磁同步電機在同步旋轉坐標系d、q軸下的電壓方程、磁鏈方程和轉矩方程分別如式（1）～式（3）所示，d、q軸等效電路分別如圖1所示[8]。

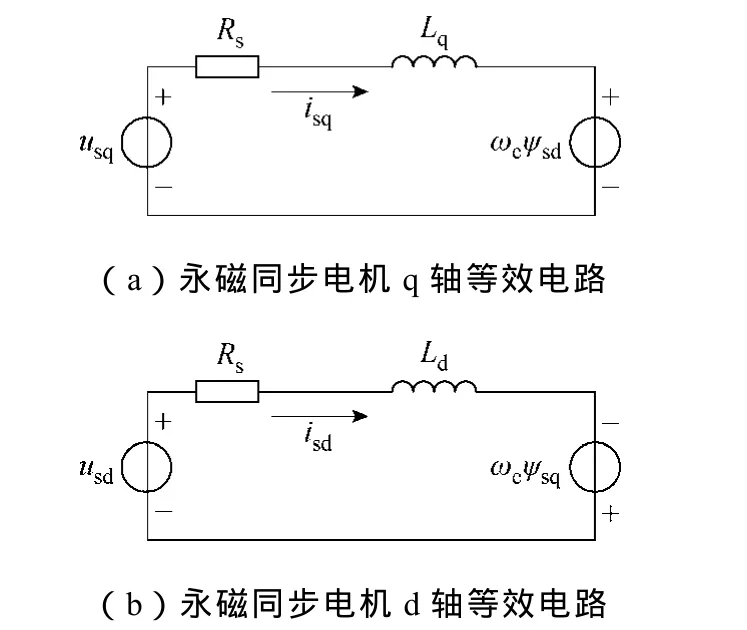
圖1 永磁同步電機dq軸等效電路Fig.1 q axis and d axis equivalent circuits of PMSG

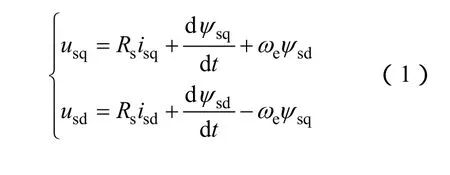
磁鏈方程為

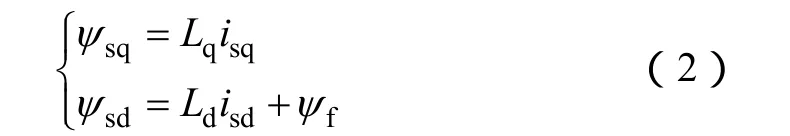
轉矩方程為

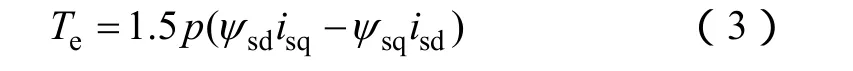
式中 usd，usq—定子電壓d、q軸分量；

isd，isq—定子電流d、q軸分量，以電動方向為正；

Ld，Lq—d、q軸同步電感；

Rs—定子電阻；

ωe—電角速度；

ψf—轉子磁鏈；

ψsd，ψsq—定子磁鏈d、q軸分量；

Te—電磁轉矩；

p—極對數。

永磁風力發電機各控制策略的不同點在于電機控制目標的不同，最終體現在永磁同步電機指令的變化上，對本文重點討論的無傳感器控制影響較小，為簡化分析，本文以零 d軸電流控制（ZDAC）為例進行闡述，其控制目標是將永磁同步電機d軸電流控制為零，即isd=0，則轉矩方程變為

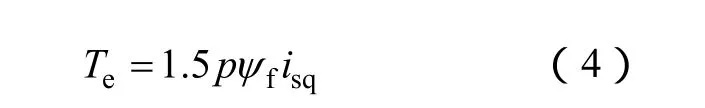
認為ψf恒定，則電磁轉矩與isq成正比，這就是ZDAC的優點之一，即電磁轉矩與定子電流呈線性關系，其性能類似于直流電機，控制簡單，無去磁作用，因此，得到了廣泛應用。

忽略定子電阻，可得采用ZDAC永磁同步電機處于發電工況時的矢量圖如圖2所示，其中，Is為定子電流矢量；Us為定子電壓矢量；ψf為轉子磁鏈矢量，與α 軸夾角為θe；ψs為定子磁鏈矢量，與α軸夾角為θs；δ為功角。可見，ψf和ψs存在如式（5）關系，可由定子磁鏈位置得到轉子磁鏈位置。

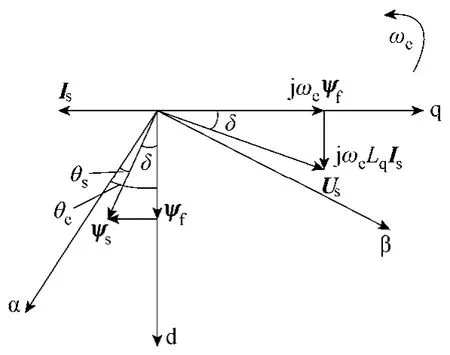
圖2 采用ZDAC永磁同步電機處于發電工況時矢量圖Fig.2 Vector diagram of PMSG under generating condition with ZDAC control

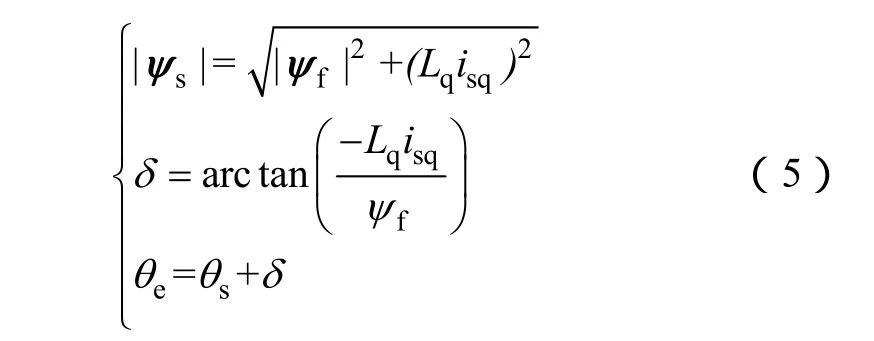
Us、Is、ψs與定子反電動勢矢量 Es關系如式（6）所示，分量表示時如式（7）所示，其中usα、usβ分別為定子電壓α、β軸分量；isα、isβ分別為定子電流α、β軸分量；ψsα、ψsβ分別為定子磁鏈α、β軸分量；Esα、Esβ分別為定子反電動勢α、β軸分量。

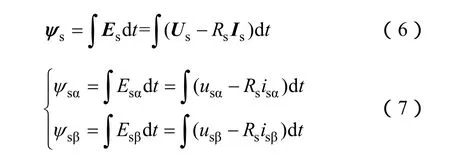
定子磁鏈可通過對反電動勢信號的積分得到，該方法只需用到電機的定子參數，而不需要電機的轉速信息，計算簡單，因此得到了廣泛的應用。但積分器設計優劣直接影響到磁鏈位置觀測的準確性。本文將從定子反電動勢中得到轉子磁鏈位置的積分器稱為磁鏈位置積分器。

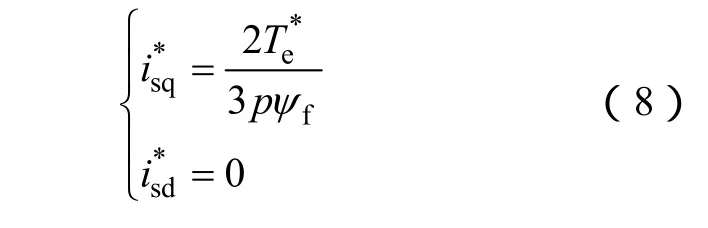
要使實際電流跟蹤指令電流，加入反饋控制，采用PI調節器，則基于磁鏈位置積分器的無傳感器控制框圖如圖3所示。

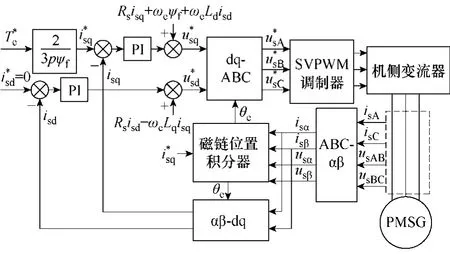
圖3 基于磁鏈位置積分器的永磁同步電機無傳感器控制框圖Fig.3 Block diagram of sensorless control based on rotor flux linkage position integrator

3 帶坐標變換的飽和反饋雙積分器

當輸入信號存在測量誤差、直流偏移等時，純積分器存在積分飽和和初始值等問題。而用一個截止頻率較低的低通濾波積分器代替純積分器，雖然解決了上述問題，但低通濾波積分器存在幅值和相位誤差。針對該問題，本文采用帶坐標變換的飽和反饋雙積分器（SFDICT）[9-11]，其控制框圖和傳遞函數分別如圖4和式（9）、式（10）所示。其中ψss為SFDICT估算定子磁鏈，其α、β軸分量分別為ψssα和ψssβ，ψz為限幅值，ψsz為估算磁鏈經過限幅模塊后輸出，其α、β軸分量分別為ψszα和ψszβ。該積分器由兩部分組成：前饋部分ψs1=Es/(s+ωc)，其α、β軸分量分別為ψs1α和ψs1β，為典型低通濾波積分器；反饋部分ψs2=ωcψsz/(s+ωc)，其α、β軸分量分別為ψs2α和ψs2β。其具有以下特點：

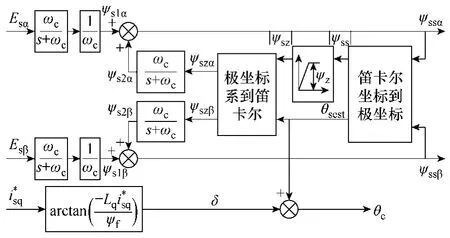
圖4 帶坐標變換的飽和反饋雙積分器框圖Fig.4 Block diagram of SFDICT

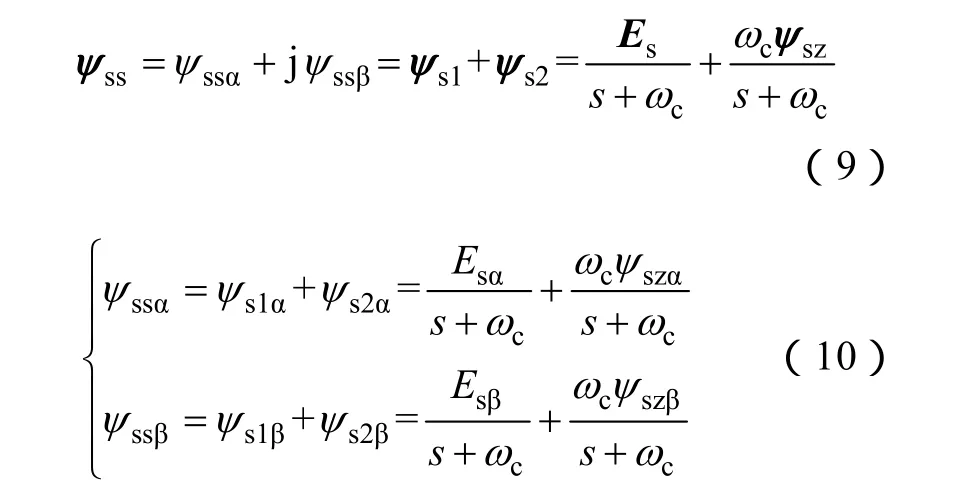
當ψz=0時，為低通濾波積分器，存在幅值和相位誤差，在此僅討論ψz＞0的情況。

當ψz＞|ψss|時，磁鏈未被限幅，ψsz=ψss，則|ψsz|=|ψss|＜ψz。同時，由式（9）可推導ψss=Es/s，相當于以上一次被限幅時系統各量為初始狀態的純積分器，若整個過程一直未被限幅，則輸出為純積分器的輸出。

當ψz≤|ψss|時，磁鏈被限幅，則ψsz=ψzψss/|ψss|。可見，ψsz與估算值ψss瞬時同相，|ψsz|=ψz≤|ψss|。

可見，由于限幅模塊的存在，有|ψsz|≤|ψss|和|ψsz|≤ψz成立。

由于采用磁鏈位置積分器的目的是為了得到轉子磁鏈位置和坐標變換角度，故希望得到的是轉子磁鏈的基波位置，因此將檢測和實際存在的其他頻率分量作為誤差處理。假設理想的定子反電動勢、定子磁鏈僅含有基波分量且分別為、。考慮到檢測定子反電動勢時難免存在測量誤差和直流偏移，并考慮到變流器驅動永磁同步電機特點，將直流偏移以直流分量Esdc表示，低次諧波以 5次諧波為例以 Es5表示，高次諧波以開關頻率諧波為例以Esfs表示。其中下標e、dc、5、fs分別表示基波分量、直流分量、5次諧波分量、開關頻率分量。根據疊加定理，由式（9）可得各矢量基波分量間存在

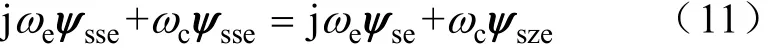
若ψsze與ψsse同相且|ψsze|≤|ψsse|，則矢量基波分量間關系如圖5所示，可見，ψm≥|ψsse|，即估算磁鏈基波幅值小于等于真實磁鏈，且真實磁鏈位置滯后或者等于估算磁鏈基波。當且僅當|ψsze|=|ψsse|，無基波幅值和角度誤差。

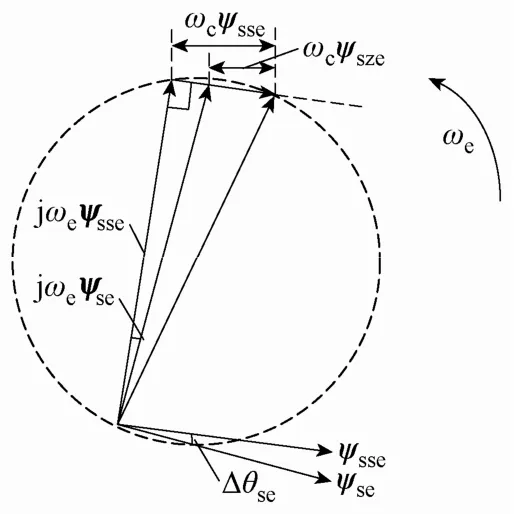
圖5 SFDICT矢量基波分量間關系Fig.5 Relationship fundamental vectors of SFDICT

令 kL=ψz/ψm，若進一步有ψsze=ψzψsse/|ψsse|成立，則估算磁鏈基波幅值與實際磁鏈幅值比值 ksse和基波位置估算誤差Δθse（ψsse與ψse間夾角）為

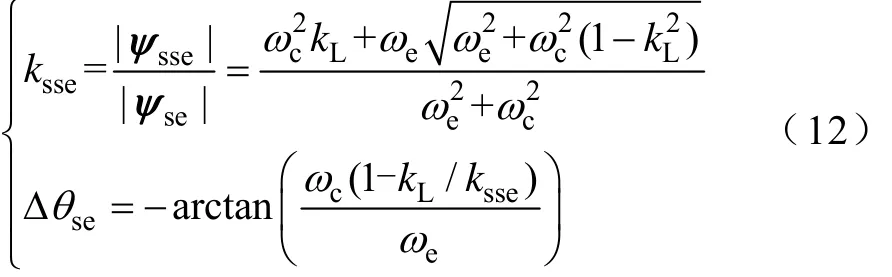
由ksse對kL求導可得，在0≤kL≤1區間內，ksse單調遞增且ωe/≤ksse≤1，Δθse隨 kL單調遞增且-arctan(ωc/ωe)≤Δθse≤0。

3.1 不同限幅值下的SFDICT誤差特點

僅考慮Ese時，ψs1由基波分量和初始值引起的暫態直流衰減量組成，穩態時僅含有基波分量，則穩態時ψss和ψs2僅能含有基波差值，即使含有其他頻率分量，也應等量。

3.1.1 穩態一直處于被限幅狀態

若穩態輸出一直處于被限幅狀態，則|ψsz|=ψz，根據周期函數特點，ψsz可寫成式（13），其中 k為整數，Ψszk為k次諧波幅值，下標k表示k次諧波。

根據式（14）幅值脈動項特點以及式（15）穩態關系，要使|ψsz|恒定，則ψss和ψsz只能含有基波分量，即ψsse=ψss，ψsze=ψsz。又因ψsze=ψzψsse/|ψsse|，且|ψsze|=ψz≤|ψsse|，故矢量基波分量間關系滿足圖 5和式（12）。由于穩態時均只含有基波分量，因此kss=|ψss|/|ψs|=ksse，位置估算誤差（ψss與ψs間夾角）Δθs=Δθse。

3.1.2 穩態一直處于未被限幅狀態

若穩態一直未被限幅，則ψsz=ψss。由穩態時ψss和ψs2僅能含有基波差值。則應用疊加定理，對于k次諧波，k≠1時有

可見，穩態未被限幅時，若含有其他頻率分量，則只能含有直流分量。

由ψz＞|ψss|，ψsz=ψss可得ψsse=ψsze。滿足ψsze、ψsse同相且|ψsze|≤|ψsse|，圖 5 矢量基波分量間穩態關系仍成立，可得ψsse=ψse，即估算磁鏈基波等于實際磁鏈，則ψz＞|ψse|=ψm。由穩態時ψss若含有其他頻率分量，則只能為直流分量，即穩態時ψss由基波分量和直流分量組成。若暫態過程一直未被限幅，則輸出為純積分器輸出。由純積分器分析可知，輸出為ψse與直流分量-(ψmcosφ+jψmsinφ)疊加，|ψss|在0～2ψm間變化。若ψz＞2ψm，暫態過程將不會被限幅，輸出將為純積分器輸出。若ψm＜ψz≤2ψm，則在暫態過程中有被限幅，而由于穩態處于未限幅狀態，磁鏈幅值無突變，則系統進入穩態前最后一次被限幅時|ψss|=ψz，之后ψss將為ψse與直流分量ψz-ψm疊加。則kss將在（2-kL）～kL間變化，幅值誤差比值Δkss在±(kL-1)間變化，Δθs在±arcsin（kL-1）間變化，變化頻率均為基波頻率fe。

綜上所述，僅考慮Ese時，不同kL取值下SFDICT估算磁鏈誤差公式與特點如表1所示。可見，當且僅當 kL=1即限幅值設為實際磁鏈幅值時，SFDICT估算磁鏈無穩態幅值和位置誤差。當 kL＜1，穩態幅值和位置誤差為恒定值，其值由式（12）決定，且ωc/ωe越小，kL越大，穩態幅值和位置誤差越小，但ωc過小，動態衰減過程較慢。當kL＞1時，由于Δθs以頻率 fe脈動，將其作為坐標變換定向角時，將會導致系統含有直流分量和2次諧波。

3.2 不同諧波含量下的SFDICT誤差特點

當定子反電動勢含有直流誤差Esdc時，Ψs1由基波分量、初始值引起的暫態直流衰減量、直流誤差導致的隨時間逐漸趨近于穩定值Esdc/ωc組成，穩態時僅含有基波分量和直流分量 Esdc/ωc。則穩態時ψss、ψs2僅能含有基波和直流分量差值，即使含有其他頻率分量，也應等量。若穩態時，輸出磁鏈一直處于未被限幅狀態，即|ψss|＜ψz，則 SFDICT相當于純積分器，輸出量含有由直流誤差導致的隨時間不斷累積的分量，最終將導致輸出磁鏈被限幅，因此，穩態時，輸出磁鏈不可能一直處于未被限幅狀態。應用疊加定理，穩態時系統中各量滿足

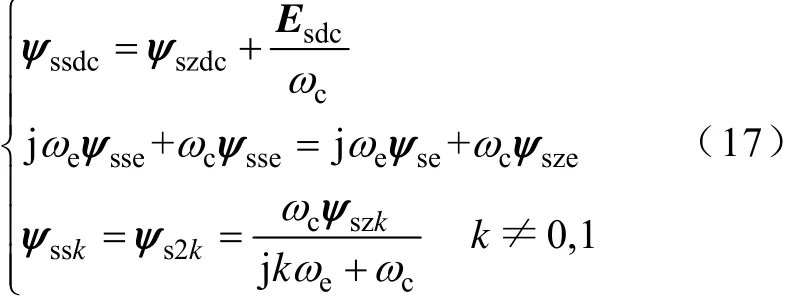
一般而言，|Esdc/ωc|?ψm，在設置ωc和ψz時，常使ψz?|Esdc/ωc|，否則ψs2≈0，與低通濾波積分器類似，仍會存在較大幅值和位置估算誤差。因此，在此僅討論ψz?|Esdc/ωc|的情況。

3.2.1 穩態一直處于被限幅狀態

若穩態一直處于被限幅狀態，則ψsz=ψzψss/|ψss|，|ψsz|=ψz≤|ψss|。由式（14）幅值特點，要使|ψsz|恒定，則ψsz只能主要含有一種頻率成分，由式（17）中ψsz、ψss間關系，ψsz將主要含有基波分量。而 Esdc/ωc雖然幅值小，但還是會導致ψsz和ψss含有一定的直流分量，這個含量和基波相比是可忽略的。由于|ψsz|恒定，因此ψsz將含有約等于直流分量幅值的2次諧波分量，來抵消基波與直流量導致的基波頻率的幅值脈動，而2次諧波與直流量將會導致幅度更小的2次脈動，ψsz可含有更小量的3次等諧波來抵消，高次諧波含量將越來越小，基本可忽略。故在此僅討論基波、直流量、2次諧波量，且直流量和2次諧波量滿足式（18），相對于基波分量，直流量和2次諧波含量可忽略。

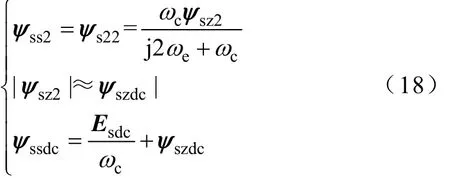
由于ψsz、ψss均主要含有基波分量，則ψsse≈ψss，ψsze≈ψsz，且ψsze≈ψzψsse/|ψsse|，|ψsze|≈ψz≤|ψss|≈|ψsse|。故矢量基波分量間關系基本滿足圖 5和式（12），可知|ψse|≥|ψsse|，即估算磁鏈基波幅值小于等于真實磁鏈，且真實磁鏈角度滯后或等于估算磁鏈基波角度。|ψss|將在稍偏離|ψsse|附近脈動，當ψz很接近ψm時，ψsse很接近于ψse，考慮到|ψss|脈動，輸出磁鏈可能有局部區域未被限幅，從而進入穩態時而限幅時而未被限幅的混合狀態。

表1 不同kL取值下SFDICT估算誤差公式與特點Tab.1 Error formula and features using SFDICT under different kL

當定子反電動勢含有 Es5時，與 Esdc類似，ψsz將主要含有基波分量，且同樣基本滿足圖 5和式（12）。另外，ψsz還將含有3次和5次諧波，其含量很小相對于基波分量可忽略。由于ψsz經低通濾波器后得到ψs2，則ψs2中3次和5次諧波基本可忽略，ψss5≈Es5/(j5ωe+ωc)。

當定子反電動勢含有Esfs時，與Esdc類似，ψsz將主要含有基波分量，并基本滿足圖5和式（12）。另外，ψsz還將含有開關頻率分量和頻率為2fe-fs的分量，兩者幅值基本相等，且其含量很小，相對于基波分量可忽略。由于ψsz經低通濾波器后得到ψs2，則ψssfs≈Esfs/(jωfs+ωc)。

3.2.2 穩態處于時而限幅時而未被限幅的混合狀態

當考慮 Esdc時，由于|ψss|脈動，則當ψz很接近ψm時，ψsse≈ψse，輸出磁鏈可能有局部區域未被限幅，由于未限幅區域很小，其幅值和位置誤差特點仍與穩態一直被限幅時類似。但隨著ψz增加，將有越來越多區域處于未被限幅狀態，其極限情況為一直處于未被限幅狀態（雖然輸入含有直流分量時，不可能達到這種狀態，但能夠無限接近），此時ψss≈ψsz，則ψsse≈ψsze，由圖 5存在ψsse≈ψse。由穩態關系，ψss和ψsz將主要含有基波和直流分量，其他諧波含量均可忽略，且|Esdc/ωc|相對于ψss和ψsz中直流分量也可忽略。由于仍有極小部分限幅，則直流分量將約為ψz-ψm，|ψss|在(2ψm-ψz)～ψz之間脈動，Δkss在±（kL-1）間變化，Δθs在±arcsin(kL-1)間脈動，脈動頻率均為 fe。在此階段，輸出磁鏈基波含量基本不變，約為實際磁鏈，但輸出磁鏈中直流分量隨ψz增大而顯著增加。同理對于5次諧波和開關頻率分量。也具有相同結論。

由于低通濾波積分器特點，對于定子反電動勢中同樣幅值的頻率成分，低次諧波在ψs1中比例遠高于開關頻率等高次諧波。另外，ψs2由ψsz經低通濾波器得到，開關頻率等高次諧波在ψs2中比例較小，因此低次諧波在估算磁鏈中占的比重更大，即頻率越低，其對估算磁鏈影響越大。

綜上所述，考慮到定子反電動勢中諧波含量時，若限幅值較小，則定子磁鏈諧波含量較小，但是位置和幅值估計誤差大；若限幅值較大，則定子磁鏈中含有較大的直流分量，導致幅值和位置估計誤差在零附近以基波頻率脈動；若限幅值為實際磁鏈幅值，則由于定子反電動勢諧波影響輸出磁鏈處于時而限幅時而未限幅狀態，導致定子磁鏈諧波增加。因此限幅值的選取需在諧波含量與位置誤差間作平衡。基于以上分析，本文提出小限幅值加角度補償法，即設置 kL＜1，使穩態一直處于限幅狀態，再用誤差分析式（12）進行角度補償，將可綜合kL＜1和kL=1優點，同時達到較小的諧波和估算誤差。

由于磁鏈位置積分器估算的轉子磁鏈位置用于得到坐標變換定向角，因此估算位置精度直接影響到轉矩的控制精度，估算磁鏈中的諧波將影響定向角諧波，進而影響定子電流的諧波含量。因此當kL＜1時，轉矩穩態誤差較大，但定子電流的諧波含量較小；當kL=1時，轉矩穩態控制精度較高，定子電流諧波含量較適中；當 kL＞1時，轉矩穩態控制精度較好，但定子電流含有較為明顯的直流和2次諧波。而采用本文所提出的小限幅值加角度補償方法可綜合kL＜1和kL=1的優點，同時達到較佳的轉矩控制精度和較好的定子電流波形質量。

4 實驗驗證

為對所提限幅值設置方法進行驗證，本文將其分別應用于25kW和2MW永磁風力發電機的無傳感器控制中，電機參數見表 2。其中小功率實驗平臺易于安裝編碼器，可進行較為詳盡的研究和實驗驗證。主要用于驗證不同限幅值下的誤差分析公式與特點以及不同限幅值設置的對比實驗。大功率實驗平臺用于驗證其在大功率永磁風力發電機運行的可行性和有效性。考慮到永磁風力發電機運行角頻率范圍以及系統的動態要求，本文將25kW永磁風力發電機ωc設置為255rad/s，2MW永磁風力發電機設置為80rad/s。實驗中轉矩指令給定由模擬風機控制器直接給出。由于實驗采用的 2MW永磁風力發電機為六相雙繞組（繞組I和繞組II）輸出，因此，與之配套搭建的全功率變流實驗樣機采用2臺結構一樣的1MW背靠背雙PWM變流器并聯組成。雙繞組發出的交流電分別通過2臺1MW變流器處理后，接到1臺690V/10kV的升壓變壓器，并入10kV電網。2MW永磁風力發電機實驗平臺難于安裝編碼器，為驗證所提方法的無傳感器控制效果，可使繞組I工作，繞組II不工作，將繞組II作為參考。

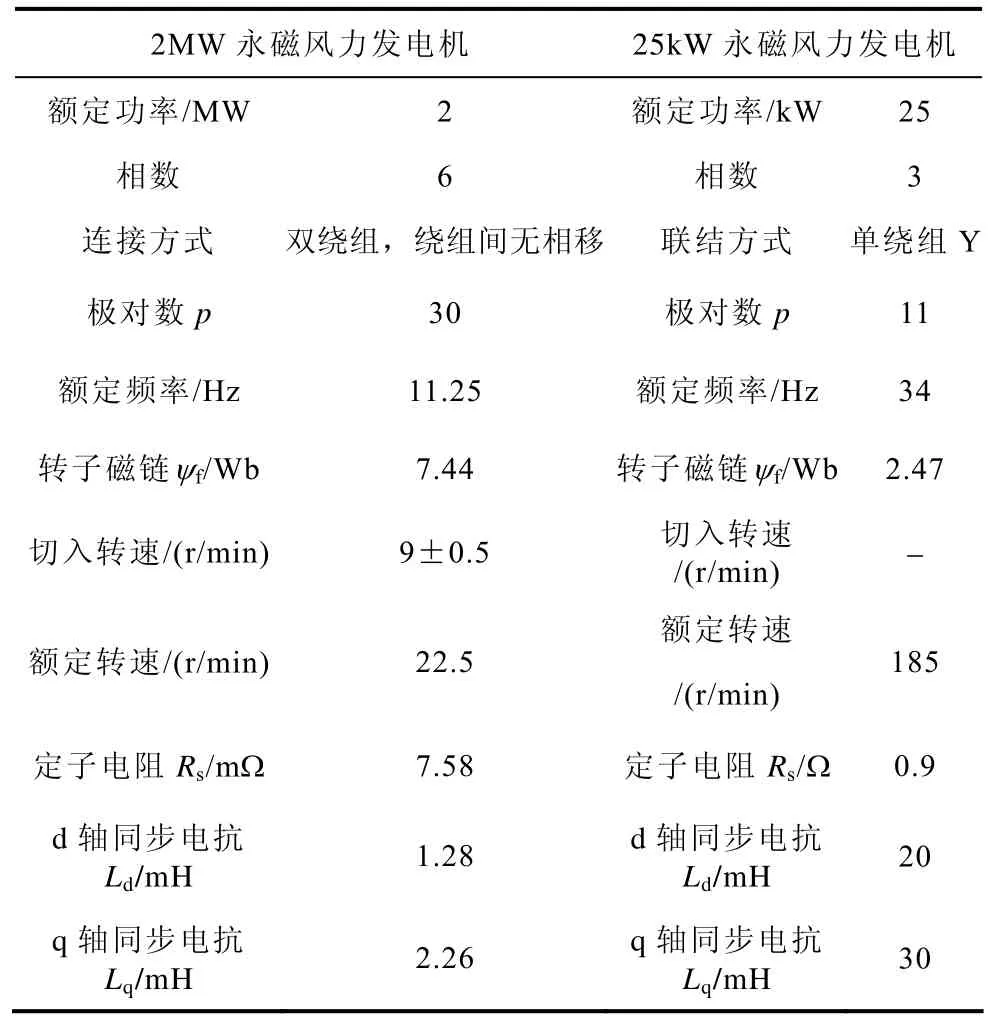
表2 永磁風力發電機參數Tab.2 Parameters of PMSGs

4.1 25kW永磁風力發電機實驗

圖6給出了 25kW 永磁風力發電機運行于70r/min（對應于電機基波頻率分別為 12.83Hz，角頻率80.63rad/s）空載時，應用SFDICT進行磁鏈估算，將 kL分別設置為 0.9、1、1.1時轉子磁鏈位置估算值、實際值（編碼器給出）與估算誤差實驗波形。從kL=0.9波形可見，估算誤差在-13°左右波動，與根據式（12）計算的誤差值-13.35°基本相符。由kL=1可見，轉子磁鏈位置估算誤差較小，基本在0°附近；由kL=1.1波形可見，轉子磁鏈位置估算誤差基本以基波頻率脈動，主要是由于估算磁鏈含有較大的直流分量引起，脈動幅值為6°左右，與理論計算值5.7°基本相符。實驗結果表明了表1誤差分析公式和特點的正確性。

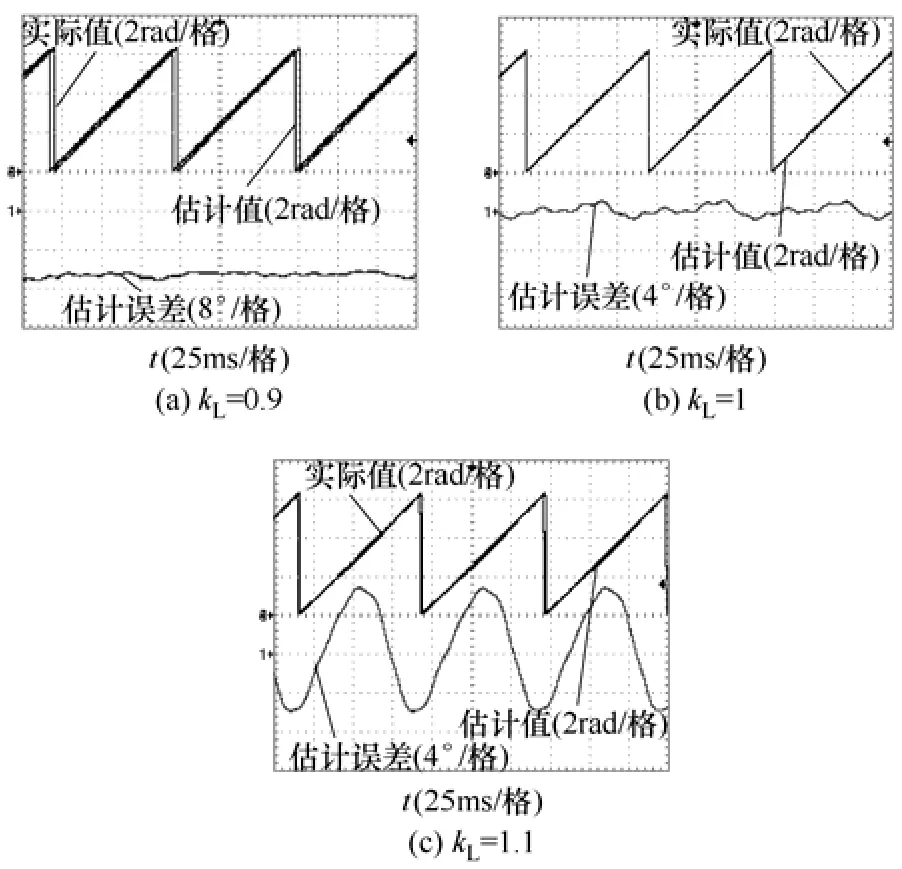
圖6 不同限幅值下空載轉子磁鏈位置估算實驗波形Fig.6 Experimental waveforms of estimated flux linkage position for different kL under no-load conditions

圖7給出了 25kW 永磁風力發電機運行于70r/min，給定轉矩電流設置為-20A（發電為負），將 kL分別設置為 0.9、1、1.1以及 0.9帶角度補償（補償角度為根據式（12）計算的 13.35°）時，轉子磁鏈位置和定子電流諧波分析實驗波形。由前述分析可知，當kL較小時，位置誤差較大，且估算磁鏈超前于實際磁鏈。因此，由圖3可知，負載發電時，將會產生增磁電流，則真實的定子反電動勢、定子磁鏈和功角都會受到影響，而偏離式（12）計算的理論值，考慮這些影響評估負載時位置誤差可根據式（19）計算。以本工況為例，kL=0.9，則定子磁鏈位置估算誤差Δθs=-17.34°，功角估算誤差Δδ= -1.31°，因此總轉子磁鏈位置估算誤差將為-18.65°。從kL=0.9波形可見，估算誤差在-18°左右波動，與理論值-18.65°基本相符；由kL=1和kL=0.9加角度補償波形可見，位置估算誤差較小，基本在0°附近；由kL=1.1波形可見，位置估算誤差基本以基波頻率脈動，脈動幅值為6°左右，與理論計算值5.7°基本相符。從定子電流諧波含量圖可見，THD-F（未計入直流分量）分別為3.73%、4.37%、8.24%、3.56%，直流含量分別為-1.33%、-5.4%、-13.81%、-1.96%，2次諧波含量分別為1.13%、2.08%、7.42%、0.58%。表明當設置 kL＜1時（不論是否加角度補償），定子電流畸變率小；當設置kL=1時，定子電流畸變率較適中；而當設置 kL＞1時，定子電流畸變較大，主要表現在直流和2次分量上。可見采用本文所述的小限幅值加角度補償方式。可同時達到較好的定子電流質量和較小位置誤差。

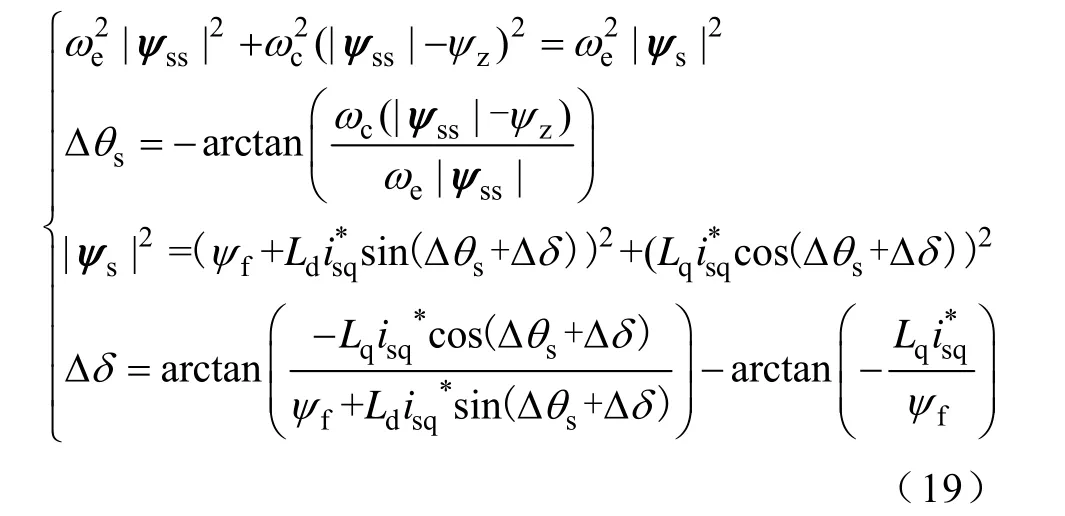
4.2 2MW永磁風力發電機實驗

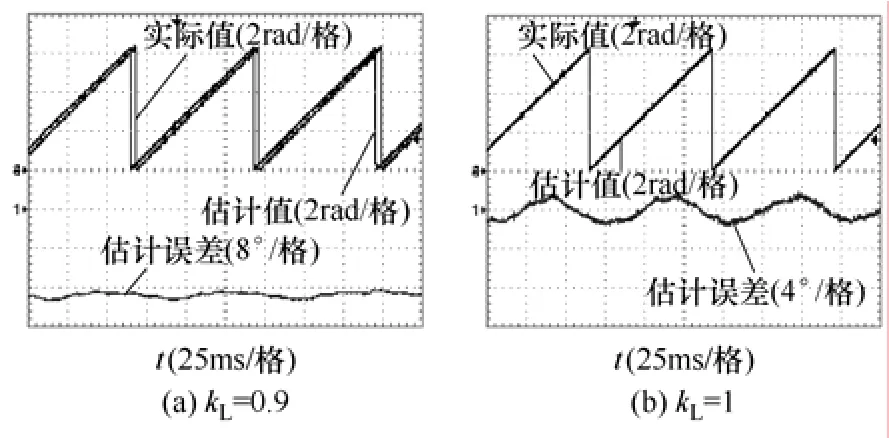
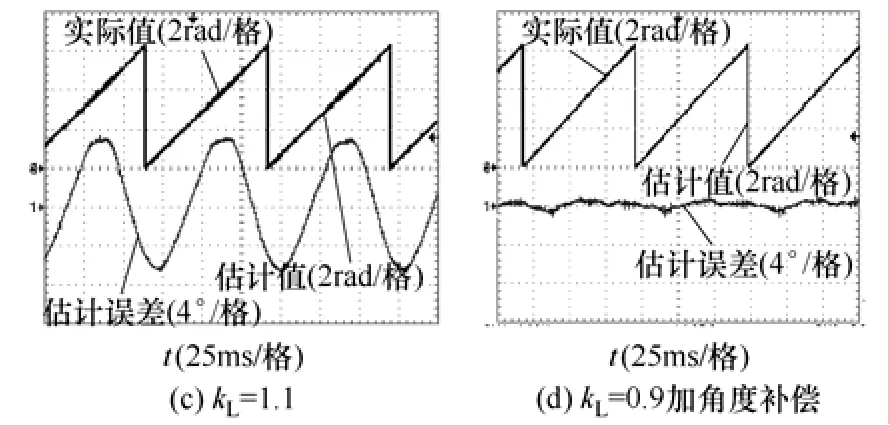
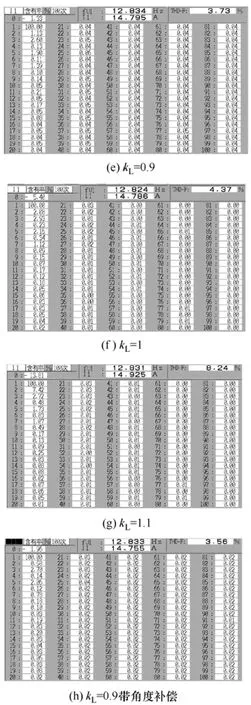
圖7 不同限幅值下帶載轉子磁鏈位置估算波形與定子電流諧波圖Fig.7 Experimental waveforms of estimated flux linkage position and FFT of stator currents for different kL under load conditions

圖8a給出了2MW永磁風力發電機繞組I采用本文所提限幅值設置方法即kL=0.9加角度補償，繞組II采用kL=1時定子電流諧波對比波形。實驗采用功率分析儀Norma4000進行諧波分析，其中，I1為繞組I的A相定子電流，I3為繞組II的A相定子電流。由圖可見，采用小限幅加角度補償法可以得到較好的定子電流質量，而采用kL=1時定子電流中2次諧波含量較明顯。

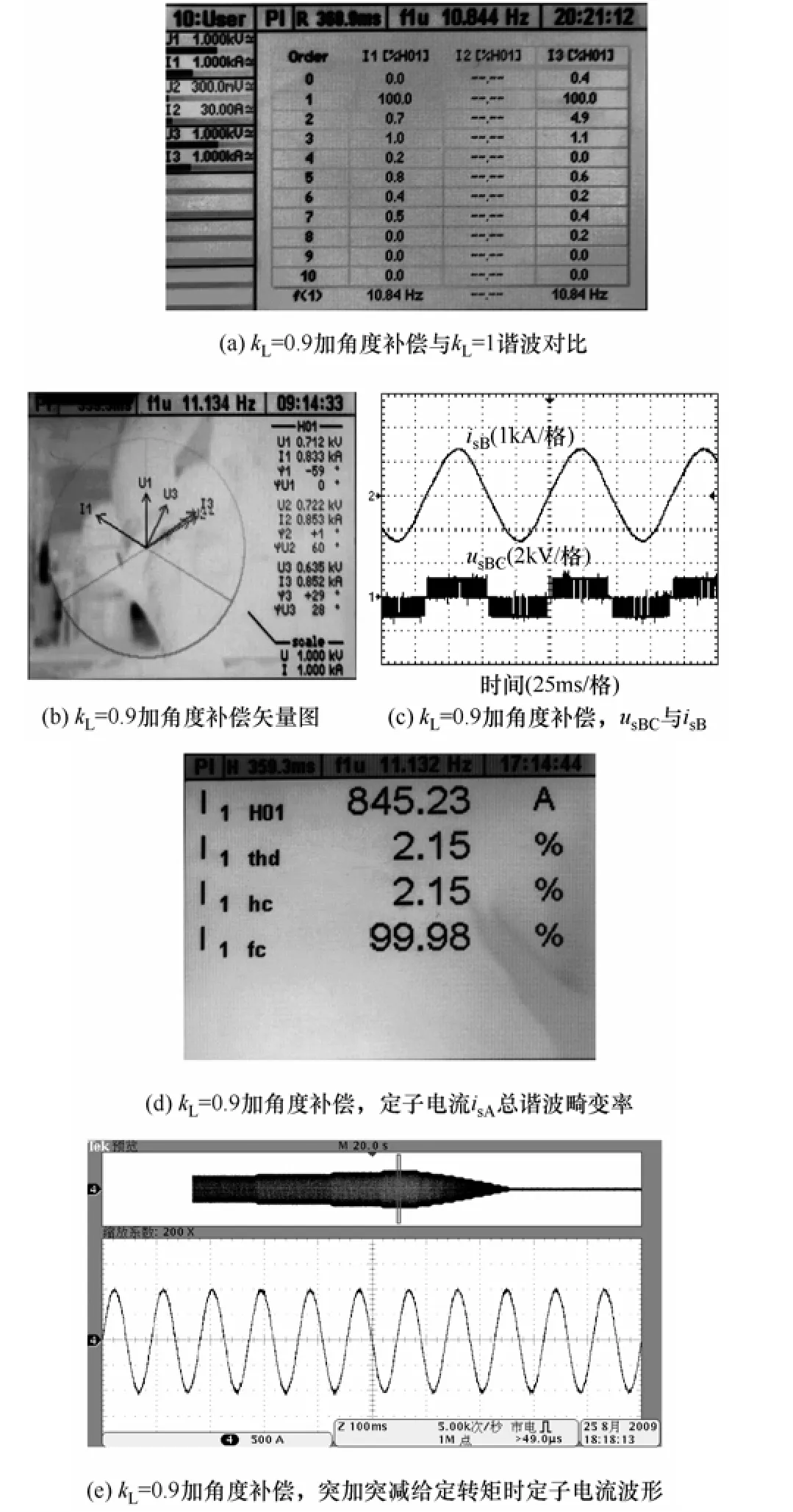
圖8 2MW永磁風力發電機實驗波形Fig.8 Experimental waveforms of 2MW permanent magnet wind generator

圖8b給出了2MW永磁風力發電機運行于額定轉速 22.5r/min，給定轉矩電流峰值為-1 200A，繞組I采用本文所提限幅值設置方法即kL=0.9加角度補償，繞組 II不工作時用功率分析儀 Norma4000測得的矢量波形，其中U1、U2分別為繞組I定子電壓UsAC、UsBC，U3為繞組II定子空載電壓EsBC，I1為繞組I定子電流IsA，I2、I3均為繞組I定子電流IsB，電流均取發電方向為正。由圖可見，U3（即EsBC）超前繞組 I定子電流 I3（即 IsB）29°，即 IsB與 EsB基本同相，轉子磁鏈位置估計的穩態誤差在5°以內。圖 8c給出了定子電壓 usBC和定子電流 isB的穩態波形，圖8d為用Norma4000測得的定子電流isA的總諧波畸變率 THD為2.15%，定子電流穩態電流波形畸變較小。圖8e是額定轉速下，突加突減轉矩給定指令（對應定子電流指令突加突減）時,其中一臺定子電流isB波形，可見，定子電流均能很好的跟蹤轉矩指令的變化。

綜上所述，基于SFDICT磁鏈位置積分器的直驅永磁風力發電機無傳感器控制采用本文提出的小限幅值加角度補償的設置方法時，可同時達到較佳的控制精度和較小的定子電流諧波，具有較好的轉矩動、穩態跟蹤性能且工程實現較為簡單。

5 結論

針對兆瓦級直驅永磁風力發電機特點，本文采用基于SFDICT磁鏈位置積分器的無傳感器控制。通過分析SFDICT在不同諧波含量、不同限幅值下的工作特性，提出了SFDICT在不同限幅值下的誤差分析公式。在此基礎上提出小限幅值加角度補償的磁鏈估算方法，設置SFDICT限幅值低于實際基波磁鏈值，使穩態一直處于限幅狀態，再用誤差分析公式進行角度補償。最后對該方法進行了實驗驗證，結果表明，其仍具有較佳的轉矩動、穩態性能同時具有較好的定子電流質量且工程實現簡單。

[1]Polinder H, de Haan S W R, Dubois M R, et al.Basic operation principles and electrical conversion system of wind turbines[J].Energy and Power Engineering,2005, 15(4): 43-50.

[2]Li H, Chen Z.Overview of different wind generator systems and their comparisons[J].IET Renewable Power Generation, 2008, 2(2): 123-138.

[3]薛玉石, 韓力, 李輝.直驅永磁同步風力發電機組研究現狀與發展前景[J].電機與控制應用, 2008,35(4): 1-5, 21.Xue Yushi, Han Li, Li Hui.Overview on direct-drive permanent magnet synchronous generator for wind power[J].Electric Machines & Control Application,2008, 35(4): 1-5, 21.

[4]Liserre M, Cardenas R, Molinas M, et al.Overview of Multi-MW Wind Turbines and Wind Parks[J].IEEE Transactions on Industrial Electronics, 2011, 58(4):1081-1095.

[5]汪令祥, 張興, 張崇巍, 等.基于位置觀測的直驅系統無速度傳感器技術[J].電力系統自動化, 2008,32(12): 78-82.Wang Lingxiang, Zhang Xing, Zhang Chongwei, et al.A sensorless control method for direct drive wind turbines based on position observation[J].Automation of Electric Power Systems, 2008, 32(12): 78-82.

[6]胡書舉, 王劍飛, 趙棟利, 等.無速度傳感器控制永磁直驅風電變流器的研制[J].電機與控制學報,2009, 13(1): 67-72.Hu Shuju, Wang Jianfei, Zhao Dongli, et al.Development on sensorless control based Back-to-Back converter for direct-driven WECS using PMSG[J].Electric Machines & Control, 2009, 13(1): 67-72.

[7]唐芬, 金新民, 姜久春, 等.兆瓦級直驅型永磁風力發電機無位置傳感器控制[J].電工技術學報,2011, 26(4): 19-25.Tang Fen, Jin Xinmin, Jiang Jiuchun, et al.Sensorless control of MW-level direct-drive permanent magnet wind generator[J].Transactions of China Electrotechnical Society, 2011,26(4): 19-25.

[8]陳瑤.直驅型風力發電系統全功率并網變流技術的研究[D].北京: 北京交通大學, 2008.

[9]Hu J, Wu B.New integration algorithms for estimating motor flux over a wide speed range[J].IEEE Transaction on Power Electronics, 1998, 13(1):125-133.

[10]賈洪平.PMSM DTC無傳感器運行及傳感器集成研究[D].杭州: 浙江大學, 2006.

[11]劉軍鋒, 李葉松, 萬淑蕓.基于 U-I模型的感應電機定子磁鏈觀測方法研究[J].電氣傳動, 2008,38(4): 20-24.Liu Junfeng, Li Yesong, Wan Shuyun.Research of induction motor stator flux observation method based on U-I model[J].Electric Drive, 2008, 38(4)：20-24.