初級永磁型游標直線電機設計與靜態特性分析

杜 懌 程 明 鄒國棠

（1.東南大學電氣工程學院 南京 210096 2.江蘇大學電氣信息工程學院 鎮江 212013 3.香港大學電機電子工程系 香港）

1 引言

隨著能源危機和環境問題的日益凸顯，可再生能源的開發利用正呈現加速發展的趨勢。海浪能以其資源總量大、環境污染低和可持續性強等特點受到了人們的普遍關注。傳統海浪能發電系統大多借助液壓、氣動等機械裝置，先將海浪的直線往復運動轉換成旋轉運動，然后驅動傳統旋轉發電機進行能量轉換[1]，必要時還需采用機械齒輪進行調速，以滿足高速發電機的運行需求。由于使用了大量的中間轉換環節，傳統海浪能發電系統不可避免地存在機械損耗大，功率密度低，可靠性差和需要定期維護等缺點。直驅式海浪發電系統直接利用海浪的直線運動驅動直線發電機，取消了傳統發電系統中的直線-旋轉變換裝置，簡化了系統的結構，從而系統的可靠性、效率和功率密度都能得到相應的提高和改善[2]。目前，國內外學者對直驅式海浪發電機的研究主要集中于永磁同步直線電機（Linear Permanent Magnet Synchronous Machine，LPMSM）[3-5]，也有開關磁阻直線電機（Linear Switched Reluctance Machine，LSRM）的相關報道[6]。然而，由于海浪的起伏速度僅為0.5～2m/s，導致由海浪直接驅動的直線電機運行速度較低，所以直驅式海浪發電機本身往往存在體積大、功率密度低、制造成本高、不利于運輸和安裝等問題。事實上，在確定的功率和速度情況下，電機的體積與電機能產生的轉矩/力密度有直接關系[7]，因此設計低速、大推力直線電機成了改善直驅式海浪發電系統性能的關鍵技術之一。

橫向磁通永磁（Transverse Flux Permanent Magnet，TFPM）電機是一種新型永磁電機，具有很高的推力密度[8]，并被許多學者認為是直驅式系統的首選電機之一。然而，TFPM電機所特有的三維拓撲結構和磁路大大增加了電機設計和制造的難度，同時也限制了傳統疊片技術在該電機中的應用。文獻[9]提出了一種新型同軸式結構的磁齒輪，利用調磁環的調制作用產生波長長、運行速度快的諧波磁場（本文中將這種現象稱為磁齒輪效應），實現機械能在齒輪初級和次級之間進行無接觸、高效地變速傳輸。在此基礎上，文獻[10-12]將一臺外轉子高速無刷直流電機和一臺磁齒輪整合在一起構成磁齒輪復合永磁（Magnetic-Geared Permanent Magnet，MGPM）電機，同時實現了高速電機設計與控制和低速、大轉矩輸出。但由于該電機具有三層氣隙和兩個旋轉部分，給電機設計與制造增加了難度。游標電機[13]利用定子齒凸極對磁場進行調制，通過產生的高速諧波磁場實現電機的低速、大轉矩輸出，但該電機的永磁體位于電機轉子，給永磁體的冷卻帶來較大的困難，容易在高溫工況發生不可逆退磁，并破壞了電機轉子的整體性，降低了電機的可靠性。文獻[7]提出的游標混合(Vernier Hybrid，VH)電機中，永磁體和繞組均被安裝于電機定子，利用電機轉子凸極改變氣隙磁阻以提高電機的轉矩密度，克服了傳統永磁游標電機的缺點，文獻[14]利用三個單相VH電機錯開120°電角度的組合方式，構成一個三相直線電機，獲得了較高的推力密度，但該結構大大降低了電機初級的牢固程度，其采用的集中繞組方式，則大大降低了“磁齒輪效應”變速效果。

本文提出一種新型初級永磁型游標直線（Linear Primary PM Vernier, LPPMV）電機，在詳細分析該新型電機工作原理的基礎上，利用等效磁路法給出了該電機的功率尺寸方程[15]，為電機的初步設計提供了一種有效方法和思路，并利用有限元方法（Finite Element Method，FEM）研究了電機的空載磁鏈、感應電動勢、電感、定位力和推力等靜態特性，理論分析和樣機實驗結果驗證了設計方案的有效性和正確性。

2 電機結構

本文對一臺三相6/2極LPPMV電機展開研究，圖1為其截面圖。電機初級由硅鋼沖片疊成的初級鐵心、三相電樞繞組以及永磁體組成。為了便于繞線，初級鐵心采用半閉口槽設計，永磁體貼裝于初級齒表面。電機次級僅由帶有凸極的硅鋼沖片疊成，既無永磁體，也無繞組，因此，電機次級具有較高的機械強度，十分適合運行于大推力工況。

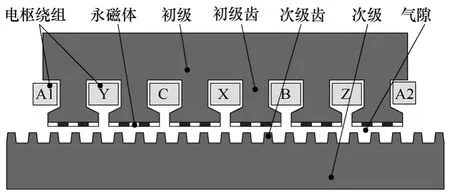
圖1 6/2極LPPMV電機截面圖Fig.1 The cross-section of the 6/2-pole LPPMV machine

雖然新型 LPPMV電機外形上與磁通反向永磁（Flux Revesal Permament Magnet，FRPM）電機[16]十分相似，但兩者的運行原理和設計方法卻完全不同。LPPMV電機的次級凸極鐵心形成交替變化的氣隙磁導，利用該磁導與永磁磁通的相對運動，調制出快速運行的諧波磁場，以提高電機的空載感應電動勢和電磁推力密度，屬于變磁阻永磁（Variable Reluctance Permanent Magnet，VRPM）電機的一種。考慮到永磁體的磁導率與空氣近似相等，取相鄰兩個初級齒極靴之間的空隙寬度與永磁體寬度相等，相鄰兩個初級齒上靠近的兩塊永磁體充磁方向相同，以便在氣隙中產生正弦的永磁磁通。

3 運行原理

為清楚說明新型 LPPMV電機的運行原理，本文采用等效磁路法對電機的氣隙磁通密度進行詳細地推導，并以此得到電機的功率尺寸方程。為了簡化推導過程，本文做了一些必要的假設：

（1）鐵心的磁導率為無窮大。

（2）永磁體的相對磁導率為1。

（3）磁場僅在y方向發生變化，如圖2所示。

（4）忽略漏磁。

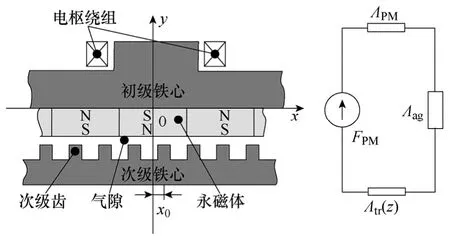
圖2 LPPMV電機的等效磁路模型Fig.2 Model and equivalent magnetic circuit of the LPPMV machine

3.1 氣隙磁通密度

現代永磁體釹鐵硼的退磁曲線呈線性變化，其第二象限的特性可以認為是一條直線[17]，因此，永磁體可以等效成一個恒磁動勢源FPM與一個恒定的內磁導ΛPM相串聯的磁動勢源，在此基礎上得到如圖2所示的LPPMV電機的等效磁路模型。其中，電機磁路單位面積上的總磁導可以表示為

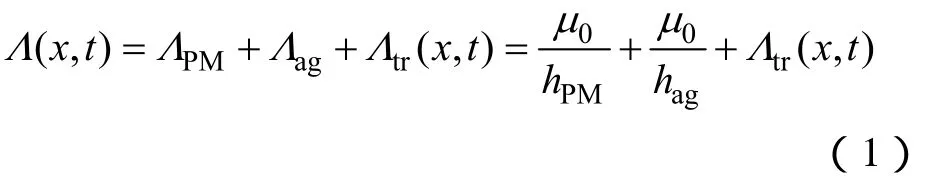
式中，ΛPM，Λag—永磁體和氣隙單位面積磁導；

Λtr(x,t)—由電機次級的齒槽形成的單位面積磁導，它是一個關于位置x和時間t的函數；

hPM—永磁體厚度；

hag—氣隙厚度；

μ0—真空磁導率。

根據式（1）和上述假設，Λ(x,t)可以用圖 3來表示，并可以分解為傅里葉級數形式

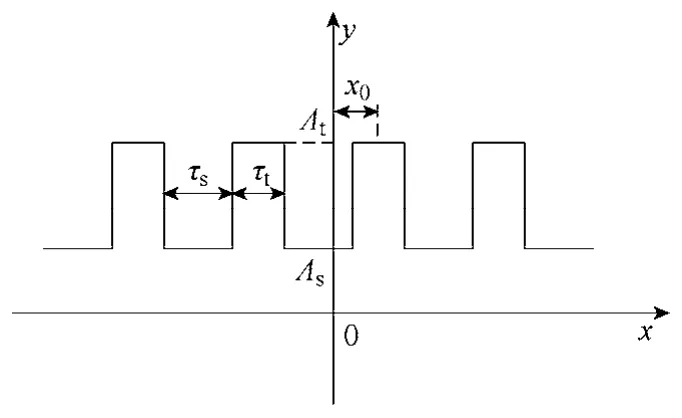
圖3 電機總磁導波形Fig.3 Magnetic permeance waveform

式中 Λ0—磁導中的直流分量；

La—電機初級長度；

vt—次級的運動速度；

x0—次級初始位置；

Nt—次級有效齒數；

Λt，Λs—次級齒和槽范圍內的磁導；

τt，τs—次級齒和槽的寬度；

ht—次級齒高。

此外，貼裝于初級齒表面的永磁體產生的磁動勢FPM也可以使用傅里葉級數的形式表示為

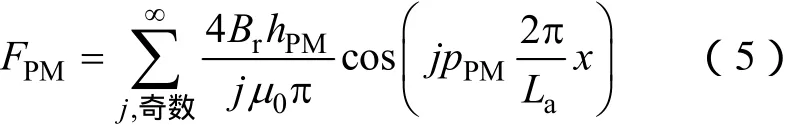
式中 Br—永磁體剩磁；

pPM—永磁磁通的極對數。

忽略高次諧波的影響，僅考慮式（2）和式（5）的直流和基波分量，則電機空載氣隙磁通密度 Bag可近似表示為

式（6）中的第一項由永磁體直接產生，由于LPPMV電機中永磁體貼裝于初級齒表面，因此，該分量并不隨電機次級的運動發生變化，所以不能在電樞繞組中產生感應電動勢；第二項和第三項均由永磁磁通經次級凸極調制產生，其中前者所表示的磁通波長短，運行速度慢，而后者則具有波長長，運行速度快的特點，根據電機學原理，電機的感應電動勢幅值和頻率與磁通的變化速度呈正比，因此選擇第三項作為 LPPMV電機有效諧波分量，有利于提高電機的感應電動勢，進而提高電機的推力密度。由式（6）分析可得有效諧波磁通的極對數pflux和運行速度vflux的關系為

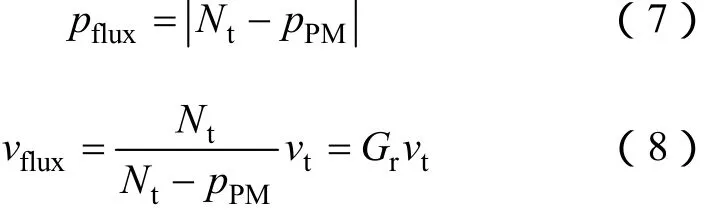
由式（7）可見，與普通電機不同，新型LPPMV電機中同時具有次級凸極齒數Nt、永磁體產生的永磁磁通極對數 pPM和有效諧波磁通極對數 pflux三個參數，且通常三者均不相等，本文所研究的 6/2極樣機的定子齒數為6，有效諧波磁通極數為2。由式（8），有效諧波磁通的運行速度較次級運行速度放大 Gr倍，Gr稱之為磁齒輪變比。此外，當 Nt＞pPM時，vflux和vt同向，反之，則反向。為了獲得最大限度的放大倍數，通常取 pflux=1，電樞繞組則可以按照該有效諧波磁通的極對數進行繞制（這也是該新型電機與FRPM電機結構上的最大區別所在），此外需要將次級凸極數設計的盡可能的大，但另一方面，永磁體之間的極間漏磁會隨著 Nt增大而變大，因此需要綜合考慮之后選取合適的Nt。

由式（6）還可知，有效諧波磁通密度的幅值跟Λ1的幅值成正比，因此可以通過增大Λ1實現增加有效氣隙磁通密度的目的。由式（4）不難發現，有兩種方法可以提高Λ1幅值：

（1）增加次級凸極高度 ht，以增加Λt和Λs之間的差值。

（2）設計次級凸極齒和槽的寬度比為 1，即τt=τs。

3.2 功率方程

新型 LPPMV電機利用運行速度較快的磁場諧波作為勵磁，因此可以將 LPPMV電機看成一臺具有接近正弦感應電動勢波形的普通PMSM，控制電樞中的電流為正弦且與感應電動勢保持同相以取得最大的電磁推力，從而最大限度地將機械能轉換成電能。不考慮電樞電阻的條件下，其電磁功率P可以表達為

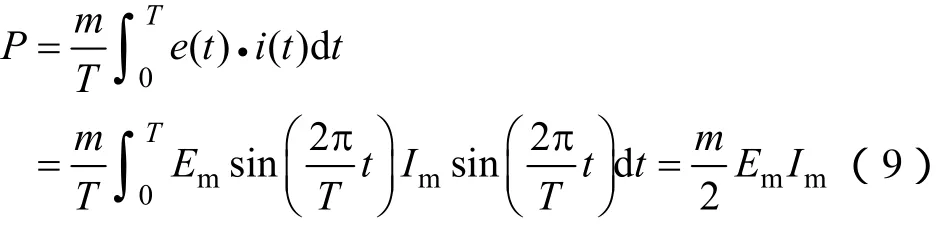
式中 T—感應電動勢和電流的周期；

e(t)，i(t)—感應電動勢和電流瞬時值；

Em，Im—感應電動勢和電樞電流的幅值。

假設電機單相永磁磁鏈為ψpPM，則單相感應電動勢可以表示為

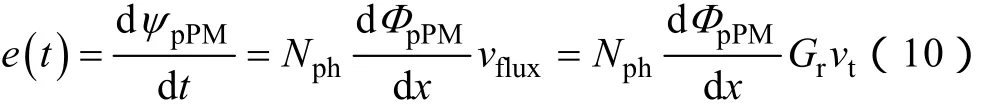
式中 ΦpPM—每相永磁磁通；

Nph—每相繞組匝數。

假設ΦpPM為正弦分布，且滿足如下表達式

式中 τflux—有效諧波磁通的極距，且τflux=La/pflux/2；

Φm—每相永磁磁通峰值。

將式（11）代入式（10），可得

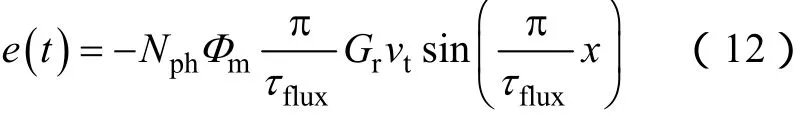
因此感應電動勢的峰值滿足

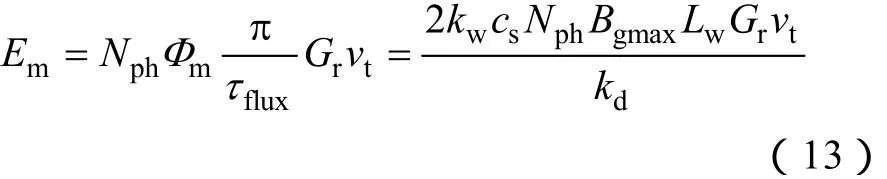
式中 kw—繞組系數；

kd—漏磁系數；

cs—初級齒極弧系數；

Bgmax—有效諧波磁通密度幅值；

Lw—電機寬度。

另一方面，每相正弦分布的電流峰值Im滿足

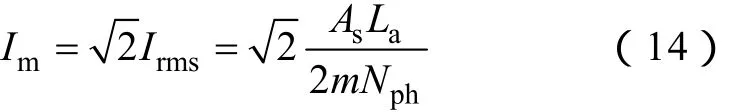
式中 As—電機線負荷。

將式（13）和式（14）代入式（9），可以得到LPPMV電機的功率方程為

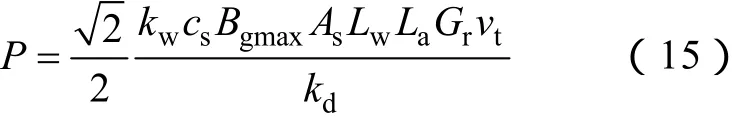
忽略電樞繞組的電阻，P為發電機的有功功率，由于采取了id=0的控制策略，電機電樞反應電抗所需的虛功由直流側電源提供。此時電機的電磁推力可以表示為

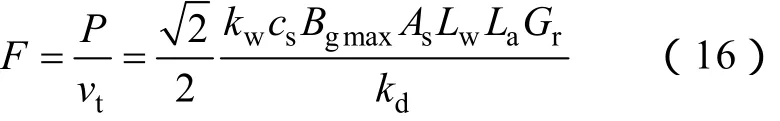
可見，LPPMV電機的電磁推力與電機氣隙面積以及磁齒輪效應的放大倍數Gr成正比。與普通永磁同步電機相比，雖然 LPPMV電機中使用的有效諧波磁通密度幅值要小的多，但只要確保 Bgmax與 Gr的乘積足夠大，就能得到較高的電磁推力密度。

4 電機主要參數計算

根據以上分析，由式（15）可以得到 LPPMV電機的尺寸方程為

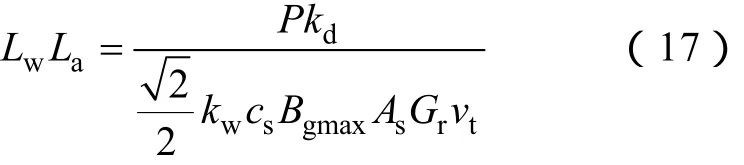
由于本文中初級齒數為6，相數m=3，取pflux=1，則每極每相槽數為1，按照整距進行繞制電樞繞組，繞組因數kw=1。每個初級齒上貼裝5塊永磁體，形成的永磁磁通極對數pPM=18，所以初級齒極弧系數cs=5/6，根據式（7），次級有效凸極數 Nt可以取為17或19，對應的磁齒輪效應放大系數Gr分別為17和 19。顯然 Nt不同取值還將導致不同的漏磁系數kd，因此，其最終的取值取決于Gr和1/kd的乘積，而kd的取值與電機各尺寸都有密不可分的關系，需要使用有限元等數值計算方法，才能得到比較精確的值，根據下文的仿真比較，本文取 Nt=17，此時的漏磁系數 kd=1.724，該漏磁主要由永磁體極間漏磁造成。取次級齒高度 ht=10mm，氣隙厚度 hag=1mm，另外，由式（5），調制前的氣隙磁通密度基波峰值為

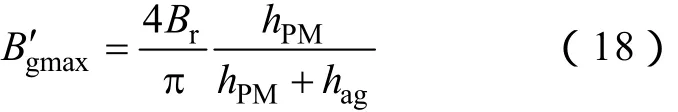
根據經驗，設計Bg′max=1.2T。因此，由式（18）可以算出永磁體厚度hPM。由于LPPMV電機中電樞電流產生的磁通極對數遠遠小于永磁體極對數，即同一個電樞電流磁通極下包括了數塊永磁體，因此永磁體很容易發生不可逆退磁，永磁體厚度不能太小，本文取hPM=4mm。

根據式（6）和3.1節的分析，可得

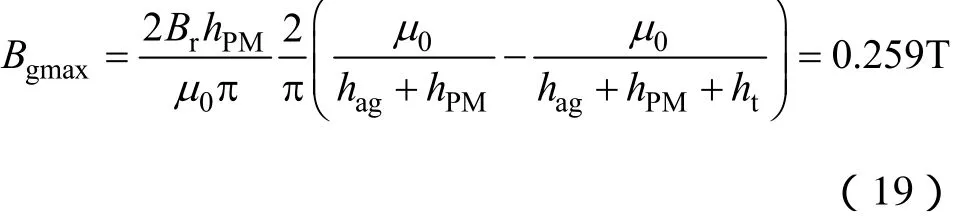
取 As=30 000A/m，當功率 P=1.6kW時，由式（17）可得

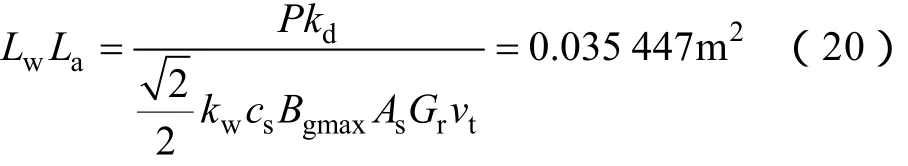
留有一定余量后，取 Lw=0.1m，La=0.36m。此時每塊永磁體的寬度為0.01m。

要求空載感應電動勢幅值為60V，根據式（13），可以算出電樞繞組每相匝數

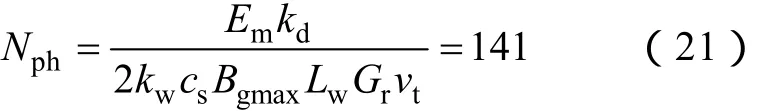
為留有余量，取Nph=142。

5 靜態特性

5.1 永磁磁鏈與感應電動勢

使用二維有限元對所設計的6/2極新型LPPMV電機進行分析，得到電機空載永磁磁鏈和空載感應電動勢與轉子位置角的關系如圖4和圖5所示，表1為空載永磁磁鏈正負半周期的峰值。由于每個初級齒上的永磁體個數為奇數和三相繞組的布置方式存在差異等原因（即A相繞組的正邊位于兩個槽內，分別位于初級兩側的A1和A2，而B、C兩相繞組的正負邊都僅有一個槽，如圖 1中 B-Y，C-Z，位于電樞的中部），導致B、C兩相空載永磁磁鏈存在一個直流偏差，而A相的兩套繞組結構使其直流偏差相互抵消，如圖4和表1所示。但經過求導得到的三相空載感應電動勢卻非常對稱，并且具有很好的正弦度，其總諧波失真度（Total Harmonic Distortion，THD）僅為3%，在額定速度1m/s時，空載感應電動勢幅值為60V，與設計目標相符。

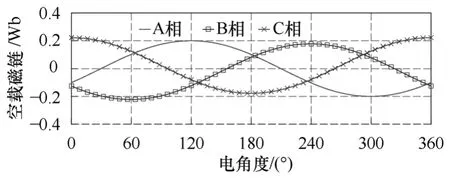
圖4 三相磁鏈波形Fig.4 Flux linkage waveforms

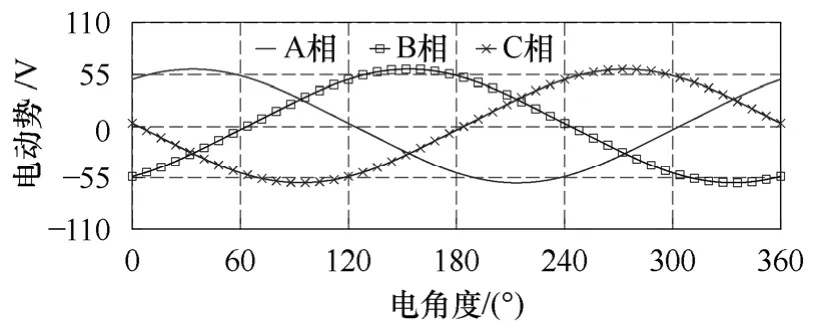
圖5 空載感應電動勢波形Fig.5 No-load EMF waveforms

表1 三相空載磁鏈峰值Tab.1 Peak value of the 3-phase no-load flux linkage（單位：Wb）

5.2 電感

在使用有限元對電機的電感進行計算時，對電樞繞組的某一相通入電流，此時可以得到某相繞組中所匝鏈的總磁鏈為

式中 L—相繞組自感（被測相與通電相為同一相）或互感（被測相與通電相為不同相）；

I—所通入的電流。

根據上式便可以得到繞組的電感

由于永磁體的存在，按照式（23）計算得到的電感稱之為飽和電感，如果計算時將永磁體處理為空氣則可以得到不飽和電感[18]。因為新型 LPPMV電機中的有效工作磁通為總磁通中的某次諧波分量，其幅值較小，所以永磁體對鐵心的飽和程度影響很小，因此本文僅給出了不飽和電感的計算結果，如圖6所示。

圖6 繞組電感波形Fig.6 Winding inductance waveforms

由圖6可知，新型LPPMV電機的電感幾乎不隨轉子位置的發生變化，可以認為在整個電周期中為一恒定值，這一結論在后期電機的控制中非常重要。其次，如上文所述，該電機的三相繞組安排方式的差異性導致A相電感與B、C兩相不同，它是由A1和A2的自感以及A1、A2之間的互感組成，但A1和A2兩者之間并不能完全耦合，導致A相自感相對較小，A、B、C三相互感也因此存在差異。此外，與其他VRPM一樣，LPPMV電機的電感較大，導致該電機作為發電機運行時，需要如3.2節所述由外界提供無功輸入以補償電感所需，以減小發電機的電壓調整率，而當該電機運行于電動狀態時，則需要較大的直流母線電壓以提供電感上的電壓降[7]。

5.3 定位力

定位力是衡量永磁電機性能的重要指標之一，它會對電機的起動性能、電磁推力紋波等產生影響，其周期以機械角度可以表示為

式中 Ncog—永磁同步電機初級齒數與永磁極數的最小公倍數，對于 6/2極電機Ccog=60°。

圖7所示為采用虛功法計算得到的電機定位力波形，其峰峰值為±15N，周期為60°，與式（22）結果相符，表明PMSM的分析方法適用于LPPMV電機。

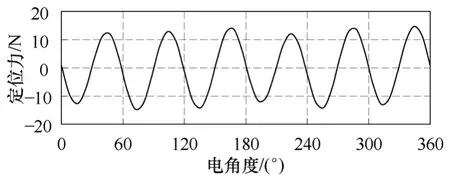
圖7 定位力波形Fig.7 Cogging force waveform

5.4 電磁推力

如上文所述，直驅式系統中直線電機的運動速度一般較低，這就要求電機具有較大的電磁推力密度以減小制造和安裝成本。圖8所示為加載與感應電動勢同相位的電流時，電機電磁推力隨電流有效值的變化曲線。當電流小于額定值時，電磁推力幾乎隨電流呈線性變化，當電流超過13A時，由于磁路飽和，電磁推力增長趨緩。當電流等于額定電流13A時，電磁推力可達 1.6kN，由此計算得到該LPPMV電機的電磁推力密度為44.4kN/m2，遠遠大于普通永磁同步電機的經驗值。

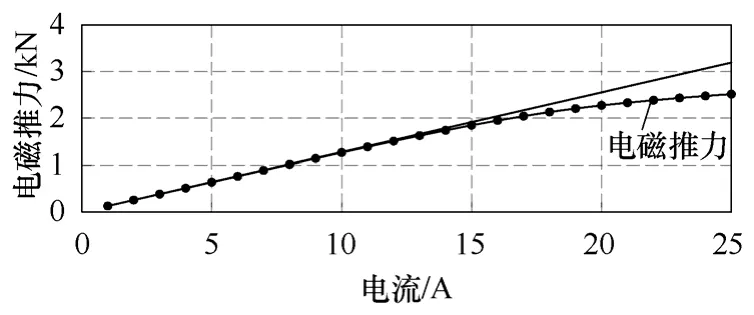
圖8 電磁推力波形Fig.8 Electromagnetic thrust force waveform

6 樣機實驗

為了驗證上述分析的正確性，設計并制造了一臺額定功率為1.6kW的樣機，主要尺寸參數見表 2。其中，槽電流密度的數據按有效銅線部分計算。

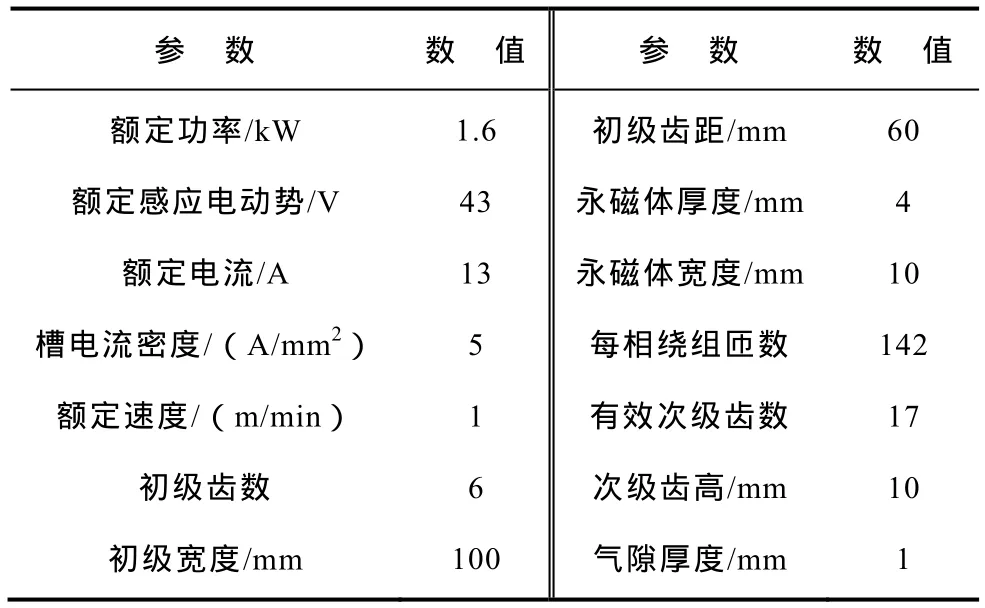
表2 電機參數Tab.2 Machine parameters

圖9為樣機初級及樣機整機的實物照片。在測試初期，為了便于實驗，將較長的電機次級設計成電機定子，而較短的初級設計成電機動子。圖 10所示為電機在運行速度為額定速度 1m/s時的空載感應電動勢實測波形，可見三相電動勢基本對稱，THD約為4.04%，其反電動勢峰值約為55V，比圖5所示的仿真值略小，主要原因是二維有限元忽略了電機的端部漏磁等因素的影響。

圖9 LPPMV樣機Fig.9 LPPMV prototype

圖10 1m/s時間空載感應電動勢實驗波形Fig.10 Measured no-load EMF waveforms at 1m/s

圖11為采用LCR測試儀實測樣機不同位置時三相繞組電感的變化規律，由圖可見，三相電感幾乎不隨電機動子位置發生變化，且A相電感明顯小于 B、C兩相，與上文仿真結果和理論分析相符。此外由于電樞繞組的端部漏感和樣機制作時三相繞組相對初級鐵心的位置不同等因素，使實測電感大于二維仿真值，并使B、C兩相電感與A相電感的差距增大，但仍與仿真值較為接近。

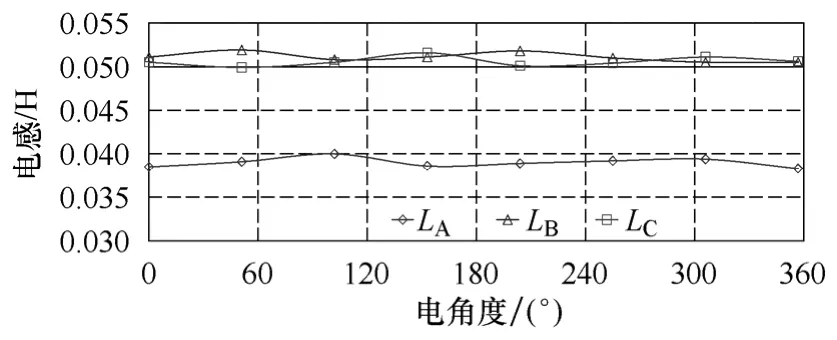
圖11 電感實測波形Fig.11 Measured winding inductance waveforms

7 結論

本文提出并設計了一種新型 LPPMV直驅式直線電機，從氣隙磁通密度著手，展開了該電機的二維磁場計算，詳細分析了工作原理，并由此推導了其功率尺寸方程。通過二維有限元仿真，研究了LPPMV電機的空載磁鏈、感應電動勢、電感、定位力和電磁推力等靜態特性，并制造了實驗樣機，樣機三相空載電動勢和電感測量結果與設計結果吻合。研究表明，基于磁齒輪效應，該電機氣隙中產生波長長、運行速度快的諧波磁場，使其具有較大的空載感應電動勢和電磁推力密度，適宜用于低速工況的直驅式系統，如海浪發電等，但為了得到較大的磁齒輪變比，電機極對數設計得相對較小，導致了 LPPMV電機電感大，且三相電感之間存在差異等問題，作為發電機運行時，需要采取相應的控制策略降低其由電樞反應電抗引起的電壓下降，發揮該電機大推力密度的特點。

[1]Falnes J.A review of wave-energy extraction[J].Marine Structures, 2007, 20(4): 185-201.

[2]游亞戈, 李偉, 劉偉民, 等.海洋能發電技術的發展現狀與前景[J].電力系統自動化, 2010, 34(14):1-12.You Yage, Li Wei, Liu Weimin, et al.Development status and perspective of marine energy conversion systems [J].Automation of Electric Power Systems,2010, 34(14): 1-12.

[3]Wu Feng, Zhang Xiaoping, Ju Ping, et al.Optimal control for AWS-based wave energy conversion system[J].IEEE Transactions on Power Systems,2009, 24(4): 1747-1755.

[4]袁榜, 余海濤, 胡敏強.用于海浪發電永磁圓筒型直線發電機的結構優化與分析[J].微電機, 2011,44(3): 33-36.Yuan Bang, Yu Haitao, Hu Minqiang.Optimized design and analysis of permanent magnet tubular linear generator[J].Micromotors, 2011, 44(3): 33-36.

[5]Hodgins N, Keysan O, McDonald A S,et al.sign and testing of a linear generator for wave-energy applications[J].IEEE Transactions on Industrial Electronics, 2012, 59(5): 2094-2103.

[6]Du Jinhua, Liang Deliang, Xu Longya, et al.Modeling of a linear switched reluctance machine and drive for wave energy conversion using matrix and tensor approach[J].IEEE Transactions on Magnetics,2010, 46 (6): 1334-1337.

[7]Brooking P R M, Mueller M A.Power conditioning of the output from a linear vernier hybrid permanent magnet generator for use in direct drive wave energy converters[J].IEE Proceedings of Generation,Transmission and Distribution, 2005, 152(5):673-681.

[8]褚文強, 辜承林.新型橫向磁通永磁電機磁場研究[J].中國電機工程學報, 2007, 27(24): 58-62.Chu Wenqiang, Gu Chenglin.Study on magnet field of novel transverse-flux permanent magnet machine[J].Proceedings of the CSEE, 2007, 27(24): 58-62.

[9]Atallah K,Howe D.A novel high-performance magnetic gear[J].IEEE Transactions on Magnetics,2001, 37(4): 2844-2846.

[10]張東, 鄒國棠, 江建中, 等.新型外轉子磁齒輪復合電機的設計與研究[J].中國電機工程學報,2008,28(30): 67-72.Zhang Dong, Chau K T, Jiang Jianzhong, et al.Design and research of a novel magnetic-geared outer-rotor compact machine[J].Proceedings of the CSEE, 2008, 28(30): 67-72.

[11]Chau K T, Zhang D, Jiang J Z, et al.Design of a magnetic-geared outer-rotor permanent-magnet brushless motor for electric vehicles[J].IEEE Transactions on Magnetics, 2007, 43(6): 2504-2506.

[12]Jian L, Chau K T, Jiang J Z.A magnetic-geared outer-rotor permanent-magnet brushless machine for wind power generation[J].IEEE Transactions on Industry Applications, 2009, 45(3): 954-962.

[13]Toba A, Lipo T A.Novel dual-excitation permanent magnet vernier machine[C].IAS Annual Meeting,1999:2539-2544.

[14]Mueller M A, Baker N J.Modelling the performance of the vernier hybrid machine[J].IEE Proceedings of Electric Power Applications, 2003, 150(6): 647-654.

[15]王玉彬，程明，樊英，等.功率分配用雙定子永磁無刷電機設計與電磁特性分析[J].電工技術學報,2010, 25(10): 37-43.Wang Yubin, Cheng Ming, Fan Ying,et al.Design and electromagnetic performance analysis of double stator permanent magnet brushless machine for power splitting[J].Transactions of China Electrotechnical Society, 2010, 25(10): 37-43.

[16]王蕾, 李光友, 張強.磁通反向電機的變網絡等效磁路模型[J].電工技術學報, 2008, 23(8): 18-23.Wang Lei, Li Guangyou, Zhang Qiang.Networkvarying equivalent magnetic circuit modeling of a flux-reversal machine[J].Transactions of China Electrotechnical Society, 2008, 23(8): 18-23.

[17]唐任遠.現代永磁電機理論與設計[M].北京： 機械工業出版社, 1997.

[18]花為, 程明.新型三相磁通切換型雙凸極永磁電機電感特性分析(英文)[J].電工技術學報, 2007,22(11): 21-28.Hua Wei, Cheng Ming.Inductance characteristics of 3-phase flux-switching permanent magnet machine with doubly-salient structure[J].Transactions of China Electrotechnical Society, 2007, 22(11): 21-28.