基于Copula函數的波高與周期長期聯合分布

陳子燊，曹深西

（中山大學 水資源與環境系，廣東 廣州 510275）

波高和周期對海岸和海洋工程建筑物都具有強烈的影響。由于海岸和海洋工程建筑物失事代價很高，探索設計波高和相應周期的長期聯合分布模式，精確地推算其聯合設計水平，對于相關工程的投入與風險管理具有重要的應用價值。已有研究表明，依據現有的《港口工程技術規范》關于重現期設計波高相對應的波浪周期的推算方法來指導工作實踐是不太妥當的。趙耀南（1982）提出采用“等重現期”原則，依據建筑物的耐波特性，選擇產生最大波浪荷載的最不利波高和周期的組合作為設計波浪，但過分強調運行安全將明顯提高建筑物設計標準，增大工程建筑物的資金投入。Ochi（1978）和潘錦娥（1989）曾分別使用對數正態分布擬合波高與周期的長期聯合分布，進而導出平均周期的條件概率密度函數，為推求與多年一遇設計波高相對應的設計平均周期做了重要的探索。方鐘圣等（1989）指出，在給定波高下周期條件平均值與標準差隨波高的變化并不能很好地遵循模式中隱含的對數正態律，利用長期器測波浪資料分析，認為在給定波高下周期的條件特征值的變化規律，其條件平均值和條件標準差隨著波高的變化可用線性回歸式表示，提出一個海洋波高與周期的長期聯合分布的經驗模式。不過，由于采用了一些近似假定，難以確定此聯合分布模式的普適性。為此，應用新的理論與方法更深入地探索設計波高與相應波周期的長期聯合分布問題值得嘗試。本文將以近十多年來已被廣泛應用于金融工程風險和水文氣象極端事件的兩變量聯合分布的Copula函數的理論與方法（Favre etal，2004；Zhang etal，2007；Shiau etal，2007；劉曾美 等，2009；陳子燊 等，2011；Joe，1997），通過實例分析為波高和周期的長期聯合分布模式的計算提供新的選擇。

1 基于Copula函數的聯合概率分布模型

1.1 Copula函數、參數估計和擬合優度評價

根據奠定Copula函數理論基礎的Sklar定理，令F是具有單變量邊緣分布函數F1，…，Fn的n維分布函數，若邊緣分布函數F1，…，Fn連續，則存在一個唯一滿足Fn（xn）關系的連接函數C。反之，如果C是一個n維Copula，且F1，…，Fn為分布函數，則函數F（x1，…，xn）是邊緣分布F1，…，Fn的聯合分布函數。

研究表明（秦振江 等，2007；熊立華 等，2005），基于Copula函數構建多變量聯合概率分布模型有以下突出優點：1）Copula函數能夠把邊緣分布和變量間的相關關系分開處理，因此能夠對邊緣分布靈活選擇，選擇能更好地擬合單變量自身變化規律的邊緣分布；2）Copula函數能夠捕捉隨機變量間的非線性相關關系，且求解較簡單，相對于線性相關提高了適用范圍；3）由Copula函數導出的一系列的相關性度量指標，拓展了變量間的相關性度量范圍，在實際工作中有更加廣泛的應用。因此，實際建模可分兩步進行：首先擇優確定邊緣分布，然后再擇優選擇能更好地反映變量間相關結構的Copula函數構建聯合分布模式。當前廣泛應用于水文氣象領域的兩變量Archimedean族Copula函數有 （Zhang etal，2006）：①Gumbel-Hougaard（GH）Copula函數；②Clayton Copula函數；③Ali-Mikhail-Haq（AMH）Copula函數；④Frank Copula函數。由于使用不同的Copula函數分析結果可能明顯不同，因此可通過Genest-Rivest圖示方法（Genest etal，1993）、均方根誤差（RMSE）準則法和AIC信息準則法等擬合優度檢驗方法擇優選用Copula函數。

1.2 聯合分布、重現期與風險概率

由上述Copula的定義和性質可知，利用二變量Copula函數，歷年最大波高H和相應平均周期T的聯合分布可表示為：

由單變量累積概率分布，可知邊緣分布最大波高H和相應平均周期T的重現期為：

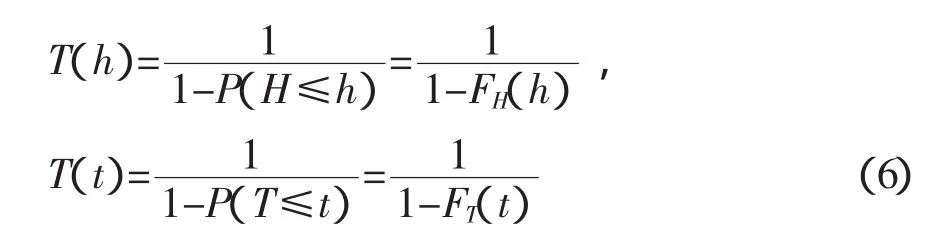
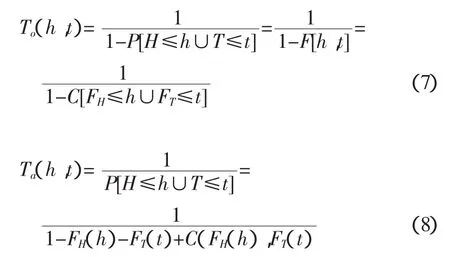
由概率論可導出以下2個條件概率（陳子燊，2011）。條件概率1：

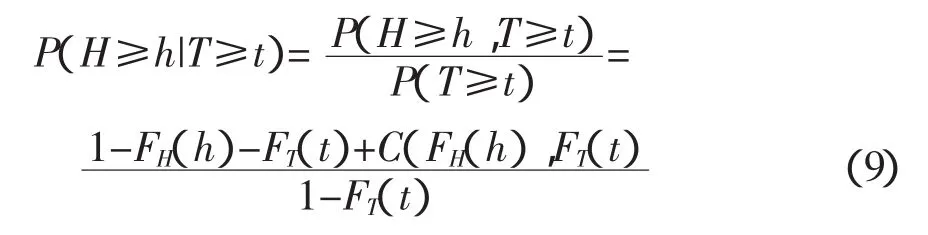
條件概率2：

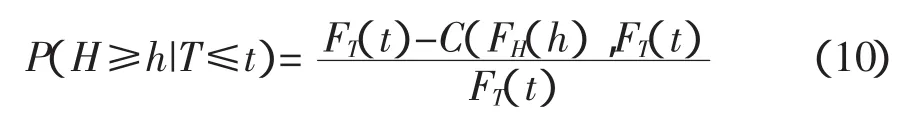
P（H≥h|T≥t）表示當發生超過某一特定周期時，出現超過某一設計波高的概率；P（H≥h|T≤t）表示發生小于某一特定周期時，出現大于某一設計波高的概率。這兩個條件概率屬于超值概率，即可定義為遭遇概率或風險概率，其倒數即為條件（或遭遇）重現期。同理也可計算P（T≥t|H≤h）和P（T≥t|H≤h）的遭遇概率和條件重現期。

2 實例研究

2.1 研究背景與基本數據

實例研究數據采用粵東汕尾海洋觀測站1972-1992年觀測的歷年熱帶氣旋影響期間S向浪的最大波高H1/10與相應的平均波周期T。樣本的基本統計特征值表明，最大波高H1/10為7.3m，相應最大波周期T為8 s。極值波高及其相應波周期的偏態系數分別為0.84和0.11，屬于正偏分布。

2.2 聯合分布計算與分析

2.2.1 邊緣分布函數

對兩樣本的邊緣分布，都使用了以下2個三參數的概率分布函數擇優：

1）廣義極值分布 （GEV）：

閃速爐電收塵設計煙氣量［1］162000m3/h（350℃時）；入口煙氣溫度350℃，出口溫度280℃；入口壓力-2.5kPa，入口含塵量≤90g/m3；出口含塵量≤0.5g/m3；

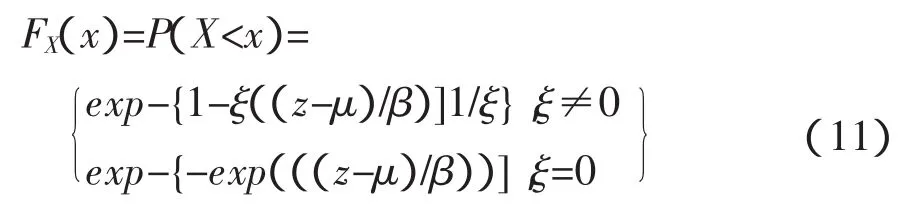
2）皮爾遜三型分布（P-III）：

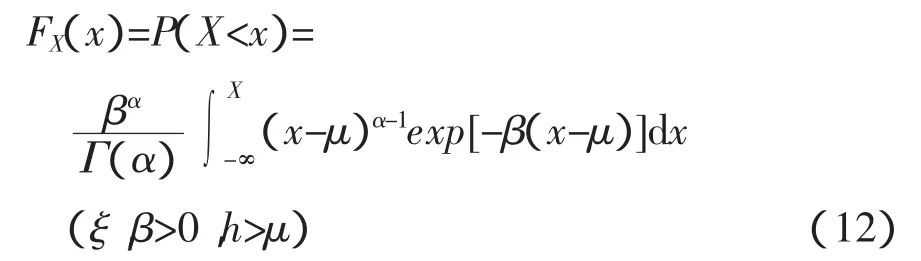
式中，ξ，β，μ分別為形態參數、尺度參數和位置參數。參數估計使用線性矩（L-矩）方法。經驗頻率分布Pi使用Gringorten公式計算：Pi=（i-0.44）/（n+0.12）。擬合結果采用均方根誤差（RMSE）、經驗頻率和理論頻率擬合誤差平方和（Q）和概率點據相關系數（PPCC）檢驗其擬合優度。根據擬合優度檢驗結果（表1）比較，年最大H1/10和相應平均周期T較優邊緣分布分別選用P-III分布和GEV分布（圖1）。

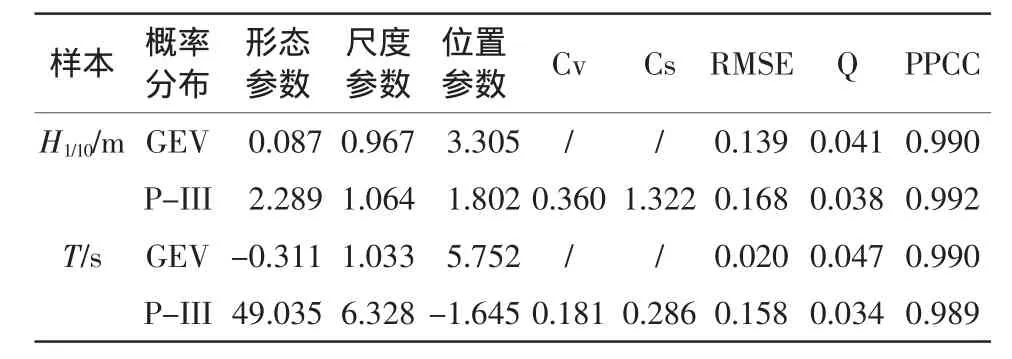
表1 邊緣分布參數與優度檢驗值

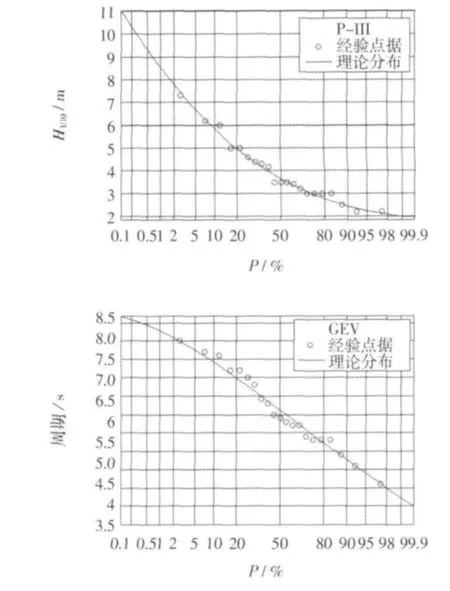
圖1 年最大波高的P-III型分布（上圖）與相應平均周期的廣義極值分布（下圖）

2.2.2 Copula函數的參數估計及擬合優度評價

統計表明，年最大波高和相應周期之間的Spearman相關系數ρ高達0.93，Kendall秩相關系數τ等于0.624，說明二者之間存在高關聯性。采用相關性指標法計算的兩個變量的聯合概率分布copula函數的參數 θ等于 2.658，并利用 AIC、RMSE檢驗其擬合優度，結果見表2。

根據擬合優度評價指標，選擇兩樣本中AIC和RMSE最小、Genest-Rivest圖示方法KT-Ke關系圖中點據和理論直線最接近45°對角線的GH Copu1a函數作為聯合概率分布的連接函數。擇優構建年最大波高和相應周期聯合概率分布模式如下：

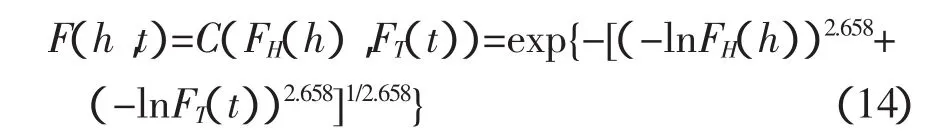
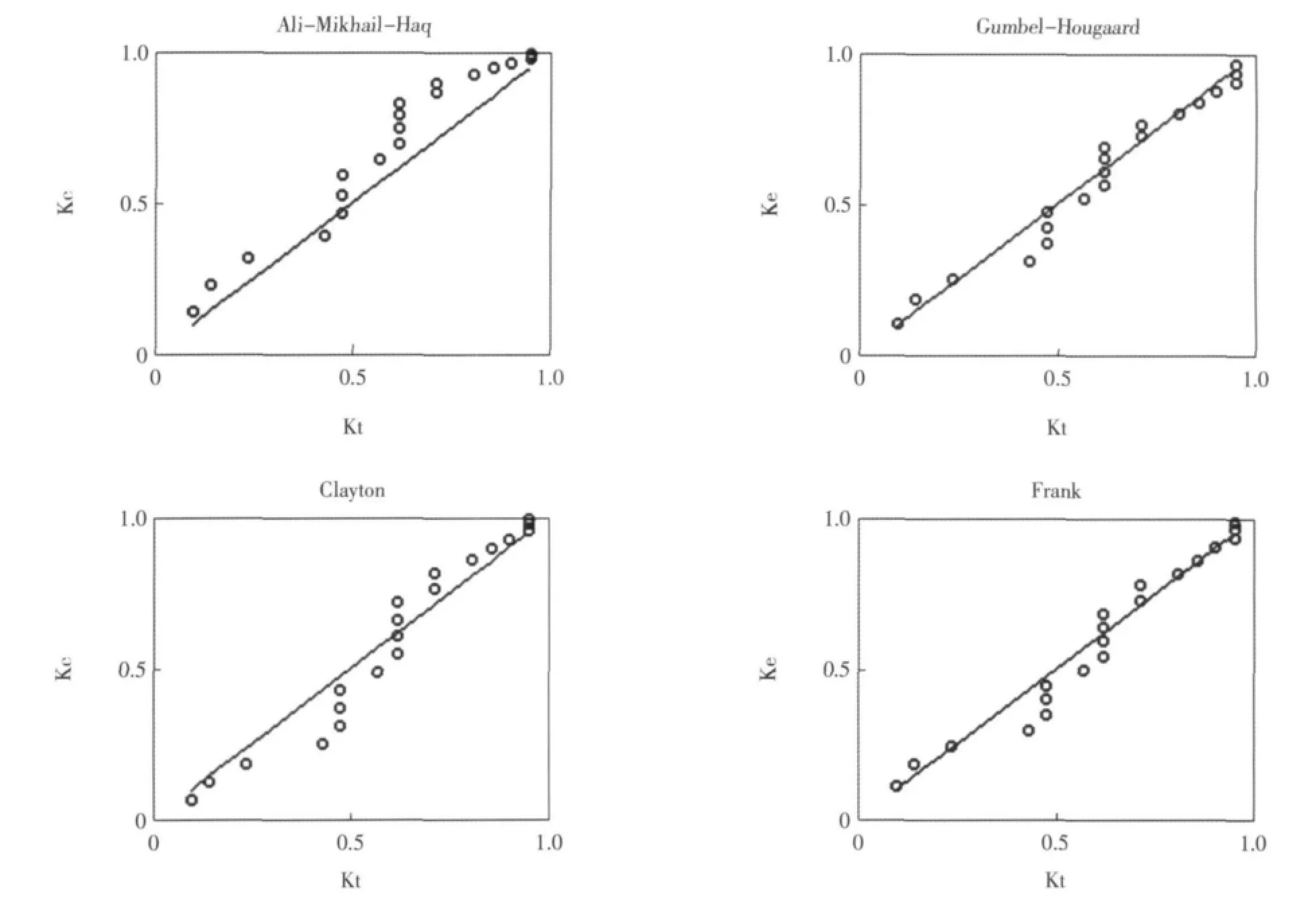
圖2 copula函數擬合對比圖

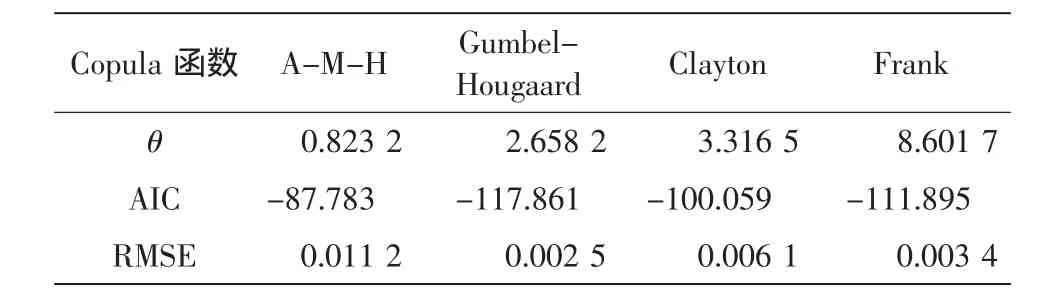
表2 4個Copula函數的參數及其擬合優度指標對比

2.2.3 聯合概率分布與重現期

由二變量GH Copula聯合分布計算的年最大波高和相應平均周期的聯合分布、聯合重現期和同現重現期見圖4所示，不同重現期的設計波高與設計周期見表3。按照同頻率原理 （即，T（0h，t）=T），年最大波高H1/10與相應周期T聯合重現設計值大于單變量邊緣分布推算的設計值，重現期5～100年的設計波高值相對差值大約介于3.3%～5.8%。100年一遇年最大波高H1/10與相應周期T邊緣分布設計值分別為8.5m和8.3 s，而同頻率的聯合分布設計值為8.8m和8.3 s；50年一遇年最大波高H1/10與相應周期T邊緣分布設計值分別為7.8m和8.1 s，同頻率的聯合分布設計值分別為8.0m和8.2 s。兩變量邊緣分布重現期為50年一遇和100年一遇情況下的聯合重現期則分別為39年和77年，同現重現期則分別達71年和142年。此說明，同頻率條件下年最大波高H1/10和相應周期T聯合概率分布的設計標準高于單變量的設計標準，其中波高設計值的差異略大于周期設計值；聯合重現期和同現重現期的設計值可考慮作為海岸海洋工程建筑物波高和周期設計值的上下限。

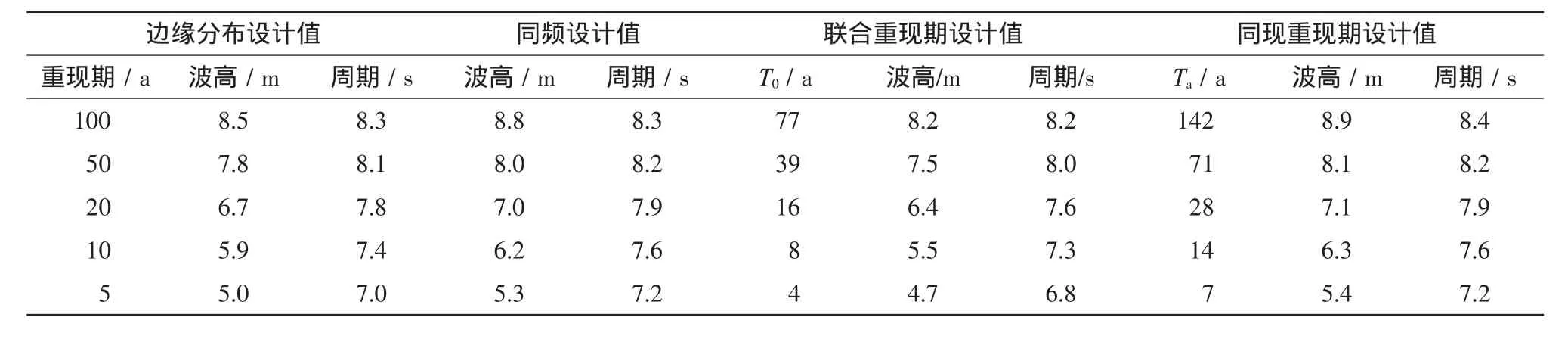
表3 不同重現水平的年最大波高H1/10和相應平均周期T的設計值

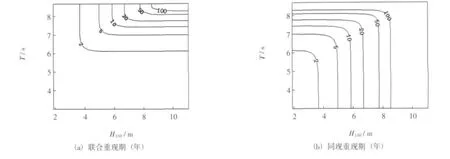
圖3 聯合重現期（年）等值線圖（左圖）和同現重現期（年）等值線圖（右圖）

2.2.4 條件概率分布與遭遇概率

分別計算最大波高H1/10與相應周期T的兩種條件概率：P（H≥h|T≥）t和P（H≥h|T≤）t，計算結果見表4、圖4。

表4顯示，在特定頻率設計波高條件下，隨波高設計頻率的減小，二者的遭遇概率也隨之迅速減小；反之，特定增水設計頻率隨風速條件頻率的減小，二者的遭遇概率隨之明顯增大。條件概率1表明，同頻率下的年最大波高和相應周期的遭遇概率介于70.4%～81.3%。設計頻率2%（重現期50年）的二者的遭遇概率為70.6%（條件重現期1.4年），設計頻率2%的最大波高與設計頻率為1%的相應周期的遭遇概率為88.9%（條件重現期1.1年）。條件概率2顯示，當設計波周期小于某定值時，相對于條件概率1，年最大波高和相應周期的遭遇概率明顯減小，同頻率下年最大波高和相應周期的遭遇概率介于0.3%～18.7%。二變量設計頻率都為2%時，遭遇概率為0.6%（條件重現期167年），設計頻率為2%的最大波高與設計頻率1%的周期的遭遇概率為1.1%（條件重現期89年）。

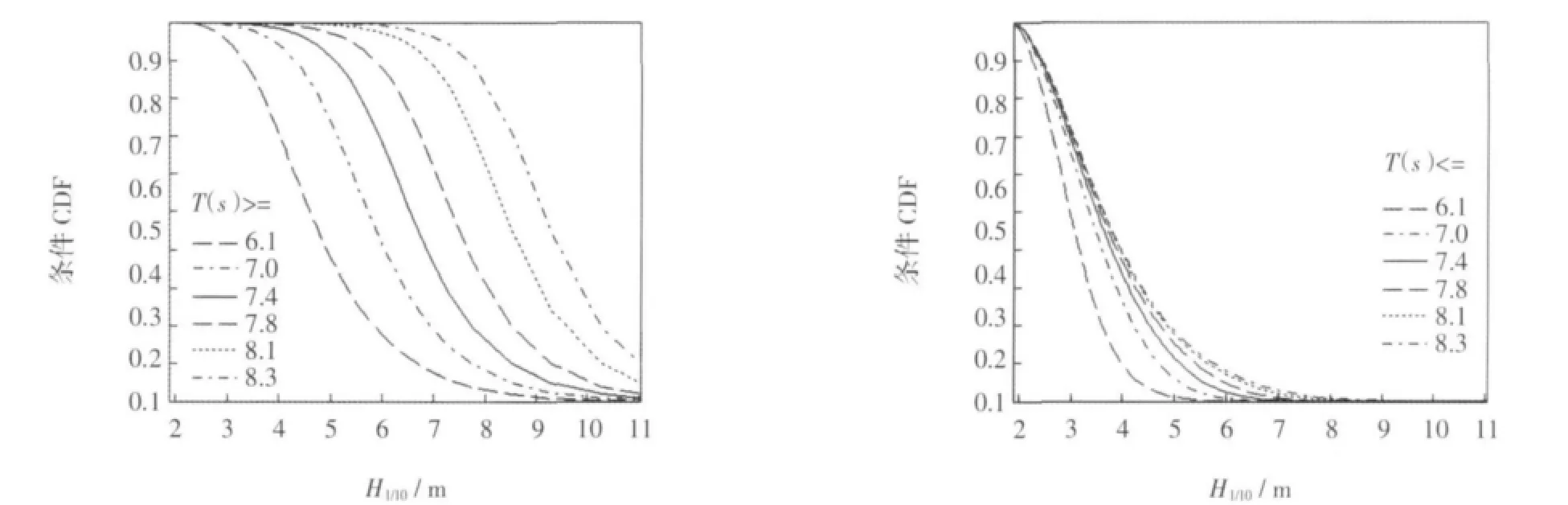
圖4 條件概率1等值線圖（左圖）和條件概率2等值線圖（右圖）

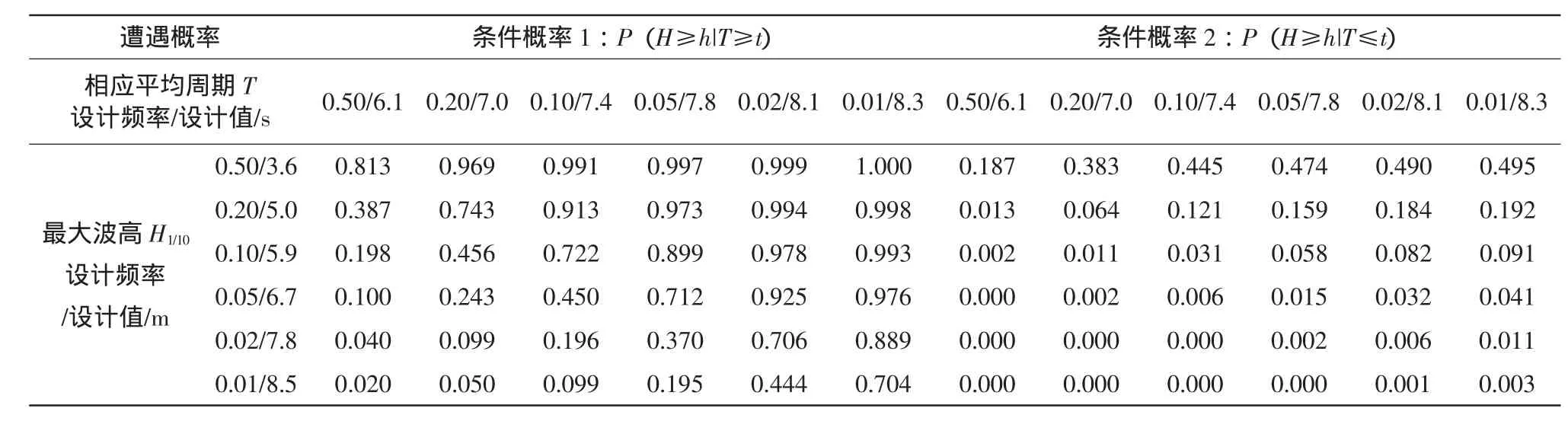
表4 年最大波高和相應平均周期遭遇概率

3 結論

Copula函數作為一個強有力的理論與方法，計算簡便，非常適用于長期聯合分布與風險概率分析。本文對粵東汕尾海域臺風浪最大波高與相應周期的長期聯合概率分布做實證分析，獲得如下結論：

（1）通過擇優選取了年最大波高H1/10與相應周期T的邊緣分布分別為P-III型分布和GEV分布，二者之間的較優連接函數為Archimedean類的Gumbel-Hougaard copula函數；

（2）同頻率條件下聯合分布重現水平設計值大于邊緣分布設計值，其中波高設計值的差異略大于周期設計值；同現重現期和聯合重現期的設計值可作為海岸海洋工程建設中的設計波高和相應周期的上下限，此有助于對工程資金投入與風險管理的綜合考慮；

（3）條件概率1表明，同頻率下的年最大波高和相應周期的遭遇概率介于70.4%～81.3%，此相對很高的組合概率可作為工程建筑物損毀風險率；條件概率2顯示，當設計波周期小于某定值時，年最大波高H1/10與相應平均周期T的遭遇概率明顯減小，同頻率下二者的遭遇概率小于20%。

Favre A C，AdlouniSE，Perrault L，etal，2004.Multivariate hydrological frequency analysis using Copulas.Water resources research，40（11）：1-12.

Genest C，Rivest L，1993.Statistical inference procedures for bivariate Archimedean copulas.Journal of American Statistical Association，88：1034-1043.

Joe H，1997.Multivariate Modelsand Dependence Concepts.Chapman&Hall，London.

OchiM K，1978.Wave statistics for the design of ships and ocean structures.SNAME Transactions，86：47-76.

Shiau J T，Song F，Nadarajah S，2007.Assessment of hydrological droughts for the Yellow River，China，using copulas.Hydrological Processes，21：2157-2163.

Wahl T，Mudersbach C，Jensen J，2012.Assessing the hydrodynamic boundary conditions for risk analyses in coastal areas：amultivariate statistical approach based on Copula functions Nat.Hazards Earth Syst.Sci.，12：495-510.

Zhang L，Singh V，2006.Bivariate Flood Frequency Analysis Using the CopulaMethod.J.Hydrol.Eng.，11（2）：150-164.

Zhang L，Singh V P，2007.Bivariate rainfall frequency distributions using Archimedean copulas.Journal of Hydrology，332：93-109.

陳子燊，劉曾美，2011.不同歷時設計暴雨組合的風險率分析.水文，31（4）：12-17.

陳子燊，2011.波高與風速聯合概率分布研究.海洋通報，30（2）：158-163.

方鐘圣，戴順孫，金承儀，1989.海洋特征波高和周期的長期聯合分布及其應用.海洋學報，11（5）：535-543.

劉曾美，陳子燊，2009.區間暴雨和外江洪水位遭遇組合的風險.水科學進展，20（5）：619-625.

馬桂芝，1988.重現期設計波高相對應的波浪周期推算方法的討論.海洋湖沼通報，4：87-90.

潘錦娥，1989.顯著（或有效）波高與平均周期的長期聯合分布探討.海洋通報，8（3）：1-10.

秦振江，孫廣華，閆同新，等，2007.基于Copula函數的聯合概率法在海洋工程中的應用.海洋預報，24（2）：83-90.

熊立華，郭生練，肖義，等，2005.Copula聯結函數在多變量水文頻率分析中的應用.武漢大學學報（工學版），38（6）：16-19.

趙耀南，1982.等重現期的最不利設計波浪.海洋學報，4（5）：754-762.