傳感器網絡中基于局部信號重建的目標計數算法

蔣文濤，孫利民，呂俊偉，朱紅松

（1. 海軍裝備研究院，北京 102249；2. 海軍航空工程學院 控制工程系，山東 煙臺 264001；3. 中國科學院 信息工程研究所，北京 100093）

1 引言

目標監測是傳感器網絡的重要應用領域之一[1]，例如敏感場所的防入侵告警系統、災后緊急搜救以及野生動物保護等。在單目標監測應用中，傳感器網絡只需要對區域內是否存在目標進行檢測；而在多目標監測應用中，傳感器網絡不僅要對目標是否存在進行檢測，還需要對目標的數量進行準確地統計，為用戶提供更全面的監測信息和決策依據。本文針對多目標監測應用中的目標計數問題展開研究。

傳感器網絡中目標計數的難點在于，節點通常只能被動地采集監測區域中的目標信號（例如紅外輻射強度、震動強度和聲音分貝值等），而不能區分測量值是來源于單個目標，還是由多個目標的信號疊加產生。雖然可以采用射頻標簽（RFID）技術[2]對目標進行識別和計數，但在一些應用場景中目標具有敵對性或者不可預知性，在這類目標上放置射頻標簽的可行性較低。除射頻標簽技術以外，指紋定位[3]也可用于目標計數，但創建指紋數據庫的工作量很大，并且易受環境變化的影響，當目標較密集或者聚集在一起時該方法的計數效果較差。其他方法，如超聲測距[4]、頻譜檢測[5]以及圖像識別[6]等，雖然也可以用于目標識別和計數，但對硬件基礎要求較高，難以適用于資源受限的傳感器網絡。

鑒于上述計數方法的局限性，研究人員提出了一些不需要特定硬件支持的目標計數算法，大致可以分為如下幾類：1）基于二元感知模型的計數算法[7,8]；2）基于分簇的計數算法[9,10]；3）基于壓縮感知理論的計數算法[11,12]；4）基于拓撲融合的計數算法[13,14]；5）其他類型的計數算法，例如Shuo Guo等[15]提出的基于概率模型的計數算法，Sorabh Gandhi等[16]提出的基于上下限估計的目標計數算法等。下面對一些有代表性的算法進行介紹和分析。

Jaspreet Singh等[7]研究了利用二元傳感器節點進行多目標計數和跟蹤的相關問題，證明了當一組目標中兩兩之間的距離都超過節點檢測半徑的4倍時，二元傳感器節點的計數準確性才能得到保證。文獻[9]提出了一種基于信號相關的目標計數算法，根據信號序列之間的相關性對節點進行分簇，將信號相關性較大的節點歸為一簇，并對應一個目標。該算法的實現較為簡單，但只適用于稀疏目標的計數，當目標較密集尤其是多個目標距離很近時，算法的計數準確性不高。Qing Fang等[10]提出了一種面向目標計數的輕量級感知和通信協議，包括DAM、EBAM和EMLAM 3種算法，基本思想是根據節點的測量值大小將網絡劃分為若干個簇，每個簇對應一個或多個目標。這3種算法的計數過程均需要網絡中所有節點同時參與，即使測量值很小的節點也不例外，因此算法的能量效率較低。Bowu Zhang等[12]提出了一種貪婪匹配追蹤（GMP，greedy matching pursuit) 算法，該算法是一種全局集中式計數算法，采用了壓縮感知理論[17]的相關模型來解決稀疏目標的計數問題，在網絡規模不大時具有很好的計數效果。GMP算法的不足之處是計數過程中將監測區域作為一個整體來對待，求解復雜度隨網絡規模增大呈指數狀增加。另外，GMP算法將監測區域劃分為若干個柵格，并以柵格中心代替目標的實際位置，沒有考慮柵格劃分粒度對計數精度和計算復雜度的影響。Shuo Guo等[15]專門針對目標計數中存在的重復計數問題展開了研究，假定每個節點能夠準確感知自己監測范圍內的目標數量，然后以此為基礎計算全網目標總數的概率密度函數，以目標總數的期望值作為計數結果。該目標計數算法的思路較為新穎，但前提條件過于苛刻，影響了算法的適用范圍。

本文借鑒信號重建[18]的相關理論，提出了一種基于局部信號重建的目標計數算法（LSR，target counting algorithm via local signal recovery）。LSR 算法的主要特點如下：1）該算法是一種局部集中式目標計數算法，計數過程只在有可能存在目標的局部區域內進行，不需要全網所有節點同時參與計數，能量效率較高；2）考慮了測量噪聲對信號重建的影響，并進行了優化設計，計數精度受噪聲影響較小；3）可以根據局部區域內的節點分布情況自適應地設定柵格劃分粒度，在計數精度和計數開銷之間進行權衡；4）針對計數過程中可能出現的外部干擾和重復計數問題，設計了相應的處理機制，算法具有較好的健壯性。

2 LSR算法設計

LSR算法的基本設計思路如下：1）通過局部峰值搜索找出目標可能存在的區域；2）對局部區域內的目標數量上限進行估算，并基于此約束條件建立信號重建模型；3）依據信號重建模型對目標分布進行估計，使得在某種分布估計下目標的信號場與節點實際測量值所反映的信號場最為逼近，將該分布估計下的目標數量作為局部計數結果；4）對各局部區域內的計數結果進行匯總，剔除計數重復的目標，得到整個監測區域的目標數量。

LSR算法通過被動測量目標發出的物理信號（紅外輻射、振動或聲響）來進行計數，不需要在目標上放置額外的硬件裝置。算法適用的網絡模型由以下幾條基本假設給出。

1) 所有傳感器節點的位置已知，并且具有相同的通信半徑R，所有節點的本地時間保持同步。

2) 傳感器節點的測量噪聲ξ為獨立同分布的白色高斯噪聲，即 ξ～N(0,σ2) 。

3) 目標移動速度相對較慢，短時間內監測區域內目標數量變化不大。為節省能量，網絡每間隔時間Δt執行一次目標計數算法。

4) 被監測目標為同一類目標，信號強度近似相同。

2.1 局部峰值搜索

設所有目標發出的信號強度均為I0，節點si和目標pj的距離為d( si, pj)，根據文獻[19]給出的信號測量模型，節點si測量值可以表示為

其中，λ為信號強度衰減因子，取值為2～5，c為參考距離。盡管文獻[19]未給出參考距離c的實際取值，但從信號連續性的角度考慮，c的值取為1較合理。由于式（1）沒有考慮信號疊加和噪聲問題，測量模型較為理想化，本文在其基礎上給出一個更完善的測量模型。設噪聲環境下節點si所處的區域內存在n個目標時，那么該節點的測量值可以表示為

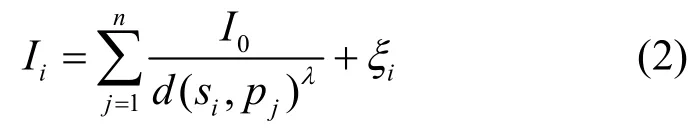
其中，ξi為節點si測量噪聲，當d( si, pj)＜1時，取d( si, pj)=1。

根據式（2）可知，目標的信號強度隨著傳輸距離的增大呈指數衰減，當傳輸距離增大到一定程度時，目標的信號強度與噪聲相當。因此，計數過程只需要在目標所處的局部區域內進行即可，不需要全網所有節點同時參與計數。為避免計數過程波及到不存在目標的區域，首先應進行局部峰值搜索，找出目標可能存在的局部區域。

定義1 峰值節點。若節點si的測量值比其一跳通信范圍內所有鄰居節點的測量值都高，那么稱節點si為峰值節點。

局部峰值搜索的目的是找出監測區域內的峰值節點，并以峰值節點為中心，組織其鄰居節點進行目標計數。一種可行的方法是根據節點的測量值大小設定一個定時器，定時器短的節點優先發送一個峰值消息，宣告自己為峰值節點，并對其他節點進行抑制。本文采用動態定時器策略來調節局部峰值搜索過程的收斂速度，其基本原理是：將時間劃分為長度為tw的窗口，若局部區域內存在測量值較大的節點，那么這些節點的定時器可以在前幾個窗口內快速截止；若前幾個窗口內沒有節點發送峰值通告消息，則表明局部區域內節點的測量值都較小，為減少等待時間，節點的定時器在后續窗口加速截止。按照上述策略設置的定時器為

其中，t0為網絡允許的最大等待時間；Ti( k)表示節點si在第k個窗口的剩余等待時間，其值隨著窗口數k的增加動態變化。若Ti( k)＜tw，則節點si的定時器在第k個窗口內截止。

當新一輪目標計數的執行時間到時后，任一節點si按下面的流程進行操作。

Step1 若節點si的測量值Ii超出給定的門限值Imin，則按式（3）設定一個時間長度為Ti( k)的定時器，參與峰值節點競爭。

Step2 若節點si的定時器截止前，收到某個鄰居節點sj發送的峰值通告消息（包含節點sj的ID號和測量值Ij），并且滿足Ii≤Ij，那么節點si判定該峰值通告消息有效，在信道空閑時將自己的測量值發送給節點sj。

Step3 若節點si的定時器在第k個窗口內截止，并且在此之前未收到有效的峰值消息，那么該節點向鄰居節點廣播自己的峰值消息，并在后續時刻接收鄰居節點反饋的測量值。

2.2 目標計數方法

局部區域內的目標計數分為如下幾個步驟：首先確定峰值節點一跳通信范圍內的目標數量上限，并在該約束條件下建立信號重建模型；然后以信號重建模型為基礎，尋求目標分布的最佳估計，將最佳分布估計對應的目標數量作為計數結果。

定義2 通信邊界圓周。節點si一跳通信范圍的邊界稱為節點si的通信邊界圓周，記為O(si)。

定義3 圓周對應點。設si為峰值節點，O(si)為si的通信邊界圓周，sj（j≠i）為si的一跳鄰居節點，從sj出發并且經過si的射線與O(si)的交點，稱為sj的圓周對應點，記為s′j。特殊地，定義峰值節點si的圓周對應點為O(si)上任意一點。

下面給出峰值節點一跳通信范圍內目標數量上限的估計方法。不失一般性，先以3個節點為例來進行分析，如圖1所示：si為峰值節點，sj和sk為si的一跳鄰居節點，sj′為sj的圓周對應點，sk′為sk的圓周對應點。

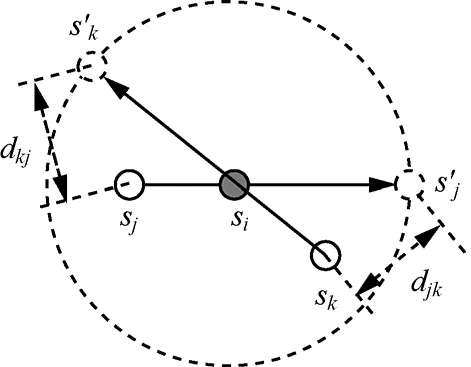
圖1 目標數量上限估計

對于節點sj而言，當目標位于s′j處時，信號到達節點sj時的衰減幅度最大。因此，當所有目標全部位于s′j處時，O(si)內的目標數量N才有可能取到最大值。另外，當多個目標位于s′j處時，在節點sk處的信號疊加值不應超過Ik，因此N的取值還應滿足條件。同理有，即：

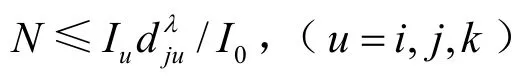
類似地，對于節點sk和si，也有如下關系成立：

推廣到一般情況，當O(si)內有n個節點時，目標數量N的上限Nmax可以表示為

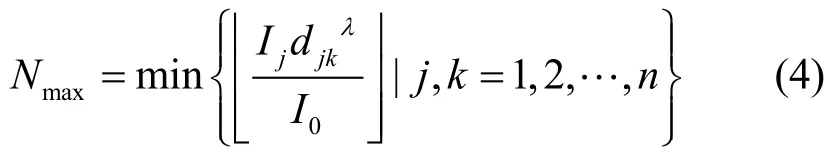
其中，Ij（j=1,2,…,n）表示節點sj的測量值，符號表示向下取整；當djk＜1時，取djk=1。

得到目標數量的上限Nmax后，就可以通過信號重建的方式，對O(si)之內的目標分布和數量進行估計。為方便計算，將O(si)的外接矩形近似作為峰值節點si的一跳通信范圍（如圖2所示），并將其劃分為l×l=m個柵格，每個柵格的邊長為a=2R/ l。對柵格按照從左至右，從上至下的順序進行編號，gi（i=1,2,…,m）表示第i個柵格。當柵格gi中存在一個目標時，該目標的信號對節點sj（j=1,2,…,n ）的測量值貢獻量為，其中，rij表示柵格gi的中心到節點sj的距離，rij＜1時，取rij=1。

類似地，可以得到m個柵格中的目標分別對n個節點的測量值貢獻量，用矩陣H表示為

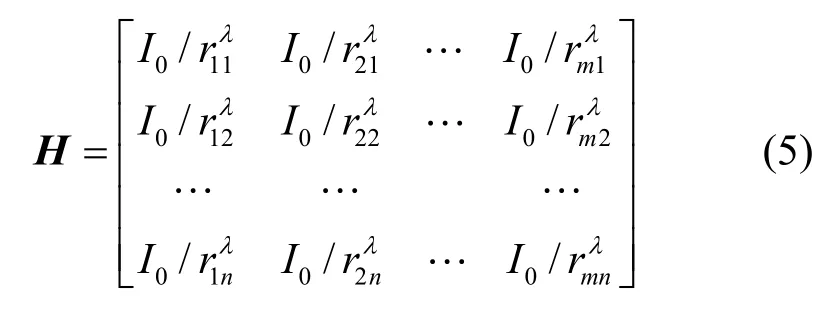
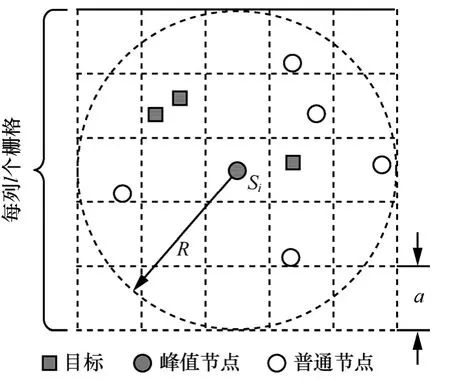
圖2 柵格劃分

設未知量xi表示柵格gi（i=1,2,…,m）中存在的目標數量，那么O(si)內的目標分布可用向量x=(x1, x2,…,xm)T來表示。記S={s1, s2,…,sn}中各節點的測量值構成的向量為y=(I1, I2,…,In)T，則局部區域內的信號重建模型可以表示為

其中，Z+表示正整數集。根據式（6）給出的信號重建模型，向量x的最佳估計可以表示為

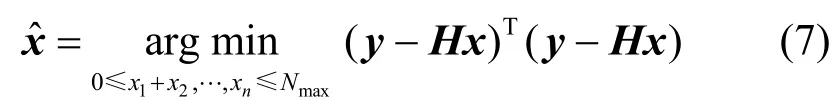
實際上，傳感器節點的測量值Ii（i=1,2,…,n）不可避免地會受到噪聲污染，并不能準確地反映節點si（i=1,2,…,n）所在位置的真實信號強度。假設x?為x的無偏估計，Ii′為節點si的理想測量值，ξi為節點si的測量噪聲，即ξi=Ii-Ii′，則有

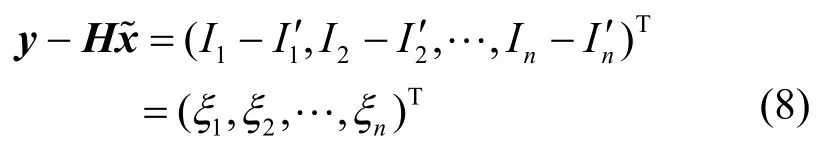
由于噪聲ξ為獨立同分布的白色高斯噪聲，并有ξ～N (0,σ2)，根據數學期望的性質可得：

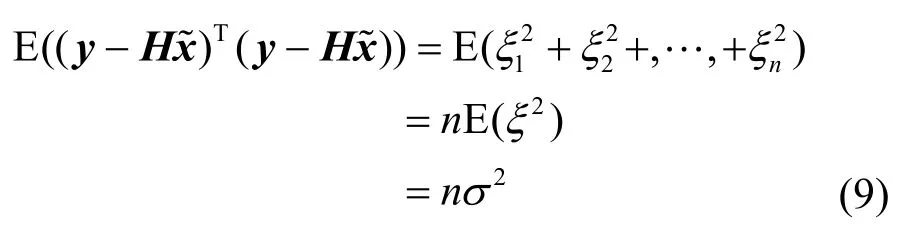
因此，在白色高斯噪聲環境下，向量x的最佳估計應修正為

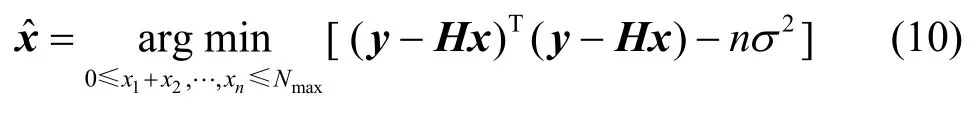
式（10）的求解可以采用匹配追蹤（MP，matching pursuit）[20]，正交匹配追蹤（OMP，orthogonal matching pursuit)[21]等算法來實現。得到=(x1, x2,…,xm)T的值后，O(si)內的目標數量可以表示為

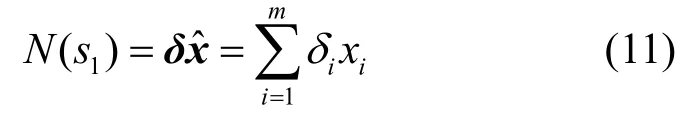
其中， δ=(δ1, δ2,…,δm)，式（11）的意義是當柵格中心處于O(si)之外的區域時，該柵格中的目標將從峰值節點si的計數結果中剔除。

2.3 柵格粒度優化設定

上一節的計算過程中，直接以柵格中心到節點的距離rij代替了目標與節點的實際距離，由此引入了一定的信號重建誤差。記r=-rij，那么信號重建誤差可以表示為

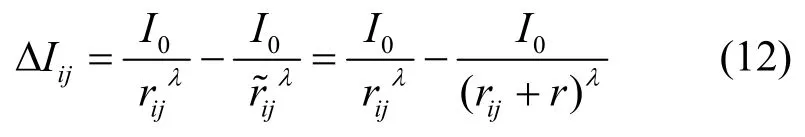
在無先驗信息的情況下，目標可能出現在任一柵格gi（i=1,2,…,m）中的任何一點，因此柵格gi中的目標到節點sj的距離是一個隨機量。若給定柵格邊長a的值，那么柵格劃分數量m及節點sj到柵格中心gi的距離rij（i=1,2,…,m ，j=1,2,…,n）也就隨之確定了。因此，信號重建誤差ΔIij是以隨機量和柵格邊長a為變量的函數。若用的期望值E()來代替，則有

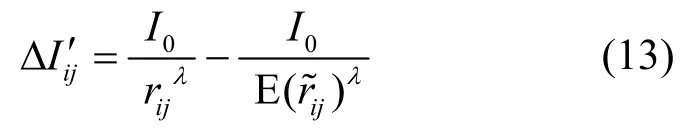
為了提高信號重建的精度，柵格邊長a的取值應使 ΔIi′j（i=1,2,…,m ，j=1,2,…,n ）的累加值盡可能小。當a→0時必有ΔIi′j→0，此時ΔIi′j的累加值可以達到最小。然而，目標分布估計的計算復雜度是隨著柵格劃分數量m的增加而增加的，當a→0時m=(2R/ a)2→+∞，這是資源受限的傳感器網絡難以承受的。若在信號重建誤差和計算開銷之間進行權衡，則可以得到

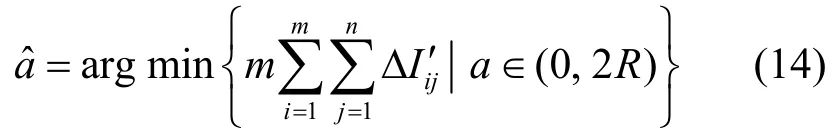
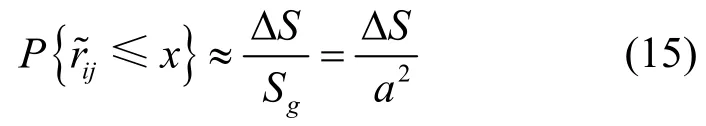
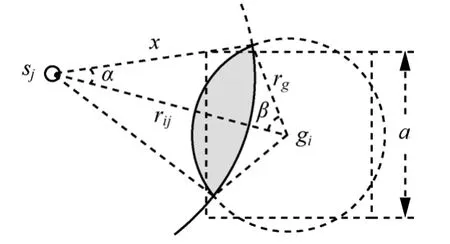
圖3 的期望值計算

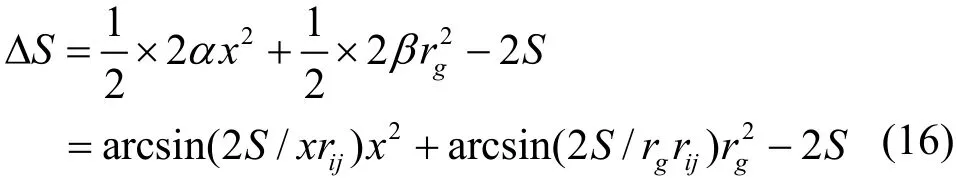
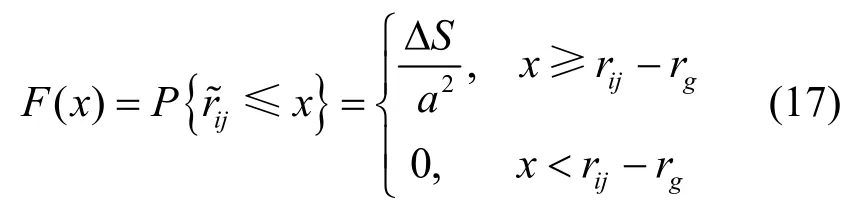
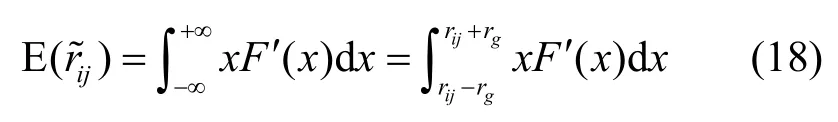
式（18）涉及到微積分運算，計算復雜度較高，下面給出一種近似計算方法。令（k=0,1,…,z），則有

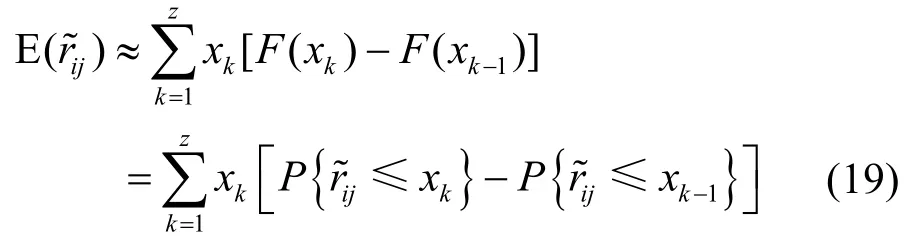
2.4 外部干擾排除

2.2節中的目標計數是一種較理想的情況，僅適用于O(si)之外的鄰近區域不存在目標的情況。若O(si)之外的鄰近區域存在目標，那么靠近O(si)的節點會受到較強的外部干擾。為保證計數結果的準確性，信號重建過程中需要排除集合S={s1, s2,…,sn}中靠近O(si)的節點。如圖4所示，陰影區域為受限區域，處于該區域中的節點不能參與計數，其中R為O(si)的半徑，R′為非受限區域的半徑，并有τ=R-R′，下面給出τ的取值設定方法。

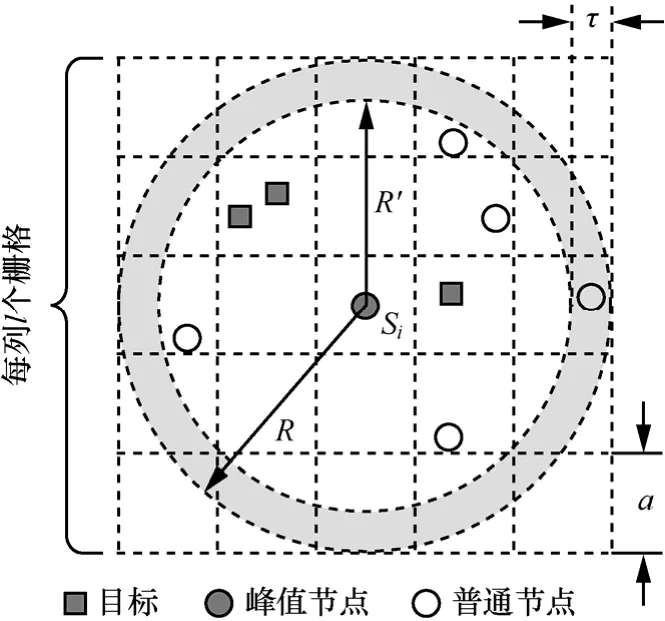
圖4 干擾排除

由于傳感器節點的測量噪聲ξ為獨立同分布的白色高斯噪聲，并有ξ～N(0,σ2)，根據3-σ準則可知P{-3σ＜ξ＜3σ}=0.997，因此測量噪聲ξ的最大值可取為ξmax=3σ。顯然，τ的取值應使O(si)之外的目標發出的信號經過距離為τ的衰減后，信號強度衰減到與測量噪聲相當的水平，即，由此可得

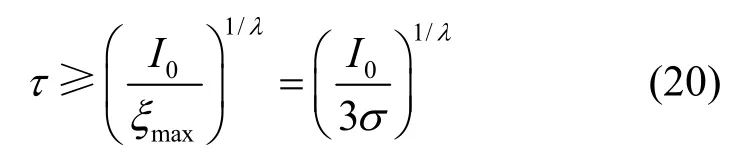
然而在弱噪聲環境下，噪聲均方差σ的值可能較小，依據式（20）得到的τ值較大，致使O(si)之內過多的傳感器節點受到限制。為應對這種情況，τ的取值還應受到其他限制。假設O(si)之外的目標發出的信號經過距離為τ的傳播后，信號強度與初始信號強度的衰減比為ε。如果ε的值足夠小，那么O(si)之外的目標對非受限區域內節點的影響可以忽略不計，此時對應的τ值即為所求。令，則有

結合式（20）和式（21），τ的臨界取值可以表示為

2.5 全網目標計數

設網絡監測區域內存在h個峰值節點，各峰值節點的計數結果分別為N( si)（i=1,2,…,h），那么監測區域內的目標總數可以表示為

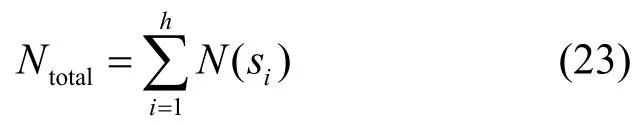
然而在目標較密集的情況下，有可能產生重復計數問題。如圖5所示，s1、s2和s3為峰值節點，目標p1處于O(s1)、O(s2)和O(s3)的交疊區域內，若按式（23）進行目標數量匯總，目標p1將被重復統計3次。

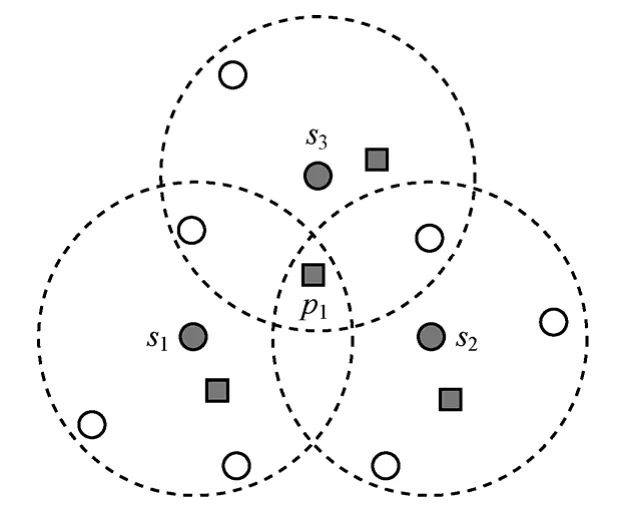
圖5 重復計數

針對可能發生的重復計數問題，本文采用單向排除策略來修正各峰值節點的計數結果，具體方法如下。

1) 單向排除策略從任一峰值節點si開始執行，該節點首先檢查自己的通信邊界圓周O(si)是否與其他峰值節點的通信邊界圓周交疊。若結果為“否”，那么節點si停止其他操作。

2) 若節點si的通信邊界圓周與一個或者多個峰值節點的通信邊界圓周發生交疊，那么si向對應的峰值節點發送出計數重復通告消息（包含交疊區域內的目標數量及其所處的柵格位置），令對方節點從計數結果中刪除與自己重復的目標。

3) 若節點si已經向某個峰值節點發送了計數重復通告消息，那么對方節點無需再向節點si發送計數重復通告消息。當所有峰值節點都執行完上述操作流程后，單向排除過程自動結束。

執行完單向排除策略后，各峰值節點將自己的計數結果修正為N′( si)(i=1,2,…,h )，并上報給Sink節點，Sink節點匯總各峰值節點的上報數據后即得到監測區域內的目標總數：

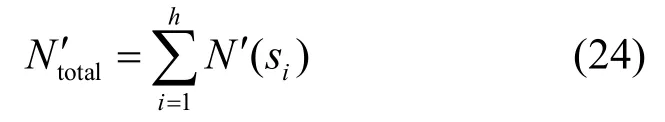
3 性能測試

3.1 參數設置

本文采用Omnet++（Version 4.1）和Matlab 7.0來對LSR算法的性能進行仿真測試實驗。實驗場景如下：紅外傳感器節點隨機均勻部署在500m×500m的區域內，數量為100～400；目標（人）數量為10～50，以較低的速度在監測區域內活動。LSR算法每間隔60s執行一次，傳感器節點通過測量目標的紅外輻射強度來進行目標計數。由于目標離傳感器節點的距離較近，實驗中不考慮大氣消光系數對目標紅外輻射強度的影響。

為了驗證LSR算法的性能，仿真實驗以EBAM算法[10]和GMP 算法[12]為參照對象，在相同網絡環境下對3種算法的計數精度和通信開銷進行測試。實驗中LSR算法的柵格邊長根據式（14）的計算結果自動設定。由于GMP 算法的計數過程中也采用了柵格劃分的方法，但未給出柵格邊長的取值，為便于比較，GMP 算法的柵格邊長與LSR算法的柵格邊長取值相同。計數精度以相對計數誤差（計數誤差的絕對值與實際目標數量的比值）來衡量；通信開銷以計數過程中的數據發送量（字節數）來衡量。為消除小概率事件的影響，所有實驗結果以20次仿真的平均值來表示。其他仿真參數的設置如表1所示。

表1 主要仿真參數設置

3.2 測試結果與分析

圖6給出了3種算法在不同目標密度下的計數精度測試結果，節點數量為300，噪聲均方差σ=3，目標數量在10～50之間變化。從圖6可以看出，EBAM算法的計數精度受目標密度變化的影響較大，而LSR算法和GMP算法的計數精度穩定在10%以內。上述情況與3種算法的計數方法不同有較大關系。由于EBAM算法是一種基于分簇的計數算法，目標密度越大則每一簇內分布的目標數量也越多，出現計數偏差的可能性也就越大。而LSR算法和GMP算法的計數精度主要取決于測量信息的豐富程度，在節點數量不變的情況下，計數精度較為穩定。

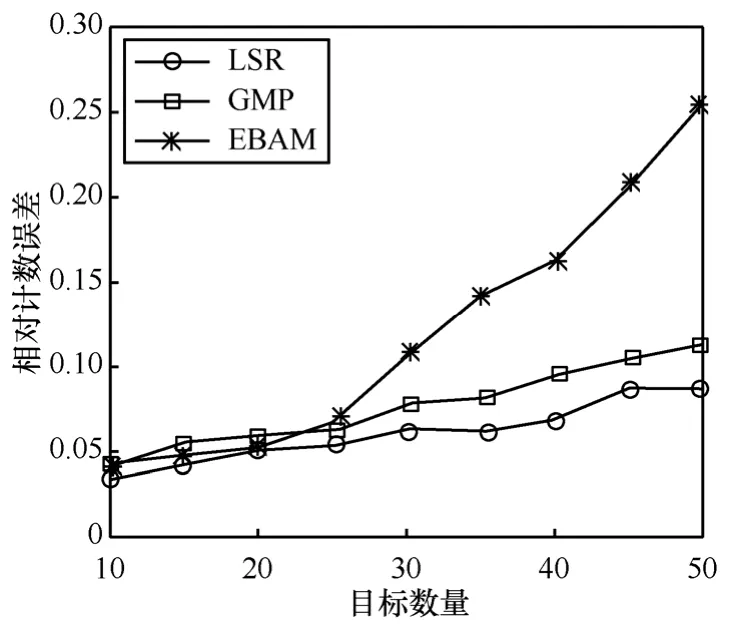
圖6 目標密度對計數精度的影響

圖7是3種算法在不同節點密度下的計數精度測試結果，目標數量為30，噪聲均方差σ=3，節點數量在100～400之間變化。從圖7可以看出，LSR算法和GMP算法對節點密度的變化較為敏感，相對計數誤差隨節點密度變化的波動幅度較大。原因是節點密度越大，測量信息越豐富，信號重建和計數的準確性也就越高，反之亦反。而在監測區域內目標數量不變的情況下，EBAM算法每一簇內分布的目標數量相差不大，因此計數精度只在5%～12%內小幅度變化。

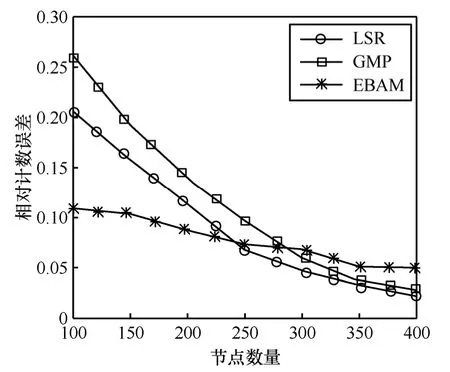
圖7 節點密度對計數精度的影響

圖8是3種算法在不同噪聲水平下的計數精度測試結果，節點數量為300，目標數量為30，噪聲均方差在1～5之間變化。從圖中可以看出LSR算法和 EBAM 算法的相對計數誤差穩定在10%以內，而GMP算法在噪聲均方差較大的情況下，相對計數誤差達到20%左右。這是由于LSR算法和EBAM算法針對噪聲的影響分別進行了優化設計和平滑過濾，而GMP算法雖然在仿真實驗中考慮到噪聲的影響，但并沒有設計具體的噪聲抑制策略，故抗噪性比前2種算法要差。

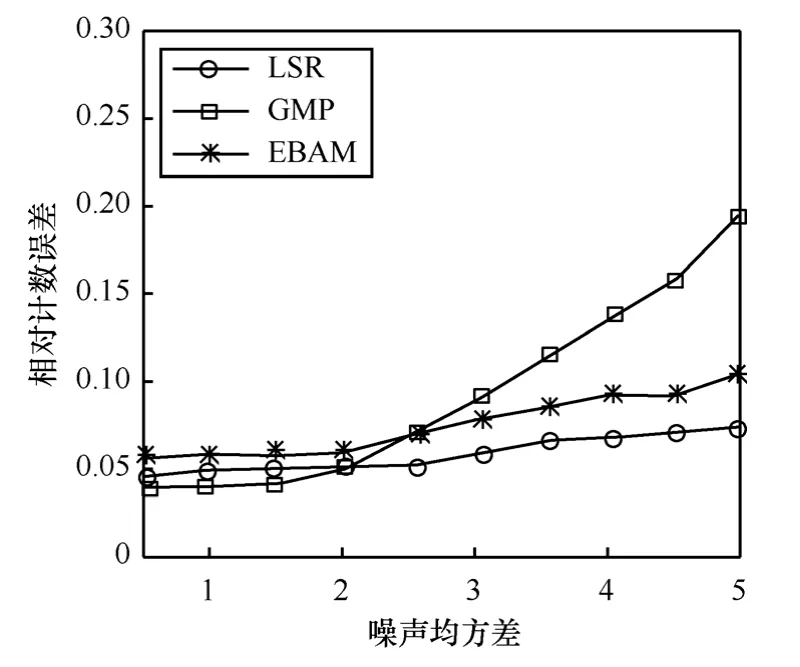
圖8 噪聲對計數精度的影響

前面的仿真實驗在網絡規模一定的情況下對 3種算法的計數精度進行了測試，下面將在不同網絡規模下對3種計數算法的計數開銷進行仿真測試。網絡規模以 500m×500m為單位面積，節點分布密度為每單位面積300個，目標分布密度為每單位面積30個，噪聲均方差σ=3。

圖9是3種算法在網絡規模分別為1～4個單位面積下的通信開銷測試結果。EBAM算法計數過程中需要在全網范圍內進行分簇操作，由此產生大量的報文消息，因此算法的總體數據發送量較大。而LSR算法是一種局部集中式計數算法，計數過程只在可能存在目標的局部區域內進行，因此總體數據發送量相對較小。GMP算法是一種集中式計數算法，各節點只需將自己的測量值發送給中心節點，無需額外的控制開銷，網絡規模較小時的數據發送量較少；但隨著網絡規模的擴大，測量節點到中心節點的跳數增多，每個節點的測量值都需要經過更多跳數的轉發才能到達中心節點，故通信開銷大幅上升。

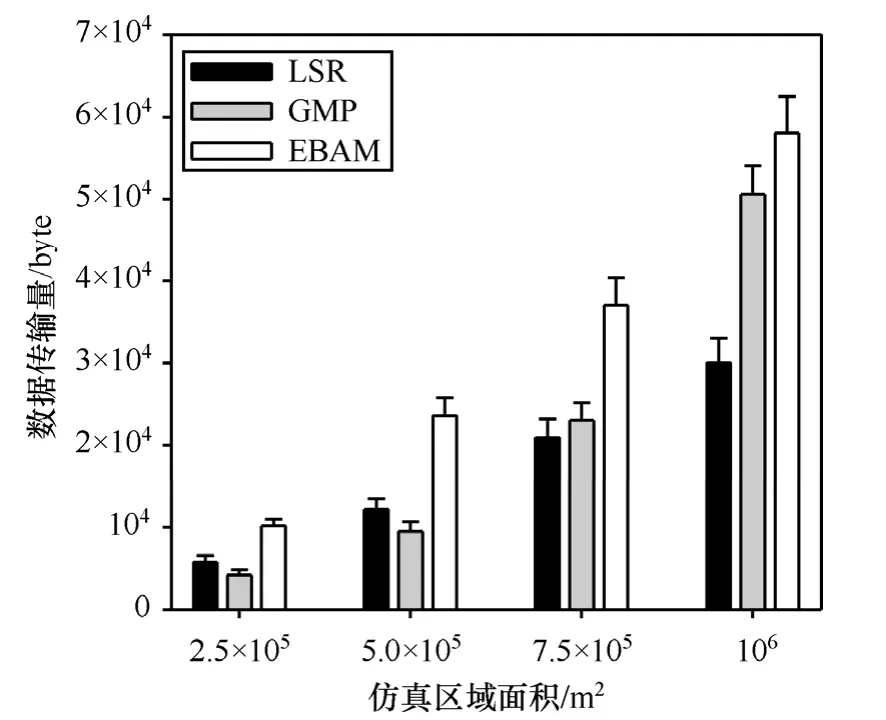
圖9 算法通信開銷比較

4 結束語

目標計數是傳感器網絡在多目標監測應用中需要實現的基本功能，也是其面臨的技術難點之一。針對現有目標計數算法在計數精度、能量效率等方面的不足，本文設計了一種基于局部信號重建的目標計數算法LSR。該方法不需要在目標上放置額外的硬件裝置，僅通過被動測量目標自身發出的信號來計數，硬件復雜度較低。LSR算法是一種局部集中式計數算法，計數過程只在某些可能存在目標的局部區域內進行，無需全網所有節點同時參與計數，因此可以大幅度降低計數過程的能量開銷。LSR算法的應用場景是目標的信號強度近似相等且已知，具有一定的局限性，下一步將研究設計目標信號強度不同條件下的目標計數算法。

[1] 李建中, 高宏. 無線傳感器網絡的研究進展[J]. 計算機研究與發展,2008, 45 (1): 1-15.LI J Z, GAO H. Survey on sensor network research[J]. Journal of Computer Research and Development, 2008, 45(1): 1-15.

[2] 李敏波, 全祖旭, 陳晨. 射頻識別在物品跟蹤與追溯系統中的應用[J].計算機集成制造系統, 2010, 16(1): 202-208.LI M B, JIN Z X, CHEN C. Application of RFID on products tracking and tracing system[J]. Computer Integrated Manufacturing Systems,2010, 16(1): 202-208.

[3] KAEMARUNGSI K, KRISHNAMURTHY P. Modeling of indoor positioning systems based on location fingerprinting[A]. INFOCOM 2004[C]. 2004.1012-1022.

[4] 彭剛, 黃心漢, 王敏. 基于視覺引導和超聲測距的運動目標跟蹤和抓取[J]. 高技術通訊, 2002, 12(6): 74-79.PENG G，HUANG X H, WANG M. Moving object tracking and grasping based on visual guiding and ultrasonic measurement[J]. High Technology Letters, 2002, 12(6): 74-79.

[5] 吳海彬. 聲磁傳感器及其頻譜檢測技術研究[J]. 儀器儀表學報,2008,29(5): 1100-1104.WU H B. Research of acoustomagnetic sensor and its frequency spectrum detection technology[J]. Chinese Journal of Scientific Instrument,2008, 29(5): 1100-1104.

[6] 趙文哲, 秦世引. 基于感興趣點特征的彩色圖像目標分類與識別[J]. 系統工程與電子技術, 2011,33(2): 438-442.ZHAO W Z, QIN S Y. Chromatic image classification and recognition based on interest point features[J]. Systems Engineering and Electronics, 2011, 33(2): 438-442.

[7] JASPREET S, UPAMANYU M, RAJESH K. Tracking multiple targets using binary proximity sensors[A]. IPSN 2007[C]. Cambridge,Massachusetts, USA, 2007. 529-538.

[8] SHRIVASTAVA N, MUDUMBAI R, MADHOW U. Target tracking with binary proximity sensors[J]. ACM Transactions on Sensor Networks, 2009, 5(4): 1-33.

[9] 陶良鵬. 無線傳感器網絡中基于信號相關的目標計數[D]. 合肥:中國科學技術大學, 2008.TAO L P. Signal Correlation Based Target Counting in Wireless Sensor Networks[D]. Hefei: University of Science and Technology of China, 2008.

[10] FANG Q, ZHAO F, GUIBAS L. Lightweight sensing and communication protocols for target enumeration and aggregation[A]. MobiHoc 2003[C]. Annapolis, Maryland, USA, 2003. 165-176.

[11] MENG J, LI H, HAN Z. Sparse event detection in wireless sensor networks using compressive sensing[A]. The 43rd Annual Conference on Information Sciences and Systems (CISS)[C]. Baltimore, Maryland,USA, 2009. 181-185.

[12] ZHANG B W, CHENG X Z, ZHANG N. Sparse target counting and localization in sensor networks based on compressive sensing[A].INFOCOM 2011[C]. Shanghai, China, 2011. 2255-2263.

[13] BARYSHNIKOV Y, GHRIST R. Target enumeration via integration over planar sensor networks[A]. Robotics Science and Systems Conference[C]. Zurich, Switzerland, 2008. 1-9.

[14] BARYSHNIKOV Y, GHRIST R. Target enumeration via euler characteristic integrals[J]. SIAM Journal on Applied Mathematics, 2009,70(3): 825-844.

[15] SHUO G, TIAN H, MOHAMED F M. On accurate and efficient statistical counting in sensor-based surveillance systems[J]. IEEE Pervasive and Mobile Computing, 2010, 6(1): 74-92.

[16] SORABH G, RAJESH K, SUBHASH S. Target counting under minimal sensing: complexity and approximations[A]. ALGOSENSORS 2008[C]. Reykjavik, Iceland, 2008. 30-42.

[17] CANDS E, WAKIN M. An introduction to compressive sampling[J].IEEE Signal Processing Magazine, 2008, 25(2): 21-30.

[18] NEEDELL D, TROPP J A. Cosamp: iterative signal recovery from incomplete and inaccurate samples[J]. Applied and Computational Harmonic Analysis, 2008, 26(3): 301-321.

[19] CHIN T L, RAMANATHAN P, SALUJA K K. Exposure for collaborative detection using mobile sensor networks[A]. MASS 2005[C].Washington D C, USA, 2005. 743-750.

[20] TROPP J A. Greed is good: algorithmic results for sparse approximation[J]. IEEE Transactions on Information Theory, 2004, 50(10):2231-2242.

[21] TROPP J A, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53 (12): 4655 -4666.