基于離散變量自適應遺傳算法的改進

呂秀芹

（江蘇農林職業技術學院，江蘇句容 212400）

遺傳算法(Genetic Algorithm，GA)是一種基于模擬自然界生物遺傳演化規律的隨機探索和優化算法[1]。算法將問題對象進行編碼，形成類似生物學上的染色體，通過對染色體的遺傳進化，從而得到問題的優化解。算法能有效地處理大量離散參數，在求解之初可以采取一些方法使得初始種群在解空間合理分散，并且通過基因交叉和變異操作，增加了全局尋優的能力。遺傳算法目前已廣泛地應用于函數優化、組合優化、自動控制、圖像處理、生產調度等多個行業。

算法的基本運算過程[2]為：將問題對象以二進制或實數等形式進行編碼，把問題的單個可行解看成是一個符號串，從而形成類似生物學上的染色體或個體。然后隨機生成M個個體作為初始群體P(0)，用已設計好的適應度函數計算當前群體中每個染色體的適應度值，系統根據問題域中個體的適應度大小選擇新的染色體，使用選擇算子將適應度高的染色體選擇進入下一代，然后再利用這些已選擇的染色體進行交叉、變異等操作，產生出代表新的解集的群體P(t)。上述生成新群體P(t)的過程不斷重復，直到找到問題的解滿足用戶的要求為止。由于交叉、變異后產生的新種群與其父種群相比，更能適應于環境，當算法結束后，將末代種群中包含的最優個體進行解碼即可得到問題的較優解。

遺傳算法通過計算比較個體染色體的適應度與群體平均適應度決定該個體進化或淘汰，但進化到了后期，算法搜索到最優解附近時，要確定最優解要花費大量時間，甚至無法精確定位最優解的位置，且算法容易出現“早熟”。針對算法的這些缺點，有不少學者在遺傳算子的改進方面做了不少研究并取得了豐碩的成果，引入了自適應策略改善遺傳的性能。

1 自適應遺傳算法

遺傳算法中遺傳算子影響進化的進行，其中交叉概率Pc和變異概率Pm對種群的優化起著決定性的作用。交叉概率和變異概率大，則新個體產生的速度快，有利于保持種群的多樣性，但過大又會使優選出的個體被壞，不利于選擇算子的作用。交叉概率和變異概率過小，容易產生局部收斂，算法出現早熟。遺傳算法按照優勝劣汰的規則,將適應度較高的個體更多地遺傳到下一代，算法使得種群后期的適應度要高于初期的適應度。Srinvivas等提出根據種群進化程度自適應遺傳算法的策略，即算法根據種群的適應度動態調整交叉概率Pc和變異概率Pm，具體見公式1和公式2。算法的基本思想是：對于適應度高于群體平均適應度的個體，取較小的交叉概率Pc和變異概率Pm，使得該解得以保護進入下一代；對于適應度低于群體平均適應度的個體，取較大的交叉概率Pc和變異概率Pm，使該解被淘汰[2]。

其中fmax為群體中最大的適應度值；fave為群體的平均適應值；f′為要交叉的兩個個體中較大的適應度值；f為要變異個體的適應度值；k1，k2，k3，k4取值在[0，1]區間，根據不同的問題特征，可根據實驗或經驗確定其值的大小。

可以看出，當個體的適應度值大于平均適應度值時，交叉概率Pc和變異概率Pm隨著個體的適應度增大呈線性遞減。當適應度越接近最大適應度時，即當前解越接近最優解，交叉概率和變異概率越小；當個體的適應度值接近或等于最大適應度值時，交叉概率和變異概率接近或等于零，算法停止收斂操作，將當前個體作為最優解[3]。上述的自適應過程在算法執行到后期有很好的收斂效果，但在算法運行的初期，由于此時的種群可能集中在解集的某個區域，優良個體可能是某一個區域的相對優解，而不是全局的最優解。因此，上述的自適應算法在進化初期容易產生局部收斂，產生“早熟”。

2 自適應遺傳算法的改進

在進化初期，為了保持種群的多樣性，應增加種群的交叉和變異操作。隨著遺傳算法進化過程的進行，群體中適應度較低的一些個體被逐漸淘汰掉，而適應度較高的一些個體會越來越多，種群已經接近最優解。為了使種群的一些好的特性不被破壞，此時的交叉和變異操作應降低。在進化后期，個體間的相似度增加，容易過早的收斂，此時應適當增加變異概率[4]。對于離散變量，初始種群一般以一定的方法盡量分散在解集中，其離散程度較大，進化若干代后，新的個體已經接近最優解，其離散程度明顯減小。本文設計根據個體的離散程度來送別其進化的程度，從而得到不同的遺傳概率。

考慮到種群在不斷的進化，交叉和變異操作不能盲目進行，相互之間應配合進行。本文對上述的自適應過程進行人工干預，引入兩個概率系數c和m分別影響交叉概率和變異概率的取值，從而有效防止其在進化初期陷入局部尋優，具體見公式(3)和公式(4)。

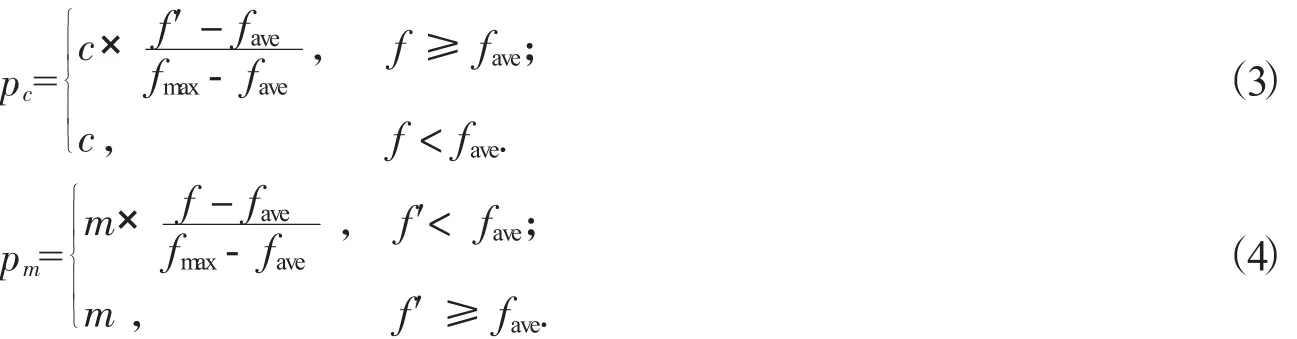
其中c，m為分別為交叉概率系數和遺傳概率系數，且c≤1，m≤1，其余參數含義同上。

隨著迭代進化的進行，每一代種群中個體適應度值的差異是不同的，概率系數c和m隨著進化的進行而變化的。在進化初期，種群的個體差異大，各染色體之間的適應度差別也較大，為了增加種群的多樣性，實現全局收斂性，此時c和m均取較大值，即交叉概率和變異概率取較大值，以加快進化的速度。隨著進化的發展，此時的解已經接近取優解的雛形，為了保讓優質個體被選擇復制到下一代遺傳，c和m的取值均應適當降低。到了進化的后期，種群中個體的適應度差別變小，交叉概率進一步變小，進化速度變慢，易陷入局部最優，此時應適當增加變異操作，避免進入種群“早熟”。

給概率系數c和m取值前，首先要判斷種群的進化程度，本文根據種群的離散程度系數Df和平均適應度與最優適應度之間的差值系數Dv進行衡量。離散程度以種群中個體的適應度的均方差表示，具體見公式(5)和公式(6)。

其中，Df為離散程度系數，Dv為平均適應度與最優適應度之間的差值；N為種群規模，ffit為系統設置的目標最優適應度，fi為種群中個體的適應度值。Df反映的是當前種群中個體間適應度的相似程度的大小。在進化初期，個體間離散大，其適應度值差異大，Df和Dv的值較大。進化到后期，個體接近最優解，種群中個體的相似度增大，Df和Dv的值較小。具體操作時，綜合這兩個系數衡量種群進化程度，引入進化程度系數D，令D=Df+Dv。通過比較D與第一代種群進化系數Df1的關系，從而得到當前種群的進化程度，以決定概率系數c和m的值，函數公式如下：

由于進化過程不斷進行，在進化初期，種群的進化程度系數接近Df1；；到最化后期，個體接近最優解，故進化系數接近0，故上面的公式中進化系數D在(0,Df1)間取值。對于不同特征的問題，c和m的值會有變化，本文以典型的離散問題——組卷問題為例，給出c和m的分段取值。可以看出，函數依據進化系數判斷進化的程度，從而決定概率系數c和m的不同取值，得到不同進化時期的交叉概率和變異概率，可以很好地控制進化過程，提高算法的性能。

3 算法性能驗證

為了驗證算法經過改進后其執行的效率和效果，本文應用改進前后的算法進行組卷試驗。試驗題庫包括600道題目，其中單選題300道，多選題100道，判斷題200道，按各種題型采用分段實數編碼的方案，設定知識點覆蓋率、難度系數、各題型題量等要求。使用Visual Studio.net提供的C#語言進行編程設計，程序在Xeon E5506 2.13GHZ，4GBDDR3，WindowServer2003環境下執行。通過設定不同的初始種群規模和最大迭代次進行組卷試驗，結果表明，算法經改進后在不同的遺傳代數其最優個體的適應度明顯高于改進前，提高了組卷成功率，降低了組卷時間。

4 結論

本文基于遺傳算法進化的特征，結合自適應遺傳算法提出的自動調整交叉概率和遺傳概率的理念，提出判斷每代個體的進化程度的方法，設計根據進化程度賦予個體的不同的交叉概率系數和遺傳概率系數，從而得到不同進化時期的交叉概率和遺傳概率，對個體的遺傳進行進化，實現算法的快速收斂，并避免了“早熟”現象。將算法用于處理典型的離散問題——組卷問題，算法性能有了較大的提高，其收斂速度明顯加快，組卷的成功率也有了提高。

[1]陳曉東,王宏宇.一種基于改進遺傳算法的組卷算法[J].哈爾濱工業大學學報,2005(9):1174-1175.

[2]張京釗,江濤.改進的自適應遺傳算法[J].計算機工程與應用,2010(46):54.

[3]張國強,彭曉明.自適應遺傳算法的改進與實現[J].船舶電子工程,2010(1):83-84.

[4]盧長娜,王如云,陳耀登.自適應遺傳算法[J].計算機仿真,2006(1):172-175.