GPC算法在火炮隨動系統中的仿真研究

霍 刊，王忠慶，楊執中，姜華杰

（中北大學 信息與通信工程學院， 山西太原 030051）

0 引言

由于在戰爭中對火炮應用需求的不斷提高，火炮隨動系統對快速性和準確性有越來越高的要求。這就是要求設計的自適應控制率，不僅需要強的魯棒性，而且算法的收斂速度要快，才能滿足系統的實戰要求。

近年來，隨著計算機運算速度的加快和數字化技術的廣泛應用，以及制造加工行業的技術更新的改進，從軟硬件兩個方面為把自適應控制引入火炮隨動控制奠定了基礎。基于不同的思路（如優化算法、系統辨識、預測控制等）的自適應控制相關研究迅速開展，目前研究的熱點是如何把自適應控制與智能控制結合起來，達到更好的控制效果的方法[1-2]。

1 GPC仿真

GPC方針是基于CARIMA模型的自校正控制策略，且在其推導過程中用到了系統辨識、多步預測、滾動優化等方法，包含了自適應控制的許多優點。故而，多年前人們已開始研究如何將其用于火炮隨動控制系統中。參考文獻[3]提出了一種針對交磁擴大機——直流電動機模型提出的非線性廣義預測控制(NGPC)算法，并對火炮隨動系統受到射擊干擾為4密位5步采樣寬度的方波干擾的情況下，通過仿真研究證明了該方法對沖擊干擾具有良好的抑制能力。本文主要研究該算法對火炮的齒隙非線性和外界不確定性干擾的控制性能即魯棒性。

CARIMA模型可以用于存在非平穩隨機擾動的情況，ξ(t)為不相關隨機序列，模型為：

它的擾動僅受當前狀態的影響。

GPC算法采用的是CARIMA模型和擴展預測控制的思想。具體地說，GPC控制的目標函數：

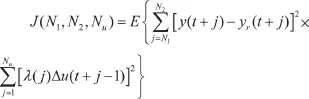
為了使GPC算法在多輸入多輸出(MIMO)系統應用中更加方便的調控，可在算法中引入Q、R兩變量，采用：

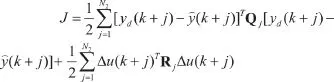
作為控制的目標函數。式中的Q、R為對角陣。并根據系統的狀態方程和輸出方程設計GPC算法，就可以完成在MIMO情況下的控制算法設計。按照這一方法對CARIMA模型進行仿真研究，將轉速控制率與轉速比環節合成后的傳遞函數，作為控制對象，設系統的齒隙非線性和不確定性的隨機干擾，并在6 s末，受到某階躍信號的干擾，取齒隙值為3，設采樣周期為10 ms，取N2=4，Nu=1，R=0.03I，Q=100I（I為單位陣），其仿真結構如圖1。可得到如圖2的仿真結果。表明GPC控制對齒隙非線性和不確定性干擾具有一定的魯棒性，可以應用于火炮隨動系統控制中[3-4]。

GPC算法雖然具有很好的控制性能，但是這種方法所用到的參數較多，許多參數仍需要反復調試，比如加權因子λ（或R矩陣）的選擇，就比較困難。下面給出一些簡單的參數選擇方法5。

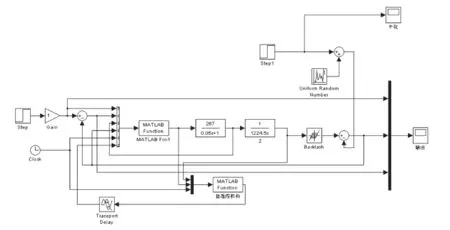
圖1 GPC仿真圖

圖2 GPC仿真結果

控制加權因子λ（或R矩陣），對快速性要求較高時應取較小的值，而對精度要求較高時應采取較大值當采樣周期較大時，小的λ值會引起大的誤差，控制精度降低，甚至引起大幅的極限環振蕩；當采樣周期較小時，控制精度大幅提高，即使存在振蕩也常在誤范圍之內，但受運算速度和分辨率的限制。N1的選擇：目前常選則N1=l； N2的選擇：由于目標函數中含有未來的控制，輸出長度應考慮包括受當前影響較大的所有相應段，所以N2應至少大于或等于na，nb中的較大者。 Nu的選擇：一般選Nu。=l，可以避免計算中出現逆陣。若不能達到再選擇更大值[6-8]。

2 結論

這里討論的只是一般的參數選擇規律，具體應該如何選擇要看實際控制系統的具體要求。從以上分析可以看出，GPC控制算法對系統的非線性、不確定感染有很強的抗擾性，從而具有良好的動態特性、高的控制精度和較強的魯棒性。然而，該方法計算復雜，許多參數如（N1、N1、λ）仍需要選擇，控制率設計相對繁瑣，所以可以適用于火炮隨動系統等控制性能要求很高的場合。

[1]楊益群,項國波.新的ITAE最佳傳遞函數標準型[J].信息與控制,1997,2(2):259-265.

[2]王正林,劉明.精通MATLAB7[M].北京:電子工業出版社,2007.

[3]高元樓.火炮機電伺服系統定位精度的研究[D].西安:西安交通大學,1999.

[4]中國兵器工業第202研究所.自行高炮隨動系統技術資料[Z].陜西咸陽.

[5]王正林,王勝開,陳國順,等.MATLAB/Simulink與控制系統仿真[M].2版.北京:電子工業出版社,2008:216-223.

[6]朱新華.自行高炮全炮控制電氣系統[M].石家莊:軍械工程學院出版社,1999:55-56.

[7]林飛,杜欣.電力電子應用技術的MATLAB仿真[M].北京:中國電力出版社,2009:1-296.

[8]劉金琨.先進PID控制及其MATLAB仿真[M].北京:電子工業社出版社,2003:271-272.