凸約束廣義線性模型參數(shù)MLE估計的收斂性研究
鐘紹軍,童恒慶
(1.咸寧學院 數(shù)學與統(tǒng)計學院,湖北 咸寧 437100;2.武漢理工大學 數(shù)學與統(tǒng)計學院,武漢 430070)
1 凸約束廣義線性回歸模型及其參數(shù)估計
考慮以下的評估工作:假定有m個被評估對象,有p個評估指標,對每一個評估對象的每一個指標,都有n個專家進行評估打分。p個指標分別以x(1),…x(p)表示。第i(i=1,…,n)個專家對第k(k=1,…,m)個對象的第j(j=1,…p)個指標進行評估,得到的分數(shù)記為xijk,每個專家對每個對象的評估分數(shù)是一個p維向量數(shù)據(jù),作為評估數(shù)據(jù)表的一行。顯然,每個對象的評估數(shù)據(jù)有n行,構(gòu)成一個數(shù)據(jù)塊。m個數(shù)據(jù)塊構(gòu)成一個立體數(shù)據(jù)陣X={xijk}。給每個評估對象最終的評估分數(shù)只有一個,記為yk(k=1,…,m),它也是待定的。評估模型可表述為

其中Dmn×n=Im?In,?是Kronecher積。這是童恒慶教授(1993)針對評估過程提出的一種特殊的凸約束廣義線性回歸模型[1]。童教授給出了模型參數(shù)的基于交互投影的最小二乘估計和基于EM算法的極大似然估計[2~4]。前者的收斂性得到了證明,但后者至今沒有結(jié)果。本文主要解決模型(1)參數(shù)基于EM算法的極大似然估計的收斂性。
2 基于EM算法的參數(shù)極大似然估計[2][3]
假定模型(1)中關(guān)于隨機誤差ε~N(0,σ2I),則得到對數(shù)似然函數(shù)為
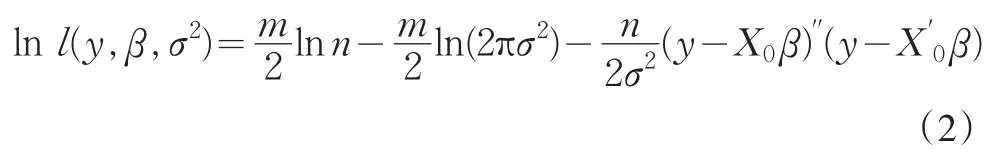
一般假定σ2已知,而y是未知的。EM算法的E步即在(2)兩邊取關(guān)于y的條件數(shù)學期望,其密度函數(shù)f(y|β(i))(β(i)是β在第i次迭代的估計值)可以由隨機誤差的分布導出,于是得到
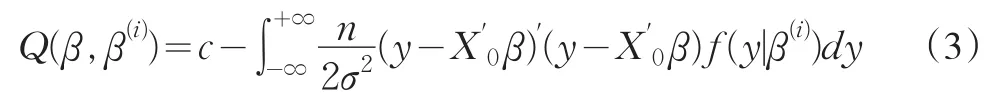
EM算法的M步即為求Q(β,β(i))的極大值。將條件密度函數(shù)代入化簡,(3)的極大化相當于對下式的極小化:
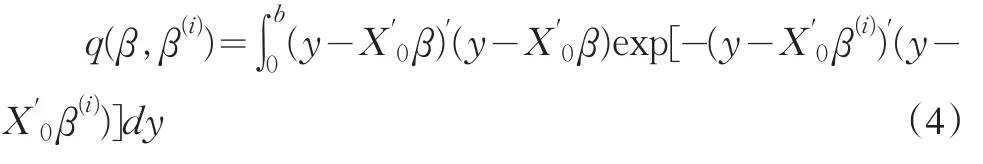
記使q(β,β(i))在約束條件下取極小值的β的解為β(i+1),獲得β(i+1)就實現(xiàn)了EM算法的M步,將β(i+1)作為下一次迭代的初值代入(4)式,重復迭代即可得到序列,直到求解的誤差小于預(yù)定精度<ε)為止。
3 基于EM算法的極大似然估計的收斂性
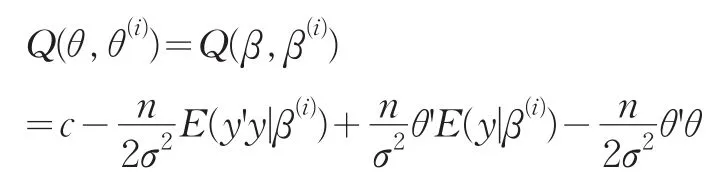


若令A(yù)=(H'?X0'),b=(1,0,0,…,0)',λ2=(k1,k2,…,kp),λ=(λ1,λ2)',λ1和ki(i=1,2,…,p)都是實數(shù),則(6)式可轉(zhuǎn)化為其對偶問題

其中,Aλ-g=θ,λ2≥0。若令A(yù)'θ-v=b,其中v為松弛變量,則
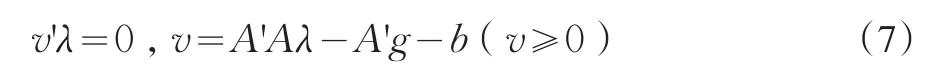
引理1對任意滿足A'θ≥b的θ都有:

證明:由(7)式可得:A'λ(i)-g(i)=θ(i+1),v(i)=A'Aλ(i)-A'g(i)-b,其中(v(i),λ(i))=0。于是有(v(i),λ(i))=0=(Aλ(i)Aλ(i))-(A'g(i),λ(i))-b'λ(i)。由A'λ(i)-g(i)=θ(i+1),得到
(Aλ(i),Aλ(i))-(A'g(i),λ(i))=(A'θ(i+1),λ(i))
于是有 (A'θ(i+1),λ(i))=b'λ(i)。因為λ(i)≥0 ,故對任意滿足A'θ≥b的θ都有:(λ(i),A'θ)=b'λ(i)。因而 (A'θ(i+1)-A'θ,λ(i))≤0 ,即 (θ(i+1)-θ,Aλ(i))≤0 ,由A'λ(i)-g(i)=θ(i+1),可得(θ(i+1)+g(i),θ(i+1)-θ)≤0。引理得證。
定理1線性不等式約束下的EM算法序列{θ(i+1)-θ(i)}是收斂的并且收斂到零。
證明:先證明極大對數(shù)似然函數(shù)序列{l(θ(i)|y)}是有界的。由模型的參數(shù)的約束條件可得:β是滿足配方條件1'pβ=1的非負的向量,從而有上界。因變量y是自變量X的配方匯總因而也是有上界的。那么觀測對數(shù)似然函數(shù){l(θ|y)}關(guān)于θ是有上界的。
由于g=-E(y|β(i))=-E(y|Λθ(i))是條件期望,它是關(guān)于θ(i)和X0的函數(shù),故可將其分解為g=-Z-Cθ(i),其中Z和C是關(guān)于X0的函數(shù)。那么EM算法的E步具有如下形式:
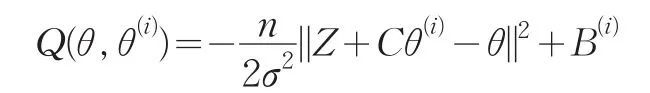
其中B(i)是關(guān)于θ(i)和X0的函數(shù)。那么由引理1可得
||θ(i+1)-θ(i)||2=||Z+Cθ(i)-θ(i)||2-||Z+Cθ(i)-θ(i+1)||2-2(Z+Cθ(i)-θ(i+1),θ(i+1)-θ(i))[≥||Z+Cθ(i)-θ(i)||2-||Z+C θ(i)-θ(i+1)||2]
又因:
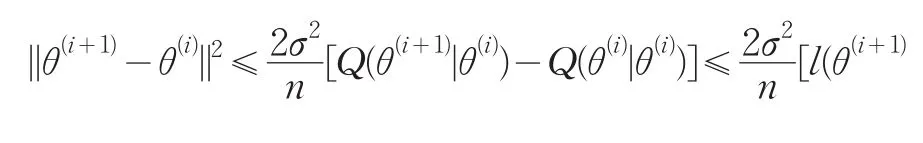
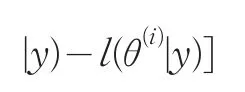
由于序列{l(θ(i)|y)}是單調(diào)[5]的,且有上界,故必收斂。因此
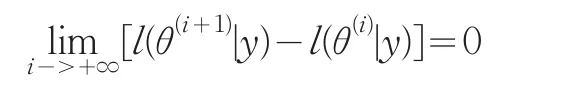
于是可得線性不等式約束EM算法序列{θ(i+1)-θ(i)}是收斂的,并且
引理2 記M(?)為從θ(i)到θ(i+1)的映射,即θ(i+1)=M(θ(i)),那么必然存在一個向量C,對任意的θ1、θ2滿足A'θ1≥b,A'θ2≥b, 都有
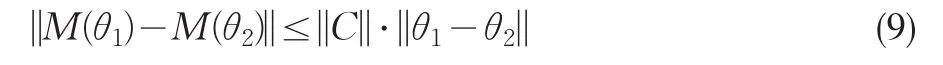
證明:顯然,映射M(?)滿足Lipschitz條件,且連續(xù)。
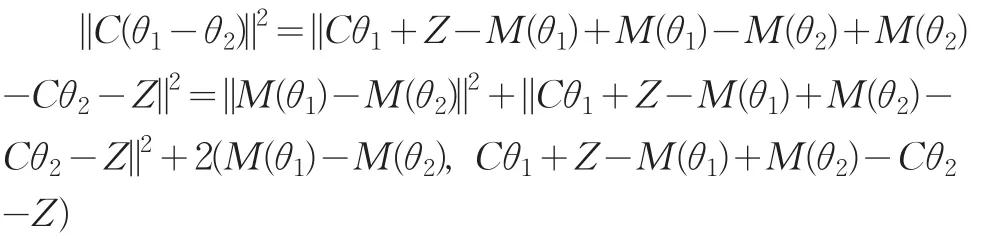
從映射M(?)的定義可知M(θ1)和M(θ2)滿足線性不等式約束,即A'M(θ1)≥b,A'M(θ2)≥b。由引理1可得
(M(θ1)-M(θ2),Cθ1+Z-M(θ1)+M(θ2)-Cθ2-Z)≥ 0
于是有:||C||?||θ1-θ2||≥ ||C(θ1-θ2)||≥ ||M(θ1)-M(θ2)||
定理2線性不等式約束下的EM算法序列{}θ(i)存在收斂的子列,且{}θ(i)中任意收斂的子列都收斂到對數(shù)似然函數(shù)l(θ|y)在線性不等式約束A'θ≥b下的最優(yōu)解。
證明:首先由于EM算法序列{}θ(i)滿足Hθ(i)=1且θ(i)>0,故{}θ(i)是有界的。那么必然存在收斂的子列,不妨設(shè){}θ(ik)是{}θ(i)序列的任一收斂子列,并令其收斂點為θ*,即由引理2可得從而得到θ*也滿足約束A'θ≥b.
由定理1知,映射M(?)是一個連續(xù)映射,故θ*=M(θ*),從而可得

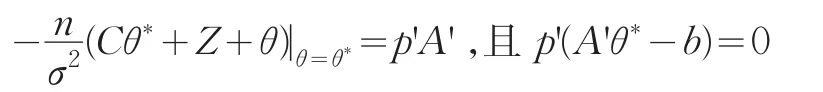
這說明θ*是Q(θ|θ*)在約束A'θ≥b下的一個K-T點,θ*為它的一個最優(yōu)解。又由于Q(θ|θ*)是關(guān)于θ的嚴格凹函數(shù),故由Kuhn-Tucker條件知Q(θ|θ*)在約束A'θ≥b下的最優(yōu)解是唯一的。因此θ*是Q(θ|θ*)在約束A'θ≥b下的唯一最優(yōu)解。而由θ*的唯一性,可知序列{}θ(i)是的任何收斂子列都收斂到Q(θ|θ*)在約束A'θ≥b下的最優(yōu)解。

若θ1=θ2,則序列收斂。若θ1≠θ2,即θ1>θ2,則序列必定存在兩個收斂子列,滿足

[1]Tong Hengqing.Evaluation Model and Its Iterative Algorithm by Alter?natingProjection[J].MathematicalandComputerModelling,1993,18(8).
[2]Hengqing Tong,Shaojun Zhong,Tianzheng Liu,Yanfang,Deng.Biosta?tistics Algorithm:Evaluation Model with Convex Constraint and Its Pa?rameters Estimates[C].The 1st International Conference on Bioinfor?matics and Biomedical Engineering,2007.
[3]童恒慶,余超,趙旭杰.凸約束廣義線性回歸模型的參數(shù)估計及算法[J].應(yīng)用數(shù)學,2008,21(4).
[4]Dempster,A.P.,Laird,N.M.,Rubm,D.B.Maximum Likelihood from Incomplete Data Via the EM Algorithm(with Discussion)[J].Journal of the Royal Statistical Society,Series B,1977,(39).

