開關磁阻電動機轉矩脈動抑制方法研究
劉 琴,馬瑞卿,張慶超
(西北工業大學,陜西西安710072)
0引 言
開關磁阻電動機(以下簡稱SRM)因具有結構簡單、成本較低、工作可靠、效率高、控制方便、調速性能好等優良特性[1],成為具有強競爭力的一種調速及伺服電動機,現已在很多領域得到應用。然而由于SRM的雙凸極結構引起的磁路非線性和飽和效應[6],使得其存在噪聲及轉矩脈動,導致它在如伺服系統和電器等多種領域不能廣泛應用。因此為了獲取更好的SRM的動靜態性能,如何抑制噪聲和降低轉矩脈動已經成為當今SRM控制系統的研究重點。本文正是從控制角度出發,研究使SRM轉矩脈動最小化的控制方法。
1轉矩分配函數法
轉矩分配函數(TDF)是用來表示SRM的轉子位置角和各相繞組所期望的轉矩之間的關系。它是通過選擇合適的轉矩分配函數來規劃各相電流,從而使各相繞組所產生的轉矩之和等同于總期望得到的轉矩,以此來減小轉矩脈動[2]。
根據TDF的定義,得到SRM須滿足的兩個條件[3]:(1)SRM的每相繞組的實際電流能夠與轉矩分配函數計算得到的期望電流相一致;(2)在任意時刻,所得到的SRM各相繞組的轉矩分配函數的和等于1。TDF原理圖如圖1所示。
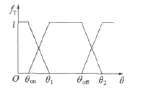
圖1 TDF原理圖
最簡單常用的轉矩分配函數為梯形波,同時SRM各相繞組的導通狀態分為以下三個過程:
(1)θon≤θ<θ1階段,導通相的期望轉矩按照函數fT(θ)逐步增加,同樣的關斷相的期望轉矩按fT(θ)來減小,SRM的總參考轉矩T*是由兩相繞組的轉矩疊加而成。
(2) θ1≤θ< θoff階段,導通相單獨導通,其轉矩值恒為T*。
(3) θoff≤θ≤θ2階段,與階段(1)類似。
本文在梯形波TDF的基礎上,采用二次曲線將梯形上升沿和下降沿平滑化,使得電流波形更為理想,如下:
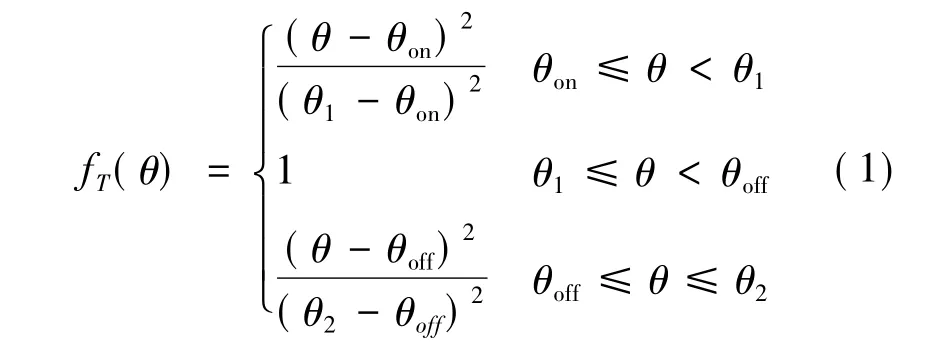
SRM每相繞組的期望轉矩:
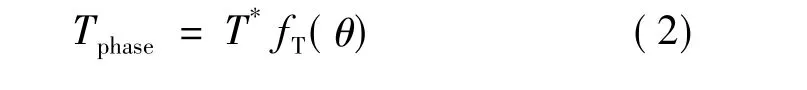
本文的TDF仿真結果如圖2所示,圖3是轉矩分配函數的仿真模型。
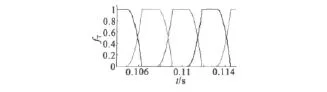
圖2 TDF仿真結果
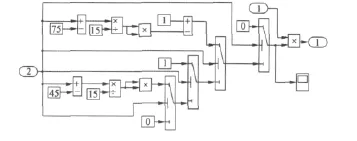
圖3 轉矩分配函數仿真
在轉矩分配函數法中,SRM轉矩不是直接控制的,是由函數T=f(i,θ),準確求得其相電流對應于轉矩和轉子位置角的逆函數關系i=f-1(T,θ),再根據期望轉矩求得對應的期望相電流,來實現SRM瞬時轉矩的有效控制。
2直接轉矩控制技術
2.1轉矩特性分析
SRM的運行遵循“磁阻最小原理”,即磁通總會沿著磁阻最小的路徑閉合。通過控制SRM定子各相繞組的順序產生磁場,這樣轉子就會有向磁阻最小的位置轉動的趨向,產生連續轉矩使電機運轉。為簡化分析,突出SRM的基本物理特性,通常采用線性模型分析電機工作的基本特性和各參數間的相互關系[4]。
施加在各定子繞組端的電壓方程:
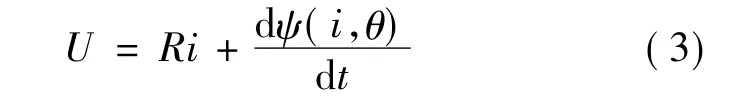
式中:i為繞組相電流;R為繞組相電阻;ψ(i,θ)為相磁鏈。從電源發出的功率:
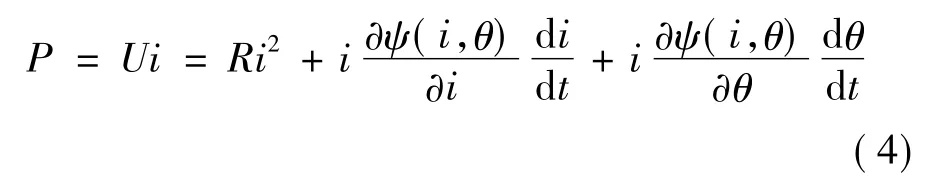
由于功率Ri2消耗在電機定子繞組上,所以從電源到磁場的有功功率:
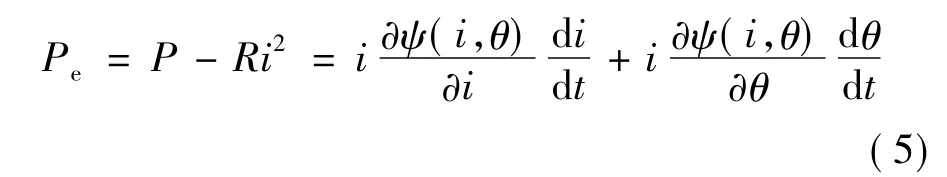
在某一時間dt內,這部分有功功率的一部分會作為機械能Wm做功,輸出到負載;其余的Wf保留在磁場中作為磁場儲能,即有:
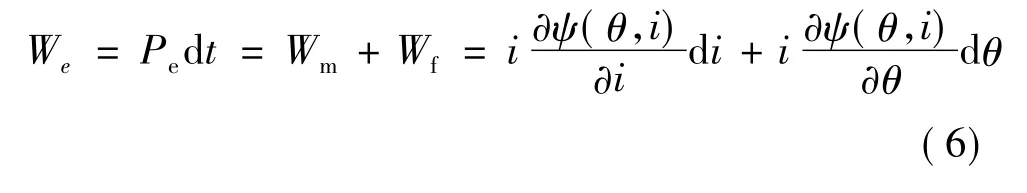
在一個控制周期中,電機的繞組電流可以認為是恒定不變的,從而得到電機的瞬時轉矩:
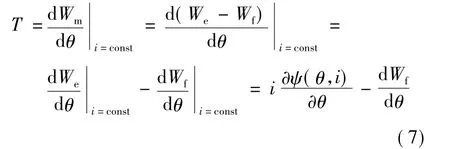
SRM的高度磁飽和性使得電機的磁場儲能幾乎不會隨著轉子位置角θ的變化而變化。從而式(7)瞬時轉矩表達式中的第二項一般非常小,可忽略,即:
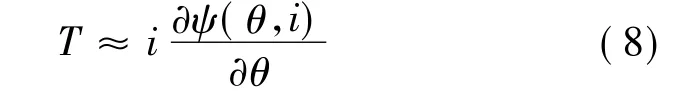
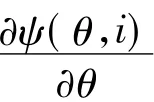
可見,直接轉矩控制方法的目標及方法:(1)為使電機的定子磁通向量保持為一恒定幅值,可選取合適的電壓矢量進行控制,從而形成近似圓形或多邊形的定子磁鏈的運動軌跡;(2)為把轉矩控制在一個限定大小的滯環寬度內,可通過定子磁鏈向量的加速和減速來控制。
2.2電壓空間矢量狀態
三相SRM的每相繞組電流雖都是單向流動,但其繞組的電壓只存在三個狀態[5],如圖4所示。
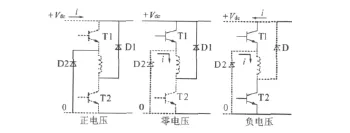
圖4 三種SRM繞組的電壓矢量
當SRM其中一相繞組k相的兩個開關管同時導通時,定義該電壓狀態Sk為1。一個開關管導通另一個關斷,繞組電流不為零時,該電壓狀態Sk為-1。兩個開關管同時都關斷,繞組上的電流只通過續流二極管流動時,電壓狀態Sk為0。這樣就得到6個相差 但幅值相同的電壓矢量,如圖5所示。
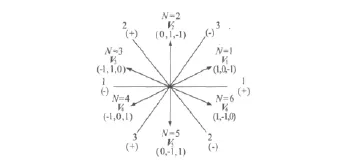
圖5 6個電壓矢量的分布及分區
圖5中顯示的6個電壓矢量為V1~V6,它們將整個范圍分成均勻的六個小區域N1~N6。
2.3直接轉矩控制表的建立
轉矩和磁鏈矢量都是通過滯環直接控制的,圖6是磁鏈的控制原理示意圖。
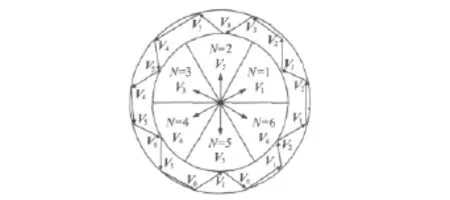
圖6 磁鏈控制原理示意圖
假如定子磁鏈位于第j區,可通過選擇電壓矢量υj+1或者υj-1來增大磁鏈,反之可選擇υj+2或υj-2來減小磁鏈。轉矩控制是通過相對于轉子運動的磁鏈的加速或減速實現的,要增加轉矩時,選擇超前于定子磁鏈的電壓矢量。如此時磁鏈位于第j區域,就可選擇電壓矢量υj+1或υj+2來增加轉矩;類似地要減小轉矩時,可以選擇υj-1或υj-2。根據上述分析,得到一個磁鏈和轉矩控制的開關表,即電壓空間矢量選擇表[4],如表1所示。

表1 磁鏈和轉矩控制開關表
3系統仿真研究
根據SRM兩種轉矩控制方法的原理分析,在MATLAB/Simulink中建立SRM轉矩分配函數法和直接轉矩控制法的系統仿真模型,如圖7和8所示。三相6/4結構SRM模型仿真參數:額定功率60 kW;額定電壓240 V。其中直接轉矩控制仿真中給定磁鏈為0.36 Wb。為了說明轉矩分配函數法與直接轉矩控制法相對于傳統電流斬波控制(CCC)的優勢,本文同時在三種控制方式下進行了轉矩及轉速的仿真并對其結果進行分析。在電流斬波控制方式下所采用的電流滯環寬度為±5 A,電流斬波上限為200 A,開通角為45°,關斷角為75°。轉速仿真也是為了觀察轉矩的脈動影響。
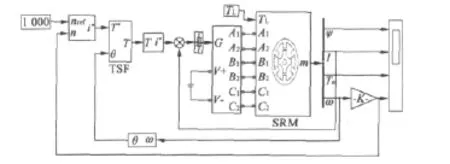
圖7 SRM轉矩分配函數法控制仿真圖
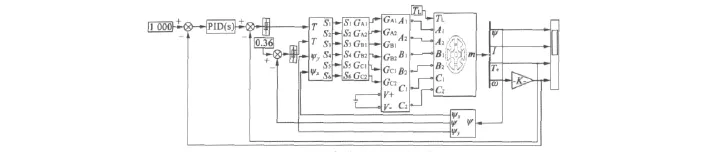
圖8 SRM直接轉矩控制仿真圖
3.1 磁鏈軌跡
圖9為三種控制方式下仿真結果。由圖中的定子空間磁鏈軌跡看出:直接轉矩控制方式下的磁鏈幅值變化波動被限定在滯環寬度范圍內,且定子空間磁鏈軌跡為近似圓形,效果好于轉矩分配函數法;而轉矩函數法的磁鏈軌跡又優于電流斬波控制。電流斬波控制方式下各相電流在換相期間,電流幅值的變化大,使得磁鏈的幅值也有較大的波動,因而轉矩受到磁鏈的影響也就產生了較大的脈動。相比磁鏈幅值,若在小范圍內波動則能降低電機損耗及轉矩脈動,所以直接轉矩控制法的轉矩脈動會小于另兩種控制的轉矩波動。
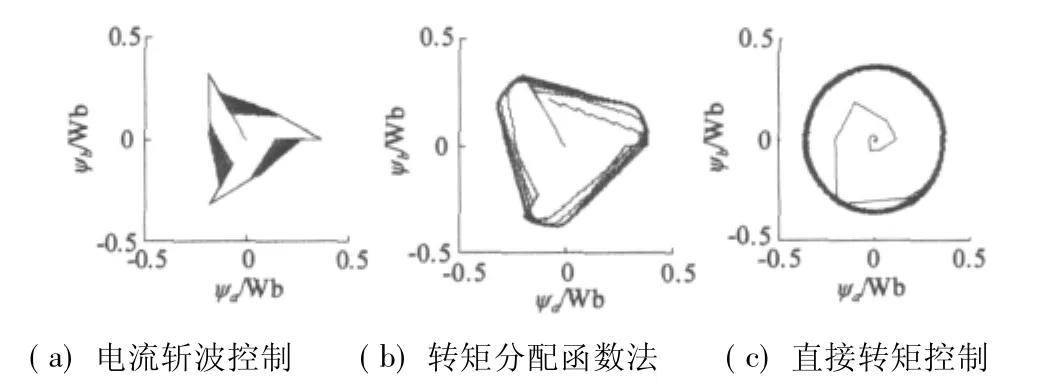
圖9 三種控制方式下定子空間磁鏈軌跡圖
3.2 轉矩波形
SRM的三種轉矩控制方式下轉矩波形如圖10所示。電流斬波控制下,轉矩波動幅度約為120 N·m,范圍在20~140 N·m之間;轉矩分配函數控制方法下轉矩波動幅度約為20 N·m,范圍約在5~25 N·m間;直接轉矩控制方法下,轉矩波動幅度僅為1.5 N·m,范圍約為13.5~15 N·m。從圖中可看出,后兩種轉矩控制方式大大降低了SRM系統的轉矩脈動。
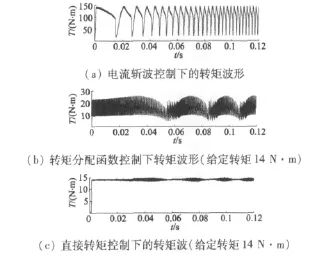
圖10 三種轉矩控制方式下的轉矩波形圖
3.3負載變化情況下的轉矩、轉速波形
三種轉矩控制方式的仿真中都加入速度閉環。轉速給定為1 000 r/min,在0.2 s時加入14 N·m的負載,0.3 s時移除,則各轉矩和轉速波形如圖11所示。
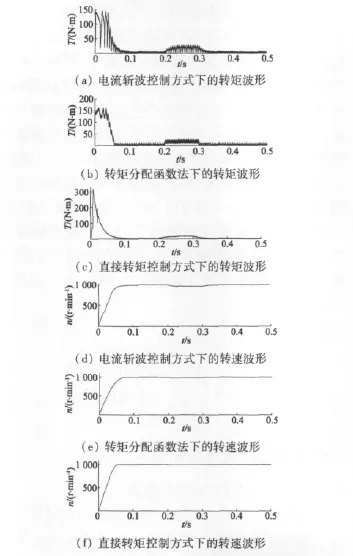
圖11 三種轉矩控制方式下轉矩及轉速波形圖
由圖11中三種控制方式下負載變化時轉矩波形的仿真結果對比可以看出:
(1)轉矩分配函數和直接轉矩控制下SRM輸出轉矩波動明顯減小,波動幅值遠遠小于電流斬波時轉矩的波動。尤其是直接轉矩控制下,即使負載發生變化的情況下,其最大的轉矩脈動波動也僅約為3 N·m;
(2)在整個范圍內電流斬波控制方式下的轉矩脈動都很大,特別在起動過程中,會影響電機的起動性能。
而從轉速波形對比可以看出:三種控制方式下在0.2 s負載變化后,電流斬波控制方式下轉速降低了5%,轉矩分配函數法控制下轉速下降2%,而采用直接轉矩控制時轉速僅下降0.3%,系統的動態性能和速度的平滑性逐步提高。同時,兩種轉矩控制方式下的平均起動轉矩明顯大于電流斬波控制方式下的起動轉矩,起動時間相對縮短。
4結 論
本文對仿真結果的分析,可得出以下三個結論:
(1)轉矩分配函數法和直接轉矩控制技術較電流斬波控制方法都可大大減小轉矩脈動,對抑制轉矩脈動有良好效果。特別是直接轉矩控制能將磁鏈矢量幅值較好地控制在滯環寬度內,使電機轉矩很好地被控制在期望范圍內。
(2)直接轉矩控制技術改善了轉矩和速度的平滑性,提高了起動性能,系統的動靜態性能良好。
(3)直接轉矩控制直接、算法簡單,易行于在實際中推廣應用,是解決SRM電機轉矩脈動問題的有效且可行的方法。
[1] 李琳娜.開關磁阻電機運行噪聲的研究[J].長春工程學院學報,2010,11(1):45-47.
[2] 溫浩,潘再平.開關磁阻電機的轉矩分配滑模控制[J].微電機,2011,44(12):25-28.
[3] 范正翹,王平.開關磁阻電動機轉矩脈動的智能抑制方法[J].微特電機,2002(2):28-30.
[4] 王衛東,張奕黃,陳忠松,等.開關磁阻電機直接轉矩控制[J].機械研究與應用,2008,21(1):125-128.
[5] 黃卓冕,譚平,瞿遂春.開關磁阻電機的直接轉矩控制技術研究[J].湖南工業大學學報,2010,24(4):88-91.
[6] Wang Mianhua.The fuzzy-PI control of switched reluctance motor based on DTC[C] //2009 International Conference on Measuring Technology and Mechatronics Automation.Zhangjiajie,2009.

