特種函數旋轉變壓器諧波補償的有限元分析
張艷麗,楊為華,劉永平,邵煥清,桑 瑜
(中國電子科技集團第二十一研究所,上海 200233)
0 引 言
特種函數旋轉變壓器(以下簡稱特函旋變)誤差補償方法在文獻[1]中已進行了詳細的理論分析,本文采用二元有限元計算方法對一種55#機座的特殊函數的旋轉變壓器進行諧波補償仿真分析,并通過試驗數據進行分析驗證。
1 特函旋變的原理
特函旋變由定、轉子兩部分構成,定子激磁,通過電磁感應,轉子方輸出一相與定子機械轉角成特殊函數關系變化的信號,結構圖如圖1所示,原理圖如圖2所示。輸出電壓表達式:
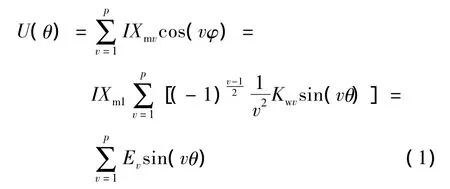

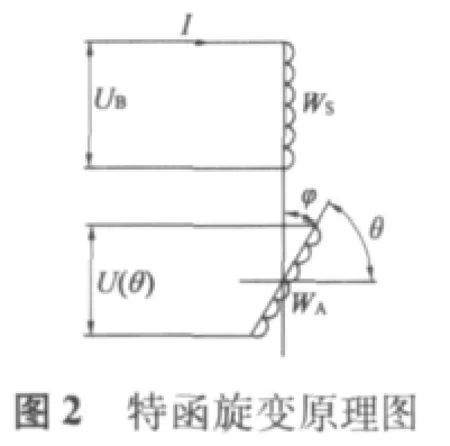
2 有限元分析模型
特函旋變輸出電壓U(θ)取勝轉子轉角θ的變化可以復現用戶要求的函數關系,本文有限元仿真分析的特函旋變的曲線如圖3所示。
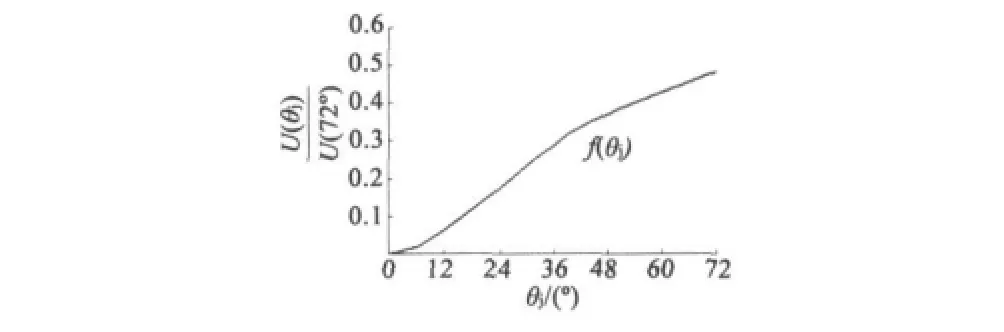
圖3 特函旋變曲線
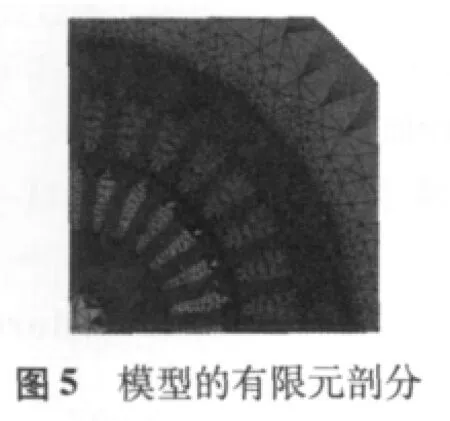
特種函數f(θj)旋轉變壓器二維暫態磁場有限元仿真模型的基本參數如表1所示,假定該旋轉變壓器工作理想狀態,加在定子方激磁繞組上的電壓E1=30 V,激磁頻率f=400 Hz。為了分析諧波補償對旋轉變壓器精度的影響,建立兩個仿真模型,除定子繞組的匝數不同外,其余各種參數定義相同。定、轉子均采用同心式繞組,模型1的定子繞組未進行諧波補償,模型2中定子繞組是通過文獻[2]中誤差補償計算方法進行了三次諧波補償,圖4為特函旋變仿真模型。為使剖分單元合理,采用靜態場剖分,暫態場計算,圖5為模型的有限元剖分圖,有140000多個剖分單元。定、轉子鐵心材料為軟磁合金帶 1JH3,厚0.35 mm,氣隙0.3 mm。

表1 仿真模型參數
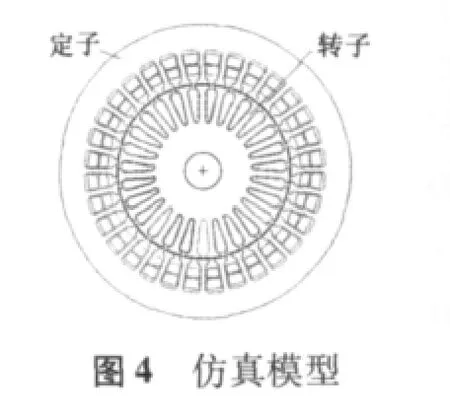
3 有限元計算結果及分析
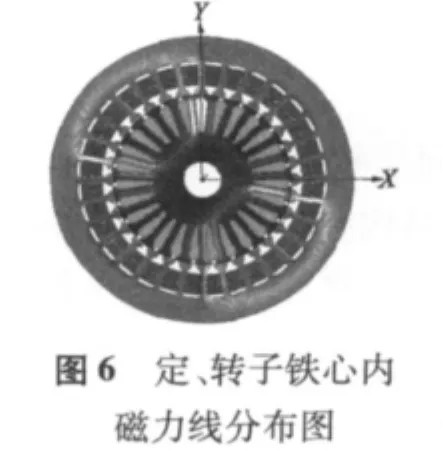
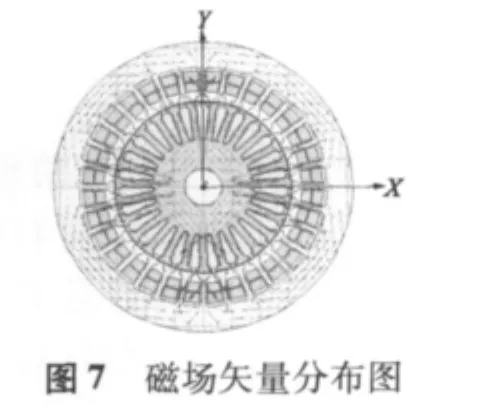
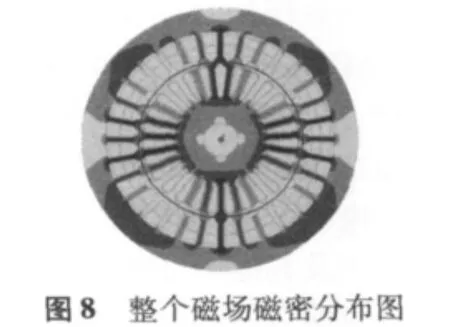
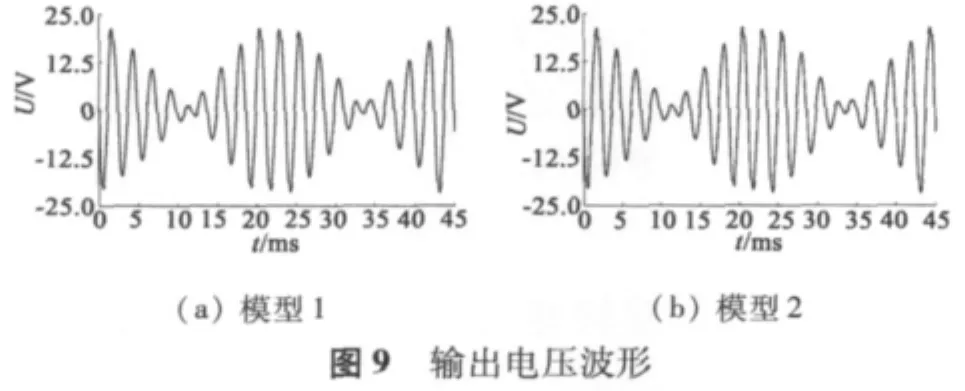
特函旋變二維暫態磁場有限元仿真結果如圖6~圖8所示。由圖可知,該旋變的齒部磁密最大,設計時主要考慮齒部的磁飽和。特函旋變模型在一個電周期內的輸出電壓波形如圖9所示。該特種函數f(θ)的使用范圍是 0°~ 72°,每 6°測一點。
三次諧波補償前有限元仿真計算誤差值Δfm如圖10(a)所示,最大誤差點為30°位置,誤差值約為-6.8‰,且誤差值偏負值。
三次諧波補償后有限元仿真計算誤差值Δf'm如圖10(b)所示,最大誤差點為6°位置,誤差值約為+3.9‰,通過諧波補償,誤差值明顯降低,且誤差值均勻分布在橫軸線兩側。
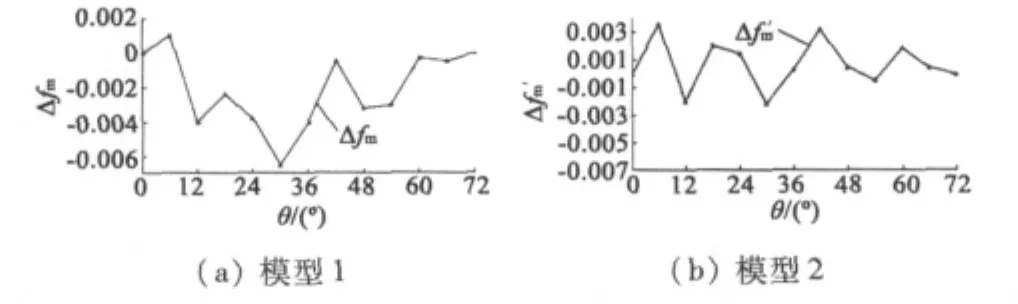
圖10 有限元計算誤差值
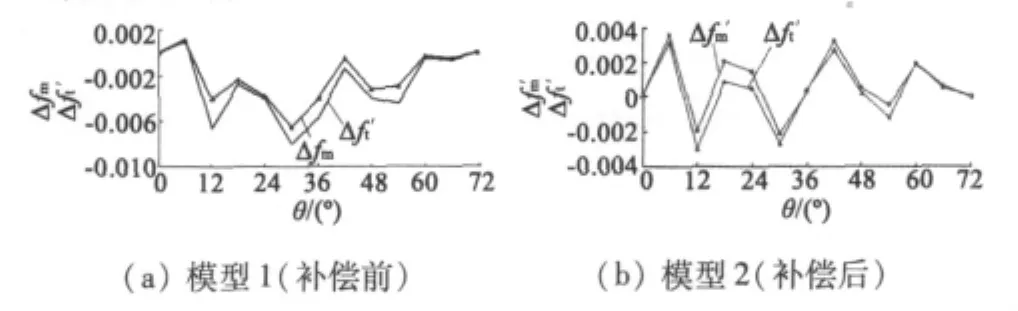
圖11 計算值與實測值對比圖
三次諧波補償前后實測誤差對比曲線如圖12所示。本文試驗數據曲線均為平均值,具體試驗數據如表2所示。未進行諧波補償前零級品為0,補償后零級品為96%,產品精度顯著提高。
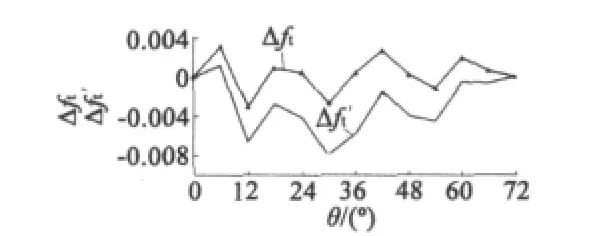
圖12 三次諧波補償前后實測誤差對比曲線
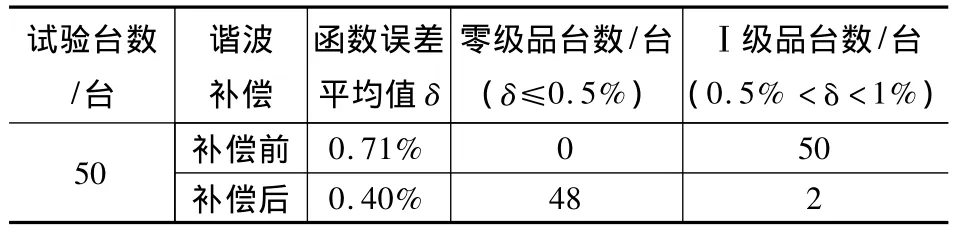
表2 特函旋試驗數據
4 結 語
通過特函旋變二維暫態磁場有限元仿真結果和實驗數據分析表明,采用有限元仿真分析有效驗證了諧波補償對降低誤差的正確性及有效性,有限元磁場仿真有助于旋轉變壓器的設計及優化。二維磁場仿真忽略了定、轉子鐵心的端部效應,對轉子斜槽也無法計算。為提高計算的精確度,考慮轉子的斜槽情況,應進一步研究旋轉變壓器的三維磁場仿真技術。
[1]田恒安,陳燕玉,廖超宏,等.特種函數旋轉變壓器設計計算[J].微特電機,1976(1):39 -64.
[2]張艷麗.特種函數旋轉變壓器的諧波補償[J].微特電機,2008(12):31-33.
[3]Lang C W.Special synchros for function generation[J].Control Engineering,1968,15(12):75 -78.

