一種基于截距的圓形窗口線裁剪算法
任洪海, 郭發軍, 王艷娟
(大連交通大學軟件學院數字媒體教研室,遼寧 大連 116052)
線裁剪是計算機圖形學的一個基本操作,作為圓形窗口線裁剪求交過程較為復雜,快速確定線段是否與窗口相交以及交點計算是這類算法的關鍵。近年來很多學者提出了圓形窗口的線裁剪算法。如文獻[1-2]直接將線段參數方程代入圓形窗口的代數方程,通過求解一元二次方程實現裁剪,效率較低。文獻[3]經過矩形單側排除預處理后,利用圓心到直線段距離以及從圓心向直線段所引的垂直射線來判別直線段與圓形窗口的位置關系,但點-線距離以及旋轉矢量法的計算量都很大。文獻[4]通過制備規范化交點表避免了二次方程的運算,但需要很大精力建立復雜的規范化交點表。文獻[5]利用常規外切正方形一次編碼及旋轉外切正方形二次編碼排除部分圓形窗口之外的線段,在線段位置不確定的情況下,需要進行多重編碼,而事實上并未簡化求交過程。文獻[6]通過坐標變換使線段與圓的位置關系轉化為x軸與圓的位置關系,其中坐標變換和其逆變換都很費時。文獻[7]通過圓切線斜率與線段斜率的比較確定線段是否與圓形窗口相交,一定程度提高了裁剪效率,不過求圓切線斜率也涉及到開方等復雜計算。
本文提出一種基于線段在兩坐標軸上截距的圓形窗口線裁剪算法。經過簡單測試,排除兩端點都在圓外切正方形某邊界之外的線段,并確定兩端點都在圓形窗口內或一端點在圓形窗口內而另一端在圓形窗口外這兩種情況中線段與圓形窗口的位置關系。對于兩端點都在圓形窗口之外的情況,求線段所在直線相交x和y兩坐標軸上的截距,并進行如下判斷:如果線段所在直線在x或y任意坐標軸上截距的絕對值小于或等于圓半徑 r,通過區分兩端點在相交軸的同側還是異側可快速確定線段與圓形窗口的相交關系;否則,線段或不與圓形窗口相交或與圓形窗口相交于兩截距所在半軸約束的象限上。根據該象限上外切正方形的頂點相對于線段所在直線的位置關系排除不與圓形窗口相交線段后,再通過線段與外切正方形兩交點任意一個引射線相交外切正方形邊所得到的交點與另一交點坐標相比較確定線段是否與圓形窗口相交。該方法可以快速確定線段與圓形窗口的位置關系,明顯提高裁剪效率。
1 基本定義
不失一般性,假設裁剪算法中圓形窗口的圓心為坐標原點。如果圓心在其它位置,通過坐標系平移將圓心平移到坐標原點。被裁剪線段的兩個端點設為p1(x1,y1)和p2(x2,y2)。
定義 1本文中的“外切正方形”指四邊平行于坐標軸,且與圓形窗口相切的正方形。
通過端點pi(xi,yi)(i取1或2)的兩坐標值與外切正方形的4個邊界相比較確定該點與邊界的位置關系:
如果xi<-r,該點在左邊界外側;否則,該點在左邊界內側或上;
如果xi>r,該點在右邊界外側;否則,該點在右邊界內側或上;
如果yi<-r,該點在下邊界外側;否則,該點在下邊界內側或上;
如果yi>r,該點在上邊界外側;否則,該點在上邊界內側或上。
從而得出線段端點相對于外切正方形及圓形窗口的位置關系為:
如果線段的端點在某一邊界的外側,則該端點一定在外切正方形之外,該端點也在圓形窗口之外。
如果線段的端點在4條邊界的內側或上,則該端點在外切正方形的內側或上,再進一步判斷端點與圓形窗口的位置關系:
設端點pi(xi,yi)(i取1或2)到圓形窗口圓心距離的平方為:

定義 2過圓心向線段p1p2引垂直射線l,稱射線l為該線段的主射線。
區分線段兩端點p1、p2在其主射線的異側還是同側的方法為:
1)當線段p1p2為水平線(即y2=y1)時:如果x1與x2異號,則兩端點 p1、p2分別在線段p1p2主射線l的異側;否則,兩端點p1、p2分別在線段p1p2主射線l的同側。
2)當線段p1p2非水平線(即y2≠y1)時:如果 min(y1/x1,y2/x2)<(x1-x2)/(y2-y1)<max(y1/x1,y2/x2),則兩端點p1、p2分別在線段p1p2主射線l的異側;否則,兩端點p1、p2分別在線段p1p2主射線l的同側。
2 線段與圓形窗口相交判斷
當線段兩端點都在外切正方形某邊界之外時,線段一定在圓形窗口之外,排除該線段(如圖 1線段 l1)。當線段兩端點都在圓形窗口之內時,線段一定在圓形窗口之內,保留該線段(如圖 1線段 l2)。當線段一端點在圓形窗口之內而另一端點在圓形窗口之外時,線段與圓形窗口相交,實交點到內端點間線段為裁剪結果(如圖1線段 l3)。當線段兩端點不同時在外切正方形某邊界之外且都在圓形窗口之外時,通過線段所在直線相交于兩坐標軸上的截距與圓半徑的比較分情況確定線段與圓形窗口的位置關系,具體判斷如下:
1)線段所在直線相交x或y任意坐標軸上截距的絕對值小于或等于圓半徑r的情況。
定理1對于圓心為坐標原點的圓,如果直線相交x或y任意坐標軸上截距的絕對值小于或等于圓半徑r,可得該直線一定與圓相交。
證明:過圓心向直線做垂線段,在包含垂線段與x或y坐標軸上截距邊的直角三角形內,垂線段(作為直角邊)一定小于截距邊(作為斜邊)。因此,如果截距的絕對值小于或等于 r,圓心到直線的距離一定小于圓半徑 r,從而直線一定與圓相交。
線段p1p2所在的直線方程為

根據定理1很容易得出如下結論:當線段兩端點都在圓形窗口之外且線段所在直線相交x或y任意坐標軸上截距的絕對值小于或等于圓半徑r時,如果線段兩端點在截距的絕對值小于r那個相交軸的異側,則線段一定與圓形窗口相交(如圖 1線段 l4);如果線段兩端點在截距的絕對值小于r那個相交軸的同側,則線段一定不與圓形窗口相交(如圖1線段l5)。判斷過程如下:
如果-r≤a≤r,且 y1與 y2異號, 則線段與圓形窗口相交;
如果-r≤a≤r,且 y1與 y2同號, 則線段不與圓形窗口相交;
如果-r≤b≤r,且 x1與 x2異號, 則線段與圓形窗口相交;
如果-r≤b≤r,且 x1與 x2同號, 則線段不與圓形窗口相交;
如果線段為水平線段或垂直線段時,只求一個方向截距進行判斷即可。
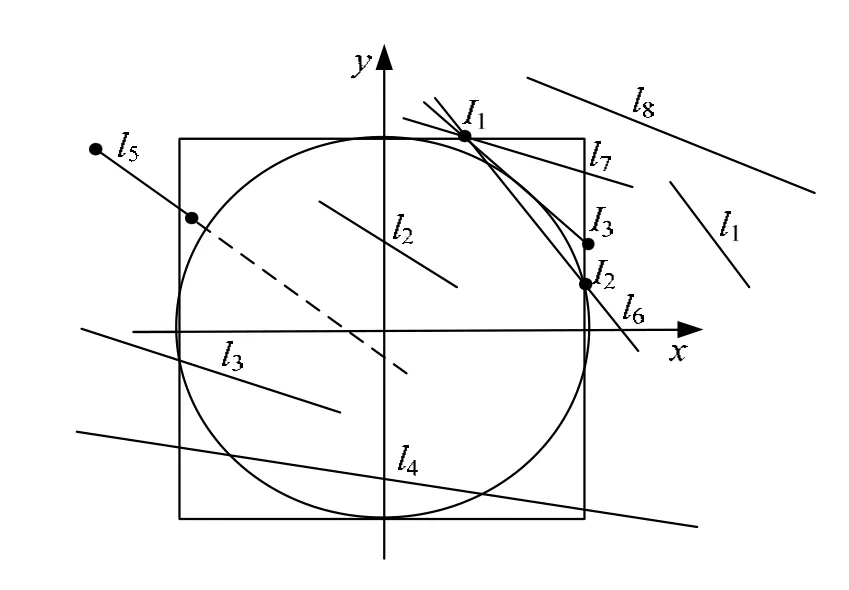
圖1 主要類型線段相對于圓形窗口的位置關系
2)線段所在直線相交x和y兩坐標軸截距的絕對值都大于圓半徑r的情況
當線段所在直線相交x和y兩坐標軸截距的絕對值都大于圓半徑r時,線段與圓形窗口位置關系有兩種情況:線段不與圓形窗口相交或線段與圓形窗口相交于兩截距所在半軸約束的象限上。通過測試兩方向截距所在半軸對應象限上外切正方形的頂點關于線段所在直線的方向,首先判斷線段所在直線是否與外切正方形相交。如果線段所在直線不與外切正方形相交,則線段一定不與圓形窗口相交。假設兩截距分別在 x軸的正半軸與y軸的正半軸,則測試外切正方形在第1象限的頂點(r,r)關于直線的方向。
由于已求出直線在兩坐標軸上的截距 a與b,直線可應用截距式方程表示
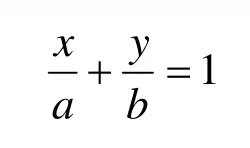
在第1象限上,如果線段所在直線相交x軸與 y軸的截距都大于圓半徑 r,則有:可得(r,0)在直線下側;同時,可得(0,r)在直線下側。
對于任意所在直線相交于外切正方形在第1象限上1/2上邊與1/2右邊的線段,將外切正方形邊界條件代入直線的截距式方程求直線與外切正方形的兩交點為。可以取兩個交點任意一個,過該交點作圓形窗口的切線。假設取作圓形窗口的切線與外切正方形在第 1象限上 1/2右邊的交點設為
根據I1I3兩點距離公式有
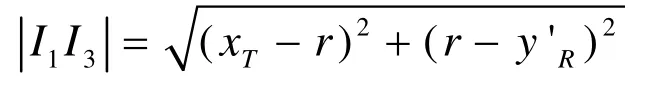
比較yR與y'R的大小可得線段所在直線與圓形窗口的位置關系:
如果 yR<y'R,可得線段所在直線與圓形窗口相交(如圖1線段l6);
如果 yR=y'R,可得線段所在直線與圓形窗口相切;
如果 yR>y'R,可得線段所在直線與圓形窗口相離(如圖1線段l7);
如果取 I2作圓形窗口的切線與外切正方形相交,則通過比較交點的x方向坐標進行判斷線段所在直線與圓形窗口的位置關系。對于與外切正方形相交于其它象限上的線段,同樣可進行類似推導,并得出相應結論。
3 裁剪算法描述



4 快速求線段與圓形窗口的交點
當被裁剪線段一端點在圓形窗口內,而另一端點在圓形窗口外,確定線段與圓形窗口有交點后,通過兩端點形成直線段參數方程代入圓方程求交點。對于大部分兩端點在圓形窗口之外的情況,由于根據被裁剪線段所在直線在兩坐標軸的截距判斷線段是否與圓形窗口相交,當確定被裁剪線段與圓形窗口有交點時,可以應用線段所在直線與兩軸坐標的交點(a,0)和(0,b)形成直線參數方程代入圓方程求交點。具體操作如下:
對于過(a,0)和(0,b)的直線,可用參數形式描述為
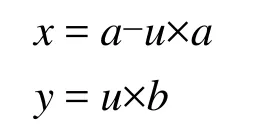
作為直線與圓形窗口的交點,必滿足:x2+y2=r2,將直線參數方程代入圓方程得
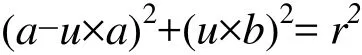
可整理為關于u的一元二次方程
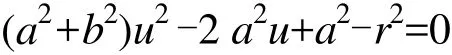
解此一元二次方程,可得
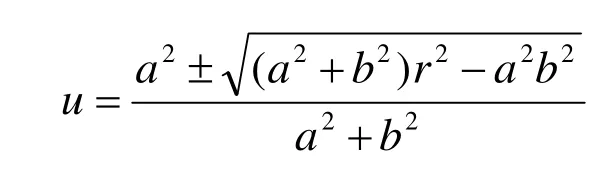
由于被裁剪線段兩端點都在圓形窗口之外,如果線段與圓形窗口有交點,則一定有兩個交點(相切時有兩相同交點),求出u值代入直線的參數方程即可得到兩個交點。此一元二次方程解中都是兩截距a、b平方與圓半徑r平方的組合,很容易構造。
5 算法分析與比較
本文根據被裁剪線段所在直線相交x、y坐標軸上的截距可以確定大部分線段是否與圓形窗口相交。對于其它不能確定相交關系的被裁剪線段,通過點與線的關系及交點坐標比較等簡單操作即可快速完成判斷。另外通過截距形成被裁剪線段所在直線的參數方程代入圓方程求交點,方程構造與求解形式都比較簡單。表1為對于幾種主要類型的被裁剪線段(圖 1所示),應用本算法進行圓形窗口線裁剪需要的主要操作及運算量。
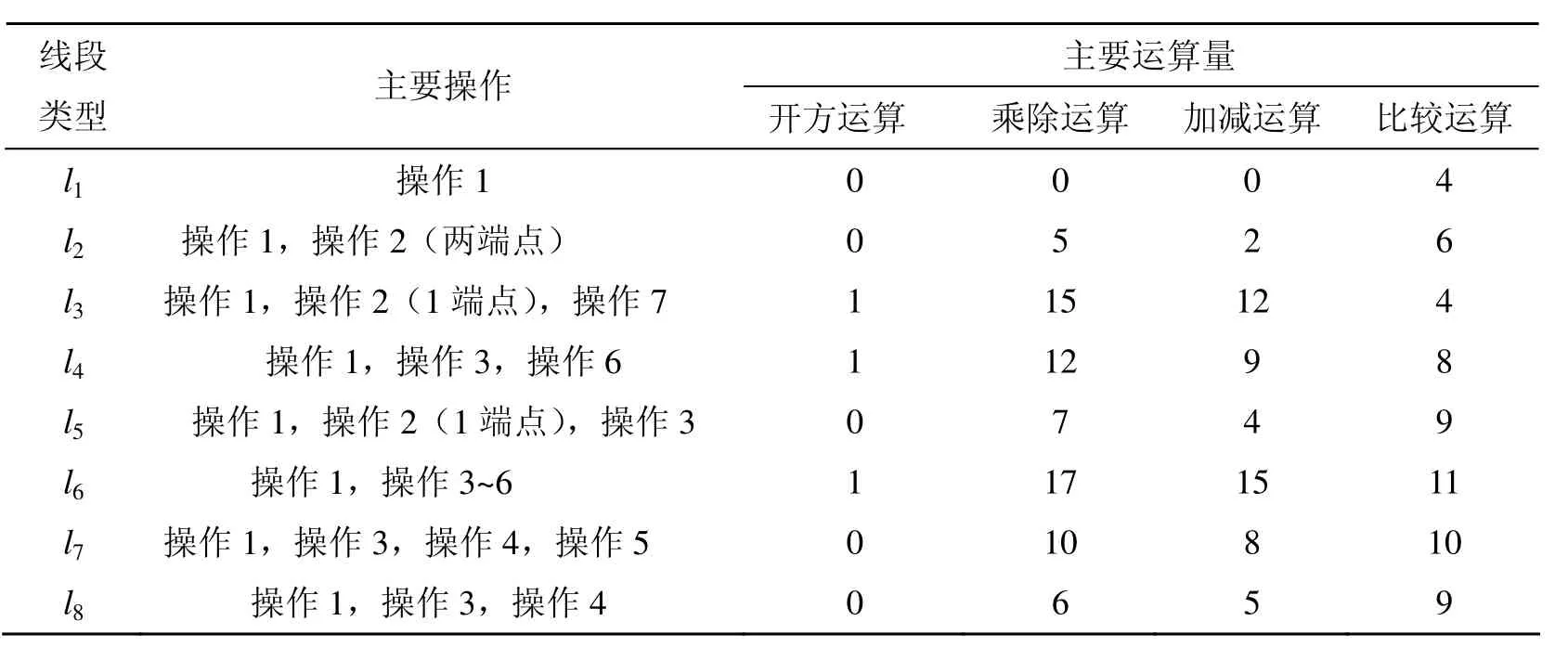
表1 幾種主要類型線段圓形窗口裁剪過程需要的主要操作與運算量
從表1可得出本算法在確定線段與圓形窗口有交點后,才應用1次開方運算求交點,其它判斷線段是否與圓形窗口相交的過程只涉及乘除、加減、比較等簡單運算。
在同等硬件條件下,應用C++編程實現文獻[3]、文獻[5]、文獻[6]、文獻[7]及新算法。表 2列出 4個裁剪算法對于不同半徑圓形窗口裁剪400萬條隨機線段所需的時間比較。

表2 4種裁剪算法裁剪400萬條線段所需時間比較(單位:秒)
由表2可以看出新算法的裁剪效率明顯高于現有的4種典型算法。
6 結 論
以二次函數作為約束條件的圓形窗口線裁剪求交過程較為復雜。本文根據線段所在直線相交兩坐標軸上的截距與窗口圓半徑r相比較,以及線段與所引切線分別相交外切正方形邊的交點坐標相比較等方法確定線段與圓形窗口的位置關系。該方法將線段與圓形窗口位置關系的兩維問題轉化成主要在 x、y兩坐標軸上或某外切正方形邊上數值比較的一維問題,從而開辟一條解決圓形窗口線裁剪的新途徑。在確定線段與圓形窗口位置關系過程中主要涉及的線段在兩坐標軸上截距的計算、點線位置關系的判斷和所引切線與外切正方形邊交點的計算等過程通過簡單比較和四則運算即可完成,不需要冪、開方和三角函數等復雜運算,從而能夠快速確定線段與圓形窗口是否相交,提高裁剪效率。本文提出的圓形窗口線裁剪算法很容易推廣到橢圓窗口的線裁剪,同時對球體等三維窗口的線裁剪也具有很強的參考價值。究與實踐[J]. 計算機輔助設計與圖形學學報,1992,4(3): 14-20.
[1] 姚涵珍,宋 鵬,張國安. 圓形窗口裁剪算法的研
[2] 劉勇奎. 圓形及橢圓形裁剪窗口[J]. 計算機工程與設計,1994,15(4): 33-37.
[3] 沈慶云,周來水,周儒榮. 一種圓形窗口裁剪的新方法[J]. 計算機輔助設計與圖形學學報,1997,9(6):538-542.
[4] 蔡 敏,袁春風,宋繼強,等. 一種快速的圓形窗口裁剪算法[J]. 計算機輔助設計與圖形學學報,2001,13(12): 1063-1067.
[5] 陸國棟,邢軍偉,譚建榮. 基于多重編碼技術的圓形窗口線裁剪算法[J]. 計算機輔助設計與圖形學學報,2002,14(12): 1133-1137.
[6] 唐 棣,單會秋. 一種基于坐標變換的圓形窗口線裁剪算法[J]. 計算機應用與軟件,2006,23(5):116-118.
[7] 任洪海,張飛俠. 一種有效的圓形窗口線裁剪算法[J]. 工程圖學學報,2011,32(5): 74-78.
[8] Hearn D,Baker M P. Computer graphics with openGL(third edition) [M]. Publishing House of Electronics Industry,2005: 315-340.

