管類鈑金結構接口幾何信息的分析與提取

毛 昕， 馬明旭， 鄭志佳

（東北大學機械工程與自動化學院，遼寧 沈陽 110004）

現代生產中，鈑金結構和制件以其工藝簡單、成本低、生產效率高、適合大批量生產等優點，在機械、冶金、石油化工、汽車、船舶、航空航天、輕工等行業中得到越來越廣泛的應用，其中，管類鈑金結構和制件占有絕大多數比重[1]。在鈑金展開中，材料的板厚處理是保證構件成形精度的重要環節。對于管類鈑金結構，包括圓周方向和接口處兩方面的板厚處理，在圓周方向常以板料中性層（在板厚與彎曲半徑比不大時，常取板料中心層）為準進行展開，而接口處的板厚處理卻常憑經驗甚至不作處理。困難主要來自兩方面：一是一種構件一個方法，難以找到較共有的、通用的規律和方法；二是對于稍復雜的構件，就難于精確處理[2]。接口板厚處理的忽略大大降低了展開和構件的成形精度。管類鈑金結構接口的主要類型如圖1所示[3]。

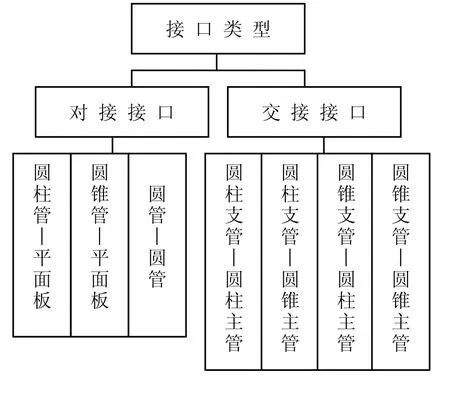
圖1 管類鈑金結構接口類型

在接口的板厚處理時，要分析和提取接口處的幾何信息。如圖2所示，圓柱支管與圓錐主管外表面相交形成交接接口，接口處板厚處理的目的是要找出兩管間的實際結合線，即接口曲線，并將其沿接口曲面素線方向映射到中性層表面得到中性層曲線，這條曲線便是中性層展開時的準確邊界曲線。在這種接口形式下，接口曲線總在主管的外表面上；但對于圓柱支管，接口曲線部分在其外表面上（外皮接觸），部分在其內表面上（里皮接觸），部分在其內外表面之間的接口曲面上，形成了里外皮間的過渡區間，各部分的分界點是求取時的特殊點。接口曲面是指支管端面過接口曲線的環帶狀曲面，它是一直紋曲面，其素線是垂直于支管相應素線、長度等于支管板厚的一小段直線。

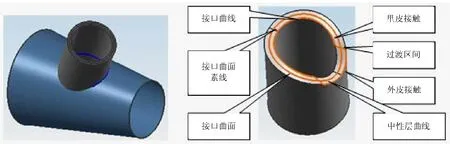
圖2 接口幾何信息

在過渡區間之外，相應接口曲面素線與平面板或主管外表面相交，其交點即為接口曲線上的點，這些點可用求截交線或相貫線的一般方法求得；在過渡區間內，相應接口曲面素線在平面板內或與主管外表面相切，其切點為接口曲線上的點。接口處板厚處理的關鍵是提取出過渡區間內接口曲線上點的位置和過渡區間端點的位置。

在對接接口中，當圓柱管或圓錐管與平面板對接時，過渡區間的接口曲線為直線，求取相對容易[3]。當圓管與圓管（圓管包括圓柱管和圓錐管）對接時，先用過兩管結合線的平面截斷構件，然后分別按圓柱管與平面板或圓錐管與平面板的情況進行處理。

在交接接口中，過渡區間內接口曲線上點的求取利用了過該點支管接口曲面素線的3個幾何性質[4]：

1）接口曲面素線與支管軸線相交；

2）接口曲面素線與主管外表面相切；

3）接口曲面素線與支管相應素線垂直。

接口處準確的板厚處理，可以使展開圖具有準確的接口展開曲線，保證了構件成形時的裝配精度，減少了裝配時的修形工作量，從而降低了生產成本，提高了產品質量；另一方面，也可以通過具有準確接口端形狀的中性層曲面來生成具有真實接口形狀的構件三維模型[5]。

1 接口幾何信息處理的圖解方法

作圖時，直接根據上述3個幾何性質，求取支管接口曲面素線與主管外表面的切點，即過渡區間內接口曲線上的點。圖3是圓柱支管與圓錐主管交接的例子，首先在支管軸線的適當位置取點K，然后過K點作主管外表面的切平面NAS（S為錐頂），AS為切線。然后過K點作垂直于支管軸線的接口曲面素線KM，其與AS的交點M即為該素線與主管外表面的切點。改變K點的位置，按上述步驟反復作圖，作出點M的軌跡曲線，其與支管外、里皮和主管外表面的相貫線相交于點M1和M2，這兩點即為過渡區間的邊界點。圖4是圓錐支管與圓柱主管交接的例子，其圖解思想與圖3相同，即求取過K點的支管接口曲面素線與主管外圓柱面的切點。不同的是，過K點的主管外表面的切平面為一側垂面，過K點支管接口曲面素線的軌跡為以K點為錐頂、素線與支管素線垂直的圓錐面，圓錐面與側垂面的交線KE與圓柱面相切于點M。

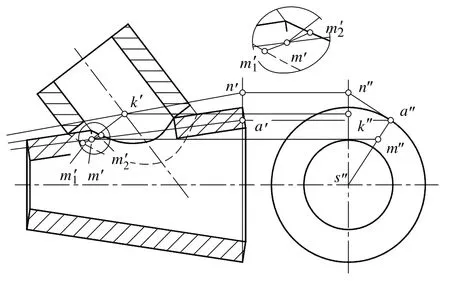
圖3 圓柱支管與圓錐主管交接

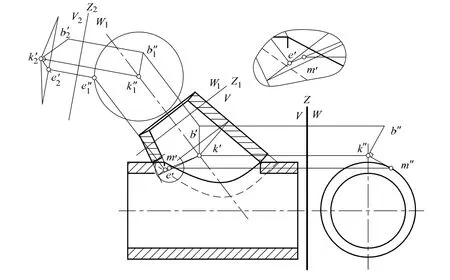
圖4 圓錐支管與圓柱主管交接

2 接口幾何信息處理的解析模型

圖解方法雖簡單、直觀，但誤差大、效率低、大型構件受場地限制。解析算法克服了這些缺點，也為計算機輔助鈑金設計提供必要的數學模型。下面僅以圖5所示的兩圓錐管交接為例說明求解規律和步驟，已知尺寸為：R1，R2，r1，L，F，H，α，β和t，主管外皮、支管外皮和支管里皮錐頂分別記為S、S1和S2。

2.1 求過渡區間內的點M

在支管軸線的適當位置取點K(0,0,zk)，過K點作接口曲面素線軌跡倒錐（底半徑為r，高為h）和主管外表面的切平面ANS（切線為AS），AS與倒錐的交點即為過渡區間內接口切線上的點M。

倒錐的方程為

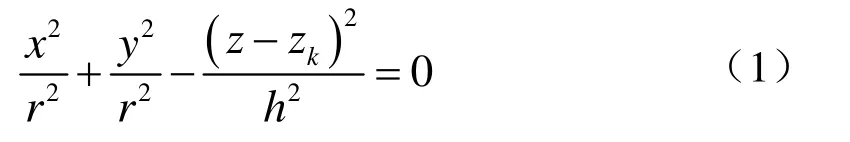
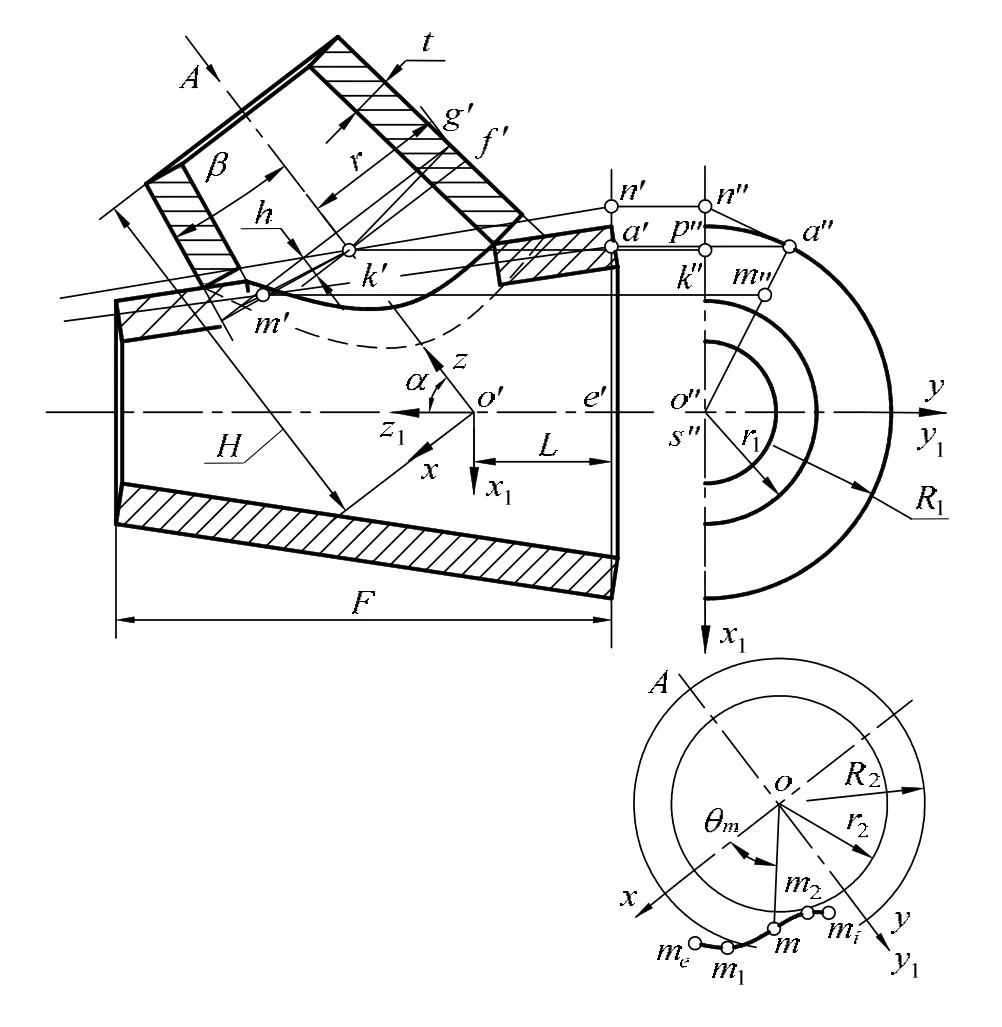
圖5 圓錐支管與圓錐主管交接

S點坐標

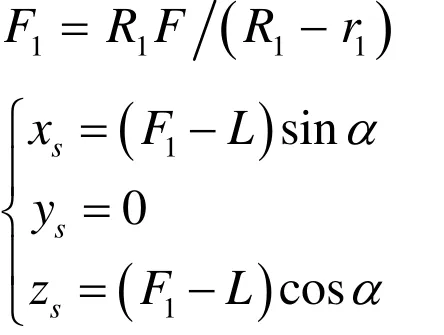
A點在o1-x1y1z1下的坐標

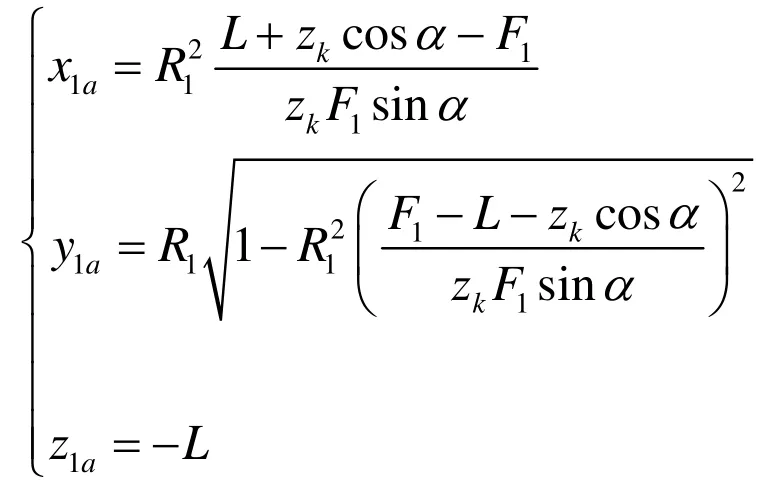
A點在o-xyz下的坐標

直線AS的方程

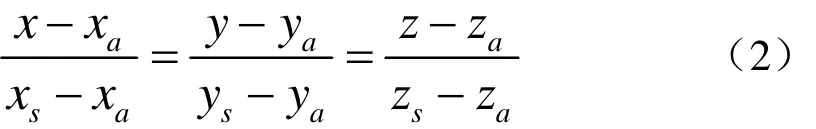
聯立方程（1）和（2），可解出M點的坐標xm、ym和zm，它們均為zk的函數。

2.2 求過渡區間的臨界點M1和M2

M1(M2)既在圓錐支管外（里）皮上，又在過渡區間內點M的軌跡上。

支管外皮錐面方程

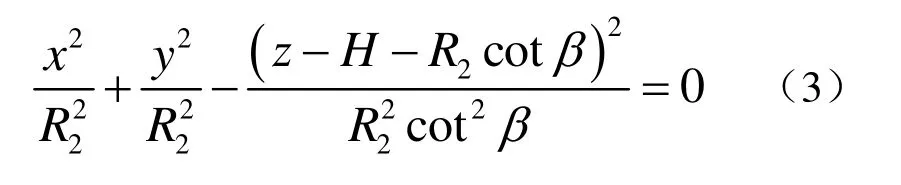
把xm、ym和zm的表達式代入式（3）并整理有

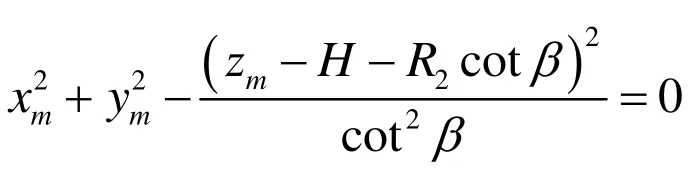
展開后為關于 zk的一元二次方程，解出 zk1，并由 2.1節可求出外皮分界點 M1(xm1、ym1、zm1)。用同樣的方法可由式（4）解出zk2和里皮分界點M2(xm2、ym2、zm2)。于是，對于過渡區間有

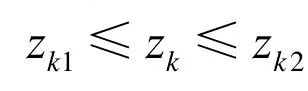
M、M1和M2點對應的θ 角（圖5中A向視圖）

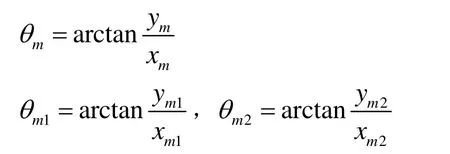
2.3 求非過渡區間的點Me（外皮）和M i（里皮）

外皮和里皮接口曲線上的點Me和Mi對應的θ角 分別為θe和θi，這些點用相應支管素線與主管外表面交點的方法求得。主管外圓錐面的方程為

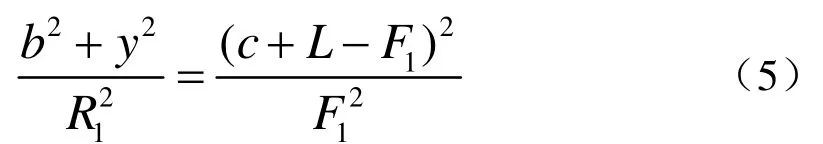
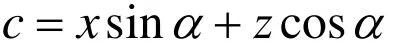
支管外皮錐頂 S1的坐標為 ( 0,0,H+R2cotβ)，對應θe角，支管外皮錐面素線的方向數為｛sinβcosθe,s inβsinθe,- cosβ，該素線的直線方程為

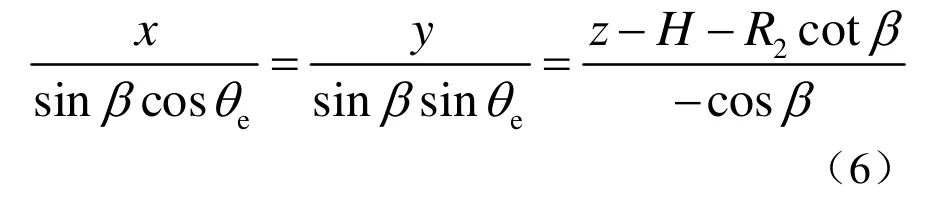
聯立式（5）和式(6)，可解出 me(xme, yme,zme)，它為θe的函數。θe的取值范圍為0°≤θe≤θ1。

同理，支管里皮對應θi角的素線方程為

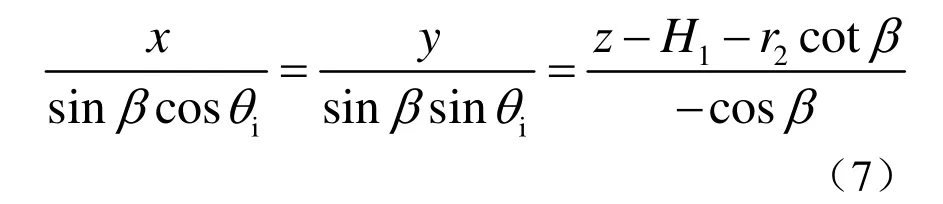
聯立式（5）和式(7)，可解出 mi(xmi,ymi,zmi)，它為θi的函數。θi的取值范圍為θ2≤θi≤180°。

2.4 求接口曲面和中性層曲線

設接口曲線上任意點為 m0(xm0,ym0,zm0)，其為角變量θ的函數，如圖 6所示。過m0點的接口曲面素線交支管軸線于d。a為該素線方向的單位矢量

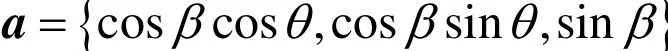
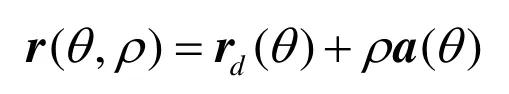
式中，0 ≤ θ ≤ π ，w-t≤ ρ ≤ w ，w為接口曲面素線由 d點到其與外皮交點的距離，w= ( H - zd)sin β + R2cos β。

令ρ= w - t 2，即得中性層曲線方程。

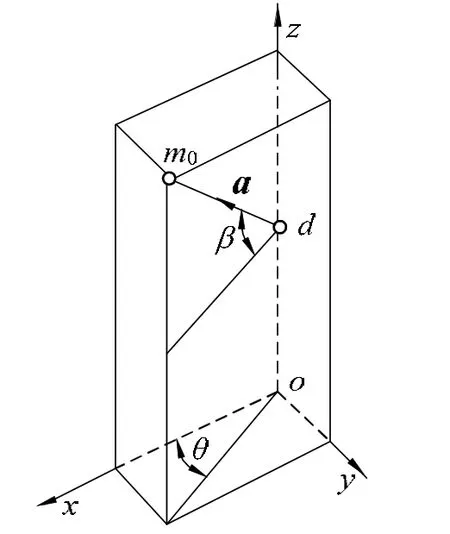
圖6 求接口曲面

3 接口幾何信息處理的數值方法

以UG平臺二次開發為工具[6]，基于數值方法，開發了接口幾何信息處理系統，系統具有很強的通用性，處理精度能夠滿足工程要求，該系統可作為鈑金展開CAD系統的應用模塊。

數值方法接口處理的原理如圖 7所示。首先用過支管軸線的平面（端口變量θ = 0°）進行截切，交得支管里、外皮素線和主管外皮交線（圖7(a)），延長兩素線與主管交線相交（圖7(b)、(c)、(d)），過兩交點分別作主管交線的切矢，若兩切矢斜率均為負值，則為里皮接觸（圖 7(b)）；若兩切矢斜率均為正值，則為外皮接觸（圖7(c)）。若兩切矢斜率符號改變，則為過渡區間（圖7(d)），這時需搜索切矢斜率為零的點，該點即為接觸點。在對一個截面處理后，增加θ 步長，再處理下一個截面。具體過程如圖8所示。

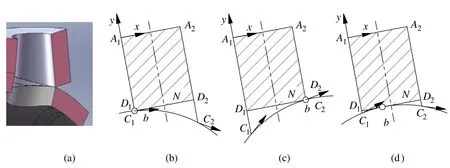
圖7 數值求解原理圖

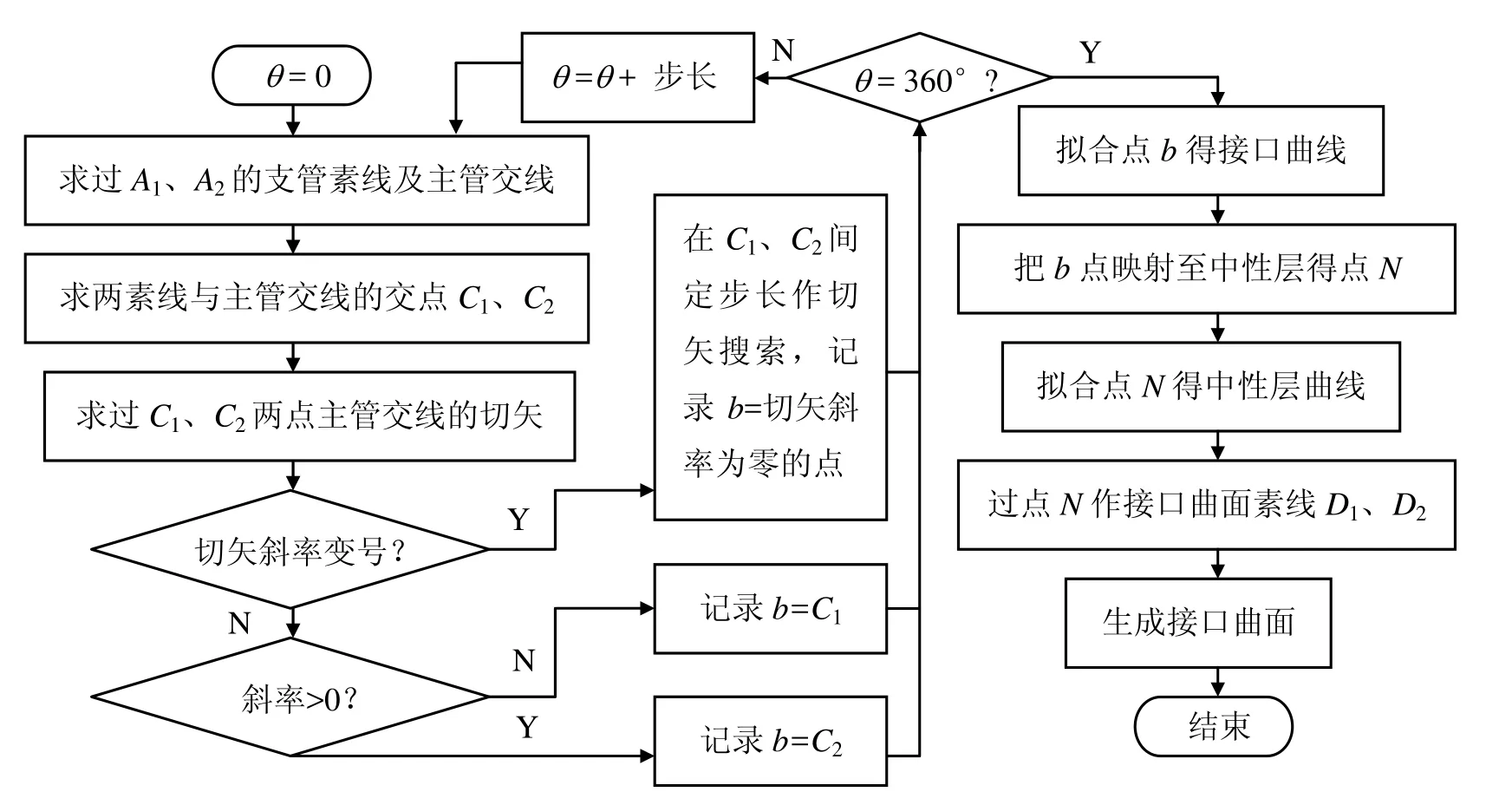
圖8 數值方法流程圖

圖9為接口幾何信息處理系統的應用舉例。左圖為圖形結構的選型菜單，中圖為根據計算結果所生成的具有真實接口形狀的構件模型，右圖為單獨顯示的接口曲線和中性層曲線。

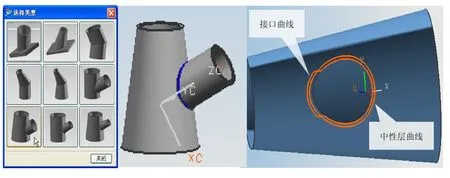
圖9 接口幾何信息處理系統應用

4 總結與展望

管類鈑金結構接口處的板厚處理在很大程度上影響著構件的制造與安裝精度。從圖解、解析和基于數值方法的系統開發幾方面研究鈑金行業最常用的管類鈑金結構接口處的板厚處理，實現了接口幾何信息的精確提取，其研究結果對于提高管類鈑金結構的產品質量、降低生產成本具有應用價值。

由于我國鈑金行業，特別是鈑金展開工藝長期處于基于經驗的傳統生產方式，鮮見優秀的鈑金展開軟件面世；一些軟件也由于板厚處理的缺陷只能限于對薄板構件的應用。通用性強、精度高、便于應用的鈑金展開軟件有著相當大的開發空間。

[1] 龐連軍,雷光明,趙 峰,等. 鈑金構件CAD系統研究與實現[J]. 機電產品開發與創新,2006,19(3):90-96.

[2] 王文昌. 鈑金展開技術手冊[M]. 沈陽: 東北工學院出版社,1991: 97-125.

[3] 毛 昕,李曉橋. 鈑金展開技術與應用實例[M]. 北京: 機械工業出版社,2007: 61-92.

[4] 樊文萱,宮述之,毛 昕,等. 鈑金展開技術手冊[M]. 北京: 北京出版社,1992: 59-91.

[5] 何 薇. 管類鈑金件參數化設計及其展開系統的開發與實現[D]. 沈陽: 東北大學,2008.

[6] 黃 翔,李迎光. UG應用開發教程與實例精解[M].北京: 清華大學出版社,2005: 13-80.