柔性接頭界面端角點應力奇異性①

安春利，任全彬，王鐵軍，趙桂平

(1.中國航天科技集團公司四院四十一所，西安 710025;2.西安交通大學，西安 710049)

柔性接頭界面端角點應力奇異性①

安春利1，任全彬1，王鐵軍2，趙桂平2

(1.中國航天科技集團公司四院四十一所，西安 710025;2.西安交通大學，西安 710049)

基于界面理論，建立了柔性接頭增強件、彈性件兩種結合材料形成的界面端角點附近奇異應力場方程，依據界面連續條件和自由邊界條件，得到了與奇異應力場關聯的特征值λ的線性齊次方程組，通過該方程組的求解和公式推導，給出了柔性接頭界面端角點附近含應力強度系數的奇異應力場和位移場;并根據特征值λ的取值范圍，獲得了應力奇異性消失的柔性接頭彈性件、增強件材料匹配和幾何形狀角選擇。選取柔性接頭常見工況，分別進行了角點附近奇異應力場解析解計算和有限元計算，驗證了解析解的正確性。

柔性接頭;應力奇異性;界面端角點;特征值;應力強度系數

0 引言

柔性接頭依靠粘接面傳遞載荷，粘接界面是高分子材料組成的界面相，該界面相將增強件和彈性件粘接在一起，由于彈性件、增強件為球形環狀薄片，導致在每層粘接面處存在界面端角點。柔性接頭漏氣破壞模式出現的主要原因:一是由粘接面某處脫粘或弱粘引起脫粘面的擴展而形成的漏氣通道;二是粘接面端部角點處存在應力奇異性。擺動中，角點部位率先形成脫粘源，隨之脫粘部位不斷擴大，形成貫穿性氣體通道，最終導致結構漏氣。漏氣的第一個原因屬于傳統意義上的界面強度問題，第二個原因則是由于設計參數不合理，致使粘接面角點的應力奇異性造成局部應力趨于無窮大，屬于界面力學范疇。工程研制中柔性接頭的破壞源，往往發起于界面端角點，因而柔性接頭粘接界面端角點，成為研究柔性接頭問題的一個焦點。

本文針對柔性接頭的第二個破壞原因，建立并求解了柔性接頭界面端角點的奇異應力場，根據與奇異應力相關的特征值λ取值范圍，研究了柔性接頭彈性件、增強件常見材料組合情況下的應力奇異性消失的幾何形狀角選擇。

1 結合材料定義及柔性接頭界面應力奇異性

1.1 結合材料定義

物性不同的異類材料，利用粘接、綁定等結合方法連接在一起、作為整體結構使用，稱為結合材料，由于是2種不同的材料結合在一起，材料參數共有4個彈性常數，即2個楊氏模量E或剪切模量，以及2個泊松比ν。對于諸多問題，這4個常數對結合材料應力應變的影響互相耦合，可用2個新的組合材料參數來描述，稱為 Dundurs參數［1-2］。

Dundurs參數:

式中E為彈性模量;ν為泊松比;下標為材料代號。

柔性接頭是由橡膠彈性件和金屬或復合材料增強件粘接而成的構件，符合結合材料的定義，結合材料的理論同樣適用于柔性接頭。

1.2 柔性接頭界面應力奇異性

柔性接頭的軸對稱界面角點和界面端模型見圖1。圖1中，z軸為柔性接頭對稱軸，通過幾何形狀角θ1、θ2和界面位置角θ0取值，可對柔性接頭的軸對稱界面端問題進行分析。

圖1 柔性接頭軸對稱界面端模型Fig.1 Axisymmetric model of interface corner in flexible joint

圖1 中(ρ、φ、z)為圓柱坐標系;ρ、z軸的取法見圖1;φ為圓周方向的角坐標;應力奇異點為O＇。

軸對稱問題，應力和位移可用2個調和函數來表示［3-4］:

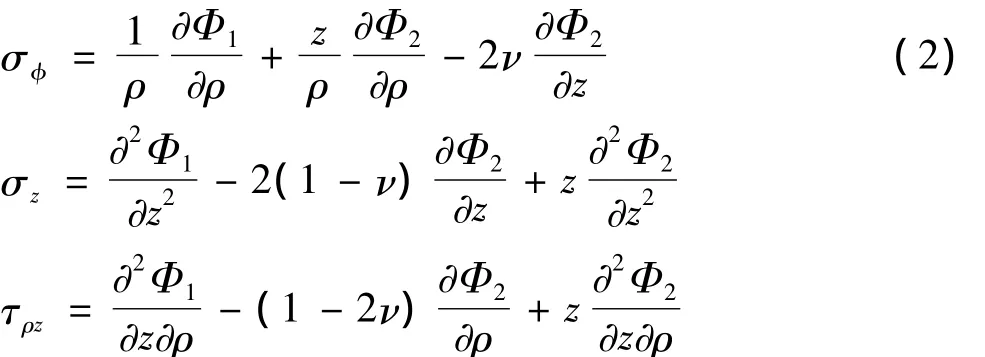
函數Φj為調和函數，滿足:

圖1中，界面連續條件和自由邊界條件可表示為

要確定應力和位移分量，必須確定2個調和函數具體的函數關系式，而2個調和函數可用含待定系數的級數型式給出，問題轉化為求調和函數級數形式的待定系數，界面連續條件與自由邊界條件與調和函數結合。經整理［5-7］，得到關于待定系數的線性齊次方程組，根據其有非零解的條件，其系數矩陣的行列式等于零，得到含特征值λ的特征方程，求得了特征值，可進一步得到非零的系數解，從而完整的給出奇異應力場和位移場。

針對圖1，特征方程為

其中，α、β 為 Dundurs參數(k=3-4ν)，即該特征方程式中的Dundurs參數與平面應變狀態下的Dundurs參數相同。

當給定結合材料及其界面端形狀后，λ為表征界面端應力場強度的應力奇異性指數，也為方程(4)的特征值，該方程因此被稱為界面端的特征方程。考慮到即使存在非零的常應力場，在界面端附近起支配作用的仍是奇異項。只考慮0＜Re(λ)＜1的特征值。

界面端角點附近的應力場(當r→0)可近似表述為

式中 ξ、η是特征值λ的實部、虛部;D是行列式。

2 柔接頭界面端角點附近應力場求解

方程(4)的求解過程，國內外學者已做了大量工作，本文不再多述。如果特征方程有多個特征值，則依據疊加原理求解，以兩個特征值λ1和λ2為例，界面端奇異點O附近在材料m(m=1，2)中的位移場和奇異應力場可分別表示為

式中K1與K2，fkm1(θ)與fkm2(θ)，Fkm1(θ)與Fkm2(θ)分別為對應于特征值λ1與λ2的應力強度系數、位移函數和應力函數;fkm1(θ)、fkm2(θ)、Fkm1(θ)、Fkm2(θ)是隨角度的變量，而K1、K2是定參數，需求解。

為確定結合材料界面端的應力強度系數K1、K2，需沿θ=θ0方向選擇2種已知應力分量σ(1)與σ(2)，則有

聯立求解組成的方程，可得到K1、K2。

3 柔性接頭界面端應力奇異性消除

一般情況下，方程(4)可能存在無窮多個根，界面端附近應力場的奇異性指數一般可由方程(4)所給出的根的最小實部Re(λ)表示，Re(λ)≤0時，界面端的位移趨于無窮大，沒有物理意義Re(λ)≥0時，界面端所對應的應力趨于零，是一個高階微量，λ=0時，對應的是一個剛體位移或常應力場。顯然，如果方程(4)僅存在Re(λ)≥1的根，界面端附近奇異應力場將會消失，考察方程(4)，當材料的(α、β)組合確定，通過Re(λ)≥0，并合理設定 λ 值，改變(θ1、θ2)值，就可找到應力奇異性消失的根和(θ1、θ2)組合。

4 算例

4.1 計算結果

某型號柔性接頭增強件材料30CrMnSiA，彈性件材料天然橡膠，Dundurs參數計算值 α=0.999，β=0.01，4個界面端角點位置、位移編號見圖2。

圖2 柔性接頭奇異點編號Fig.2 Singular point number of flexible joint

圖2中，角點1計算的位移和應力如下:

式中K是與工況相關的應力強度系數。

4.2 驗證

4.2.1 界面端角點附近奇異應力場驗證

某柔性接頭承受1.6 MPa水壓反向拉伸，界面承受拉剪應力，界面應力無法實測，本文采用具有強健計算功能和廣泛模擬性能的ABAQUS有限元軟件，計算出柔性接頭粘接界面角點附近的應力。然后，以有限元法計算的應力值來驗證本文給出的解析解計算結果的正確性，柔性接頭反向水壓拉伸工況有限元網格劃分時，在考慮計算機能力的前提下，分別取單元長度與r=5×10-1mm比值為1、5、10進行了計算，并進行了比較，計算結果見圖3、圖4。

圖3 彈性件軸向應力Fig.3 Axisymmetric stress of elastomer

針對奇異點1，選取r=5×10-1mm，以有限元計算的σr為基準，計算得到應力強度系數K=1.35×10-3，依次應用解析解推得r=5×10-1mm其他位置的σr值，并與有限元結果比較，見表1。

圖4 增強件Mises應力Fig.4 Mises stress of reinforcement

表1 某柔性接頭奇異點1，r=5×10－1mm處解析解與有限元解比較Table 1 Theoretical and FEM calculation comparison in singular point 1，r=5 ×10－1mm

反向水壓工況下徑向應力理論解與有限元計算結果比較表明，最大誤差為13%，且應力趨勢一致，證明柔性接頭粘接界面角點的應力理論解基本正確，可用來計算柔性接頭粘接界面角點附近應力和指導柔性接頭參數設計。

4.2.2 界面端角點應力奇異性消失幾何形狀角組合研究

根據某型號柔性接頭的結構尺寸，依次將增強件材料換為30CrMnSiA、鈦合金、鋁合金、炭布，彈性件材料模量在 0.1、1.0、2.0 MPa 之間選擇，分析了平面應變和平面應力狀態下的應力奇異性消失組合，結果見圖5、圖6及表2。

圖5 平面應變組合角曲線Fig.5 Change of angle in planar strain

圖6 平面應力組合角曲線Fig.5 Change of angle in planar stress

結果表明，采用曲線下方的任意角度組合，都可消除柔性接頭界面端角點的應力奇異性，但采用不同的角度組合，對界面角點附近的應力分布規律的影響是不同的。同時還應注意，對于柔性接頭，彈性件材料的配方基體是橡膠，其彈性模量變化不大;而對于增強件，材料為炭布/酚醛時，其應力奇異性消除的角度組合范圍較寬。因此，在能滿足增強件強度要求的前提下，應盡量選用非金屬復合材料，以減少粘接界面角點的應力奇異性。

對于鋼和彈性件粘接，應力奇異性消失的組合角度范圍相對較窄，但鋼和彈性件的粘接，卻是一種常用結構方式。圖6顯示θ1在20°范圍內時，θ2可取137°之內的值，當 θ2在 55°以下時，θ1取值方位較廣，θ1、θ2在這些范圍內取值，界面端角點均無應力奇異性產生。

5 結論

建立了適用于固體火箭發動機噴管柔性接頭界面端角點附近奇異應力和位移的理論計算公式，理論公式結果表明，應力和位移奇異性與彈性件、增強件材料組合和幾何形狀有關，柔性接頭的結構失效，界面端角點的應力奇異性是一個重要的誘導因素;通過不同材料匹配和幾何形狀角選擇，可有效消除角點應力和位移的奇異性;同時，界面角點附近的奇異應力場與柔性接頭所受載荷緊密相關。柔性接頭反向水壓工況的有限元仿真結果，驗證了理論公式解的正確性。

［1］許金泉.界面力學［M］.北京:科學出版社，2006.

［2］Bogy D B.Edge-bonded dissimilar orthogonal elastic wedges under normal and shea loading［J］.Journal of Applied Mechanics，1968，35:460-466.

［3］劉一華，許金泉，丁皓江.軸對稱界面端的應力奇異性［J］.浙江大學學報.1998，32:307-314.

［4］Liu Y H，Xu J Q，Ding H J.Order of singularity and singular stress field about an axisymmetric interface corner in three dimensional isotropic elasticity［J］.Int.J.Solids Struct.，1999，36:4425-4445.

［5］Dundurs J.Discussion of edge boned dissimilliar orthogonal elastic wedges under normal and shear loading［J］.Journal of Applied Mechanics，1969，36:650-652.

［6］Dundurs J.Effect of elastic constants on stress in a composite under plane deformations［J］.Journal of Composite Materials，1967(1):310-322.

［7］Demsey J P ，Sinclair G B.On the stress singularities in the plane elasticity of the composite wedge［J］.Journal of Elasticity，1979，9:373-391.

Stress singularity of flexible joint in combined material interface corner

AN Chun-li1，REN Quan-bin1，WANG Tie-jun2，ZHAO Gui-ping2
(1.The 41st Institute of the Fourth Academy of CASC，Xi＇an 710025，China;2.Xi＇an Jiaotong University，Xi＇an 710049，China)

On basis of the mechanics of interface，singular stress field of interface corner created by reinforcement and elastomer of flexible joint was established.According to interface continuous condition and free boundary condition，the linear equation group of characteristic value λ which is related to the singular stress field was obtained.Then，singular stress field and displacement field which include stress intensity coefficient in interface corner of flexible joint were found through solving equation group and deducing formula.At the same time，based on the range of λ value，the selection of reinforcement and elastomer as well as geometrical angle with the stress singularity disappearing were presented.The results of singular stress field gained from calculation and finite element method verify the correctness of the analytical solution in this report.

flexible joint;stress singularity;interface corner;characteristic value;stress intensity coefficient

V435

A

1006-2793(2012)03-0391-05

2011-11-07;

2012-03-09。

安春利(1971—)，男，博士，主要從事固體火箭發動機的噴管研究。

(編輯:薛永利)