一種改進的自適應遺傳算法

文/劉曉霞 竇明鑫

（1.河北金融學院；2.中國地質大學長城學院 河北·保定）

引言

遺傳算法（GA）由美國Michigan大學的Holland教授于1975年首先提出，后經De Jong、GoldBerg等人改進推廣，廣泛應用于各類問題。它是一種模擬自然界生物進化過程與機制的全局概率優化搜索方法。

早期遺傳算法在進化過程中易出現早熟收斂和局部收斂性差等問題，為了克服上述問題，人們提出了多種改進算法。本文對自適應算法進行改進，算法中不僅交叉和變異概率是自適應的，而且構造了一種自適應的適應度函數，以便更好地進行復制、交叉、變異操作，同時結合實數編碼精度高、搜索范圍大和二進制編碼的收斂速度快、變異操作易實現的特點，算法還采用了實數與二進制編碼相結合的方式，在防止早熟的同時還能提高全局搜索能力，最后利用改進算法進行仿真實驗，結果表明本算法具有收斂概率高和平均收斂代數少的優點。

一、改進的遺傳算法

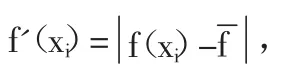
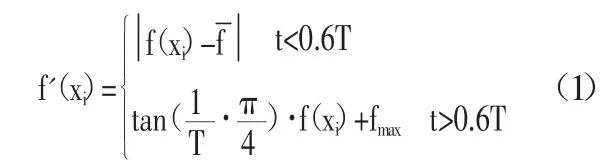
其中，fmax為上一代最優解所對應的函數值，t為當前代數，T為預先設置好的最大迭代次數。

2、格雷碼周期變異。由于二進制變異容易控制，可以避免考慮實數變異涉及的變異方向，所以本文在變異操作中采用二進制格雷編碼，格雷編碼的定義見（2）式，

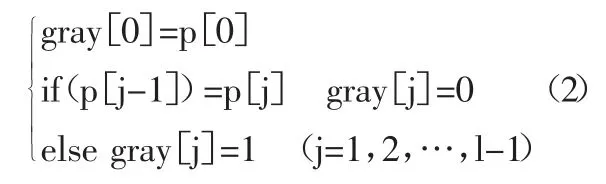
其中，p為原二進制編碼，l為編碼長度。格雷編碼不僅具有良好的局部搜索能力，還能克服二進制編碼Hamming懸崖，之后將變異概率設定成一個周期性變化的函數，見（3）式：

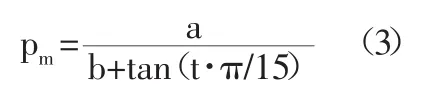
其中，a，b是待定值，此函數在一個周期內是單調遞減的，在進化后期種群趨于穩定時，降低選擇壓的同時應該采取大概率變異，保持種群的多樣性，防止陷入局部解。經測試，當a=3，b=19時算法性能較好。

二、算法步驟

Step1 采用實數編碼產生初始種群，在函數定義域內按照均勻分布隨機產生n個個體，｛xi｝（1，2，…n）設定最大進化代數設為T。

Step3 根據每個個體的適應度，采用比例選擇法。通過這種適應度轉換，使得在進化前期原本函數值小的個體將有更大的概率被選擇，保持了種群的多樣性。

Step4 按照概率pc在種群中隨機選擇父代個體進行交叉操作。

Step5 首先依據變異概率pm選定變異個體，然后利用格雷碼周期變異操作進行編碼、變異、最后解碼。

Step6 最優保存策略。本文將最優保存策略算法做如下修改：第一步，計算每個個體的函數值，然后排序，找出最優解，最差解；第二步，若上一代最優解的函數值比當前最優解的函數值大，則用上一代的最優解替換當前最優解；若上一代的最優解函數值小，則用上一代的最優解替換當前中的最差解。這樣，基于Markov鏈的數學理論分析表明，保留最優個體策略的遺傳算法就能夠以概率1收斂于最優解。

Step7 滿足迭代次數即停止，否則代數加1，轉入Step2。

三、仿真試驗

1、測試函數。選取文獻[3、6、7]的測試函數為：

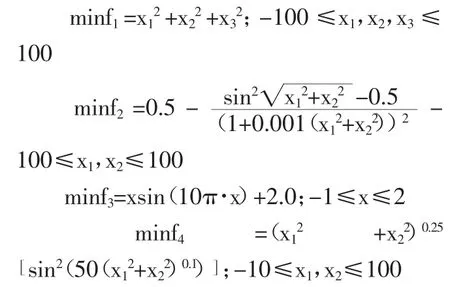
其中，f1為單峰二次函數，當（x1+x2+x3）＝（0，0，0）時有全局最小值 0；f2有無數個局部最大值，只有一個全局最大點（0，0），最大值為1；f3是一維連續且含三角函數的多峰函數，當x=1.8505時，全局最大值為 3.8503；f4是 Schaffer函數，當（x1，x2）=（0，0）時有全局最小值 0。

2、測試結果對比分析。用本文算法同基本遺傳算法和自適應遺傳算法進行比較，其中取種群規模m=200，基本遺傳算法的交叉概率pc=0.85和變異概率pm=0.1，自適應遺傳算法的交叉概率和變異概率分別為：

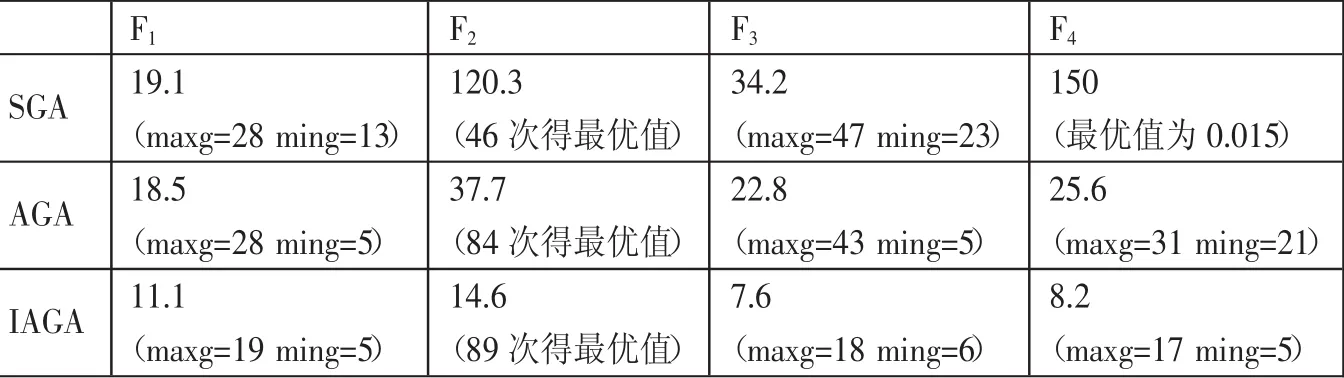
表1 三種算法對測試函數的運行結果

其中，pc1=0.85，pc2=0.65，pm1=0.15，pm2=0.05，f'為兩個要交叉個體適應度大的個體適應度值，最大迭代次數設為T＝150，對各測試函數分別獨立運行100次得到表 1。（表 1）

通過實驗表明，本文的算法在對函數f1、f3、f4的測試中，達到最優值的收斂代數明顯減少，得到了令人滿意的效果，對函數f2的測試中雖然本文算法提高了算法的收斂概率，同時收斂的代數也明顯減少，所以本文的算法在減少收斂代數方面和提高收斂概率方面是具有優越性的。

四、結束語

本文提出改進的適應度函數，使得在進化初期一些函數值差的個體也能有更高的概率參與到選擇、交叉、變異操作中，保存了種群的多樣性，同時在自適應交叉的過程也采用了新的方法，使得在避免“近親繁殖”的基礎上擴大了搜索范圍，整個算法結合實數編碼的全局能力強和格雷碼局部收斂能力強的兩個特點，在算法中使用了實數編碼與格雷編碼相結合的方法，使得收斂的迭代次數明顯減小。雖然采用格雷編碼會導致算法收斂速度慢，但是明顯降低了不收斂的次數，大大提高了算法收斂速度和收斂概率，使本文算法具有較高的計算效率。

[1]王力，侯燕玲.基于遺傳算法通用試題庫系統研究[J].微計算機信息，2008.5.

[2]李敏強，寇紀淞，林丹等.遺傳算法的基本理論與應用[M].北京：科學出版社，2004.

[3]楊曉華，陸桂華，酈建強.解非線性極大極小問題的格雷碼加速遺傳算法[J].河海大學學報，2003.31.1.

[4]魏平，熊偉清.一種改進的實數編碼遺傳算法[J].計算機應用研究，2004.21.9.

[5]王小平，曹立明.遺傳算法——理論、應用與軟件實現[M].西安：西安交通大學出版社，2002.