基于姿態參數切換的四元數快速傳遞對準算法

周衛東， 吉宇人， 喬相偉

(哈爾濱工程大學自動化學院，黑龍江哈爾濱150001)

0 引言

Kain J E提出的速度+姿態匹配算法是目前最為常用的傳遞對準算法之一［1］，其推導的快速傳遞對準模型在小角條件下進行了合理的線性化處理。在艦載武器的傳遞對準中，粗對準階段完成之后，主子慣導間的相對誤差依然較大，無法進行線性簡化(比如艦載機與載艦的方位失準角往往為一個大角)。由于歐拉角法具有簡單、直觀的幾何意義，因此基于歐拉角的非線性誤差模型得到了較多的應用［2］。但在大角度的姿態描述中，歐拉角法會受到奇異性及超越函數的限制。與此相比，四元數法具有非奇異性、計算量小、對大角度旋轉描述更精確等優點，因此被越來越多地應用于傳遞對準研究中［3－4］。同時，建立四元數誤差模型也可使濾波器直接采用慣導設備即時修正得到的姿態四元數，因此精確度更高。

與之對應的非線性四元數濾波算法主要有四元數擴展卡爾曼濾波算法(quaternion extended Kalman filter，QEKF)和四元數無跡卡爾曼濾波(quaternion unsented Kalman filter，QUKF)。文獻［5］將 EKF 算法與四元數結合，利用誤差四元數的量測更新保證后驗姿態四元數的規范性。但EKF算法存在高階截斷誤差及雅克比矩陣求解的限制，而基于sigma點選取的UKF算法在保持與EKF計算量相當的同時，其濾波精確度達到泰勒展開式的二階［6］，因此將其與四元數結合可在保證實時性的前提下，進一步提高濾波精確度［7－11］。但在四元數UKF算法中，需要解決四元數sigma點選取及加權求和的問題。針對前一個問題，文獻［8］提出取四元數向量部分參與sigma點計算，再通過單位化約束得到標量的方法。而針對加權求和問題，文獻［9］提出構建代價函數的方法，文獻［10］通過奇異值分解進行計算，但都受到計算量較大的限制。對此，文獻［11］提出了利用修正羅德里格斯參數(modified rodriguez parameters，MRPs)與四元數相互轉換以保證四元數規范性的方法。基于該思路，將兩種參數間的映射關系引入四元數UKF算法中，利用MRPS較低的轉換復雜度及其不受單位化限制的特性，解決四元數UKF算法中的加權求和問題，從而使其計算量較其他四元數UKF算法更低。

針對艦載武器中大失準角的快速傳遞對準問題，在建立四元數誤差模型的基礎上，利用姿態參數轉換的方法解決四元數的加權求和問題，并對四元數sigma點的求取及誤差方差陣進行推導。

1 基于乘性四元數的誤差模型

1.1 姿態誤差模型

首先對推導過程中將要用到的符號變量進行定義:n為導航坐標系;e為地球坐標系;s*為子慣導系統解算的載體坐標系;s為子慣導系統所在的真實載體坐標系;m為主慣導系統解算的載體坐標系;ψm為s*系與m系之間的量測失準角;ψa為s系與m系之間的實際失準角;為從m系到s系的方向余弦矩陣;為從m系到n系的旋轉角速度在m系上的投影，其他角速度定義與此類似;rn為桿臂在n系上的投影;為加速度計隨機偏置誤差為陀螺儀隨機偏置誤差;為從m系到s系的乘性四元數為其轉置;為從m系到s*系的乘性四元數為其轉置。

快速傳遞對準算法引入了相對失準角的概念，即s*系與m系之間的量測失準角ψm和s系與m系之間的實際失準角ψa。該算法在由Kain J E首次提出時，其姿態誤差模型是在小失準角的假設下推導建立的。在艦載武器的實際應用中，經常會出現初始誤差角為大角度的情況。此時，基于歐拉角的非線性姿態誤差模型［1，3］為

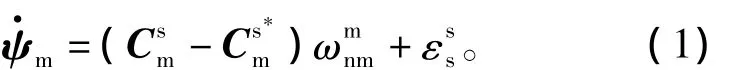
四元數法作為一種非奇異姿態描述方式，其定義為

式中:q0為四元數Q的標量部分;ρ為四元數Q的向量部分。將向量與看作零標量的四元數，其四元數乘法［12］表示為

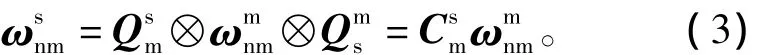
為使推導清晰，定義向量自動轉化為零標量的四元數后再進行四元數乘法運算，其結果自動轉回向量形式。根據式(3)，式(1)可寫為

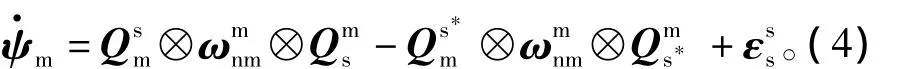
再根據四元數微分方程及角速度定義式，即

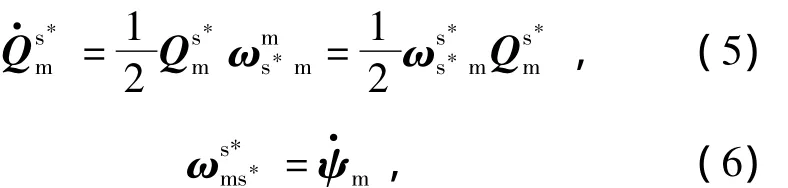
得到基于乘性四元數的非線性姿態誤差模型為

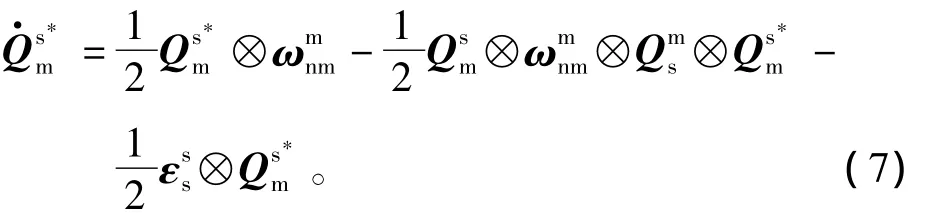
1.2 速度誤差模型

考慮桿臂效應的速度誤差模型為

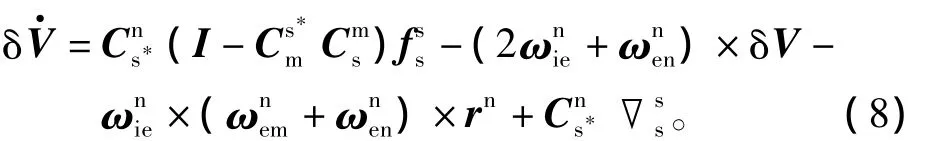
式中:δV為主、子慣導間的速度誤差。根據四元數的相繼轉動性［12］，即

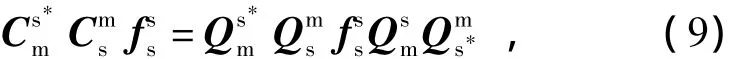
得到基于乘性四元數的速度誤差模型為

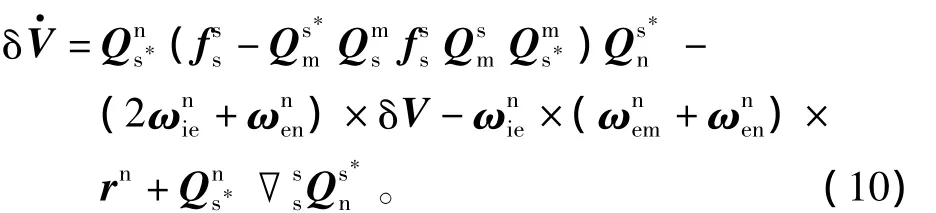
1.3 量測方程

針對狀態方程中過程噪聲為乘性噪聲的情況，將過程噪聲擴維至狀態變量中。取系統狀態為

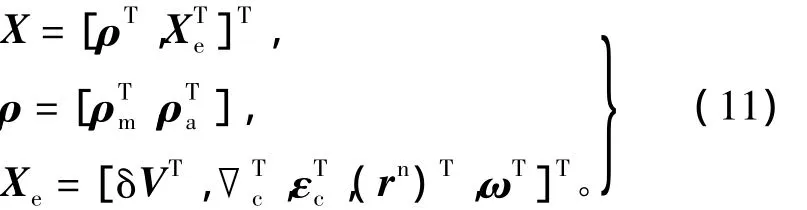
式中:Xe為擴維后的非四元數部分;2c和εc分別為加速度計和陀螺儀的常值偏置和常值漂移;ω為過程噪聲;ρm和ρa分別為量測失準角及實際失準角的等效姿態四元數的向量部分，滿足

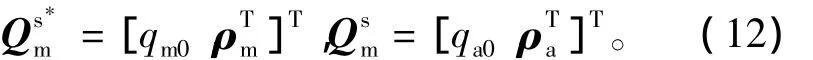
快速傳遞對準在觀測方程中選擇主子慣導間的相對姿態與速度誤差作為量測量，其量測方程為

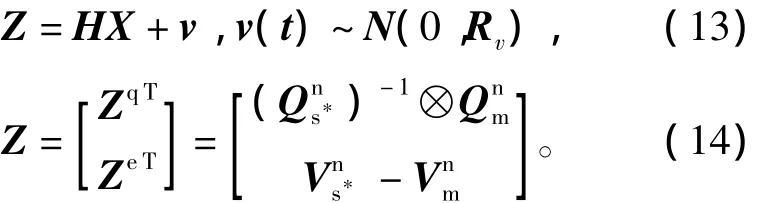
2 基于姿態參數轉換的四元數UKF算法設計

2.1 姿態參數轉換方法

在采用四元數法描述三維空間中剛體的定點轉動時，其4個元素并不相互獨立，因此需要對獲得的四元數進行規范化運算以保持其單位性，即

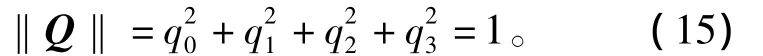
在四元數UKF算法中，sigma點經非線性函數傳播后需進行加權求和得到后驗均值。而姿態四元數作為描述剛體一次旋轉的旋轉矢量，直接進行四則運算意義下的計算將破壞均值四元數的規范性。對此，本文基于姿態參數轉換原理，對四元數的加權求和公式進行推導。首先給出另一種姿態參數—修正羅德里格斯參數(MRPs)的定義及其與姿態四元數間的相互轉換關系。MRPs是一種基于剛體定點轉動的3參數姿態描述方法，其各個分量之間相互獨立，因此并不受到規范化的限制。其定義為

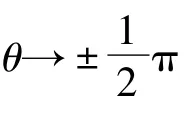
MRPs轉化為姿態四元數的公式為

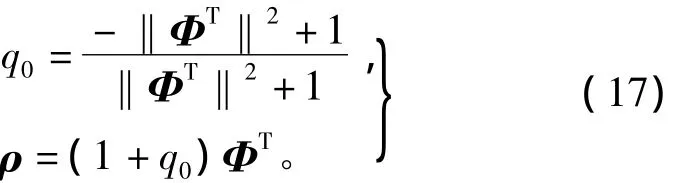
式中，Φ為MRPs，姿態四元數轉化為MRPs的公式為

2.2 姿態四元數加權求和算法

對其加權求和，得到均值MRPs為

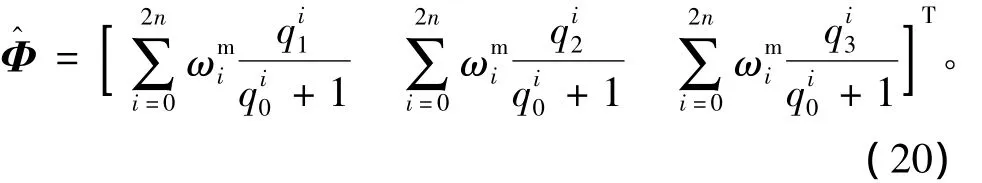
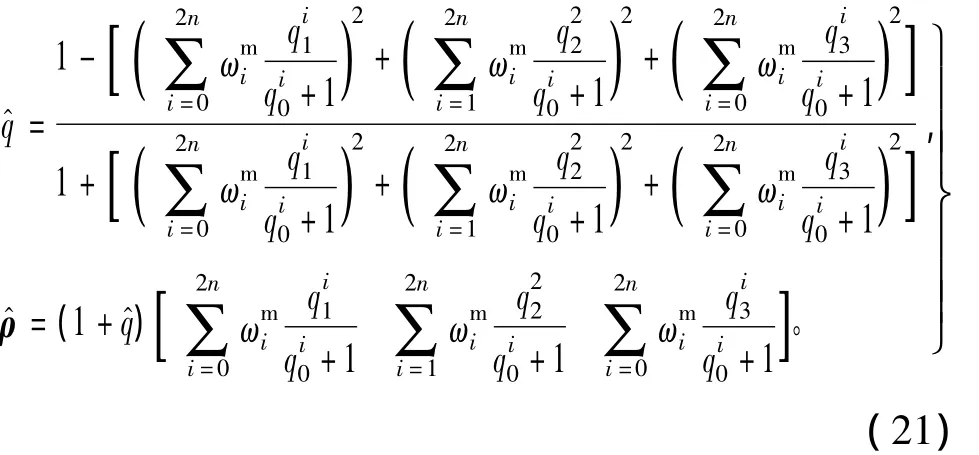
2.3 基于單位四元數的sigma點選取

在四元數UKF算法中，選取sigma點時需保證其四元數部分為單位四元數。對此，文獻［11］提出只取四元數向量部分參與sigma點計算，之后再通過單位化約束得到標量部分的方法。其計算步驟為

1)計算擾動sigma點，即

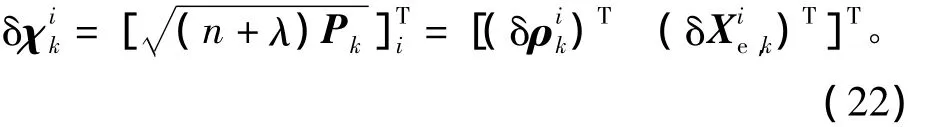
式中:Pk為狀態誤差方差陣;n為系統狀態維數;為方陣第i行的轉置;λ為尺度參數;為擾動sigma點中的四元數向量部分;為 非四元 數部分。

2)根據單位化約束計算標量部分，即

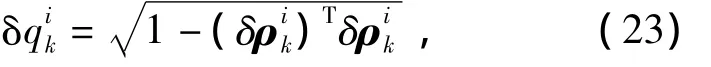
從而得到單位擾動四元數為

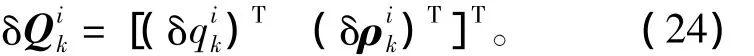
sigma點的計算公式為

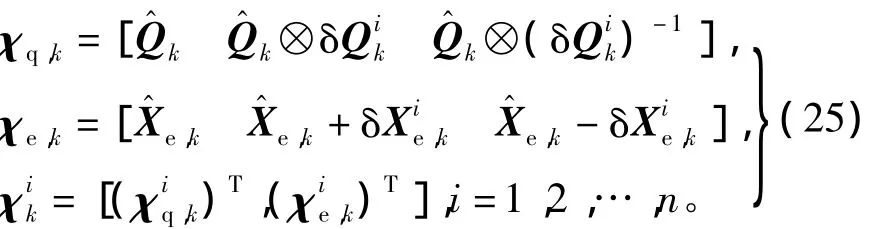
式中:χq，k為 sigma 點的四元數部分;χe，k為非四元數部分。

2.4 基于單位四元數的誤差方差陣計算

在四元數法中，兩次旋轉之差一般通過右乘旋轉四元數的逆實現。因此在計算誤差方差陣時，需要與非四元數部分區別實行。定義均值四元數與擾動四元數之差為

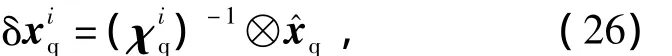
非四元數部分之差為

從而得到自協方差公式為

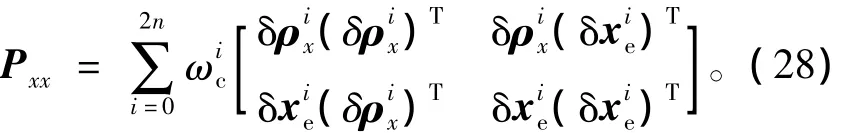
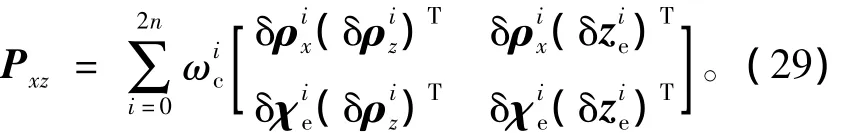
2.5 四元數UKF濾波算法

根據前4節的推導，得到基于姿態參數轉換的四元數UKF濾波算法流程如下。

設定狀態初值為

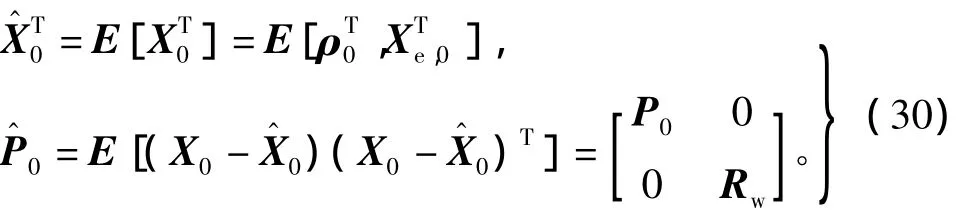
式中:P0為非噪聲部分的誤差方差陣，根據2.4節的推導進行計算，為使表述清晰，將采用經典UKF;算法的表達式，具體方法則按前4節推導進行操作;Rw為過程噪聲方差陣。

1)sigma點選取與權值計算

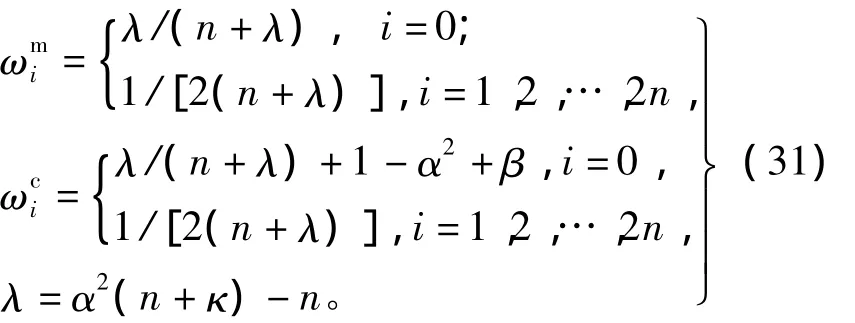
2)時間更新

sigma點通過非線性四元數誤差狀態方程傳播得到，即

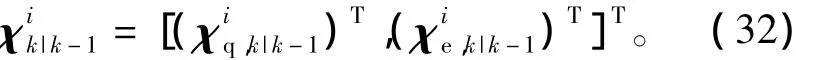
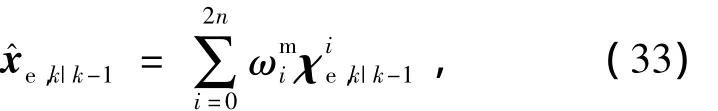
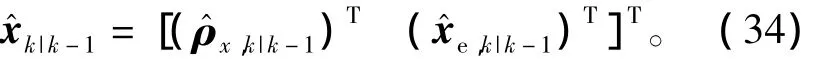
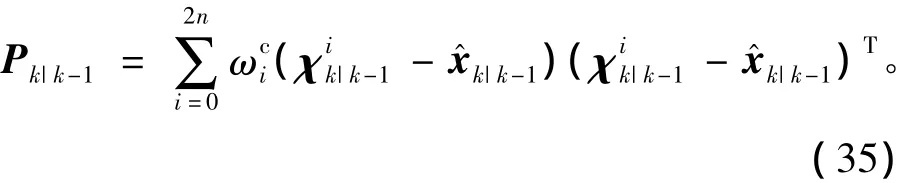
3)量測更新

sigma點通過四元數量測方程傳播得到，即

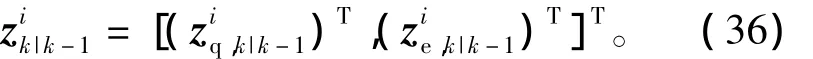
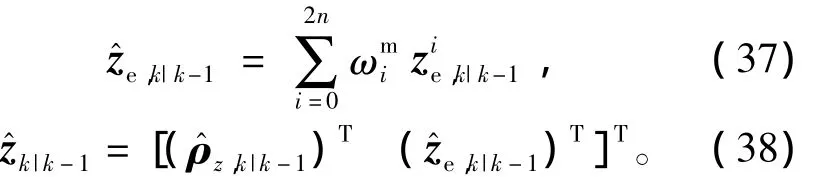
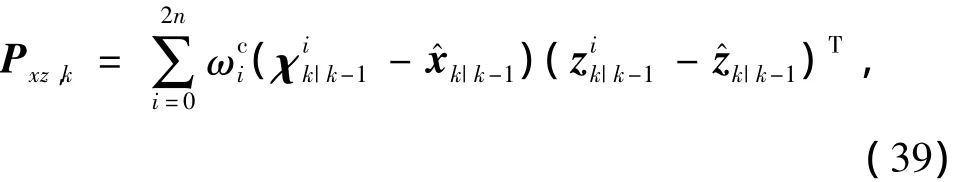
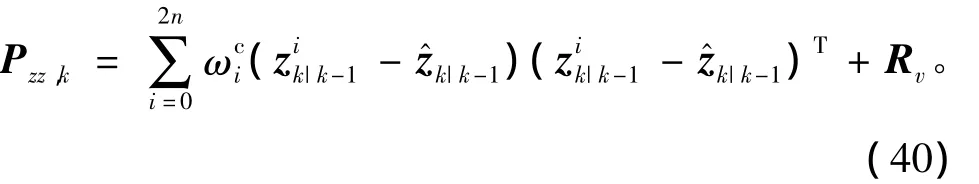
4)狀態更新

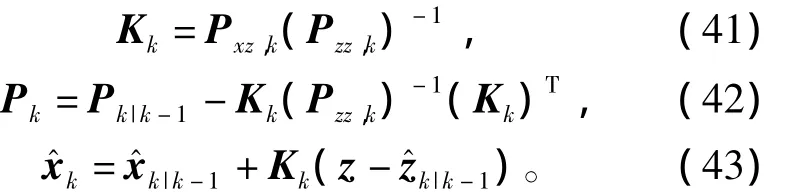
3 仿真分析

以艦載武器的快速傳遞對準為例，對不同姿態參數下的非線性誤差模型及相應的非線性濾波算法進行仿真對比。在風浪及減搖鰭作用下艦船產生的搖擺運動模型為

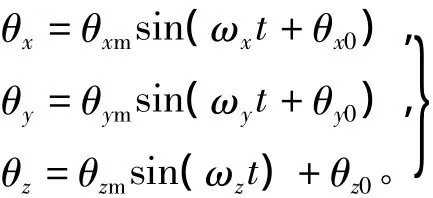
搖擺幅度為:θxm=5°;θym=4°;θzm=2°。搖擺頻率為:ωx=0.15 rad/s;ωy=0.1 rad/s;ωz=0.06 rad/s。初始角為:θx0=0°;θy0=0°;θz0=45°。

艦船的對地運動模型為

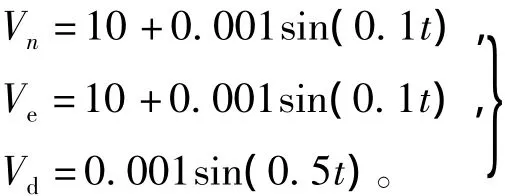
子慣導系統陀螺常值漂移取為0.1°/h，隨機漂移取為0.01°/h，加速度計零偏取為10－3g，隨機偏差為10－4g。桿臂取為(15 15 5)，單位為m;水平方向上的兩個姿態失準角分別為ψx=20′，ψy=40′，航向失準角為ψz=10°。系統狀態非四元數部分初始值設為0，四元數部分設為［1，0，0，0］T;設 INS 解算周期為0.01 s，濾波周期為0.5 s，仿真時間為50 s。

方案1采用歐拉角模型和經典UKF濾波算法，方案2采用四元數模型和基于奇異值分解的四元數UKF濾波算法，方案3采用四元數模型和基于姿態參數切換的四元數UKF濾波算法。

3個方案對姿態失準角的估計誤差如圖1～圖3所示。

圖1和圖2分別為3種方案下水平方向姿態失準角的估計誤差曲線圖。從圖中可以看出，3種方案在非線性程度不高的條件下都可以保持較高的估計精確度及收斂速度，在10 s后都達到穩定。圖3為航向失準角的估計誤差曲線圖。基于歐拉角法的方案一出現較大偏差，精確度明顯降低。方案2采用基于奇異值分解的四元數UKF算法，由于受到算法復雜度的限制，其收斂速度較慢，但仍保持較高的估計精確度。方案3的收斂速度略慢于方案1，但比方案2快，這主要歸因于四元數濾波算法的種種約束性條件在一定程度上提高了算法的運算量，但姿態參數適中的轉換復雜度及四元數自身較小的計算量使得方案2依然能夠滿足實時性要求，而四元數法的應用則使其在非線性提高時依然能夠保持較高的估計精確度，其對航向失準角的估計精確度較方案1提高了4倍以上。表1為3種方案的估計精確度比較。

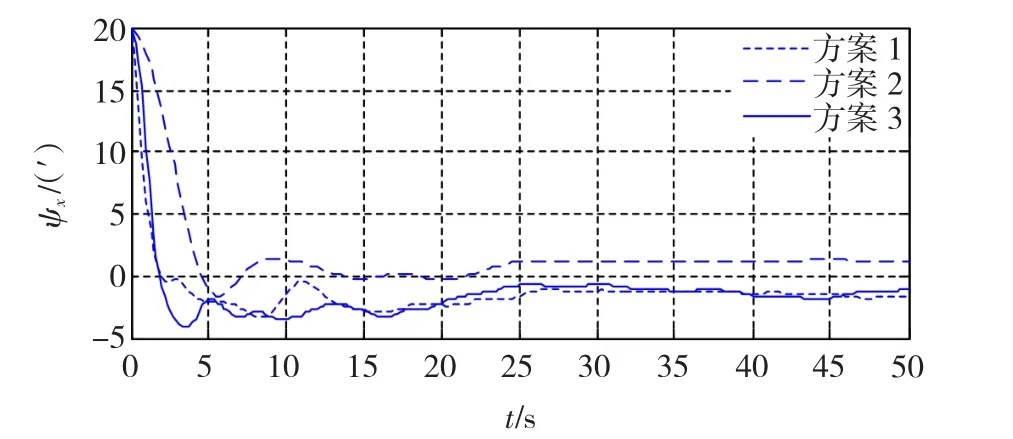
圖1 縱搖失準角估計誤差ψxFig.1 Estimation error of pitching misalignment ψx

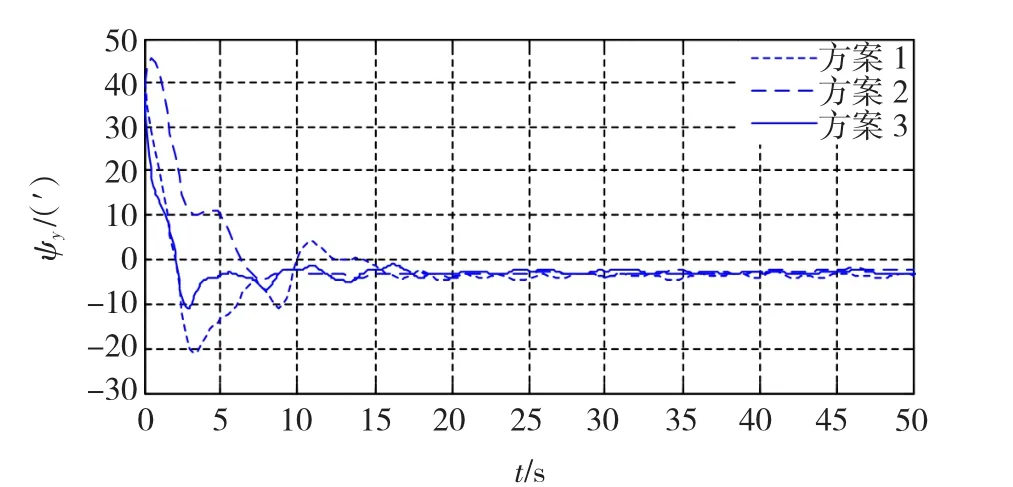
圖2 橫搖失準角估計誤差ψyFig.2 Estimation error of rolling misalignment ψy

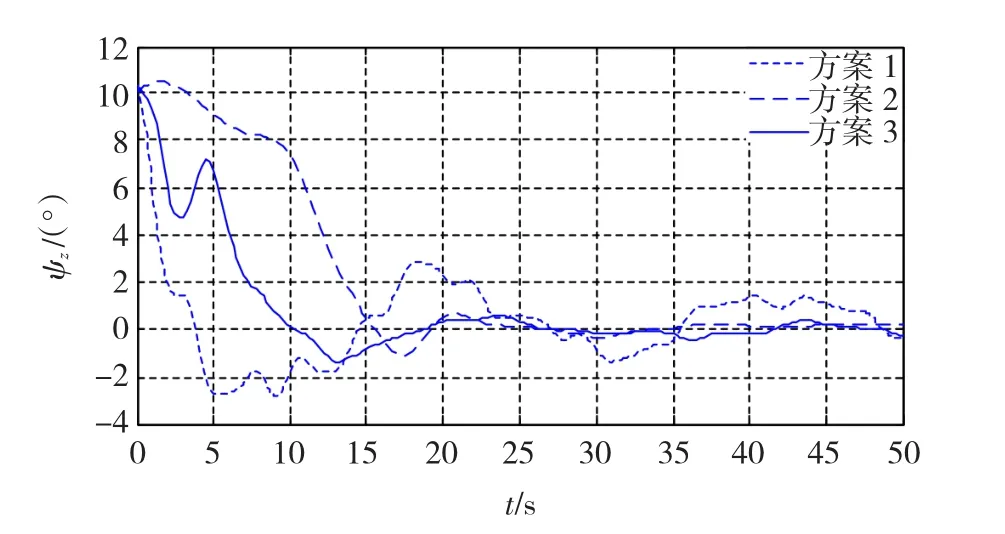
圖3 航向失準角估計誤差ψzFig.3 Estimation error of heading misalignment ψz

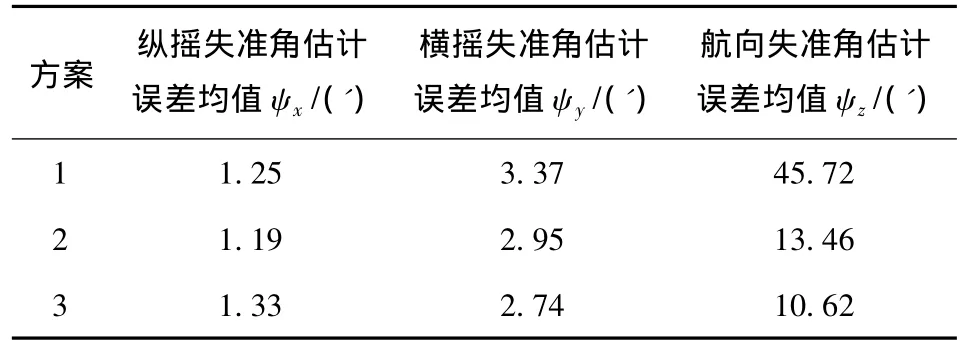
表1 3種方案的估計精確度比較Table 1 Comparison of estimation accuracy of 3 schemes

4 結語

本文利用修正羅德里格斯參數與四元數相互轉化的方法對四元數加權求和公式進行了推導，克服了UKF算法中一步預測均值的四參數規范化限制。同時對擾動sigma點中四元數部分的單位化問題及誤差方差計算問題給出了相應的解決方法。仿真結果表明，該算法與傳統UKF算法相比，對大方位失準角具有更高的濾波精確度。而與基于奇異值分解的四元數UKF算法相比，其實時性更好，適用于主子慣導間姿態失準角較大的快速傳遞對準技術。

［1］ KAIN J E，CLOUTIER J R.Rapid transfer alignment for tactical weapon application［C］//AIAA Guidance，Navigation and Control Conference，Auguest 14 － 16，1989，Boston，USA.1989:1290－1300.

［2］ 譚紅力，黃新生，岳冬雪.捷聯慣導大失準角誤差模型在快速傳遞對準中的應用［J］.國防科技大學學報，2008，30(6):19－23.

TAN Hongli，HUANG Xinsheng，YUE Dongxue.Rapid transfer alignment based on large misalignment SINS error model［J］.Journal of National University of Defense Technology，2008，30(6):19－23.

［3］ 熊芝蘭，郝燕玲，孫楓.基于四元數的慣導系統快速匹配對準算法［J］.哈爾濱工程大學學報，2008，29(1):28 －34.

XIONG Zhilan，HAO Yanling，SUN Feng.Rapid matching alignment algorithm of inertial navigation system based on quaternion［J］.Journal of Harbin Engineering University，2008，29(1):28－34.

［4］ 戴邵武，李娟.一種快速傳遞對準方法的誤差模型研究［J］.宇航學報，2009，30(3):942 －946.

DAI Shaowu，LI Juan.Study of rapid transfer alignment error model［J］.Journal of Astronautics，2009，30(3):942 －946.

［5］ LEFFERTS E J，MARKELY F L，SHUSTER M D.Kalman filtering for attitude estimation［J］.Journal of Guidance，Control and Dynamics，1982，5(5):417 －429.

［6］ JULIER S J，UHLMANN J K.Unscented filtering and nonlinear estimation［J］.Proceeding of the IEEE，2004，92(3):401－422.

［7］ CHOUKROUN D，BAR-ITZHACK I Y，OSHMAN Y.Novel quaternion Kalman filter［J］.Transactions on Aerospace and Electronic Systems，2006，42，(1):174 －190.

［8］ HENZEH LEEGHIM，YOONHYUK CHOI.Uncorrelated unscented filtering for spacecraft attitude determination［J］.Journal of Acta Astronautica，2010，67(2):135－144.

［9］ OSHMAN Y，CARMI A.Attitude estimation from vector observations using genetic algorithm embedded quaternion particle filter［J］.Journal of Guidance，Control and Dynamics，2006，29(4):879－891.

［10］ MARKLEY F L，CHENG Y，CRASSIDIS J L，et al.Averaging quaternion ［J］.Journal of Guidance，Control and Dynamics，2007，30(4):1193－1197.

［11］ CRASSIDIS J L，MARKLEY F L.Unscented filtering for spacecraft attitude estimation［J］.Journal of Guidance，Control and Dynamics，2003，26(4):536 －542.

［12］ 秦永元.慣性導航［M］.北京:科學出版社，2006:305－381.