耦合電抗器在并聯型三相并網逆變器中的應用

李瑞， 徐殿國， 徐壯， 蘇勛文

(哈爾濱工業大學電氣工程及自動化學院，黑龍江哈爾濱150001)

0 引言

隨著人們環保意識的增強及能源的日益緊缺，以風能、太陽能等為代表的新能源產業得到了長足的發展［1－2］。為了將由風能、太陽能等轉換而來的電能輸送到電網，通常需要由并網逆變器將其轉換為幅值、頻率、相位與電網相一致的電能，從而實現系統的并網運行［3－6］。為了提高并網逆變器的功率等級，同時降低生產成本，并提高系統可靠性，逆變器的并聯運行得到了廣泛關注［7－10］，為解決其中存在的環流問題，國內外學者進行了深入研究［11－12］。

傳統上，通常采用交流側使用隔離變壓器方案或適當軟件方案以抑制零序環流。文獻［13］將多個結構相同的變換器并聯使用，交流側通過隔離變壓器將各變換器的輸入隔離起來，提高了變換器的功率等級，消除了零序環流問題，但隔離變壓器的使用大大增加了系統的體積、重量和成本。文獻［14］提出了并聯型永磁直驅風電變流器拓撲結構，交流側省去了隔離變壓器，同時設計了零序環流器控制器，抑制了零序環流，大大提高了風電變流器的功率等級，但由于零序環流阻抗較小，因此零序環流問題解決起來難度相對較大，此外，零序環流控制器的使用增加了控制系統的復雜性。由于上述方案均存在自身問題，采用耦合電抗器的并聯方案逐漸得到了人們的關注。首先，耦合電抗器只對并聯變換器分支電流的差模分量具有阻尼作用，對其共模分量并無阻尼作用，因此它具有自主均流作用［15］，從而使各并聯變換器電流應力趨于一致，為提升變換器的功率等級打下基礎。同時，在理想情況下兩并聯逆變器分支電流相等，對于異側并聯的耦合電抗器而言不產生磁通，因此與傳統電抗器相比，耦合電抗器的體積可大大減小［16］。此外，耦合電抗器可以實現對零序環流的抑制，文獻［16］和［17］分別分析了移相角對并聯型脈寬調制(pulse width modulation，PWM)整流器交流側和直流側無源元件的影響，并指出通過耦合電抗器可減小零序環流，但并未分析耦合電抗器抑制零序環流的根本原理。

針對上述問題，本文提出了一種由耦合電抗器組成的新型并聯型三相并網逆變器，得出了它的去耦等效電路，并分別在三相靜止坐標系和同步旋轉坐標系下建立了平均模型，闡明了耦合電抗器抑制零序環流的根本機理，解決了零序環流引起的不均流、波形畸變等問題，提高了系統的可靠性和效率。最后，對一組1.5 MW三相并網逆變器進行了仿真驗證，結果證明了上述分析及控制策略的正確性。

1 系統結構

本文所采用的系統結構如圖1所示。前級輸送的電能經直流母線電容C濾波、儲能和穩壓后，送入后級并聯型三相并網逆變器。橋臂A1、B1、C1組成并網逆變器1，橋臂A2、B2、C2組成并網逆變器2，并網逆變器1、2相互并聯，它們的交流輸出分別經電感Lk1和Lk2(k=a，b，c)后連接到一起，進而接入電網。電感Lk1和Lk2之間存在耦合，互感為Mk(k=a，b，c)，且為異側并聯電路;Rak、Rbk、Rck(k=1，2)分別為并網逆變器1、2包含電感電阻在內的每相線路電阻;Udc為直流母線電壓。

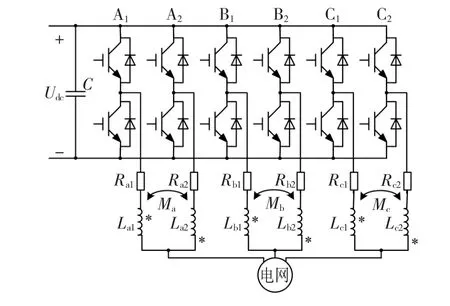
圖1 系統拓撲結構Fig.1 Topology structure of the system

2 模型分析

2.1 去耦等效電路

為了對并聯型三相并網逆變器進行分析，需要對耦合電抗器去耦，從而得到并網逆變器的去耦等效電路，如圖 2 所示，圖中 L′ak=Lak+Ma、L′bk=Lbk+Mb、L′ck=Lck+Mc(k=1，2)，且通常取 Lak=Lbk=Lck=Lk，Rak=Rbk=Rck=Rk(k=1，2)，Ma=Mb=Mc=M;il為前級所傳送的直流電流;iak、ibk、ick(k=1，2)分別為并網逆變器1、2的三相并網分支電流;ea、eb、ec分別為電網三相電壓。

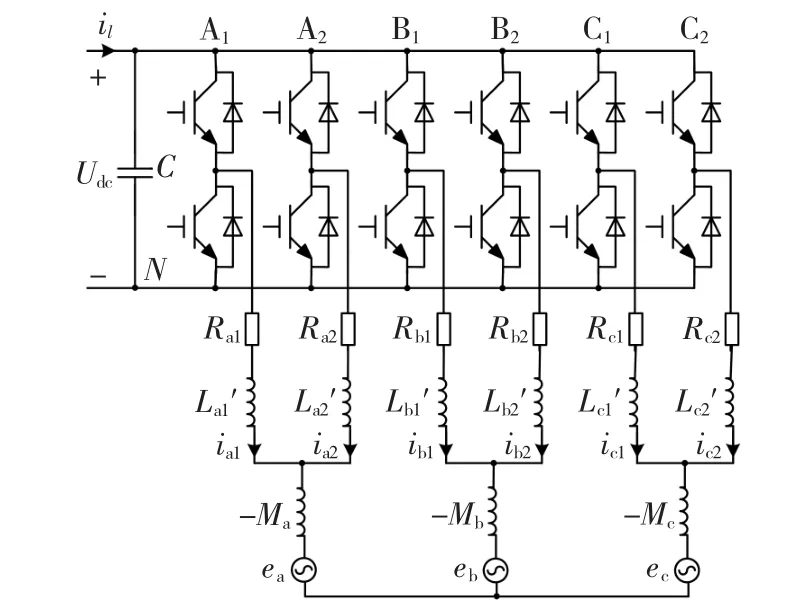
圖2 去耦等效電路Fig.2 Decoupling equivalent circuit

2.2 三相靜止坐標系下平均模型

根據每相橋臂的平均模型［14］，由基爾霍夫電壓、電流定律可以得到由占空比表示的并聯型三相并網逆變器的數學模型:

式中:L′k=L′ak=L′bk=L′ck(k=1，2);dak、dbk、dck(k=1，2)分別為并網逆變器1、2的三相橋臂占空比;UNO為負直流母線N與電網電壓中性點O之間的電壓;ia、ib、ic為三相總電流，即

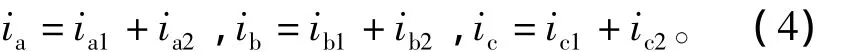
2.3 同步旋轉坐標系下平均模型

在設計控制系統時，通常需要進行坐標變換，將三相靜止坐標系下的時變交流量轉換為同步旋轉坐標系下的直流量，從而簡化控制器的設計。根據等幅值原則，坐標變換矩陣為［14］

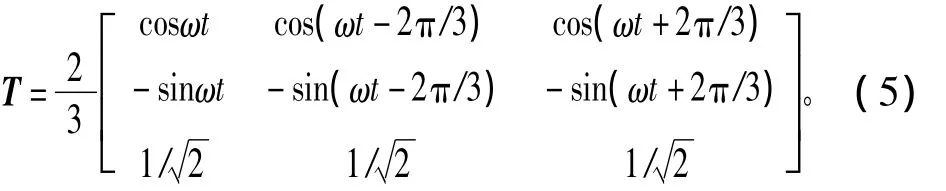
式中:ω為電網同步角速度。三相靜止坐標系下物理量和同步旋轉坐標系下物理量的關系可表示為

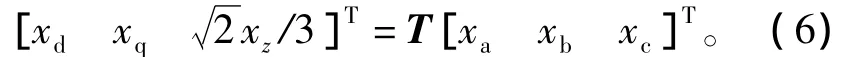
根據式(1)～式(3)描述的三相靜止坐標系下并聯型三相并網逆變器的平均模型，可以得到同步旋轉坐標系下的平均模型，即

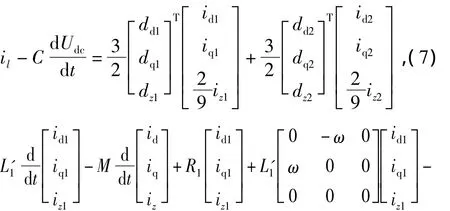
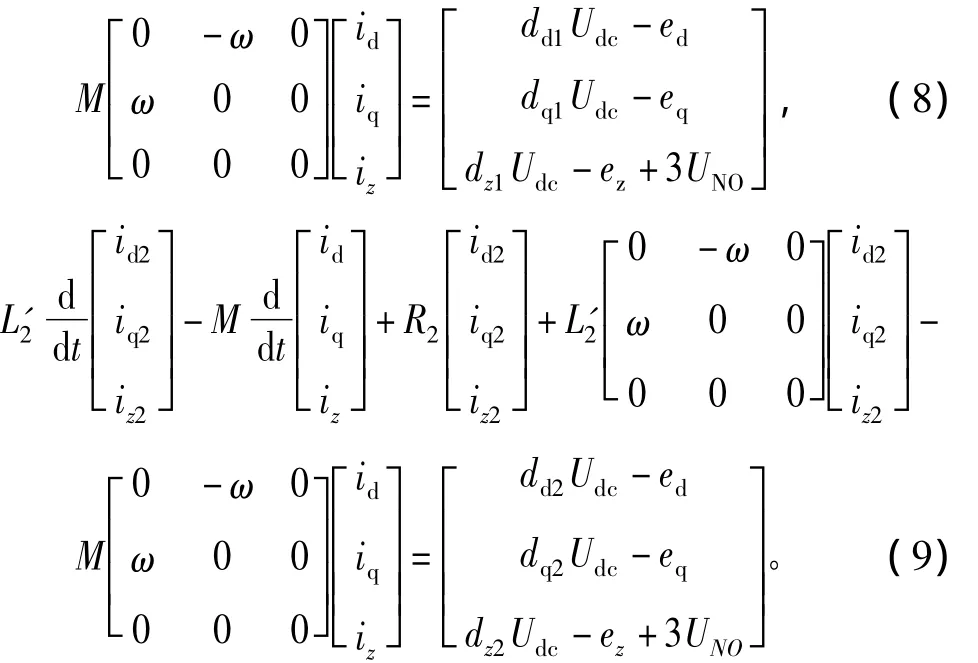
式中:

由式(7)～式(10)可以得到并聯型三相并網逆變器的等效電路，如圖3所示。可以看出，d軸電流分量id1、id2通過電感－M及受控電壓源(－ωMiq)耦合到一起，這增加了控制的難度。由于d軸、q軸具有對稱性，因此對于q軸電流分量可以得出似結論。從圖中z軸等效電路可以看出，零序環流阻抗為(L1+L2+R1+R2+2M)，而采用普通三相電抗器時零序環流阻抗僅為(L1+L2+R1+R2)［14］，因此采用耦合電抗器時零序環流阻抗較大，起到了抑制零序環流的作用，尤其對高頻零序環流效果更為明顯。它的使用省去了交流側笨重的隔離變壓器及復雜的零序環流控制器，降低了生產成本，減小了并網逆變器的體積、重量，并簡化了控制系統的設計，提升了并網逆變器的性能。

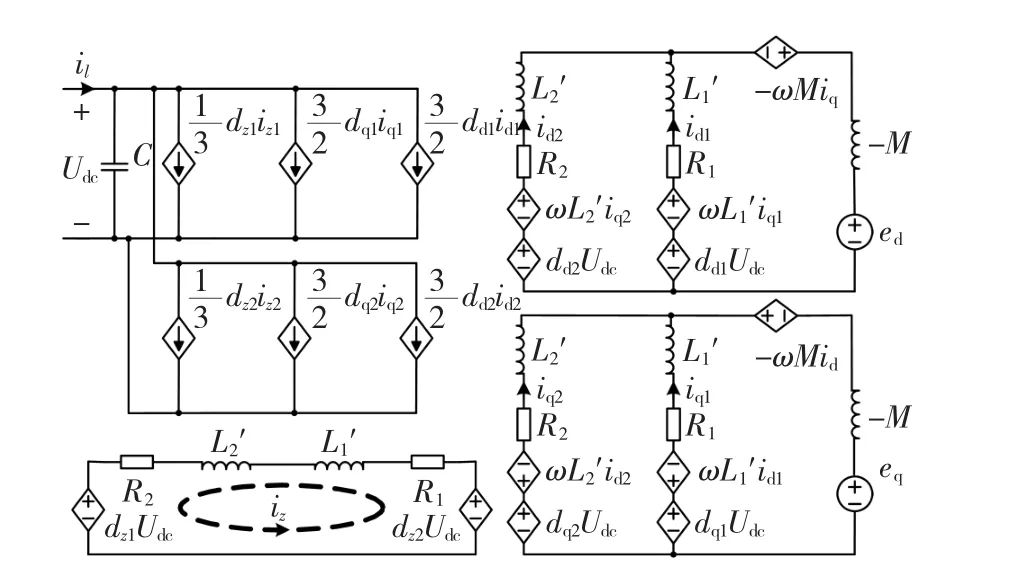
圖3 同步旋轉坐標系下等效電路Fig.3 Equivalent circuit in the synchronous rotating coordinates

定義izs為并聯型三相并網逆變器的系統零序環流，且

則零序環流可以進一步分別表示為

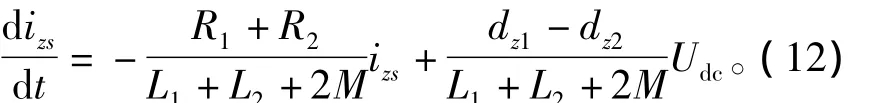
3 系統控制策略

根據同步旋轉坐標系下并聯型三相并網逆變器的平均模型，設計了控制策略，如圖4所示。

圖4 系統控制策略Fig.4 Control strategy of the system

并網逆變器1、2使用共同的電壓外環、獨立的電流內環。電壓環的作用主要是維持直流母線電壓的穩定，從而使能量從直流側輸送到電網，它的輸出經電流權重分配后，分別作為并網逆變器1、2的d軸電流給定id1ref、id2ref。在逆變器容量一定的情況下，為最大地將能量輸送到電網，兩逆變器q軸電流給定iq1ref、iq2ref一般設為零，從而實現單位功率因數并網。

由于通常并網逆變器1、2之間存在對稱性，且電流環d軸、q軸分量之間也存在對稱性，因此并網逆變器1、2的d軸、q軸電流環控制器可使用相同的控制參數。由于耦合電抗器的使用，使得并網逆變器1、2之間互相耦合，且對每個并網逆變器來說，d軸、q軸分量之間也存在相互耦合，為消除這些影響，在設計電流環時需采用前饋解耦控制策略。以并網逆變器1的d軸電流環控制器為例，將解耦項(ωL′1iq1－ωMiq)補償到PI調節器的輸出，即可以起到并網逆變器1、2之間解耦的作用，又可以使電流環d軸、q軸分量之間實現解耦。此外，電網電壓d軸前饋分量ed抵消了實際中電網電壓的影響，進而得到并網逆變器1的d軸輸出參考電壓ud1。得到d軸、q軸輸出參考電壓后，經坐標反變換送入SVPWM模塊，進而得到三相占空比信號，從而實現對并網逆變器的控制。

4 仿真分析

為了驗證上述模型及控制策略的正確性，本文對一組1.5 MW并聯型三相并網逆變器進行了仿真驗證，并將采用普通電抗器與采用耦合電抗器兩種情況進行了對比，以更好地突出耦合電抗器在并聯型三相并網逆變器中的作用。仿真采用690 V電網系統，即ea=eb=ec=690 V;由于1.5 MW并網逆變器多采用1 700 V電壓等級IGBT，考慮到IGBT耐壓能力，同時防止出現過調制，調制方式采用 SVPWM，直流母線電壓取為1 100 V，即Udc=1100 V;直流母線電容 C=6 800 μF;L1=L2=200 μH;考慮到零序環流抑制以及兩并網逆變器的控制效果，取耦合系數k為0.415，則互感

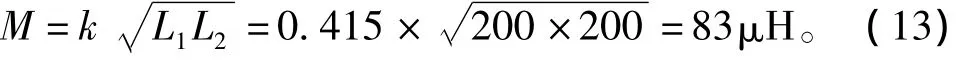
圖5為兩并網逆變器的零序環流仿真波形。從圖5(a)可以看出，采用普通電抗器時零序環流嚴重，峰值幾乎達到了500 A。從圖5(b)可以看出，采用耦合電抗器時零序環流大大減小。零序環流的大小受兩并網逆變器之間參數一致性的影響，如電感值、IGBT開關特性等參數的影響，通過改善參數一致性可進一步減小零序環流。從圖中還可以看出，兩零序環流iz1、iz2大小相等、方向相反。

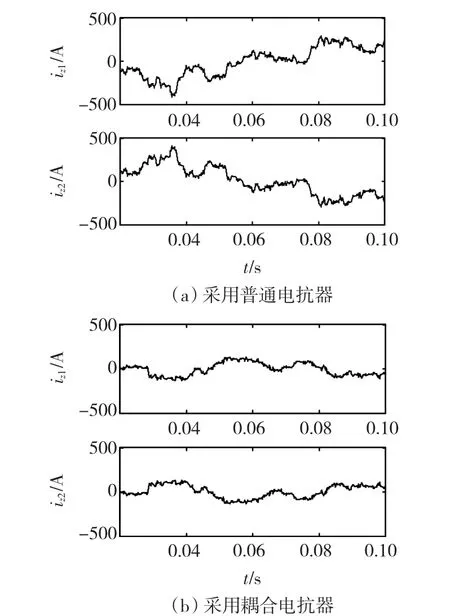
圖5 兩并網逆變器的零序環流波形Fig.5 Zero-sequence circulating currents of two grid-connected inverters

圖6為兩并網逆變器的a相分支電流波形。從圖6(a)可以看出，采用普通電抗器時兩分支電流存在波形不一致、畸變等問題。從圖6(b)可以看出，采用耦合電抗器時兩分支電流一致性良好，且波形正弦。但是由于耦合電抗器的使用，使得兩并聯逆變器之間存在耦合，這在一定程度上會對電流總諧波畸變率(total harmonic distortion，THD)產生負面影響，但總體而言，由于耦合電抗器降低了波形畸變等問題，電流THD還是降低了，從而降低了系統對電網的諧波污染。

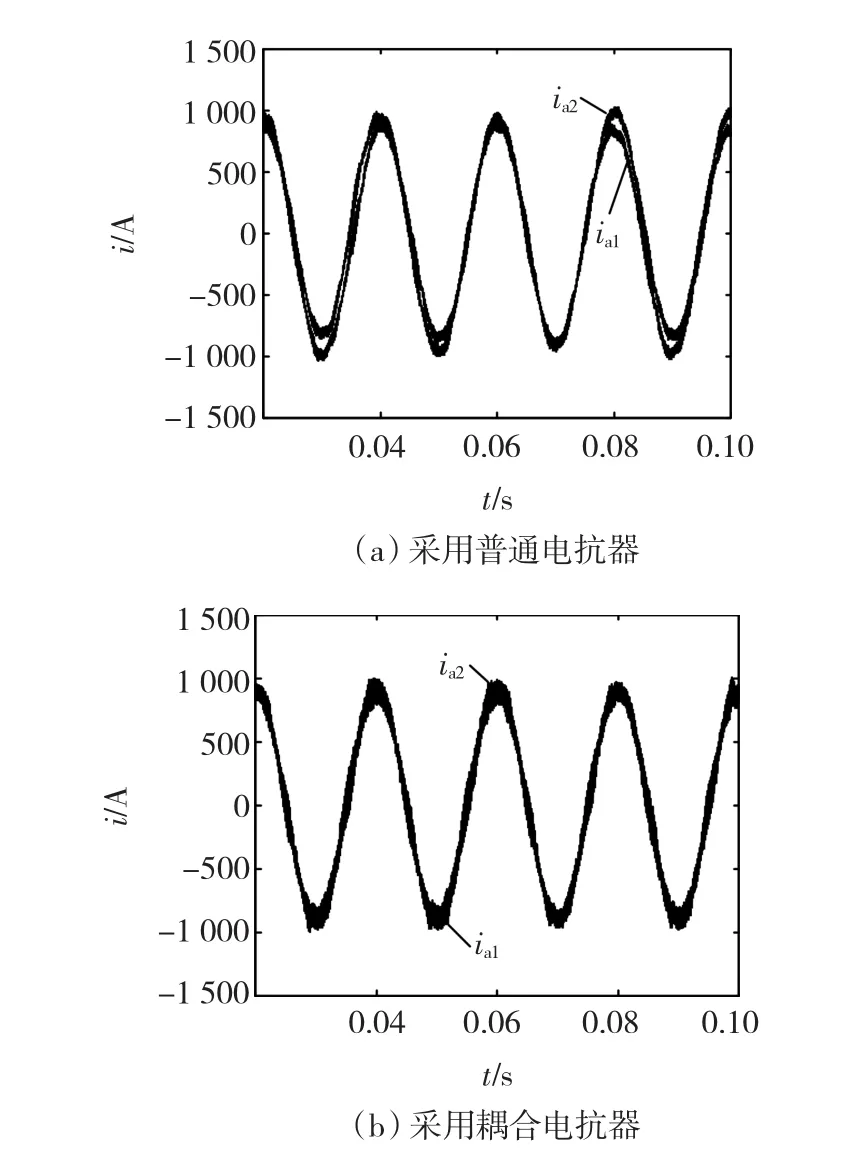
圖6 兩并網逆變器的a相分支電流波形Fig.6 Phase a branch currents of two grid-connected inverters

圖7為并網逆變器1的三相分支電流仿真波形。從圖7(a)可以看出，采用普通電抗器時三相電流存在畸變、不對稱等問題。從圖7(b)可以看出，耦合電抗器的使用減輕了三相電流畸變、不對稱等問題。

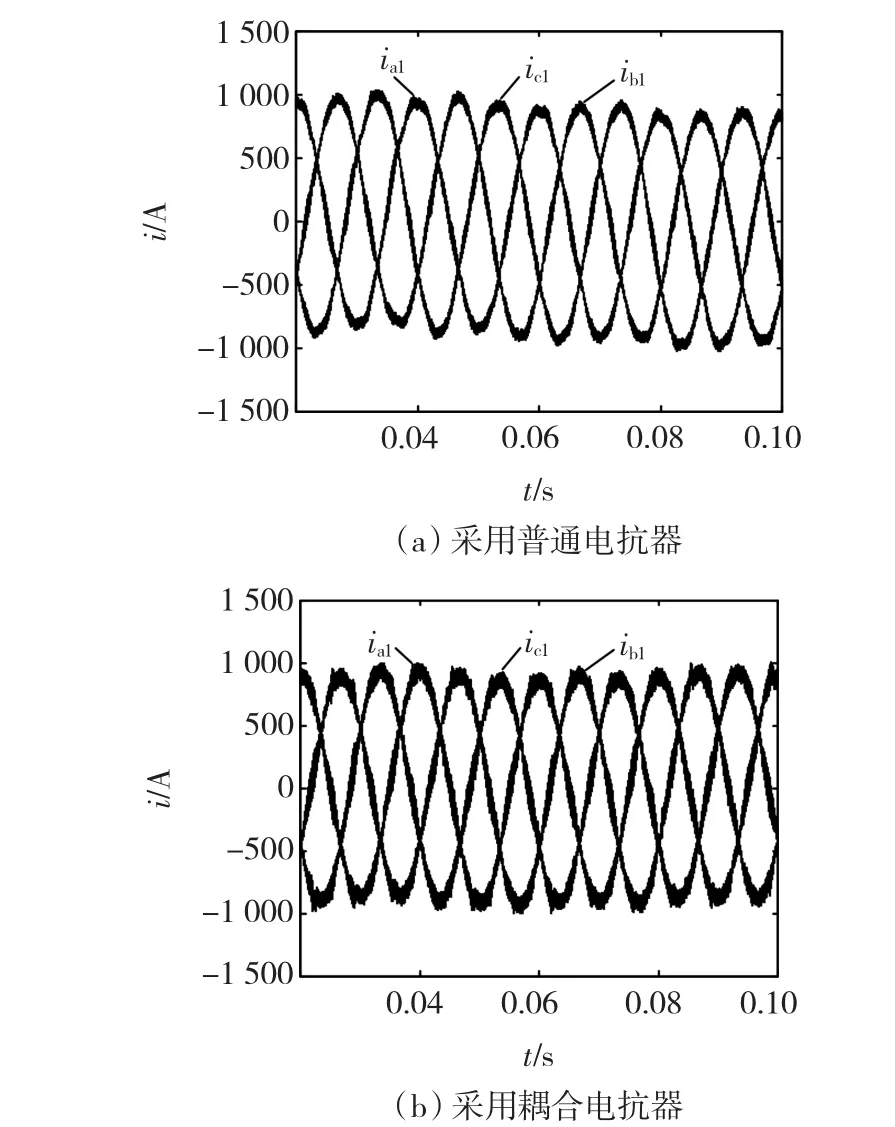
圖7 并網逆變器1的三相分支電流波形Fig.7 Three-phase branch currents of grid-connected inverter 1

圖8為采用耦合電抗器時并聯型并網逆變器的三相總電流波形及電網電壓、電流相位關系，從圖8(a)可以看出，總電流波形三相對稱、正弦性良好。圖8(b)為采用耦合電抗器時電網電壓、電流相位關系，可以看出，電網電壓與電流相位相差180°，系統工作在單位功率因數逆變狀態。

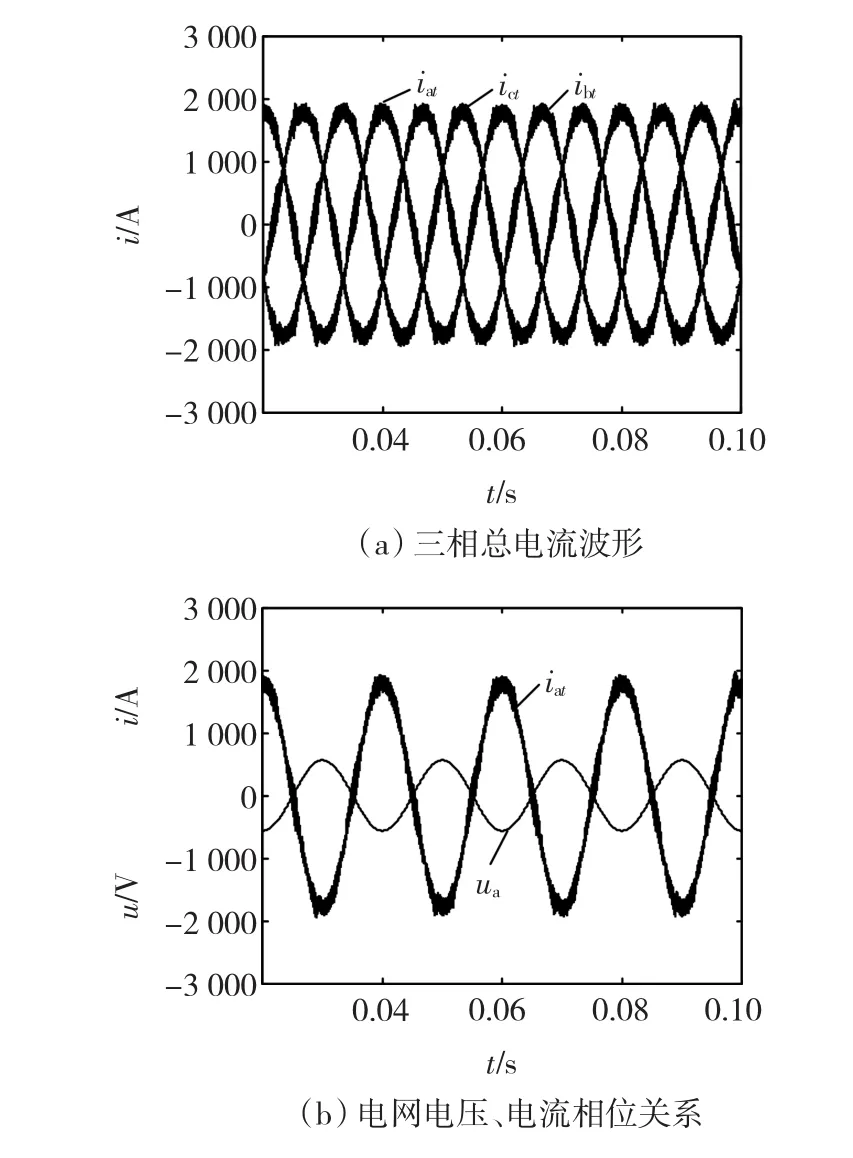
圖8 采用耦合電抗器時三相總電流波形及電網電壓、電流相位關系Fig.8 Three-phase total currents and phase-relationship between grid voltage and current using interphase inductors

5 結論

本文通過對由耦合電抗器組成的新型并聯型三相并網逆變器的研究，得出了它的去耦等效電路及平均模型，闡明了耦合電抗器抑制零序環流的根本機理，即采用耦合電抗器時并聯型三相并網逆變器的零序環流阻抗大于采用普通三相電抗器時的零序環流阻抗，因此耦合電抗器的使用可以對零序環流起到抑制作用，解決了零序環流引起的不均流、波形畸變等問題，提高了系統的可靠性和效率，從而為生產更高功率等級的并網逆變器產品奠定了基礎。

［1］ GABE I J，MONTAGNER V F，PINHEIRO H.Design and implementation of a robust current controller for VSI connected to thegrid through an LCL filter［J］.IEEE Transactions on Power Electronics，2009，24(6):1444－1452.

［2］ 王繼東，朱雪玲，蘇海濱，等.三相光伏并網Z－源逆變器的比例諧振控制［J］.電機與控制學報，2010，14(4):86－91.

WANG Jidong，ZHU Xueling，SU Haibin，et al.Proportional-resonant control for Z-source inverter in three-phase PV grid-connected system［J］.Electric Machines and Control，2010，14(4):86－91.

［3］ SERPA L A，PONNALURI S，BARBOSA P M，etc.A modified direct power control strategy allowing the connection of three-phase inverters to the grid through LCL filters［J］.IEEE Transactions on Industry Applications，2007，43(5):1388 －1400.

［4］ 胡雪峰，龔春英，陳新.采用垂直多載波調制技術的并網逆變器［J］.電機與控制學報，2011，15(7):60－64，70.

HU Xuefeng，GONG Chunying，CHEN Xin.A grid-connected inverter based on vertical layered multi-carrier modulation strategy［J］.Electric Machines and Control，2011，15(7):60 －64，70.

［5］ LOH P C，HOLMES D G.Analysis of multiloop control strategies for LC/CL/LCL-filtered voltage-source and current-source inverters［J］.IEEE Transactions on Industry Applications，2005，41(2):644－654.

［6］ 鄧翔，胡雪峰，龔春英.LCL濾波并網逆變電源的控制策略研究［J］.電機與控制學報，2011，15(5):37－41.

DENG Xiang，HU Xuefeng，GONG Chunying.Study on control scheme for grid-connected inverter with LCL filter［J］.Electric Machines and Control，2011，15(5):37 －41.

［7］ PRODANOVIC M，GREEN C T.Control and filter design of three-phase inverters for high power quality grid connection［J］.IEEE Transactions on Power Electronics，2003，18(1):373－380.

［8］ 汪洪亮，岳秀梅，裴雪軍，等.逆變器并聯系統的新功率算法及實現［J］.電機與控制學報，2010，14(5):37－43.

WANG Hongliang，YUE Xiumei，PEI Xuejun.New power calculation method and realization of parallel inverters［J］.Electric Machines and Control，2010，14(5):37 －43.

［9］ 于瑋，徐德鴻.基于虛擬阻抗的不間斷電源并聯系統均流控制［J］.中國電機工程學報，2009，29(24):32－39.

YU Wei，XU Dehong.Control scheme of parallel UPS system based on output virtual resistance［J］.Proceeding of the CSEE，2009，29(24):32－39.

［10］ 李立，黃松柏，汪洪亮.基于電壓/電流控制模式的組合式三相逆變器［J］.電機與控制學報，2011，15(2):63－70.

LI Li，HUANG Songbai，WANG Hongliang.Combined three －phase inverter operating in voltage or current controlmode ［J］.Electric Machines and Control，2011，15(2):63 －70.

［11］ 毛惠豐，陳增祿.SPWM多重化并聯逆變器的死區效應補償方法的研究［J］.電力電子技術，2004，4(3):49－55.

MAO Huifeng，CHEN Zenglu.Analysis for compensation of dead-time effects for multiple-SPWM inverters in parallel［J］.Power Electronics，2004，4(3):49－55.

［12］ 魏永清，張曉鋒，喬鳴忠.采用參考電壓調節的并聯逆變器控制技術［J］.電機與控制學報，2011，15(2):84－88.

WEI Yongqing，ZHANG Xiaofeng，QIAO Mingzhong.Parallel control technique ofmultiple inverters based reference voltage regulation［J］.Electric Machines and Control，2011，15(2):84－88.

［13］ Dixon J W，Ooi B T.Series and parallel operation of hysteresis current-controlled PWM rectifiers［J］.IEEE Transaction on Industry Applications，1989，25(4):644 －651.

［14］ 李瑞，徐壯，徐殿國.并聯型永磁直驅風電系統的環流分析及其控制［J］.中國電機工程學報，2011，31(6):38－45.

LI Rui，XU Zhuang，XU Dianguo.Analysis and control of circulating current in parallel permanent-magnet-direct-drive wind power system［J］.Proceeding of the CSEE，2011，31(6):38 －45.

［15］ INGYU Park，SEONIK Kim.Modeling and analysis of multi-interphase transformers for connecting plural power converters in parallel［C］.Power Electronics Specialists Conference.St.Louis，USA，1997:1164－1170.

［16］ DI Zhang，FRED Wang，ROLANDO Burgos，et al.Impact of interleaving on AC passive components of paralleled three-phase voltage-source converters［J］.IEEE Transactions on Industry Applications，2010，46(3):1042－1054.

［17］ DI Zhang，FRED Wang，ROLANDO Burgos，et al.DC-link ripple current reduction for paralleled three-phase voltage-source converters with interleaving［J］.IEEE Transactions on Power E-lectronics，2011，26(6):1741 －1753.