LFMCW 激光雷達門限檢測技術

張曉永，王 勇，陳 峰

(駐焦作地區軍事代表室，焦作 454001)

1 中頻信號的噪聲頻域統計特性

經長時間的大量觀察，LFMCW 雷達混頻器輸出的噪聲是窄帶的零均值高斯噪聲(圖1 為中頻噪聲的采樣樣本)，其概率密度由式(1)給出［1］。

此處，p(ε)dε 是噪聲電壓處于ε 和ε +dε 之間的概率;σ2是噪聲方差，噪聲的均值為零。對于連續波雷達回波而言，由于采取了去調頻(兩路具有相同調頻斜率與掃頻帶寬的信號進行混頻輸出)的處理方式，目標的信息完全包含于其回波的頻率之中，因此，探測門限須在頻域進行設置。

由圖1 可以看出，中頻噪聲基本服從均值為零的正態分布，為分析方便，本文采用正態分布模型來描述中頻噪聲。由于噪聲在頻域中分布也具有隨機性，即在頻域中，噪聲中的某一頻率的幅度不是恒定不變的，是具有隨機性的。這一點可以由以下分析得出。

不失一般性，設中頻輸出的噪聲為平穩高斯過程［2］(樣本函數的統計平均可用其時間平均代替)，在混頻器輸出僅有噪聲存在的情況下，對中頻信號采樣并抽取長度為N1的序列。對高斯噪聲采樣序列noise(n)進行離散傅立葉變換，變換如下［3］:

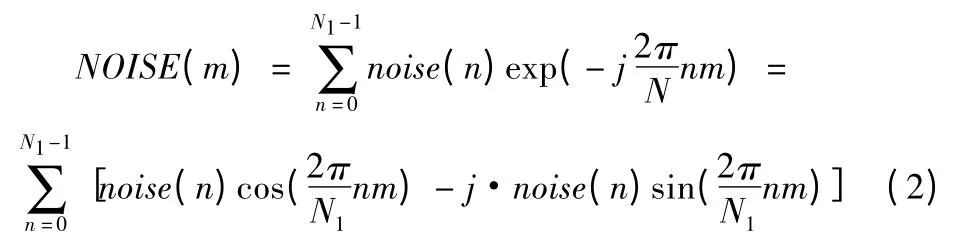
式中m=0，1，…，N1-1。

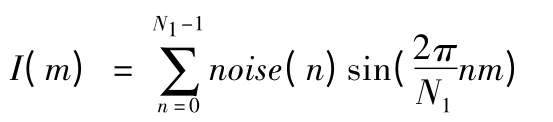
圖1 中頻噪聲的一次采樣時域圖及正態擬合曲線

顯然R(m)，I(m)為高斯序列的線性組合，因此，R(m)，I(m)仍為高斯分布的序列。因高斯分布的概率密度函數由其均值與方差決定。下面求解R(m)，I(m)的均值與方差。

R(m)與I(m)的協方差為:

對于兩個高斯分布，其相關系數為0 與這兩個高斯分布相互獨立是等價的［4］。由此可得出結論①:R(m)與I(m)為兩個相互獨立并服從同一高斯分布。即NOISE(m)(m =0，1，…，N1-1)的實部 R (m)與虛部 I (m)獨立并服從同一高斯分布

在頻域中對信號進行檢測，要對中頻采樣序列的DFT 結果取模，然后進行過門限檢測。因此，有必要求解(或的分布(或等價分布)。

至此，中頻信號中的噪聲頻域統計特性數學模型建立完畢。對于門限檢測，兩個比較重要的指標是虛警概率與探測概率。對于本系統，其虛警概率主要由噪聲的頻域統計特性以及探測門限決定，下面將推導頻域探測門限與虛警概率之間的關系。

2 探測門限與虛警概率的關系

虛警概率Pfa是指在沒有信號僅有噪聲時，發生因噪聲引起電平超過探測門限值被誤認為信號的事件的概率。顯然，它與噪聲的頻域統計特性、噪聲功率以及門限電平的大小密切相關。下面定量地分析它們之間的關系。在推導探測門限與虛警概率關系之前，先介紹一下正確不發現概率:不存在目標判為無目標，稱之為正確不發現，它的概率稱為正確不發現概率Pan。

設頻域探測門限為Q，由于實際處理過程中，會將信號的離散傅立葉變換結果取模，由結論②可知，對于特定的k0，正確不發現的概率Pan(m0)可由χ2(2)分布求得，即:Pan(m0)=P(0≤

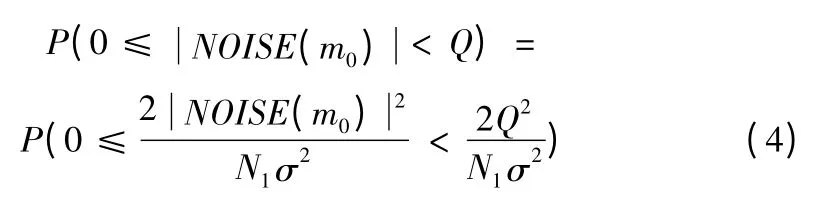
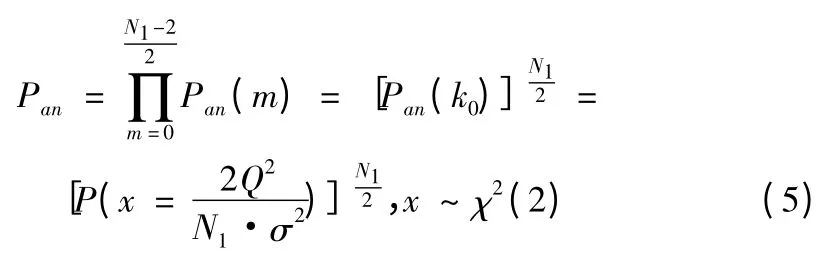
因此，總的虛警概率為

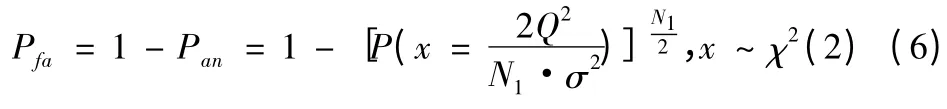
如圖2 所示為N1=1 024 時，虛警概率隨探測門限的變化曲線。可以看到，隨著探測門限的提高，虛警概率不斷的減小，當探測門限Q ＞40σ 時，Pfa迅速下降，這種性質是由χ2(2)分布決定的。

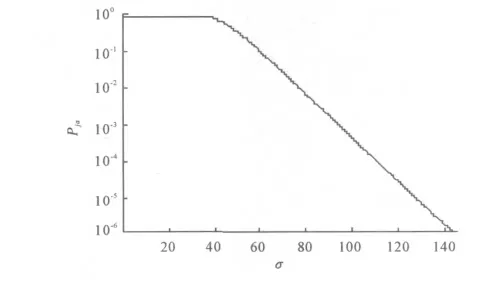
圖2 虛警概率隨探測門限的變化曲線

另外不難看出，當探測門限與噪聲功率一定情況下，虛警概率隨N1的增加而增大，這是因為N1的增加，帶來了更多可引起虛警的“機會”。

3 探測門限與發現概率pd 的關系

探測概率(發現概率)是指目標存在時，判斷為有目標的概率。對于調頻連續波激光雷達探測單目標時，可以抽象為單頻正弦信號加高斯噪聲的中頻信號的發現概率pd。

設N1點的中頻信號序列為:

設x(n)，sIF(n)與noise(n)經DFT 后得到的序列分別為X(m)，SIF(m)與NOISE(m);假設某一ms恰使得為小于N1的正整數)。因此，正確發現目標的事件就是超過預設的探測門限Q。由于NOISE(m)經N 點DFT的結果已經分析，現分析SIF(ms)。

令

由1 節關于NOISE(m)的假設可有:

由式(11)并結合結論①可得出結論③:R(mS)+RS(mS)服從服從分布，并且兩者相互獨立。

正確發現目標的概率可表示為如下形式:pd= P(Q ≤

從結論④中可以得出探測概率的表達式為

由統計知識可知，分布函數ncx2cdf(x，δ)具有一條重要的性質:ncx2cdf(x，δ)隨x 的減小或δ 增大而減小。由此可得出以下四點結論:

第一，在噪聲方差、數據長度、探測門限一定的情況下，探測概率隨中頻信號的信噪比的增加而增大，此時的探測概率完全取決于SNR。如圖3 所示為當N1=512，Q =150σ 時，探測概率隨中頻信號的信噪比變化曲線。

圖3 探測概率隨中頻信號SNR 的變化曲線

第二，隨著N1的增大增大，因此，當探測門限與中頻信號的信噪比不變時，探測概率將會隨著N1的增加而增大。

第三，在探測門限不變的情況下，當中頻信號的信噪比較小時，可以通過增加N1的方法以保證雷達的探測概率。

第四，當噪聲方差、中頻信號的信噪比、N1一定時，探測概率隨探測門限的增加而減小。

至此LFMCW 激光雷達門限檢測數學模型已經建立完畢。

4 結束語

文章針對噪聲在時域和頻域中的統計特性，推導了噪聲功率與虛警概率的關系，同時確立了LFMCW 雷達中頻信噪比與探測概率的函數關系，在此基礎上建立了LFMCW 雷達的頻域檢過門限檢測模型，該模型可為LFMCW 雷達產品定型提供理論參考。

［1］丁鷺飛，耿富錄.雷達原理［M］.西安:西安電子科技大學出版社，2006.

［2］劉次華.隨機過程［M］.武漢:華中科技大學出版社，2001.

［3］胡廣書.數字信號處理［M］.北京:清華大學出版社，2007.

［4］盛聚，謝式千，潘承毅.［M］.北京:高等教育出版社，1997.

［5］李立眾.幾個具有非中心參數的統計量的分布［J］.安徽機電學院學報，1999，14(3):54 -58.

［6］陳希孺.數理統計引論［M］.北京:科學出版社，1981.