基于集員濾波的魚雷聲納子帶自適應(yīng)濾波算法

毛瑞石，李 忠，鄧新文

(91388 部隊(duì)91 分隊(duì)，廣東 湛江 524022)

在許多應(yīng)用中，都需要用到高階自適應(yīng)濾波器。仿射投影算法是NLMS 算法的多維推廣，其收斂性能與歸一化IMS算法相比得到了提高，但增加了計(jì)算復(fù)雜度。Gay［1］和Tanaka［2］等提出的快速仿射投影算法大大降低了仿射投影算法的計(jì)算復(fù)雜度，在快速仿射投影算法中，采用滑動(dòng)窗快速橫向?yàn)V波器算法計(jì)算預(yù)濾波向量，避免了矩陣求逆運(yùn)算。快速仿射投影算法的計(jì)算復(fù)雜度雖然降低了，但其內(nèi)嵌的滑動(dòng)窗快速橫向?yàn)V波器算法的實(shí)現(xiàn)相對(duì)復(fù)雜，并且存在數(shù)值穩(wěn)定性問題。仿射投影算法和歸一化LMS 算法的共同點(diǎn)是有限脈沖響應(yīng)濾波器的抽頭權(quán)值在時(shí)域進(jìn)行調(diào)整。考慮到傅里葉變換將時(shí)域映射為頻域，而反變換則將頻域映射為時(shí)域，Walzman 和Schwartz［3］指出在頻域進(jìn)行濾波器參數(shù)自適應(yīng)調(diào)整同樣可降低輸入信號(hào)的相關(guān)性，基于此思想提出了頻域自適應(yīng)濾波算法。在頻域上去相關(guān)的算法包括變換域算法和子帶算法兩大類，其基本思想是將輸入信號(hào)變到變換域或者分成子帶信號(hào)后，通過(guò)調(diào)整每個(gè)頻帶的信號(hào)功率(或者說(shuō)是調(diào)整對(duì)應(yīng)頻帶的步長(zhǎng))的方法達(dá)到白化輸入信號(hào)的目的，從而增大步長(zhǎng)取值范圍。直接變換自適應(yīng)濾波的典型算法有DCT-LMS 算法、DFT-LMS 算法等。解決長(zhǎng)沖激響應(yīng)濾波器問題的另一種方法是子帶自適應(yīng)濾波，它將輸入信號(hào)和期望信號(hào)分別在子帶空間分解，將信號(hào)能量盡量集中在主瓣內(nèi)，通過(guò)精確的子帶功率估計(jì)加快收斂速度。S.Miyagi 等［4］通過(guò)仿真實(shí)驗(yàn)和性能分析證實(shí)了子帶算法相比于常規(guī)濾波算法的收斂速度得到了很大的提高。

1 子帶自適應(yīng)濾波器

為了解決輸入信號(hào)強(qiáng)相關(guān)情況下LMS 算法收斂速度慢的問題，人們提出了采用子帶算法將全頻帶輸入信號(hào)x(k)通過(guò)分析濾波器組，得到的信號(hào)被下采樣以后再由自適應(yīng)濾波器進(jìn)行濾波，每個(gè)自適應(yīng)濾波器的階數(shù)都低于等價(jià)的全頻帶自適應(yīng)濾波器的階數(shù)(采用一個(gè)近似等于抽取速率的因子)。圖1 所示是它的基本過(guò)程，圖中輸入信號(hào)矢量x(k)=［x(k)，x(k-1)，…x(k-N+1)］T經(jīng)過(guò)分析濾波器組分解為B 個(gè)位于不同頻帶上子帶信號(hào)，用xb(k)表示，0≤b ＜B -1，然后在每個(gè)子帶上分別進(jìn)行自適應(yīng)信號(hào)處理，再把處理后的信號(hào)合成為全頻帶信號(hào)進(jìn)行輸出。將輸入信號(hào)分為若干子帶后并在子帶中經(jīng)過(guò)嚴(yán)格抽取后，每個(gè)信號(hào)的頻譜比初始的全頻段信號(hào)更接近于白噪聲，因此可使每個(gè)子帶信號(hào)的特征值擴(kuò)散度相對(duì)于全頻帶信號(hào)的χ(R)大大減小，并且，隨著子帶數(shù)和抽取比的增加，子帶濾波器長(zhǎng)度和子帶信號(hào)自相關(guān)矩陣的特征值擴(kuò)散度都將進(jìn)一步減小，χ(R)的減小，使得因輸入信號(hào)頻譜起伏變化導(dǎo)致的收斂速度慢的問題得到解決，故子帶自適應(yīng)濾波器較好地解決了傳統(tǒng)全頻帶自適應(yīng)濾波器在面對(duì)長(zhǎng)沖激響應(yīng)模型時(shí)所遇到的問題，同時(shí)對(duì)于每個(gè)子帶濾波器來(lái)，對(duì)應(yīng)每個(gè)子帶的自適應(yīng)濾波器階次比全頻帶自適應(yīng)濾波器階次低了很多，使得計(jì)算復(fù)雜度大大降低。此外信號(hào)被劃分為子帶信號(hào)后，可改變子帶信號(hào)抽樣率以降低運(yùn)算復(fù)雜度。降低信號(hào)抽樣率的過(guò)程稱之為抽取;提高信號(hào)抽樣率的變換過(guò)程稱之為內(nèi)插。圖中，↓D 為抽取過(guò)程;↑D 為內(nèi)插過(guò)程;D 為抽取(內(nèi)插)因子。根據(jù)濾波器組對(duì)輸入信號(hào)頻帶的覆蓋方式不同，子帶分解可分為均勻子帶分解和非均勻子帶分解。均勻子帶分解采用均勻分析濾波器組進(jìn)行，即輸入信號(hào)都被分解為若干個(gè)帶寬相等的信號(hào)，由于對(duì)均勻?yàn)V波器組的研究已經(jīng)比較成熟，因此通常都采用均勻子帶分解。本文將以均勻子帶分解為例，對(duì)子帶自適應(yīng)濾波器進(jìn)行研究。

圖1 子帶自適應(yīng)濾波器結(jié)構(gòu)

2 子帶仿射投影算法

在子帶信號(hào)處理中，濾波器組起著非常重要的作用。它由圖中的分析濾波器組Hb(Z)和綜合濾波器組Gb(Z)組成，其中b=0，1…，B-1。在理想情況下，這些濾波器沒有重疊通帶部分，而是共同覆蓋了輸入信號(hào)的整個(gè)頻帶。由于在原始信號(hào)x(k)經(jīng)過(guò)頻帶分解后，每個(gè)分析濾波器的輸出xb(k)具有與原始信號(hào)相同的采樣點(diǎn)數(shù)目，因此所有信號(hào)xb(k)的采樣點(diǎn)總數(shù)是原始信號(hào)的B 倍，當(dāng)采用均勻子帶分解，每個(gè)子帶都有相同的帶寬，由于每個(gè)分析濾波器的輸出帶寬是原始信號(hào)的因此在不破壞原始信息的條件下，我們能夠用小于或等于B 的因子D 對(duì)每個(gè)xb(k)進(jìn)行抽取，如果D ＞B，則由于混疊現(xiàn)象，會(huì)有信息的丟失，將不能恢復(fù)原始信號(hào);當(dāng)D=B 時(shí)，經(jīng)過(guò)抽取后的數(shù)據(jù)量相對(duì)于輸入信號(hào)采樣點(diǎn)保持不變，這種情況稱為臨界(或嚴(yán)格地)抽取分析濾波器組，這時(shí)在輸出端產(chǎn)生了不希望的混疊分量，引起了信號(hào)質(zhì)量的嚴(yán)重下降根據(jù)文獻(xiàn)［3］可得用于回聲消除和系統(tǒng)預(yù)測(cè)多相位自適應(yīng)濾波器結(jié)構(gòu)分別如圖2 和圖3 所示，圖中輸入信號(hào)x(k)和期望信號(hào)d(k)經(jīng)過(guò)正交分析濾波器組(h0，h1，…，hB-1)被分解為B 個(gè)子帶信號(hào)xb(k)、db(k)，0≤i≤B-1，并令Ns×1維向量xbn(k)由xb(k)通過(guò)多相分解得到，其中NS為各子帶濾波器的抽頭權(quán)系數(shù)長(zhǎng)度，b，n =0，1，…，B -1 為子帶多相分解下標(biāo)。

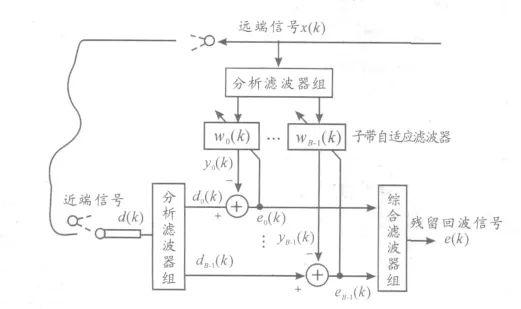
圖2 子帶自適應(yīng)回聲消除系統(tǒng)結(jié)構(gòu)

圖3 子帶自適應(yīng)系統(tǒng)預(yù)測(cè)結(jié)構(gòu)

因用于回聲消除和系統(tǒng)預(yù)測(cè)的原理相同，本節(jié)將以圖3所示的系統(tǒng)預(yù)測(cè)為例研究基于多相分解結(jié)構(gòu)的子帶自適應(yīng)濾波算法，根據(jù)文獻(xiàn)可得基于多相分解結(jié)構(gòu)的子帶仿射投影算法(Sub-APA)權(quán)系數(shù)更新公式:

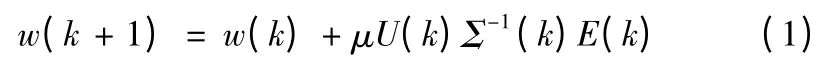
式中:

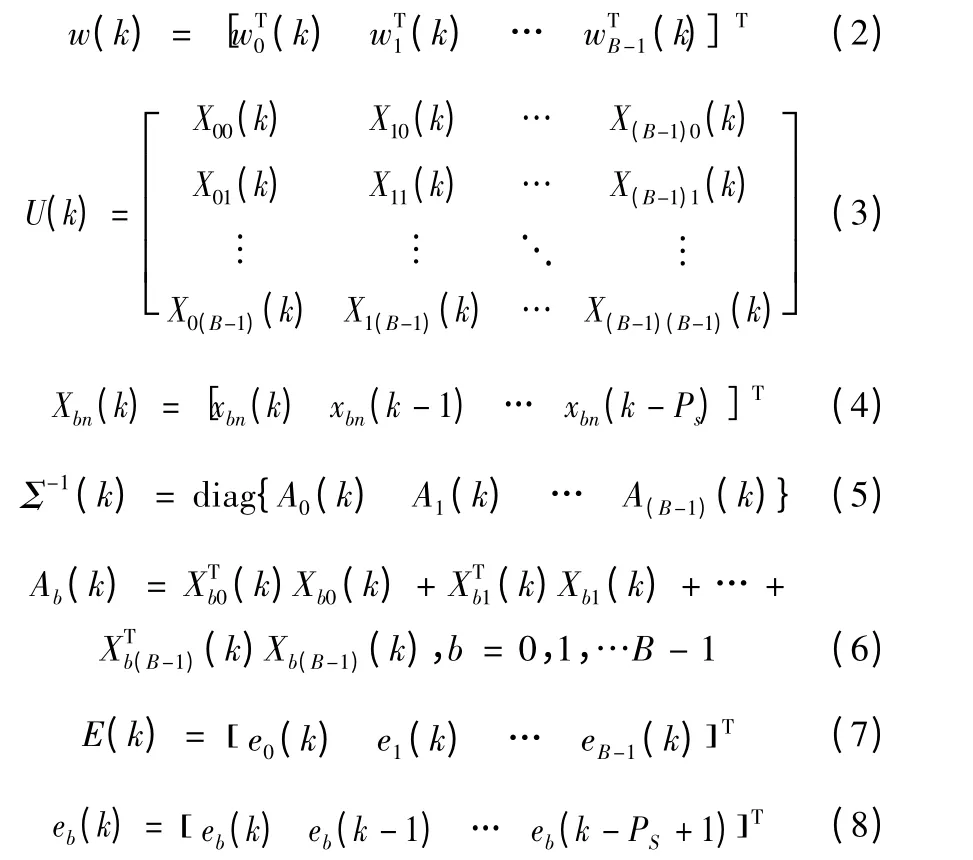
其中:U(k)為BNS×BPS維矩陣;PS為各子帶投影階數(shù);E(k)為BPS×1維向量。

3 基于集員濾波的子帶仿射投影算法

基于多相分解結(jié)構(gòu)的子帶仿射投影算法相對(duì)于文獻(xiàn)［4］中提出的基于此同一濾波器結(jié)構(gòu)的LMS 算法收斂性能得到了改善，但因算法在更新濾波器系數(shù)的過(guò)程中，不僅用到了系統(tǒng)的當(dāng)前信息，而且還需利用系統(tǒng)以前的過(guò)去PS-1 次迭代時(shí)的輸入信號(hào)向量，增加了計(jì)算復(fù)雜度，針對(duì)此問題，可利用集員濾波理論來(lái)減少系數(shù)更新次數(shù)，以保證算法性能的同時(shí)降低其計(jì)算量。

基于多相分解理論，圖3 中自適應(yīng)濾波器系數(shù)可表示為

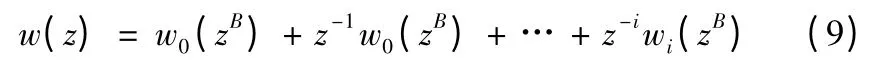
根據(jù)最小擾動(dòng)原理，將基于集員濾波的子帶仿射投影算法(Sm-Sub-APA)設(shè)計(jì)準(zhǔn)則表示為求解如下多約束下最優(yōu)化目標(biāo)函數(shù):

其約束條件為

利用子帶誤差信號(hào)定義和約束條件式(11)得:

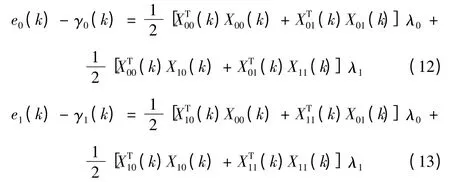
根據(jù)上式，可知λ0、λ1可用式(14)表示:

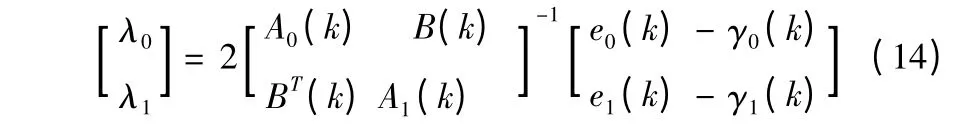
可得B=2 時(shí)子帶分解算法權(quán)系數(shù)更新表達(dá)式:

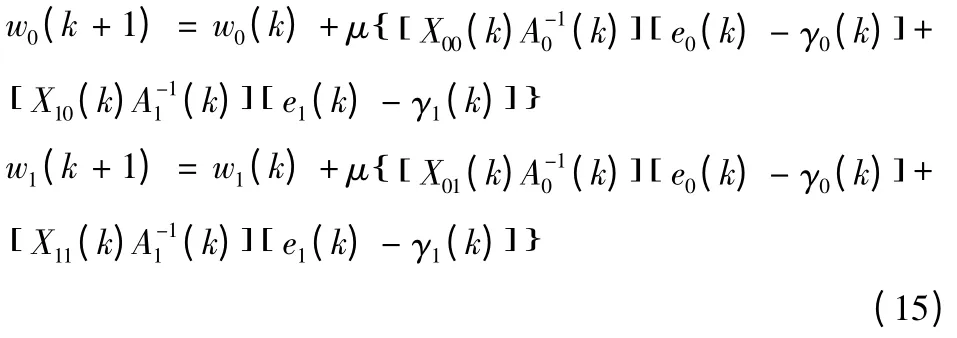
利用式(15)推廣到B(B ＞2)個(gè)子帶的一般情況，可得算法權(quán)系數(shù)遞歸表達(dá)式:

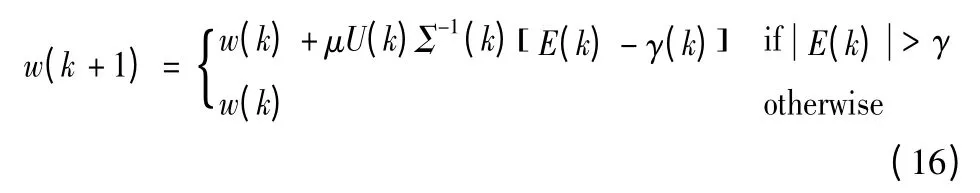
式中:U(k)、Σ-1(k)與子帶仿射投影算法中的相同;Eγ(k)=維 向 量;維向量。

4 仿真結(jié)果

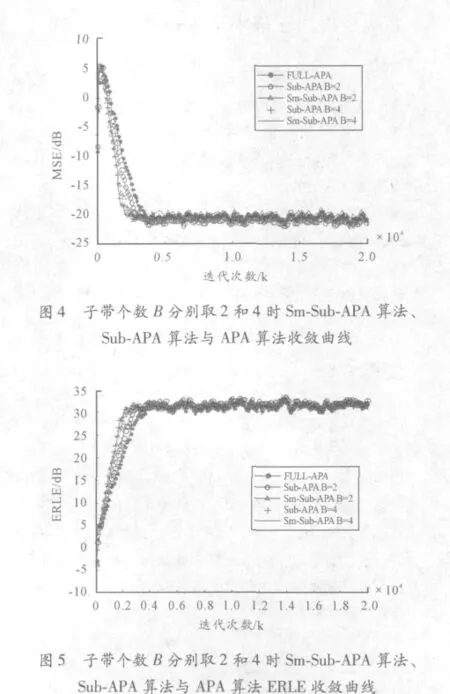
為了檢驗(yàn)上述集員濾波的子帶仿射投影算法的收斂性能，我們以回聲消除問題為例進(jìn)行了計(jì)算機(jī)仿真研究。仿真中回波路徑采用第五章的方法生成，其中ψ 取無(wú)窮;自適應(yīng)濾波器的階數(shù)L=256;仿射投影階數(shù)P，PS均為2，步長(zhǎng)u 均取0.3，子帶個(gè)數(shù)B 分別取2 和4;Sm-Sub-APA 算法中γ 取0.03，期望輸出信號(hào)由輸入信號(hào)與回波路徑卷積后迭加一個(gè)-30 dB 的白高斯觀測(cè)噪聲得到，圖4 和圖5 比較了本文提出的Sm-Sub-APA、子帶仿射投影濾波算法(Sub-APA)以及全頻帶仿射投影濾波算法(full-APA)在以上輸入信號(hào)條件下的均方誤差收斂曲線和回聲衰減增益性能，由圖中可以看出，Sm-Sub-APA 算法、Sub-APA 算法比f(wàn)ull-APA 算法具有更快的收斂速度，Sm-Sub-APA 算法與Sub-APA 算法相比在減少濾波器系數(shù)更新次數(shù)的同時(shí)，保持了同樣高的收斂性能，只是穩(wěn)態(tài)誤差略有增加。從圖中可以看出，當(dāng)子帶個(gè)數(shù)B =2 時(shí)，Sub-APA 算法在經(jīng)過(guò)約3 000次迭代達(dá)到穩(wěn)態(tài)并且回聲衰減增益提高到32 dB 左右，Sm-Sub-APA 算法經(jīng)過(guò)同樣迭代次數(shù)達(dá)到穩(wěn)態(tài)只是回聲衰減增益稍低于32 dB，而full-APA 算法則需要經(jīng)過(guò)約4 000次迭代才能夠進(jìn)入穩(wěn)態(tài)。此外實(shí)驗(yàn)過(guò)程中還發(fā)現(xiàn)，通過(guò)增大子帶個(gè)數(shù)，還可進(jìn)一步加快速度。

5 結(jié)束語(yǔ)

為了改善高階自適應(yīng)濾波器的收斂速度和實(shí)時(shí)實(shí)現(xiàn)性，借鑒了多相分解子帶自適應(yīng)濾波器和仿射投影算法的基本思想，基于輸入信號(hào)為遍歷的寬平穩(wěn)隨機(jī)過(guò)程的假設(shè)，并結(jié)合集員濾波算法的優(yōu)點(diǎn)，提出了一種集員濾波的子帶仿射投影算法，該算法通過(guò)將輸入信號(hào)的子帶分量和濾波器權(quán)矢量分解成多相的形式，消除了傳統(tǒng)臨界采樣濾波器混疊的影響，此外應(yīng)用集員濾波理論克服了仿射投影算法在提高收斂速度的同時(shí)計(jì)算量增加的問題。回聲消除實(shí)驗(yàn)仿真結(jié)果表明:盡管是基于對(duì)輸入信號(hào)的若干假?zèng)]，提出的算法相對(duì)于全帶仿射投影算法收斂速度和回波返回?fù)p失強(qiáng)度得到了明顯改善，且接近子帶仿射投影算法的性能。

［1］Gay S L，Tavathia S. The fast affine projection algorithm［C］.Proc.ICASSP’95，Detroit USA，1995:3023-3026.

［2］Tanaka M，Kaneda Y，Makino S，et al.A fast projection algorithm for adaptive filtering［J］. IEICE Trans. on Fundamentals of electronics，communications and computer sciences.1995，E78-A(10):1355-1361.

［3］Hun Choi，Hyeon-Deok Bae.Subband Affine Projection Algorithm for Acoustic Echo Cancellation System［J］. EURASIP Journal on Advances in Signal Processing，2007:146-157.

［4］Pradhan S S，Reddy V U.A new approach to subband adaptive filtering［J］. IEEE Transactions on Signal Processing，1999，47(3):655-664.

［5］崔旭濤，楊日杰，何友.基于DSP 信號(hào)處理系統(tǒng)的自適應(yīng)濾波器［J］.兵工自動(dòng)化，2010(1):63-65.