導彈控制系統仿真基本方法

楊育榮，王建琦，2

(1.中國空空導彈研究院，河南 洛陽 471009;2.航空制導武器航空科技重點實驗室，河南 洛陽 471009)

數字仿真是將實際系統中的各組成部分全部用數學模型代替，并把數學模型轉換成數字仿真模型，在數字計算機上對實際系統進行仿真研究的過程。它具有如下特點:①經濟性，不需要實物的參與，是最經濟的研究方法;②靈活性，控制系統的研制是不斷完善的過程，如果對產品硬件進行修改，無疑費時費力，而利用數字仿真，通過對數學模型進行修改，可方便地對制導系統的每一部分進行迭代設計和參數優化，更具靈活性，并大大縮短研制周期［1-2］;③通用性，既往型號數學仿真中建立的數學模型經過少許的改進和開發，可以適用于后續型號或派生型號的研究。

本文主要介紹用泰勒級數對導彈控制系統數字仿真的模型化方法，對導彈控制系統數字仿真的方法、步驟、內容以及仿真試驗的設計等進行詳細描述，給出了評價仿真結果的方法。

1 導彈運動方程線性化原理

導彈空間運動通常由一個非線性系數的微分方程組來描述。分析導彈的動態特性，可以采用泰勒級數的線性化方法［3］。假設導彈運動方程為一般形式的微分方程組，即:

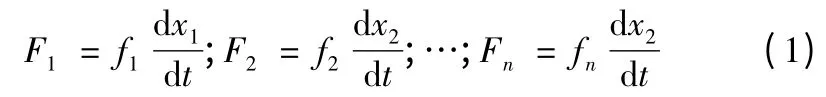
式中:f1，f2，…，fn，F1，F2，…，Fn都是關于導彈運動參數x1，x2，…xn的函數。

由理想彈道計算可得其特解為

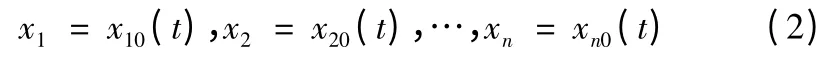
式中下標0 表示基準彈道的參數。將特解式(2)代入式(1)可得

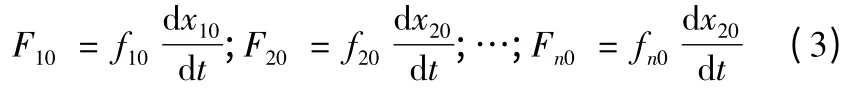
對一般形式的微分方程組(1)進行線性化，為不失代表性，任取一個方程，并省略其下標，有

式中:x 可以代表含擾動作用飛行的任一運動參數，在基準運動中有

一個運動參數在擾動運動和未擾動運動中之差稱為運動參數的偏量(或增量)，其形式為

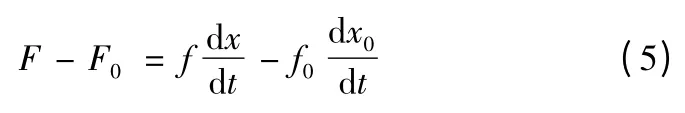
令Δx=x-x0，Δf=f-f0，ΔF=F-F0，因此，式(5)可改寫為

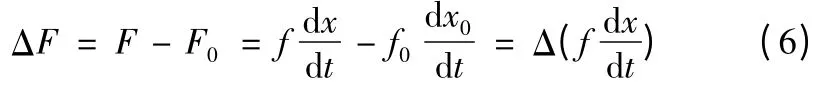
式(6)又可以改寫成

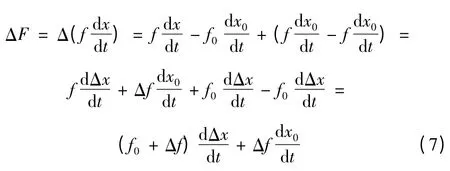
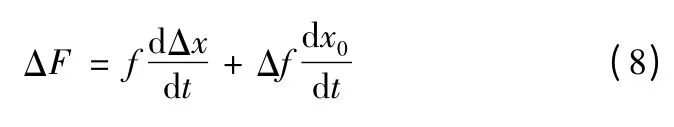
式中:ΔF 和Δf 是函數增量，可由以下方法計算。

將f 在x10，x20，…xn0點附近展開為泰勒級數，且定義f00=f0(x10，x20，…xn0)，則有

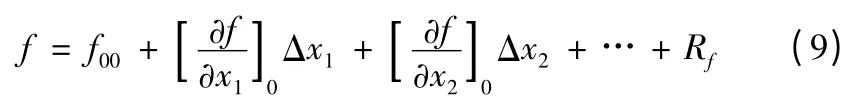
式中Rf是所有高于二階以上各項之和。增量函數Δf 為

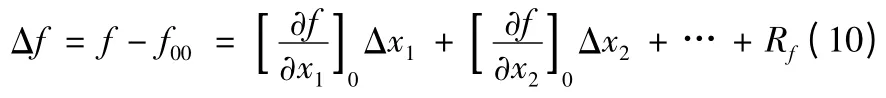
同理可以求得增量函數ΔF 的表達式為

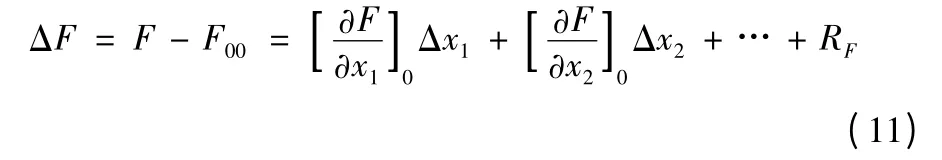
略去高階小量之和，式(8)可以寫為

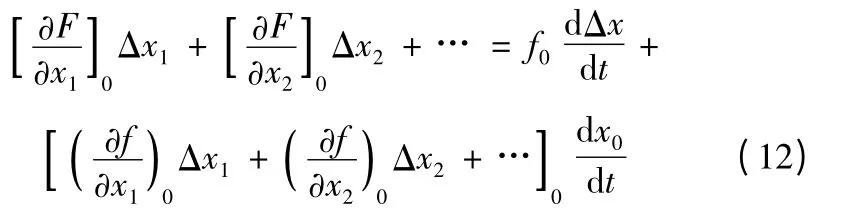
可得任一運動參數的偏量的線性微分方程式

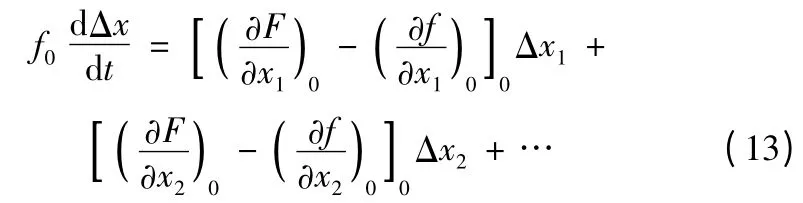
顯然，式(13)中的自變量是運動參數偏量Δx，可以是Δx1，Δx2，…Δxn，偏量在方程式中僅有1 次冪，沒有偏量間的乘積，所以微分方程式(12)是線性的。式中，函數f0以及偏導數等，均是已知的基準彈道運動參數的函數。

2 導彈仿真模型的建立

2.1 彈體縱向運動小擾動模型

利用導彈質心動力學、繞質心轉動動力學、姿態運動學等方程［4］，采用小擾動線性化，忽略二階以上微量以及導彈氣動力、氣動力矩的次要因素時，可使方程實現線性化，得到導彈運動的簡化方程。由導彈彈體縱向運動方程，采用上述線性化方法，可以得到小擾動模型為:

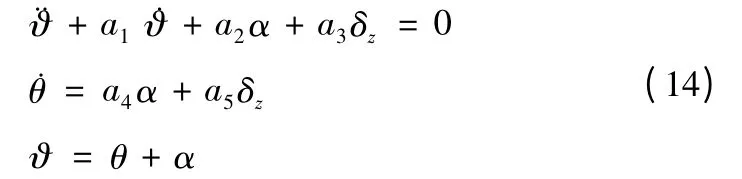
式中:? 為俯仰角;θ 為彈道傾角;α 為攻角;δ 為舵偏角;a1～a5為彈體動力系數，其計算公式為

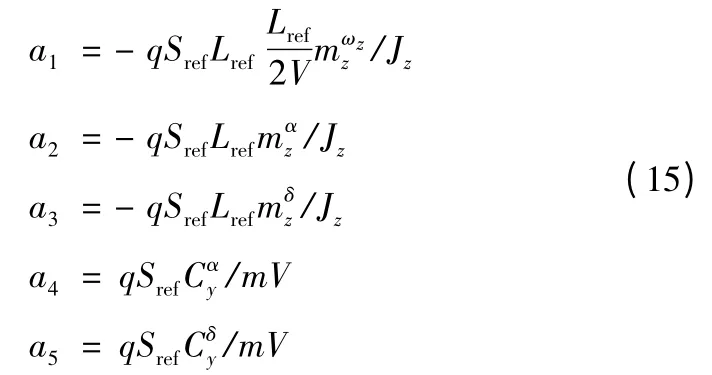
其中:q 為動壓;Sref為參考面積;m 為質量;V 為速度;Lref為參考長度;Jz為轉動慣量為氣動偏導數。

2.2 縱向運動傳遞函數

導彈縱向運動傳遞函數為:

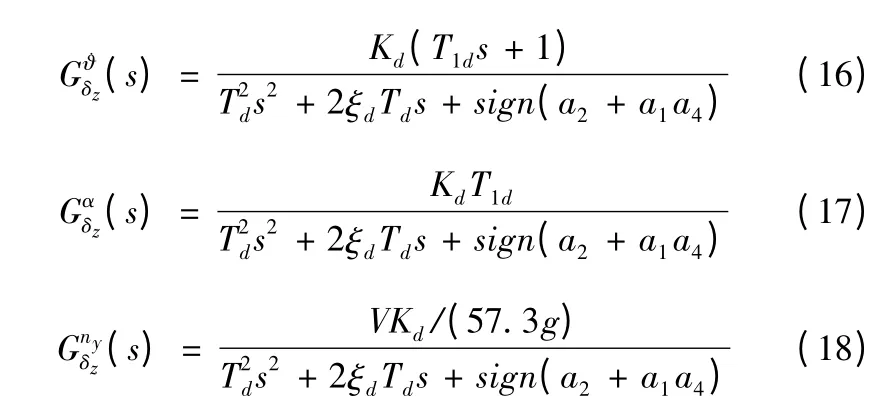
式中傳遞函數系數計算公式為:

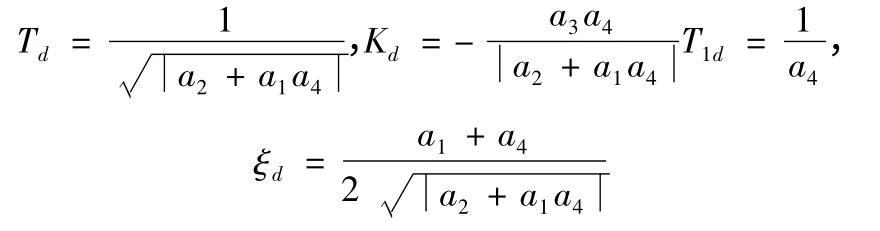
3 導彈控制系統數字仿真

導彈控制系統仿真包括線性化仿真和非線性仿真。線性化仿真是在導彈的飛行空域中，選取特征點，利用固定導彈的飛行高度、馬赫數、攻角、發動機燃燒時間等，利用傳統的控制理論，來研究導彈的閉環時域特性和開環頻域特性［5-6］。

非線性仿真在導彈飛行空域內選取一條特定的彈道進行，其實質為求解高階微分方程，仿真的基本步驟為:

1)寫出實際系統的數學模型;

2)將數學模型二次模型化，轉變成可編程的離散化模型;

3)針對離散化模型，用編程語言編寫仿真程序;

4)仿真結果分析、修改，直至滿足要求。

3.1 線性化仿真

線性化模型是非線性模型的簡化，具有模型簡單、容易實現等特點，一般考慮連續系統，進行時域分析和頻域分析。時域分析對系統施加一定的輸入信號，通過研究系統的時間響應來評價系統性能［7］。對三回路自動駕駛儀來說，時域分析主要對角速度回路、姿態角回路和加速度回路進行閉環分析，考察上升時間(tr)、超調量(σp)、穩態誤差等指標。圖1為某導彈控制系統的階躍響應曲線。

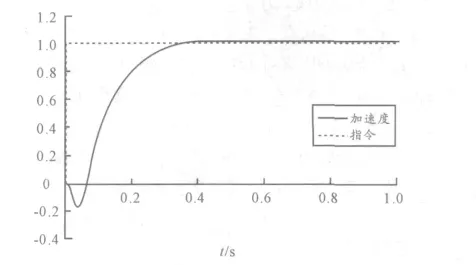
圖1 控制系統階躍響應曲線

導彈控制系統時域指標一般是上升時間小于0.3 s，超調量小于20%，穩態誤差小于10%。從圖1 可以看出，系統階躍響應上升到85%的時間為0.22 s，超調量為1.3%，穩態誤差為0，因此圖1 的系統能夠滿足時域設計要求，但仍需要分析其頻域特性。

頻域分析通過系統開環的頻率特性來進行。開環頻域特性主要分析幅值裕度(Gm)、相位裕度(Pm)等［8］。圖2 所示為圖1 中對應的頻域特性曲線。

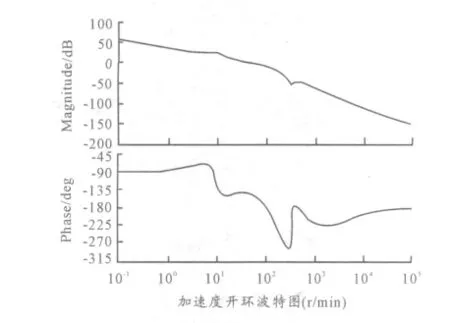
圖2 控制系統頻域特性曲線

導彈控制系統頻域指標一般是幅值裕度大于6 dB，相位裕度大于30 rad/s。從圖2 中可以看出，系統的幅值裕度為7.71 dB，相位裕度為34.1 rad/s。因此，此系統滿足時域、頻域設計要求。

3.2 非線性仿真

現代導彈是一個非常復雜的系統，大攻角、非線性、強耦合等特點決定了導彈控制系統的設計必須要經過嚴格的考核。控制系統在工作過程中，力系數、力矩系數、轉動慣量、推力偏心、推力溫度、舵零位誤差、舵機前向控制增益、初始俯仰角、初始發射速度等都可能影響其性能。這些因素的排列組合將非常龐大，因此需要尋求一種盡量少做仿真試驗但卻能全面考核導彈性能的試驗方法。非線性仿真可以采用單項因素、機彈干擾和正交拉偏等試驗進行［9］。

1)單項因素仿真。只考察某1 個特定參數的影響程度，進行單項因素仿真(包括對這個參數的上拉偏、下拉偏和額定偏仿真)。

2)機彈干擾仿真。在導彈和飛機分離時刻引入1 個初始角速度、攻角、力矩、力等進行發射仿真。

3)正交拉偏仿真。選取n 個不相關的算法影響因素1，2，…，n，每個影響因素有1，2，…，k 個影響水平，需要進行m次試驗才能對算法進行全面仿真。針對這個問題可以構造一個正交表Lm(nk)。表1 所示為正交表L9(34)，其中行表頭表示影響因素，列表頭表示試驗次數，數字1 表示各因素下拉偏仿真，2 表示額定仿真，3 表示上拉偏仿真。

4 仿真實例

圖3 為某次單項因素仿真最大攻角統計曲線。對于圖3中的攻角最大限幅到40°。從圖3 中可以看出，部分仿真結果達到了限幅值，然而氣動數據分析所需要的攻角遠小于仿真值，說明在攻角為40°的仿真系統可能已經發散，需要進一步分析;其他條件仿真結果正常。

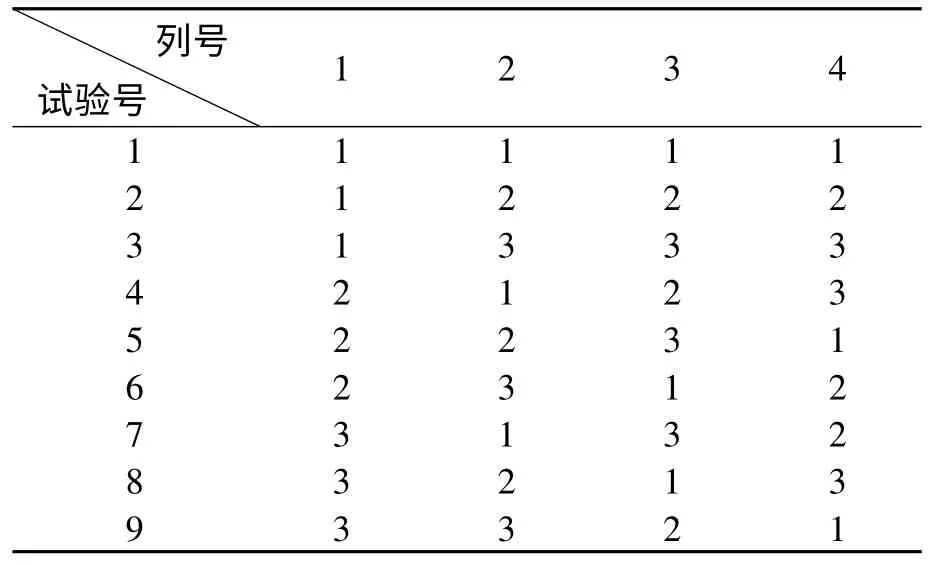
表1 L9(34)正交試驗

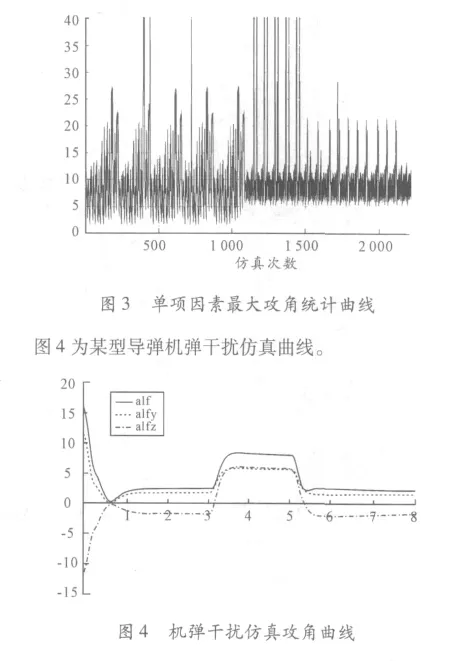
從圖4 中可以看出，初始時刻導彈具有攻角，引入控制后導彈攻角很快穩定，說明若導彈發射攻角小于等于圖4 中的攻角時，系統能夠穩定。

圖5 所示為某次正交拉偏最大通道舵偏統計曲線。

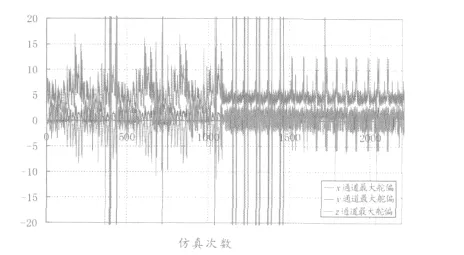
圖5 正交拉偏最大通道舵偏統計曲線

同樣對于圖5 中的最大舵偏也具有限幅值，在達到限幅值的仿真條件中，由于正常仿真情況下，所需要的舵偏小于仿真值，說明在舵偏限幅的仿真條件處系統可能已經發散，這些發散的條件將是控制系統設計迭代時分析的重點彈道。

5 結束語

導彈在論證、方案、工程研制和定型等階段，計算機數字仿真是必不可少的技術手段。數字仿真仿真時間短、可重復，可以用來彌補飛行試驗數據之不足，既可以縮短研制周期，也可以節省大量經費。本文基于傳統的導彈控制系統設計過程，介紹了彈體模型線性化的原理，描述了導彈線性、非線性仿真的基本方法，通過對正交表的描述，介紹了現代導彈控制系統設計過程中所必須的拉偏仿真，并對仿真結果給出了評價的方法。

［1］楊新.飛機六自由度模型及仿真研究［J］.系統仿真學報，2000(5):210-213.

［2］謝曉方，李松陽，孫濤.導彈通用武器控制系統體系結構研究［J］.兵工自動化，2010(1):1-4.

［3］張有濟.戰術導彈飛行力學設計［M］.北京:宇航出版社，1998.

［4］胡小平，吳美平，王海麗.導彈飛行力學基礎［M］.北京:國防科技大學出版社，2006.

［5］劉真，張濤.基于H∞混合靈敏度的導彈穩定控制回路設計［J］.四川兵工學報，2011(7):40-43.

［6］伍曉軍，李翊，孫曉燕，等.基于攻角力測的不確定導彈系統的滑模自適應控制研究［J］.海軍航空工程學院學報，2011(4):410-413.

［7］Bernstein D S.The treatment of inputs in real-time digital simulation［J］.Simulation，1979，33(2):65-68.

［8］Lambert J D.Computational methods in ordinary differential equations［M］.New York:Wiley，1973.

［9］劉瑞葉，任洪林，李志民.計算機仿真技術基礎［M］.北京:電子工業出版社，2004.

［10］許志，林永生，解永鋒，等.基于RTX 的空面導彈制導控制系統快速原型仿真［J］.火力與指揮控制，2010(12):184-187.