基于格型遞歸最小二乘算法的船舶運動極短期預報

彭秀艷，劉長德

（1哈爾濱工業大學航天學院，哈爾濱 150001；2中國船舶科學研究中心，江蘇 無錫 214082）

1 引言

目前，國內外對船舶運動極短期預報都非常重視并展開了許多研究。其中利用時間序列分析法[1]對船舶運動進行極短期預報越來越受到重視，這種方法的最大優點是無需知道海浪的任何先驗信息和船舶航行姿態的狀態方程，僅僅利用歷史數據尋求規律進行預報。這種方法假設船舶在海浪中的運動姿態為一平穩的窄帶隨機過程，從而利用線性模型[2-5]擬合這一過程。

實際應用中，尤其是在極短期預報當中，實時預報[6-7]是我們比較關心的問題。自適應模型在某種程度上能夠實時地根據量測數據和期望輸出自行調整模型參數，并隨著數據的陸續到來，通過遞推算法自動地對模型參數加以修正，使其接近某種最佳值，即便在尚不完全掌握序列特性的情況下也能得到滿意的模型。由于應用遞推算法，自適應模型的參數在每次迭代中要加以修正，因此參數和輸入數據是有關的，這意味自適應模型是非線性的，但習慣上也說是線性自適應模型，這指的是被估計的參數向量是由一組觀察數據的線性組合進行自適應計算得出的[2-4]。

本文在最小二乘方法的基礎上，提出了基于格型實現的RLS算法（LRLS），該算法結構是模塊式的多極格型結構，RLS算法的結構形式是橫向濾波器，因此LRLS算法可以根據需要簡單地增加一級或多級格形結構而不影響原來的計算。LRLS算法的計算量和階數n成線性關系，而RLS算法計算量是隨n2增加的。LRLS降低了一般RLS算法的計算復雜度，收斂速度快，該算法的魯棒性和收斂性都比較好，是一種理想的自適應遞推方法。

2 預報算法

2.1 RLS算法

設t時刻模型的輸入為X（t）=[x（t）,x（ t-1）,…,x（ t-n+1）]T，ε （t）是希望值y（t）與估計值y＾（t）之差，φ（t）= [φ1（t）,φ2（t）,…,φn（t）]T為最小二乘意義下的最優解，則有：

估計誤差為

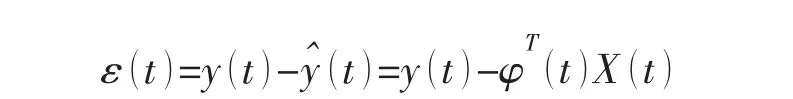
最小二乘的性能指標是使J（t）最小，

式中λ為指數加權因子，由?J/?φ=0可以得出確定最小二乘意義下最優解（t）的正規方程

其中n×n相關陣N（t）和n×1互相關陣M（t）分別為：

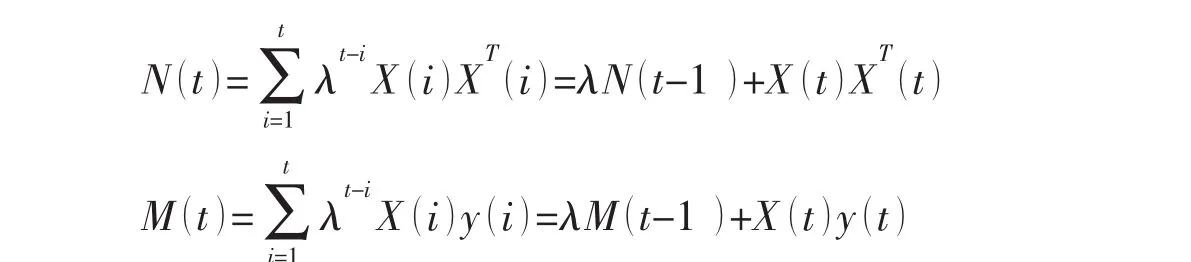
利用矩陣求逆引理[8]可求得（t），且在t=1,2,…過程中是遞推式進行。

初始設定P（0）=δ-1I，（0）=0，I為單位陣（t=1,2,…）。

2.2 前向預報與后向預報

如果預報是根據t-1，…，t-n時刻的數據預報t時刻的值，可稱為前向預報，如果由t，t-1，…，t-n+1時刻的數據預報t-n時刻的值，則稱為后向預報。表1給出了RLS線性估計與前向、后向預報各種變量之間的對應關系。

表1 RLS線性估計與前向、后向預報各種變量對照表Tab.1 The variables about RLS linear estimation,forward prediction and backward prediction

由表1中的對應關系以及RLS算法公式可得前項預報的參數遞推公式。

與前向預報器類似，推導給出反向預報的參數遞推公式如下：

反向（后驗）預報誤差加權平方和最小值的遞推公式為

2.3 LRLS算法

2.3.1 階數更新

令標量

可推得兩個按階數遞推關系式：

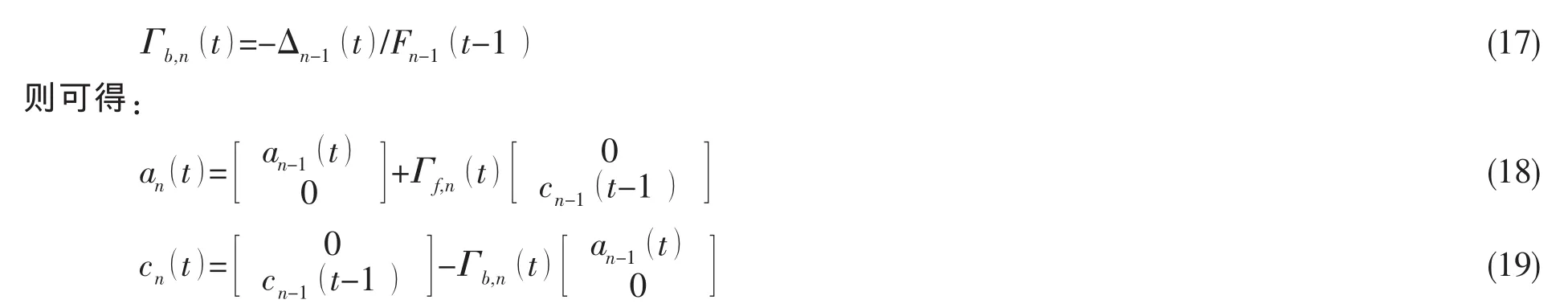
其中：Γf,n（t）和Γb,n（t）分別稱為正向和反向反射系數，進一步可得正向和反向后驗誤差按階數遞推的公式如下：

以上二式可用信號流圖1表示。

圖1 LRLS預報誤差遞推結構Fig.1 Recursive structure of predicted errors about LRLS algorithm

階數n是可變的，它取為0,1,…,N（N是預報階數的終值）。當n=0時沒有對輸入數據作任何預報，這相當于初始值

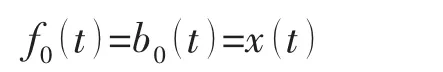
當階數由零變到N可得多級最小二乘格型濾波器如圖1，所含格型結構的級數即為濾波器的階數。

2.3.2 時間遞推

為了使得上述遞推依時間進行自適應遞推，須導出前面計算中所需的Δn-1（t）參數按時間遞推的公式，可推得Δn-1（t）按時間遞推的關系如下

由正向先驗誤差與正向后驗誤差的關系也可將上式寫為

其中，γ（n-1）

t為變換因子，對于正向線性自適應預報有

對于反向線性自適應預報有

3 船舶運動自適應預報模型

3.1 AR預報模型

自回歸（AR）模型。

其中：p 為自回歸階數，φ1，φ2，…，φp為自回歸系數，εt為零均值的正態分布噪聲。

將AR模型變換成（27）式，則AR模型參數可由反射系數求得[9]。

其中l=1,2…為預報步數。應用AIC準則確定階數p[9]，當階數p確定，已知時，便可利用（28）、（29）式和（30）式對船舶運動進行多步預報。

3.2 模型參數遞推估計

由于AR（n）模型類似于n階線性預報器，因此LRLS參數估計公式可應用于AR模型。從t=1開始，按階數n=1,2…,N順序計算（N是最小二乘格形濾波器的最高階數）。

歸納得LRLS算法的初始化如下：

（1）在t=0時算法的初始化取：

（2）對每個t≥1的零階變量取：

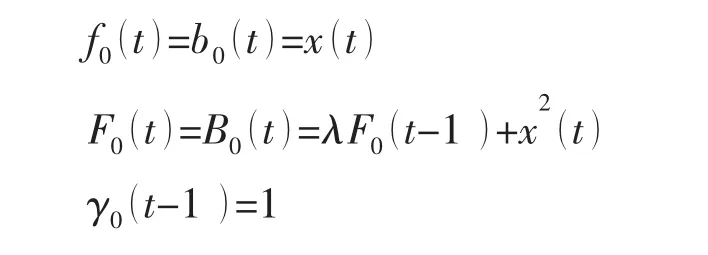
4 仿真實例

仿真所用數據為某船在90°橫浪、135°斜浪和180°頂浪航行狀態下的橫搖運動時間序列，采樣頻率為2Hz，對未來15s（即l=30步）進行預報，其預報曲線如圖2～4，擬合誤差收斂曲線如圖5所示。預報性能指標用η表示：

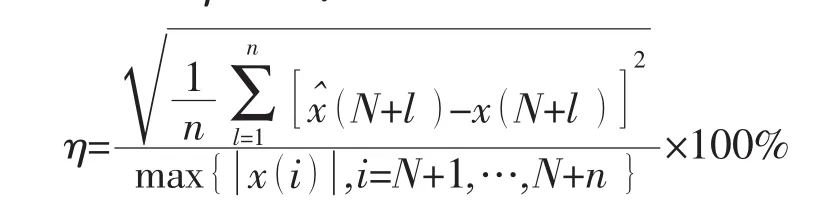
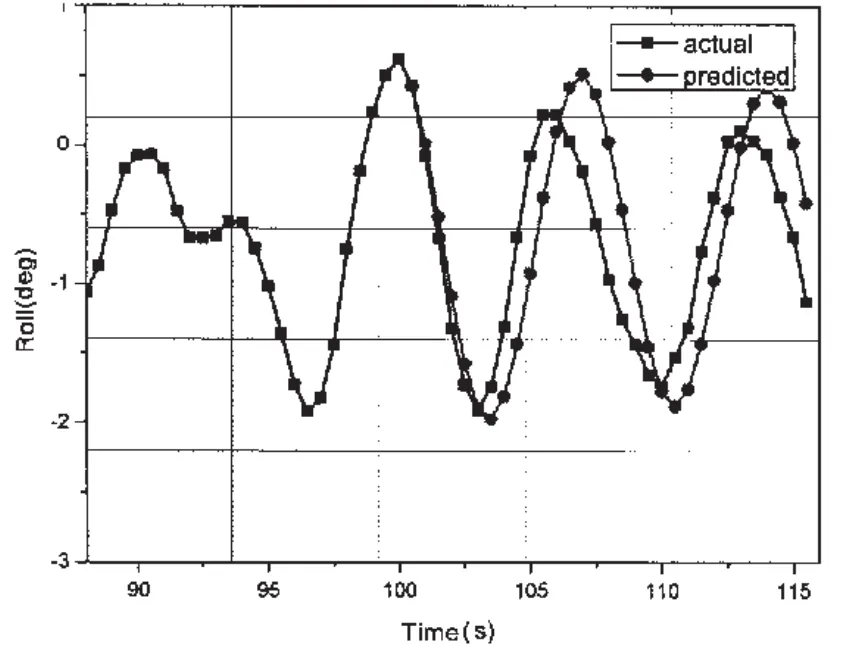
圖2 頂浪（180°）橫搖運動預報曲線Fig.2 The curve of predicted results(head sea)

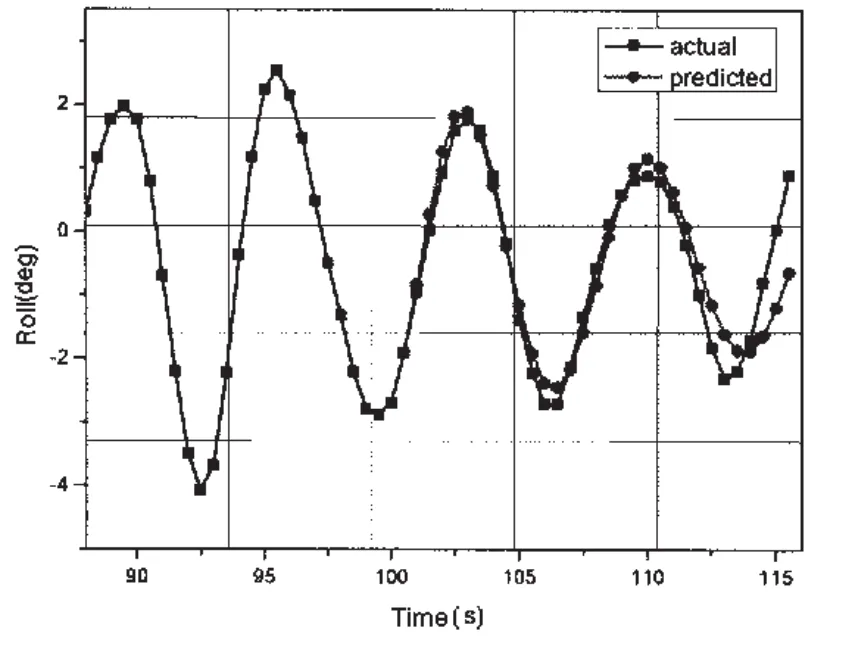
圖3 斜浪（135°）橫搖運動預報曲線Fig.3 The curve of predicted results(oblique sea)

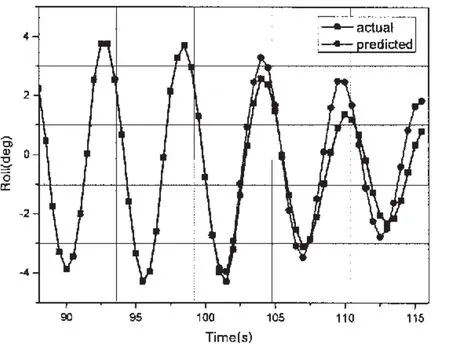
圖4 橫浪（90°）橫搖運動預報曲線Fig.4 The curve of predicted results(beam sea)

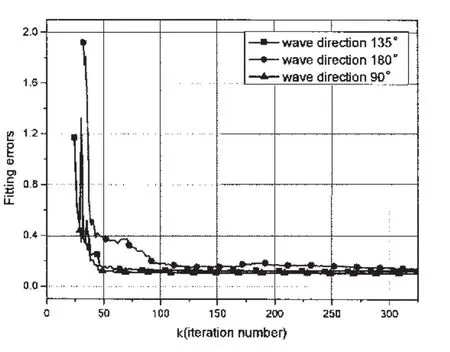
圖5 擬合誤差收斂曲線Fig.5 Convergence curves of fitting errors

由表2可以得出，基于LRLS算法的自適應AR預報模型預報效果要明顯好于RLS算法，在對斜浪（135°）的橫搖預報效果相對要好于頂浪（180°）與橫浪。隨著時間的增加，預報精度逐漸下降，尤其在橫浪工況下，橫搖預報結果的相位、幅值與實測值差別較大。由圖5可以看出，LRLS算法收斂速度較快，因而可在小樣本情況下實現自適應遞推預報。

為進一步驗證本文自適應預報模型的預報效果，利用預報精度EPA[10]來進一步對斜浪（135°）橫搖運動數據進行分析來說明基于LRLS算法的預報效果與實時預報的可行性。

表2 基于RLS、LRLS算法的AR模型預報結果Tab.2 Prediction results about AR model based on RLS,LRLS

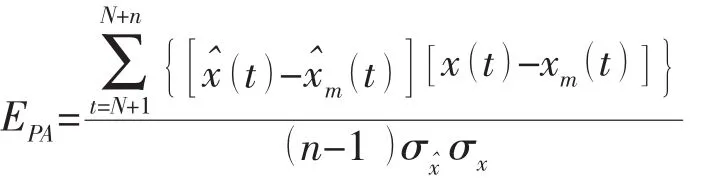
由表3可以得出，在相同工況下，對于不同的樣本數據，預報精度相差不大，隨著預報時間的增加，EPA隨預報步數逐漸減小，表明預報值逐漸偏離實測值，從而預報性能隨預報時間長度而下降，預報時間在10s時，精度仍可達0.85以上。在預報過程中，我們采用滑動窗法，即始終用200個數據遞推建立自回歸模型，預報未來15s的數據，在普通計算機上運行的時間是0.207s。遠小于采樣時間0.5s。因此在下一個新數據到來之前，未來15s的數據已經預報得到，隨著新數據的不斷到來，利用自適應算法不斷修正得到新的自回歸模型進行超前預報，從而保證所建立的自適應預報模型始終是最優的。

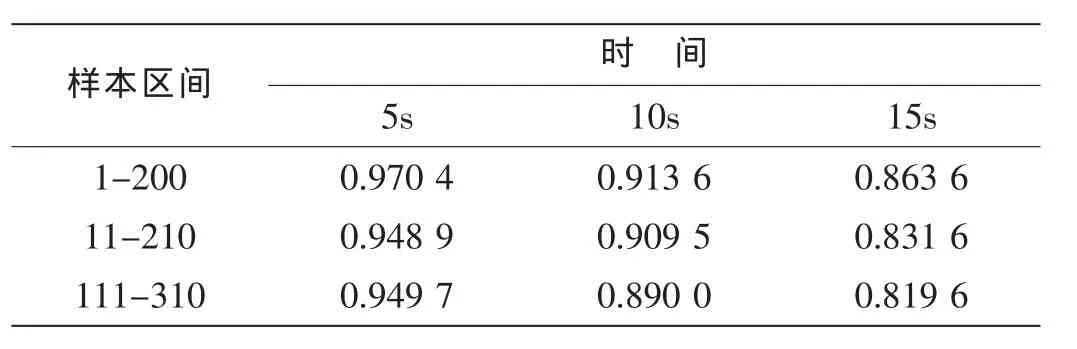
表3 預報精度EPATab.3 Prediction precision E

6 結 論

本文在RLS算法的基礎上，利用LRLS算法良好的魯棒性與收斂性，建立了基于LRLS算法的AR自適應預報模型，并將其應用到船舶運動極短期預報中。通過不同樣本數據的驗證分析，表明本文建立的自適應預報模型可有效地提高船舶運動的預報精度，并驗證了實時預報的可行性，為工程實用化提供了理論依據。

[1]楊叔子,吳 雅,軒建平,等.時間序列分析的工程應用[M].武漢:華中科技大學出版社,2007:387-396.

[2]彭秀艷,趙希人,高奇峰.船舶姿態運動實時預報算法研究[J].系統仿真學報,2007(1):267-269.

[3]趙希人,彭秀艷,沈 艷,等.艦船運動極短期建模預報的研究現狀[J].船舶工程,2002(3):4-9.

[4]馬 潔,劉小河,李國斌,等.大型艦船縱搖運動的多層遞階預報[J].船舶工程,2006,28(1):5-7.

[5]馬 潔,李國斌.船舶橫搖運動的時間序列預報[J].北京機械工業學院學報,2006,21(1):4-7.

[6]Khan A,Bil C,Marion K E.Theory and application of artificial neural networks for the real time prediction of ship motion[C].Knowledge-Based Intelligent Information and Engineering Systems.9th International Conference,KES 2005.2005,1064-9.

[7]Broome D R,Pittaras A.Ship motion prediction[C].Proceedings of the International Offshore Mechanics and Arctic Engineering Symposium,1990,1:303-311.

[8]Diniz Paulo S R著.劉郁林,景曉軍,譚剛兵等譯.自適應濾波算法與實現[M].第二版.北京:電子工業出版社,2004:96-107.

[9]楊位欽,顧 嵐編.時間序列分析與動態數據建模[M].修訂版.北京:北京理工大學出版社,1988:417-438.

[10]韓 敏.混沌時間序列預測理論與方法[M].北京:中國水利水電出版社,2007:239-241.