T型管節點抗沖擊性能研究

曲 慧，張 云，邵永波

（煙臺大學 土木工程學院，山東 煙臺 264005）

1 引 言

圓形管節點以其自重輕、造型美觀、傳力路徑明確和制作簡單等優點，廣泛應用于各種建筑工程中，如橋梁、大跨建筑及海洋石油平臺等。隨著水運、交通事業的發展，特別是“911”事件之后，由于碰撞引起的結構損傷日益受到國內外學者的關注。如2008年3月27日在建的國內第三長跨海大橋-金塘大橋遭到了貨船的撞擊，造成長約60 m，總重3 000 t的鋼筋混凝土橋面斷裂并整塊坍塌，重壓在貨船的尾部，致使4人失蹤[1]。另外，Tebbet在他的《最近五年鋼質平臺的修理經驗》一文中[2]，對世界上100起需要修理的海上平臺損傷原因，進行了分析，得到將近25%的海上平臺損傷是由于碰撞引起的。可見，在結構物受損中，由碰撞沖擊引起的破壞和損傷不容小覷。

由于撞擊為一個較為前沿的研究領域，所以目前國內外研究者對管節點的研究相對較少。Bambach等[3]對三種不同尺寸兩端固支的空心截面方鋼管梁和方鋼管混凝土梁在跨中受速度較低，質量較大的橫向沖擊力進行了試驗和非線性數值分析。計算結果與實驗結果吻合較好。金偉良[4]以某導管架結構的X斜撐在導管架安裝階段受到大噸位起重鋪管船撞擊后的損傷檢測結果為依據，對碰撞過程進行了數值模擬，按照構件模型從簡單到復雜的模擬思路得到了船舶對海洋平臺結構的撞擊力。建立了船舶與海洋平臺碰撞系統的力學模型，對導管架平臺受損構件進行了等效靜力強度計算分析。為確定受到撞擊后導管架平臺結構構件和管節點的損傷程度，提出合理可行的修理加固方案提供了分析依據。

周國寶[5]用非線性有限元技術，MSC/Dytran軟件，以中海油QK18-2導管架平臺為建模計算依據，建立了落物撞擊的數值仿模型，研究了不同撞擊速度與位置對平臺結構的撞擊力、撞擊損傷變形及能量吸收的影響，并對結構提出了改進措施。

王學蕾[6]以海洋平臺中最常見的K型節點為研究對象，用MSC/Dytran數值模擬了K型節點在撞擊荷載作用下的損傷特性，對平臺設計中常見的管節點加強措施與未加強措施的管節點進行了比較研究，研究表明采用加強筋措施效果較好。

秦立成[7]嘗試采用ANSYS/LS-DYNA顯式方法建立船舶與導管架平臺的碰撞動力分析模型，利用自動接觸算法，得出了不同情況下碰撞過程中能量轉變和平臺上層甲板中心動力響應規律，以及碰撞點最大Von mises應力和變形，并驗證了所分析結果的準確性。

從以上研究成果中可以看出，多數研究者都是針對具體工程進行的分析研究，沒有系統地對影響管節點沖擊性能的相關參數及其破壞模態進行分析。本文擬在分析幾何參數和荷載參數對管節點抗沖擊性能的影響規律基礎上，給出管節點抗沖擊性能的評價。

2 有限元模型

2.1 有限元模型的建立

結合工程實際應用和Bambach等[3]試驗構件尺寸，按照《鋼結構設計規范（50017-2003）》[8]要求，確定數值分析的典型構件，其幾何尺寸：主管100 mm×4.3 mm×600 mm、支管 70 mm×4.3 mm×300 mm；其各參數值：β=0.7、γ=23.3、τ=1、m=2 ton 和 v=1 m/s。 其中，β為支、主管的管徑比；γ為主管的徑厚比；τ為支、主管的壁厚比、m與v分別為沖擊錘的質量和速度。采用有限元軟件ABAQUS建立三維實體分析模型，如圖1所示。分析過程中，采用三維8節點實體單元（C3D8R）。

2.2 材料特性

沖擊荷載作用下的鋼管為率相關材料。本文采用Cowper-Symonds[9]模型來模擬，其動態屈服函數為：

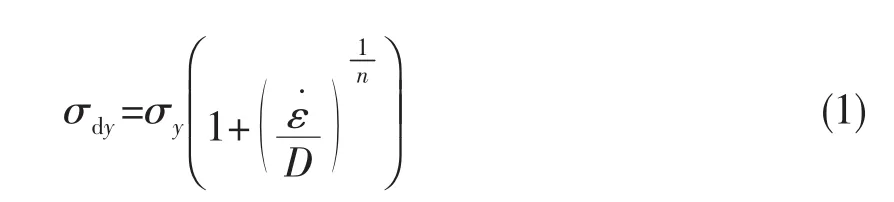
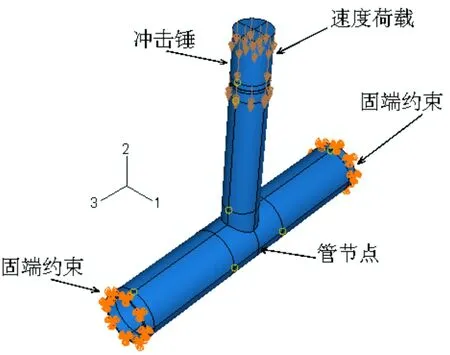
圖1 沖擊荷載下T型管節點有限元分析模型Fig.1 FEA model of T-joint under impact loading

上式中，D、n為Cowper-Symonds模型的應變率參數，其中，σdy為鋼材的動態屈服強度，σy為鋼材的靜態屈服強度，ε˙為鋼材所經歷的應變率，參考Symonds的文獻，取D＝40 s-1，n=5。本文有限元分析采用表1中鋼材的材料參數。

表1 鋼材材料參數Tab.1 Material characteristics of steel

沖擊錘取Q345鋼，因其在撞擊過程中變形很少，基本上處于彈性階段，因此在有限元模型中采用線彈性模型。為提高計算效率，用一個與支管直徑相同、高度為100 mm的圓柱體替代，對于不同質量的錘體，質量取為與實際質量相等，而密度通過換算得到。

2.3 邊界條件、荷載及界面處理

盡管實際工程中，管節點的兩端根據力學簡圖應簡化為鉸接，但結合試驗室試驗條件，并結合Bambach等[3]的試驗裝置，將管節點分析的邊界條件設定如下：主管兩端均為固支，U1，U2，U3三個自由度均被約束；支管的端部邊界為滑動支座，僅允許沿管軸方向的位移，徑向位移被約束。

本文所施加的沖擊力是通過有一定質量和速度的錘體，沿支管軸線施加在節點上。速度通過*FIELD_INITIAL_VELOCITY_TRANSLATION ONLY施加。

分析過程中，沖擊錘與端板頂面之間的接觸采用*CONTACT_SURFACE_TO_SURFACE（普通面面接觸），在FRICTION FORMULATION采用PENALTY，并設定摩擦參數為0.3。端板底面與支管端口之間，考慮到實際中兩者間采用焊縫連接的，接觸采用*CONSTRAINT_TIE_SURFACE_TO_SURFACE進行設定。

2.4 有限元分析驗證

為驗證有限元模型，對以往研究者的試驗結果進行了計算。圖2和圖3分別給出了子彈沖擊薄板和方鋼管節點沖擊試驗結果與有限元結果的比較。從圖中可以看出，無論是速度—時間關系曲線，還是沖擊力—時間關系曲線，兩者吻合均令人滿意。

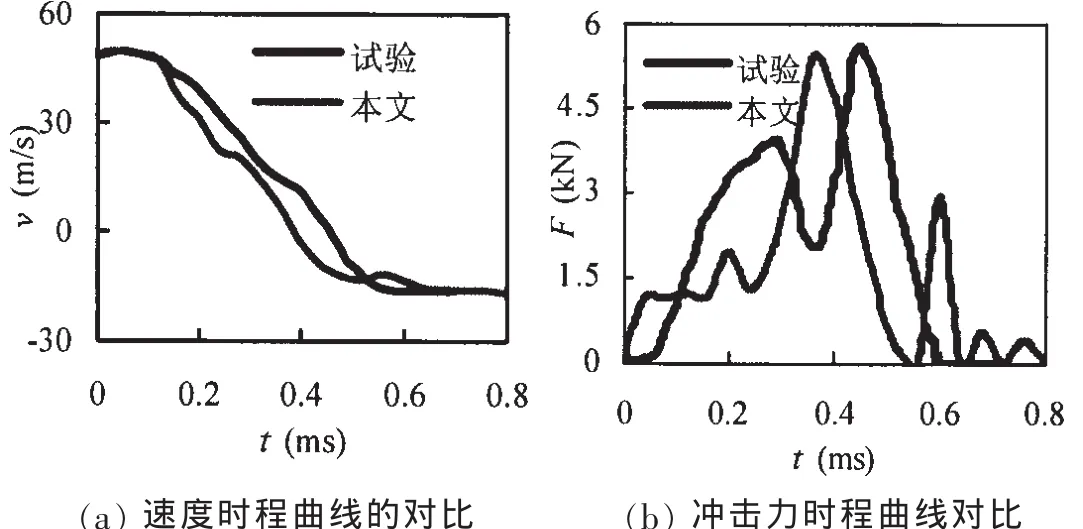
圖2 子彈沖擊圓盤試驗與計算結果比較（吳恩柏和張凌晨[10]）Fig.2 Comparison between test and FEA result for bullet experiment impact experiment

圖3 鋼管節點沖擊試驗與計算結果比較（Bambach等[3]）Fig.3 Comparison between test and FEA result for square tubular joint impact experiment

3 節點抗沖擊性能的參數分析

管節點的幾何參數對節點的抗沖擊性能有著重要的影響。在未考慮沖擊過程中其他能量損失，即理想狀態下，根據物理學公式（2）可知：

式中，I為沖量；F為沖擊力；t為接觸時間；m為沖擊錘的質量；v1為沖擊錘與節點接觸時的沖擊速度，v2為沖擊錘與節點分離時的速度。節點的抗沖擊性能與沖擊錘的物理參數m和荷載參數v有密切聯系。因此，本文分別從管節點的幾何參數（β、γ、τ）、沖擊錘的物理參數（m）和荷載參數（v）三方面，分別考查其對管節點抗沖擊性能的影響

3.1 沖擊力時程曲線

沖擊力是衡量節點抗沖擊性能的重要指標。圖4是T型圓管節點所受沖擊力與各個參數之間的時程關系曲線。

圖4 不同參數值影響下的T型管節點沖擊力時程曲線Fig.4 Time history curves of impact loading for tubular T-joint under the effect of different parameters

從圖4中可以看出，各參數均是在極短的時間內，沖擊力達到最大值，在曲線上表現為上升段陡峭，這主要是因為沖擊錘與試件瞬時接觸而引起的。各組參數中，沖擊力曲線形狀基本相似。從總體趨勢上看，沖擊力都是從零開始迅速增大，達到響應的峰值并持續一段時間后，又迅速降到零。反映在沖擊錘與管節點碰撞的全過程為：從沖擊錘接觸支管→錘與支管完全接觸→錘體速度降低→錘體被反彈起離開支管。下面分別說明各參數對管節點沖擊性能的影響：

由圖4（a）可知，在其他參數不變的情況下，參數β對管節點沖擊力有明顯影響。隨著β的增大，管節點的沖擊反力提高；碰撞作用時間隨著參數值β的增大而降低。其原因是β越大，節點剛度越大，這就使得接觸作用時間越短。再由沖量I=F·t，動量P=m·Δv，根據動量守恒定律F·t=m·Δv，得出F=m·Δv/t，在動量P相同的情況下，沖擊力與時間成反比，時間減少，力增大。但β的變化對曲線的形狀影響較小。

由圖4（b）可知，在其他參數不變的情況下，參數γ對管節點沖擊力有明顯影響。參數γ對沖擊力、碰撞作用時間變化的影響與參數β的影響規律相反。沖擊力隨參數γ值的增大而降低，但碰撞作用時間隨其增大而有所延長。這是由于γ＝D/T（其中，D為主管的直徑，T為主管的壁厚），徑厚比增大，其剛度降低，導致管節點越容易發生局部屈曲。同樣對曲線的形狀影響較小。

由圖4（c）可知，在其他參數不變的情況下，參數τ對管節點沖擊力影響相對較小。其影響規律與參數β對沖擊力大小、碰撞作用時間、曲線形狀的變化規律影響基本相似。隨著τ的增大，管節點的沖擊反力提高，碰撞作用時間隨著參數值τ的增大而降低。但總體上變化不大。

由圖4（d）可知，在其他參數不變的情況下，參數m對管節點沖擊力有明顯影響。沖擊力和碰撞作用時間均隨m的增大而增大，但曲線的形狀影響變化較小。這是由于沖擊力來自于動量，而動量是質量與速度的乘積，即P=m·Δv,在速度v不變的情況下，沖擊錘質量越大，動量就越大，產生的沖擊力也越大；對同樣的T型管節點，使其產生的變形也越大，作用時間相應延長。

由圖4（e）可知，在其他參數不變的情況下，參數v對管節點沖擊力有明顯影響，其影響規律與參數m相似，即：沖擊力和作用時間隨v的增大而增大，曲線形狀變化較小。這是由于動量是質量與速度的乘積，即P＝m·Δv，兩個變量中無論單獨變化哪個參量值，其對動量的影響都成正比，從而對沖擊力產生正比的影響。

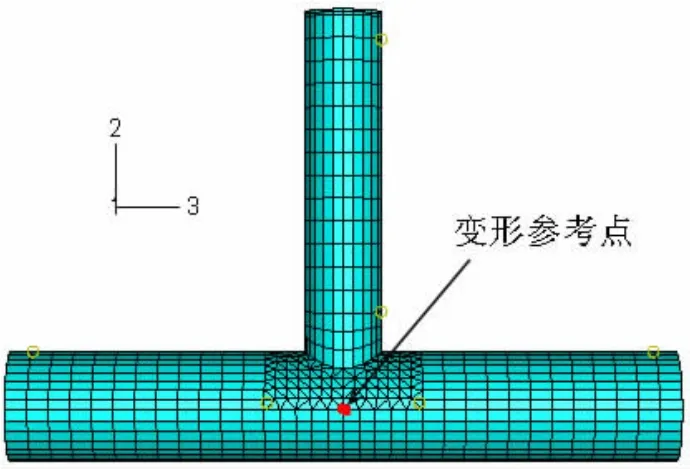
圖5 T型管節點變形分析參考點Fig.5 Reference point of deformation analysis of tubular T-joint

3.2 變形時程曲線

為考察管節點吸收沖擊能后節點的變形情況，分析過程中，本文取圖5中T型圓管節點處弦管（主管）沿1坐標軸方向變形較大點（圖5）的變形值與各個參數之間的時程關系曲線進行了分析。

通過圖6變形時程曲線，可以看出，總體上各參數的變化規律是相似的：隨著時間的變化，曲線都是首先由零開始逐漸增加到一個峰值，然后慢慢下降，最后保持在一個定值。出現這種曲線的原因主要是在沖擊力作用下的管節點，沿支管軸線方向主管下凹，同時垂直于主管和支管軸線方向側鼓，發生了彈塑性變形，隨著沖擊錘的回彈，沖擊力的逐漸消失，彈塑性變形中的彈性變形恢復，但是塑性變形是不可恢復的，從而保持不變。

圖6 不同參數值影響下的T型管節點變形值時程曲線Fig.6 Time history curves of deformation for tubular T-joint under the effect of different parameters

但是各個參數對變形時程曲線的影響規律不同，由圖6（a）可以看出，在其他參數不變的情況下，參數β對管節點變形有明顯影響。隨著β的增大，達到峰值的時間和變形峰值逐漸縮短，塑性變形也隨之變小。這是由于β越大，剛度越大，延性降低。

由圖6（b）可知，在其他參數不變的情況下，參數γ對管節點變形有明顯影響。參數γ對變形峰值、達到峰值的時間、塑性變形與參數β對管節點的影響規律相反。變形值隨參數γ值的增大而增大，達到峰值的時間隨其增大而有所延長；塑性變形也隨著γ的增大而增加。這是由于γ＝D/T，徑厚比增大，其剛度降低，越容易發生局部屈曲。

由圖6（c）可知，在其他參數不變的情況下，參數τ對管節點變形影響相對較小。隨著參數τ的增大，變形峰值、達到峰值的時間、塑性變形沒有很大變化。其原因是τ的改變對節點剛度影響不大。

由圖6（d）和圖6（e）可知，在其他參數不變的情況下，參數m和參數v對管節點的變形均有明顯影響。變形峰值、達到峰值的時間、塑性變形隨參數值的增大而增加。這是由于沖擊力來自于動量，而動量是質量與速度的乘積，即P＝m·Δv,在速度或質量不變的情況下，沖擊錘質量或速度越大，動量就越大，產生的沖擊力也越大，對同樣的T型管節點，使其產生的變形也越大，作用時間相應延長。

3.3 沖擊錘的速度時程曲線

考察沖擊錘的速度變化，能夠形象地反映沖擊過程中沖擊錘與管節點的相互作用關系。圖7為不同參數所對應的速度時程關系曲線。圖中取速度和位移向下為正，反之為負。

圖7 各參數影響下的錘體速度時程曲線Fig.7 Time history curves of hammer velocity for tubular T-joint under the effect of different parameters

從五組參數對應的錘體速度時程曲線中，可以看出，各曲線隨著時間變化，由一定初始負值，增大至零，然后繼續增至某一正值，保持恒定。其原因是，在不同參數作用下的沖擊過程中，都經歷了錘體與節點接觸時，錘體減速，速度減為零后，反向加速，直止錘體與試件分離后，速度趨于穩定。對于前三個幾何參數β、γ、τ，無論各參數值如何變化，最終速度基本趨于同一穩定值。但各個參數對達到穩定速度的時間有所不同。分別在其他參數不變的情況下，隨著參數β值的增大，該時間逐漸縮短；隨著參數γ值的增大，該時間逐漸延長；隨著參數τ值的增大，該時間沒有太大變化，基本保持不變。而后兩者參數m和v，隨著參數值的變化，最終速度各不相同。

但從速度下降的快慢程度看，沖擊速度越大則下降得越快，在曲線形狀上表現得更陡峭，這表明加速度也越大，因而沖擊力也越大。

3.4 沖擊力變形關系

對不同參數下的碰撞過程模擬得到的沖擊力與軸向變形的關系，如圖8所示。各曲線在形狀上是一致的，都近似于梯形；明顯地經歷了加載和卸載兩個階段，在卸載階段，管節點的彈性變形有所恢復，不可恢復的塑性變形表現為殘余變形。

從圖中可以看出，在各種沖擊工況下，初始時，沖擊力隨變形的增加幾乎成線性的關系；隨著試件進入塑性階段，沖擊力和變形同時達到最大值；隨后沖擊力開始緩慢下降，進入卸載階段，試件的彈性變形有所恢復，而大多數試件在卸載時的剛度幾乎與初始剛度相同，并沒有出現太大的退化。

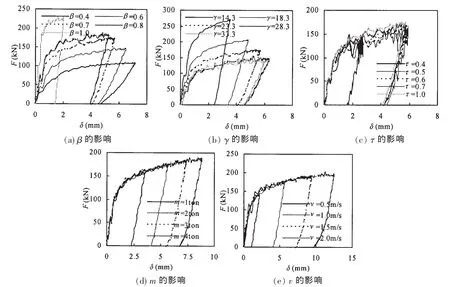
圖8 不同參數值影響下的T型管節點F-δ曲線Fig.8 F-δ curves for tubular T-joint under the effect of different parameters

由圖8（a）可知，參數γ和參數τ均保持不變時，在相同的沖擊能量下，隨著參數β值的增加，沖擊力增大，但變形減小。

由圖8（b）可知，參數β和參數τ均保持不變時，在相同的沖擊能量下，隨著參數γ值的增加，沖擊力減小，變形增大。

由圖8（c）可知，參數β和參數γ均保持不變時，在相同的沖擊能量下，隨著參數τ值的增加，沖擊力與變形均沒有很大變化，曲線形狀基本相似。可見，參數τ值不是影響沖擊性能的主要因素。

由圖8（d）和圖8（e）可知，幾何參數β、γ、τ均保持不變時，隨沖擊能量的增大，管節點所受到的沖擊力的大小和管節點的徑向變形都有增大。但節點的軸向變形增大比沖擊力的增加明顯，也就是說試件通過進一步的變形耗散了更多的能量，表現出了良好的變形性能，具有很好的延性。

3.5 耗能分析

為考察管節點的耗能能力，取圖8中沖擊力—變形曲線所包圍的面積為管節點在沖擊過程中所吸收的能量。圖9給出了各參數影響下各節點的能耗比較。從圖中可以看出，對管節點的幾何參數，在相同的沖擊能下，除β=1、γ=14.3、τ=0.4因支管局部屈曲之外，只有在β影響下，管節點的耗能能力隨著β的增大而略有提高；在γ、τ影響下，管節點的耗能能力變化不大。對相同幾何尺寸的管節點，隨著沖擊能的增大，即m、v的增大，節點的耗能也隨著成比例增大。

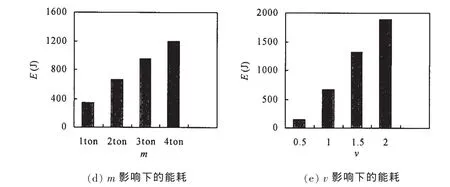
圖9 不同參數影響下T型管節點耗能比較圖Fig.9 Energy consumption curves for tubular T-joint under the effect of different parameters

4 結 論

本文運用非線性有限元方法分析不同支、主管的管徑比β；主管的徑厚比γ；支、主管的徑厚比τ、沖擊錘的質量m、速度v等參數對節點抗沖擊性能的影響，得到如下結論：

（1）支管與主管外徑比β=d/D對管節點沖擊力學性能的影響較為顯著。在相同沖擊力作用下，若節點的其它參數不變而支管與主管的外徑比在一定范圍內（0.4＜β＜0.8）增大，表現為節點剛度提高，管節點所受的最大沖擊力有所增加，沖擊力作用時間減少，總耗能略有增加，但變化不大。而β＝1.0時耗能反而減少是因為支管節點徑厚比增大，使得支管發生局部屈曲，而不是節點破壞。

（2）支管外徑與厚度比γ=D/T對管節點沖擊力學性能的影響也較為顯著。在相同沖擊力作用下，若節點的其它參數不變而支管徑厚比在一定范圍內（18.3＜γ＜33.3）增加，管節點所受的最大沖擊力減少，沖擊力作用時間隨之所增加，但總耗能變化幅度并不太明顯。對于γ＝14.3時耗能和其他相差太大是因為主管支管壁厚較大，節點的剛度很大，相同的沖擊能量不足以使之破壞。

（3）支管與主管外徑比τ=t/T對管節點沖擊力學性能的影響不太明顯。在相同沖擊力作用下，節點的其它參數不變而支管與主管的厚度比在一定范圍內增大，管節點所受的最大沖擊力、沖擊力作用時間以及總耗能變化幅度均無太大變化，這與鄭秋在鋼管混凝土短柱抗沖擊性能實驗研究及有限元分析一文[1]中得出結論一致：τ對抗沖擊作用影響不大。對于τ＝0.4的節點，不符合本規律是因為，支管壁太薄，發生了支管局部屈曲，而不是節點破環所致。

（4）幾何參數β、γ、τ均保持不變時，隨沖擊能量的增大，管節點所受到的沖擊力的大小、沖擊力作用時間、管節點的徑向變形都有增大。但節點的軸向變形增大比沖擊力的增加明顯，也就是說試件通過進一步的變形耗散了更多的能量，表現出了良好的變形性能，具有很好的延性。

（5）Cowper-Symonds[9]模型能較好地模擬鋼管在沖擊作用下大應變、高應變率下鋼管的力學性能；通過運用ABAQUS軟件的仿真分析表明，數值模擬是研究沖擊荷載作用下結構或構件動力響應的有效工具。

[1]鄭 秋.鋼管混凝土短柱抗沖擊性能實驗研究及有限元分析[D].長沙:湖南大學,2008.

[2]Tebbett I E.The last five year,5 Experience in steel platform repairs[C].Proeeding of 19th Annual Offshore Technology Conference.OTC5385,1987:261-268.

[3]Bambach M R,Jama H,Zhao X L,Grzebieta R H.Hollow and concrete filled steel hollow sections under transverse im-pact loads[J].Engineering Structures,2008,30(10):2859-2870.

[4]金偉良,宋 劍,龔順風.船舶與海洋平臺撞擊的荷載模擬[J].計算力學學報,2004,21(1):26-32.

[5]周國寶,王 林.沖擊載荷作用下海洋平臺的數值仿真研究[J].中國海洋平臺,2007,22(2):18-27.

[6]王學蕾,張延昌,王自力.海洋導管架平臺K型節點碰撞性能研究[J].江蘇科技大學學報,2007,21(4):1-6.

[7]秦立成.海洋導管架平臺碰撞動力分析[J].中國海上油氣,2008,20(6):426-419.

[8]中華人民共和國國家標準.鋼結構設計規范（GB50017－2003）[S].北京:中國計劃出版社,2003.

[9]Symonds P S.Survey of methods of analysis for plastic deformation of structures under dynamic loading[R].Brown University,Division of Engineering Report,BU/NSRDC/1-67,1967.

[10]吳恩柏,張凌晨.剛性彈體沖擊之質量效應[C]//中國臺灣第十七屆力學會議.中國臺北,1993:927-933.