基于MHMM模擬電路早期故障診斷

朱鳳波，吳文全，楊 華

(海軍工程大學，武漢 430033)

0 引言

模擬電路的故障診斷始于20世紀60年代，理論研究是從網絡元件參數可解性開始的，常用的有故障字典法和參數辨識法，但電路故障的多樣性、元件的容差及結構的復雜性，使得模擬電路故障診斷發展比較緩慢。20世紀90年代后，模糊理論、神經網絡以及支持向量機等智能機器學習語言開始應用于該領域，取得不錯的效果。但上述方法都是在硬故障(即元件斷路或短路)時效果明顯，軟故障需在元件變化較大時才能有效識別［8］。

隱馬爾科夫模型是一種廣泛應用于信號處理和模式識別的雙重隨機過程，具有很強的時序信號識別和分類能力，已成功應用于語音識別和人臉識別領域。按照觀測信號的性質可分為兩類:連續隱馬爾科夫模型(CHMM)和離散隱馬爾科夫模型(DHMM)［2］。文獻［3］提出將HMM應用于電路系統的狀態檢測及故障診斷;文獻［4］基于HMM具有很強的時序信號識別能力，對HMM在機電系統BIT抗虛警技術方面進行了研究，通過訓練DHMM來區分虛警與故障;文獻［5］將HMM應用于故障預測與設備退化研究。本文在以上研究成果的基礎上，嘗試將高斯混合隱馬爾科夫模型(MHMM)引入模擬電路的早期故障診斷，通過LDA(線性判別分析)方法對原始電路信號進行處理，完成降維，去除信號的冗余信息，然后通過MHMM模型對故障的類別進行判定。

1 MHMM模型

1.1 高斯混合模型模型介紹

高斯混合模型［6］(Gaussian Mixture Model，GMM)是一種常用的描述混合密度分布的模型，即多個高斯分布的混合分布。GMM本質上是一種多維概率密度函數，一個具有M個混合成分的D維GMM，可以用M個高斯成員的加權和來表示，即

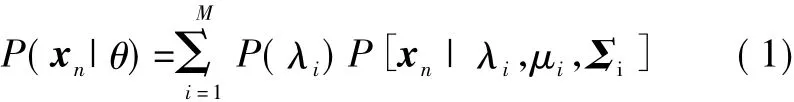
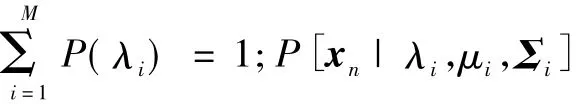
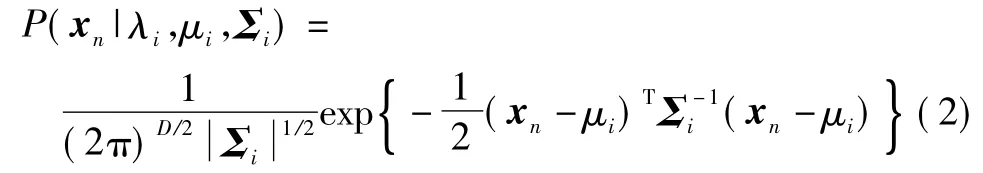
其中:μi為均值;Σi為協方差矩陣。這里共有M個高斯分布，每個函數用 λi表示，i=1，2，…，M，其參數為μi和Σi。每個函數受P(λi)加權后，取和得到xn的概率分布。

整個高斯混合模型便可以由各均值矢量、協方差矩陣及混合分量的權值來描述，因此得到一個GMM模型參數θ，表示為

1.2 MHMM模型的基本原理

隱馬爾科夫模型［3］(Hidden Markov Model，HMM)是一種基于馬爾科夫鏈發展而來的不完全數據的統計模型，它有3個基本問題需要解決:評估問題，即給定模型和觀測序列求最大似然值;解碼問題，給定模型和觀測序列求具有產生該序列最大概率的狀態序列;學習問題，給定觀測序列的訓練集估計產生該訓練集最大概率的模型。

MHMM模型［5］是常規離散HMM在觀測序列為連續密度分布信號時的一種延伸。連續密度分布的HMM模型假定被觀測的特征向量按某種概率密度分布，這種模型性能的好壞取決于假定的概率分布是否符合實際情況。一般來說，一些常用的概率分布函數很難單一地描述一組數據的分布情況，于是提出高斯混合HMM模型(Gaussian of Mixture HMM，MHMM)，即用幾個中心不同，離散度不同的高斯分布組合逼近實際的特征向量分布。

為了應用連續觀測密度，必須在模型的概率密度函數的形式上加上一些限制，來保證概率密度函數的參數以連續的方式重估。最普通的表達式為

其中:cjm為狀態j的第m個混合分量的系數，也就是混合增益因子;τ為高斯混合密度概率;μjm和Ujm分別為狀態j在第m個混合分量的均值向量和協方差矩陣。

由于高斯混合理論比較成熟，一定條件下能夠擬合任何形式的分布，因此MHMM歸結為首先用GMM方法對原始特征向量進行逼近，確定出高斯混合密度函數，然后將混合分量假定為觀測序列進行處理的一種HMM模型。

2 特征向量的提取

從電路采集的數據具有很強的冗余性和復雜性，如果直接用于HMM的訓練，不僅效果會降低，而且增大訓練的復雜程度。通過LDA技術對原始數據進行降維處理，可以提高運算速度和精度。

線性判別分析(Linear Discriminant Analysis，LDA)是一種用于分類問題的維度歸約的監督的方法，目前已被廣泛應用于人臉識別技術。它是基于Fisher準則，尋找一組將高維樣本投影到低維空間的最佳判別投影向量，使所有的投影樣本類內離散度最小且類間離散度最大，也就是在降維的同時將同一個類別的樣本盡量聚集，不同類別盡量分開［7］，即:尋找一個矩陣W，線性變換原始樣本x，使得z=WTx，且

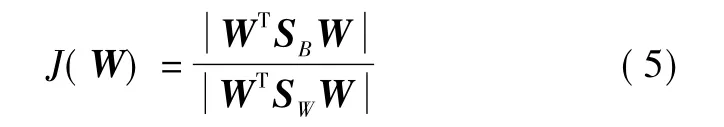
最大。式中:SB為類間散度矩陣;SW為類內散度矩陣。定義

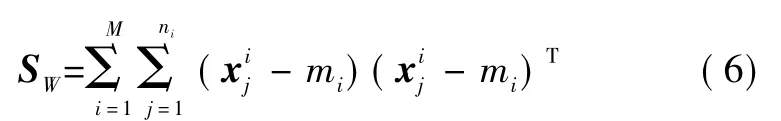
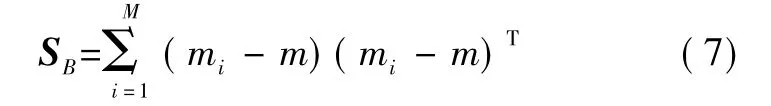
3 基于MHMM的故障診斷流程

1)特征提取。原始數據信號經LDA降維，得到低維的特征向量并且分為訓練數據和測試數據兩部分，并分別組成觀測序列。

2)模型訓練。對模型參數初始化，將不同故障狀態的特征向量訓練數據送入MHMM模型，得到不同狀態的故障模型。

3)故障辨識。將待測數據分別通過每種故障狀態模型，求出其最大似然估計值，比較該值與各訓練模型最大似然值的差值，最小者為該數據所處的故障狀態。

MHMM故障診斷流程如圖1所示。

圖1 MHMM故障診斷流程圖Fig.1 Flow chart of fault diagnosis based on MHMM

4 試驗例證與結果分析

本文實驗數據通過Multisim獲得，如圖2所示。

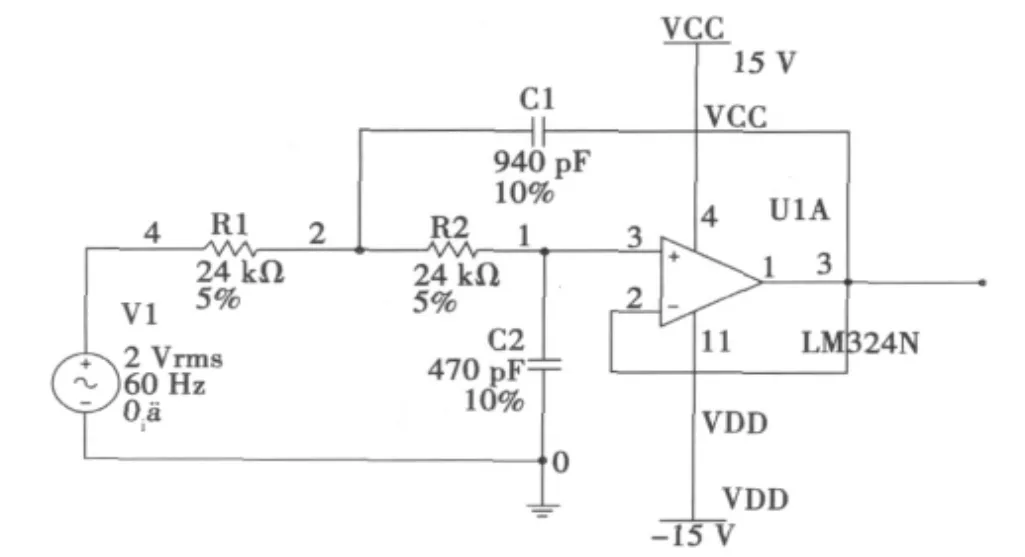
圖2 低通有源濾波器Fig.2 Circuit of active low-pass filter

圖2為有源低通濾波器，其中電阻容差為5%，電容容差為10%，通過蒙特卡羅分析，如圖3所示。

圖3 測試點蒙特卡羅分析Fig.3 Analysis of testing points based on Monte Carlo method

由圖3可見，電阻電容的早期較小變化對于10～100 kHz頻率之間影響最為明顯，因此選取100 Hz、1 kHz、10 kHz、12.5 kHz、20 kHz、25 kHz、30 kHz、40 kHz、50 kHz、80 kHz、100 kHz、125 kHz、500 kHz 對應的數值組成13維原始數據向量。設定電路有正常、R1升高10%、R1降低10%、R2升高10%、R2降低10%、C1升高10%、C1降低10%、C2升高10%、C2降低10%共9種狀態，每種狀態分別進行100次蒙特卡羅分析，得到100組原始數據向量。通過LDA算法對原始數據向量進行處理，降為5維的特征向量。如圖4所示，經LDA降維以后，取特征值最大的兩列數據作圖，可以明顯地發現，數據不僅實現了降維，而且在一定程度上對類別進行了初步的劃分。R2阻值增大與R1阻值增大基本重疊在一起，R2阻值降低與R1阻值降低也很難區分，比較符合電路的實際情況。

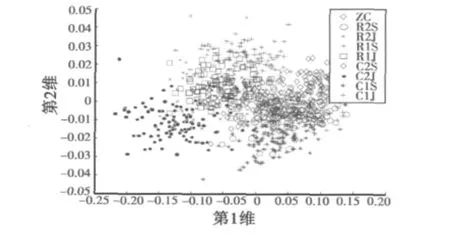
圖4 原始數據經LDA降為2維時樣本Fig.4 The sample dimension decreased by LDA

將每種狀態下的100組特征向量取50組作為訓練數據，每5組組成一個觀測序列，共10組訓練觀測序列。同樣，另外50組特征向量作為測試數據，每5組組成一個觀測序列，共10組測試觀測序列。9種電路狀態共需訓練9個MHMM模型，特征向量由3個高斯模型混合組成，HMM狀態數設為5，由電路特性確定HMM結構采用左右型［1］，初始狀態為正常，則初始矩陣為［1，0，0，0，0］，狀態轉移矩陣為［0.5，0.5，0，0，0;0，0.5，0.5，0，0;0，0，0.5，0.5，0;0，0，0，0.5，0.5;0，0，0，0，1］。GMM 高斯混合模型采用K均值法對觀測序列進行逼近［2］，確定其參數。MHMM訓練的E-M算法迭代次數［3］設為50，波動容差為1e－4，如圖5所示。

圖5 最大似然值迭代過程Fig.5 Iteration process of maximum likelihood value

圖5為其中R1升高10%時訓練的最大似然值的迭代值。

由于觀測序列的高斯逼近具有一定的隨機性，MHMM參數在一定范圍內存在波動，判定結果存在微小變動，因此采用10次結果取其平均值的做法降低這種擾動。實驗結果如表1所示。

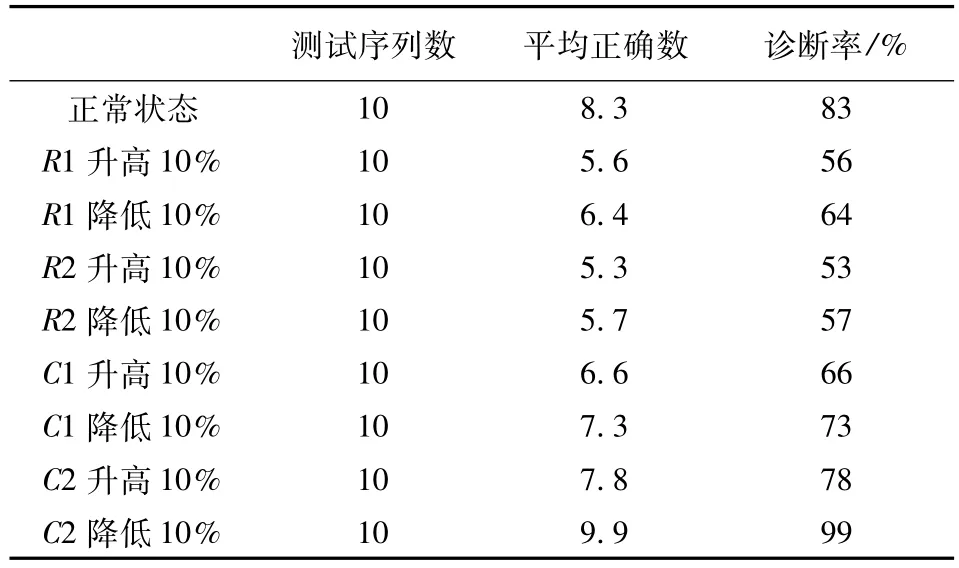
表1 MHMM故障檢測率Table 1 Diagnosis results based MHMM

由表1結果可知，MHMM模型對于故障具有較準確的判斷能力，對于混雜在一起的數據樣本(由圖4可以看出)，MHMM判斷能力有所下降，但仍然有超過50%的判斷能力(如R1、R2阻值的較小變化)，一方面是因為樣本重疊較為嚴重，另一方面從電路分析可知，該兩個電阻較小變化具有一定互補性，使特征變化不太明顯。

將相同的特征向量樣本用于BP神經網絡的訓練，設置輸入神經元個數為5，隱含層神經元個數為6，輸出神經元個數為9，網絡層數為3。通過判定，得到如表2所示結果。

由表1、表2可知，MHMM模型的判定性能明顯優于BP神經網絡，主要是因為MHMM模型使用特征向量序列進行判定，比BP神經網絡使用單個特征向量判定具有更明顯的識別能力。

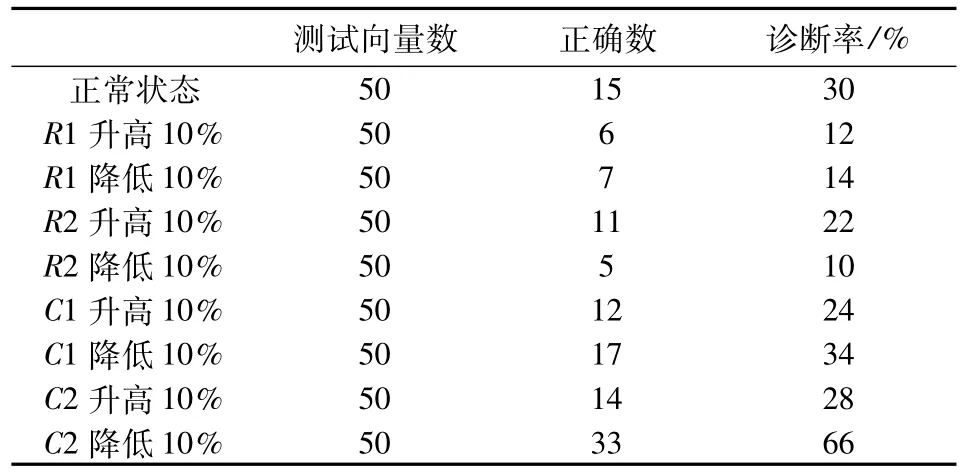
表2 BP神經網絡故障檢測率Table 2 Diagnosis results based on BP neural network

5 結論

本文提出將MHMM模型應用于模擬電子線路早期故障診斷的方法，通過實例研究了影響其性能的各種參數設置，并與BP神經網絡進行了對比，結果表明MHMM模型在模擬電路早期故障診斷中具有更好的效果，為模擬電路早期故障診斷及狀態檢測提供了一種新思路。

［1］肖元姣，蘇廣川，韓雷.基于神經網絡的電子設備故障診斷專家系統［J］.電光與控制，2005，12(3):47-49，54.

［2］ALPAYDIN E.Introduction to machine learning［M］.Beijing:China Machine Press，2009.

［3］許麗佳，王厚軍.電子系統的故障預測與健康管理技術研究［D］.成都:電子科技大學，2009.

［4］邱靜，劉冠軍，呂克洪，等.機電系統機內測試降虛警技術［M］.北京:科學出版社，2009.

［5］曾慶虎，邱靜，劉冠軍，等.基于KPCA-HSMM設備退化狀態識別與故障預測方法研究［J］.儀器儀表學報，2009，30(7):1342-1346.

［6］李春玲，鄒北驥.雙模態情緒強度估計方法研究［D］.長沙:中南大學，2008.

［7］張阿妞，莊哲民.基于優化的LDA與神經網絡人臉識別方法研究［D］.汕頭:汕頭大學，2007.