雷達機動目標跟蹤的卡爾曼粒子濾波算法

鄭潤高， 張安清

(海軍大連艦艇學院信息與通信工程系，遼寧大連 116018)

0 引言

雜波環境下雷達機動目標跟蹤問題主要是解決系統的非線性非高斯問題［1］。目前非線性算法主要有擴展卡爾曼濾波(EKF)，不敏粒子濾波(UKF)，粒子濾波(PF)。研究表明EKF、UKF只能適用非線性較弱的系統［2－3］。PF通過大量粒子表征狀態概率密度的連續Monte Carlo方法，能夠適應較強的非線性非高斯環境［3－4］，但是穩定性不高、實時性差。文獻［5 －7］的不敏粒子濾波算法(UPF)與PF相比加入了粒子狀態協方差信息，需要的粒子數更少且精度比粒子濾波更高。由于需要對每個粒子狀態進行采樣，計算復雜性仍然較大，且在跟蹤起始階段收斂較慢。本文引入卡爾曼粒子濾波(KPF)［8－10］算法，較好地解決了精度與實時性兼容以及算法收斂性問題。

1 卡爾曼粒子濾波算法

兩坐標雷達系統下，目標狀態轉移方程及觀測方程為

其中vk－1和wk分別表示過程噪聲與量測噪聲。雷達量測信號zk包括目標的距離、仰角，而目標狀態xk=［rxvxaxryvyay］′，系統非線性較強。

與UPF算法相似，KPF算法在PF算法的基礎上，考慮每個粒子的狀態及狀態協方差并由此得到粒子狀態估計，近似得到目標狀態的先驗分布，再經過粒子的重要性密度計算得到目標狀態后驗概率密度。對于已起始航跡的雷達機動目標KPF算法過程如下。

1)初始狀態采樣得到粒子為

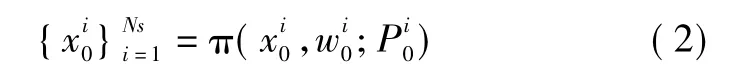
2)粒子狀態及協方差預測為

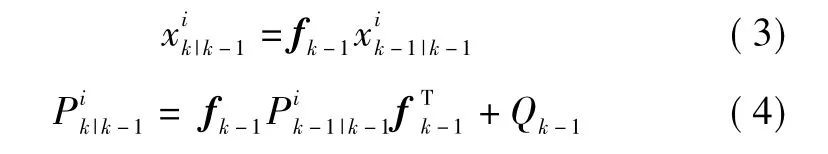
3)將極坐標下觀測數據轉換為直角坐標數據為

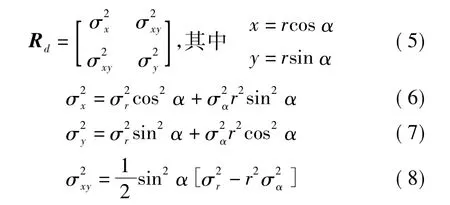
其中:r2和為距離和仰角量測噪聲方差;Rd為轉換得到的量測信號方差。

4)計算卡爾曼濾波增益為

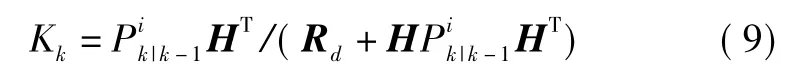
5)計算粒子狀態及協方差估計為

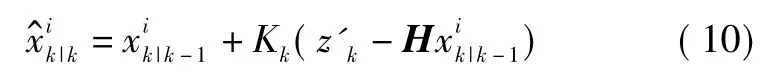
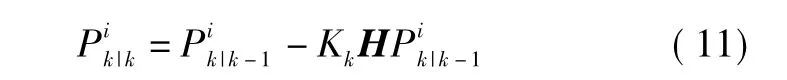
6)根據粒子狀態及協方差再采樣得到新的粒子為

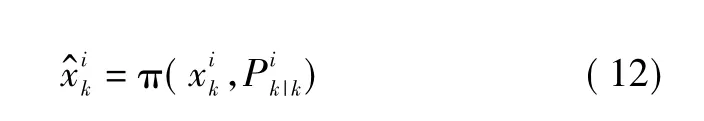
7)計算粒子似然概率、先驗轉移概率和推薦分布概率，得到重要性密度。

①似然概率為

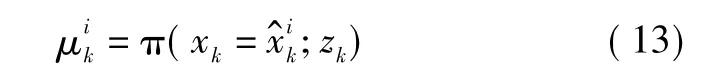
②先驗轉移概率為

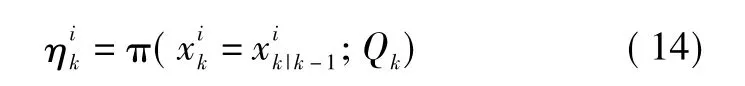
③推薦分布概率為

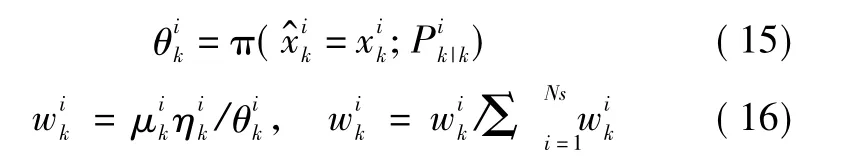
8)根據重要性密度重采樣得到新的粒子權重集，權值歸一化。

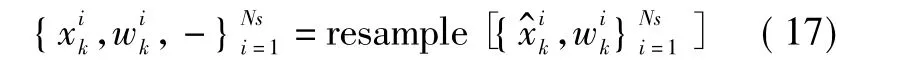
9)重復步驟2)。

相比較PF、UPF而言，KPF算法的計算量小很多，而實驗表明KPF需求的粒子數很小(在接下來的仿真分析中將會給出)。圖1是這3種算法的流程圖比較。

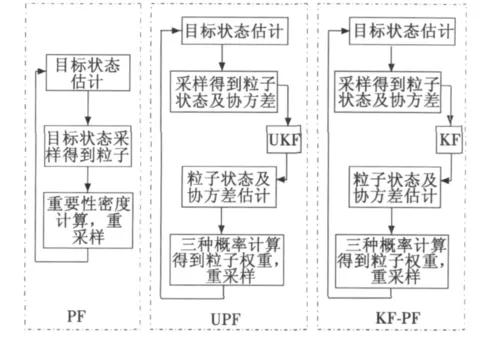
圖1 PF、UPF、KPF 算法流程圖Fig.1 The flow chart of PF，UPF and KPF algorithms

2 仿真比較分析

模擬艦艦導彈二維空間飛行的幾種方式:“俯沖機動”、“蛇形俯沖”、“轉彎機動”作為實驗驗證數據。3種算法所使用的目標運動模型都為“當前”統計模型［11］。設定機動頻率 α=1/40，加速度(單位 m/s2)上下限為［－40，40］，雷達掃描周期 T=0.1 s，觀測噪聲方差為 Rr=diag(［4020.0052］)，根據式(5) ～ 式(8)得到直角坐標系下的觀測噪聲方差陣Rd。目標狀態初始值設為X0=［x00 0 y00 0］，x和y為極坐標觀測值轉換得到的直角坐標值。

實驗中粒子數分別選擇200、100、50，對算法的3種性能:最小均方誤差(RMSE)、濾波時間和魯棒性(如果發散則前兩項無意義)進行10次Monte Carlo仿真。仿真環境為奔騰(R)4 CPU，2.4 GHz，512 M 內存。

2.1 仿真實驗1

實驗1目標俯沖機動，模擬艦艦導彈俯沖掠海飛行，總時長為91 s。18～80 s目標俯沖，迅速降低高度，其余時段直線運動。目標從開始俯沖到俯沖結束，加速度變化很快，非線性很強。這段時間有利于導彈擺脫雷達的跟蹤，因此實際裝備首先要考慮的是算法的實時性。由圖2b可以看出兩種算法在俯沖機動階段的誤差相差不大，而且起始階段KPF算法收斂更為迅速。

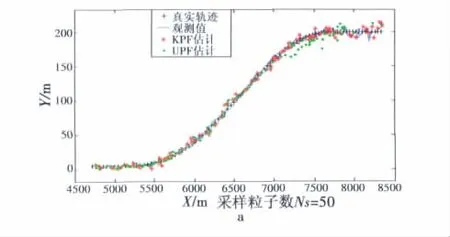
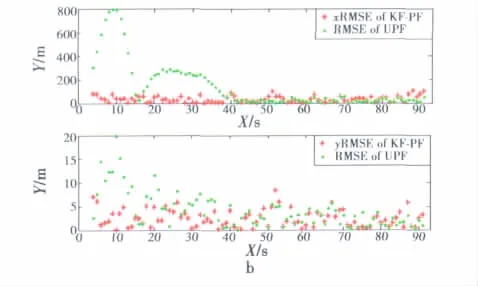
圖2 UPF、KPF算法跟蹤俯沖機動目標性能比較Fig.2 Comparison between UPF and KPF in tracking the diving targets

2.2 仿真實驗2

實驗2目標蛇形機動，掃描時長370 s，13～360 s目標蛇形機動。整個階段目標加速度變化大。因此跟蹤系統的非線性非常強，對濾波器的非線性適應能力要求很高。圖3a是兩種算法的跟蹤效果，圖3b是算法的最小均方誤差比。UPF捕捉目標機動所需時間較KPF算法要長30 s之多，而在穩定跟蹤階段，精度只比KPF高10%左右，KPF算法仿真時間是UPF的1/5。

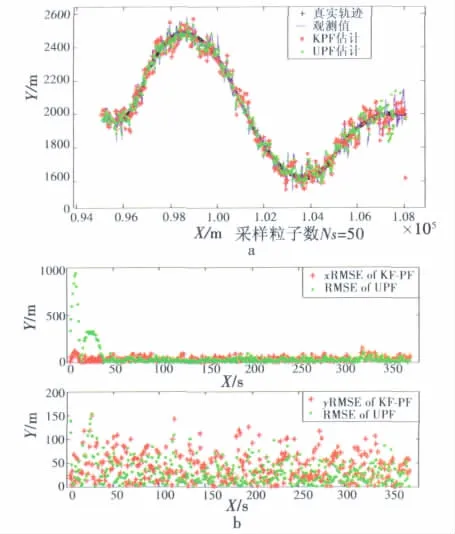
圖3 UPF、KPF算法跟蹤蛇形機動目標性能比較Fig.3 Comparison between UPF and KPF in tracking the snaking targets

2.3 仿真實驗3

實驗3目標轉彎運動，總時長為100 s，算法跟蹤效果如圖4a所示。轉彎機動非線性很強。兩種算法跟蹤效果誤差如圖4b。轉彎過程中，KPF算法能夠迅速跟蹤上目標，而UPF算法需要較長的時間才能收斂。

表1～表3列出了各跟蹤參數條件下UPF、KPF跟蹤“俯沖機動”、“蛇形機動”和“轉彎機動”目標的性能指標。根據仿真結果得出結論:

1)UPF算法跟蹤機動目標的穩定性不如KPF，目標一旦機動需要較長時間才能收斂，而KPF算法所需的時間大大少于前者;

2)UPF算法計算量是KPF的5倍左右，而精度不能高出很多;

3)KPF算法在提高運算速度(減少粒子數)的同時精度并沒有下降很多。

因此跟蹤非線性機動目標，KPF算法有以下優點:

1)計算復雜度小，是UPF計算量的1/5左右;

2)濾波精度相較于PF、EKPF要高，比UPF只低6%左右;

3)穩定性比UPF要好，能夠快速地檢測出目標的機動并跟蹤上目標的航跡。

圖4 UPF、KPF算法跟蹤轉彎機動目標性能比較Fig.4 Comparison between UPF and KPF in tracking the swerving targets

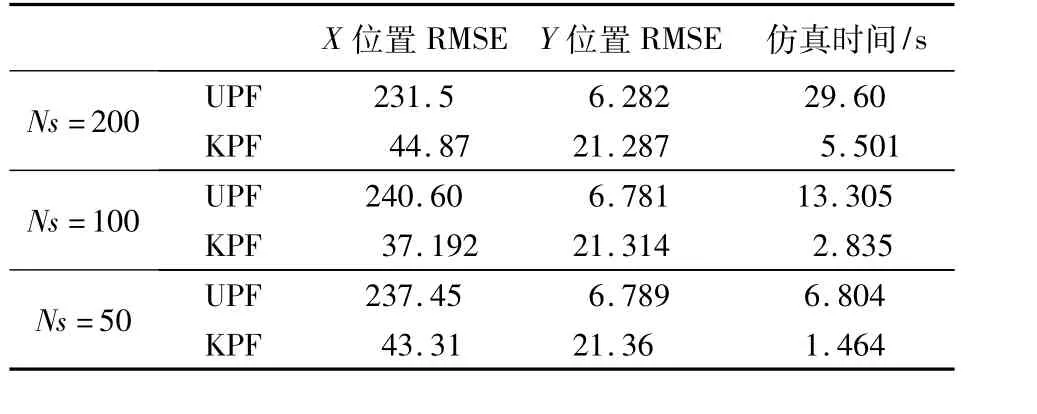
表1 俯沖機動目標跟蹤效果對比(采樣粒子數分別為200、100、50)Table 1 Comparison between UPF and KPF in tracking the diving targets(number of particles were 200，100 and 50)

表2 蛇形機動目標跟蹤效果對比(采樣粒子數分別為200、100、50)Table 2 Comparison between UPF and KPF in tracking the snaking targets(number of particles were 200，100 and 50)

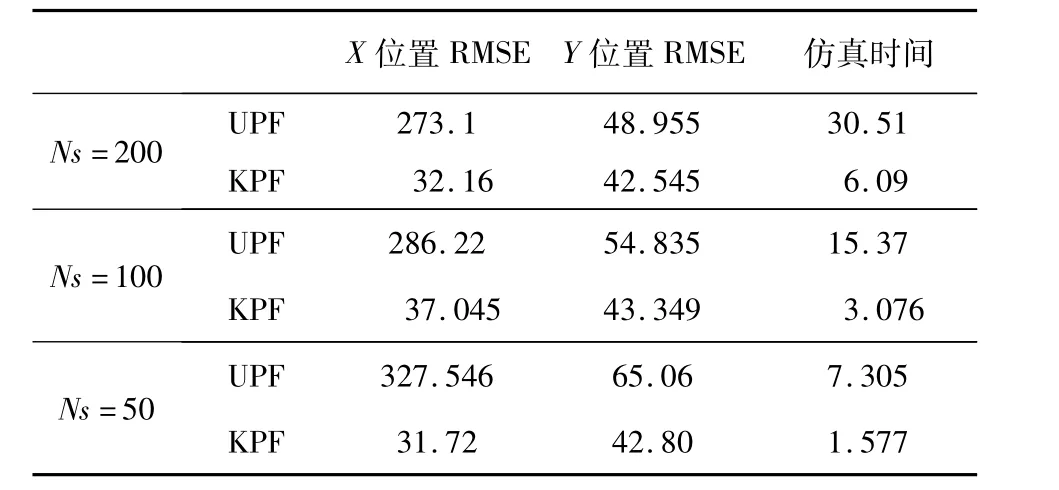
表3 轉彎機動目標跟蹤效果對比(采樣粒子數分別為200、100、50)Table 3 Comparison between UPF and KPF in tracking the swerving targets(number of particles were 200，100 and 50)

3 總結

本文基于仿真實驗中發現PF算法對二維機動運動目標濾波發散，UPF算法跟蹤機動目標的穩定性和實時性差的現象，引入了一種結合卡爾曼算法與粒子濾波算法的快速機動目標濾波跟蹤算法，是一種計算量小、跟蹤穩定性好、精度較高的混合線性/非線性濾波算法。首先通過坐標轉換將極坐標觀測數據轉換為直角坐標數據(包括量測噪聲陣的轉換)，然后通過卡爾曼濾波算法近似得到粒子狀態的先驗概率估計，然后應用粒子濾波的方法得到目標狀態后驗概率分布。仿真實驗表明該算法具有較高非線性快速機動目標跟蹤的費效比，對實現復雜電磁環境下快速機動目標的跟蹤具有一定的應用價值。

［1］ SHALOM Y B，DAUM F，HUANG J.The probabilistic data association filter:Estimation in the presence of measurement origin uncertainty［J］.IEEE Control Systems Magazine，2009(9):82-100.

［2］ ARULAMPALAM M S，MASKELL S.A tutorial on particle filters for online nonlinear/non-gaussian bayesian tracking［J］.IEEE Transactions on Signal Processing，2002，50(2):174-188.

［3］ DOUCET A，GODAILL S.On sequential Monte Carlo methods for Bayesian filtering［J］.Statistics and Computing，2000(10):197-208.

［4］ QI Cheng，BONDON P.A new unscented particle filter［C］//Acoustics Speech and Signal Processing of IEEE International Conference on ICASSP，2008:3417-3420.

［5］ LANCASTER J，BLACKMAN S，YU L，et al.IMM/MHT tracking with an unscented particle filter with application to ground targets［J］.Proc.of SPIE，2007，6699:19-22.

［6］ PAYNE O.An unscented particle filter for GMTI tracking［C］//IEEE Aerospace Conference Proceedings，2004:1869-1875.

［7］ NI Bingbing，WINKLER S，KASSIM A A.An efficient stochastic framework for 3D human motion tracking［C］//Proc.of SPIE-IS＆T Electronic Imaging，2009，6805:1-10.

［8］ MANDEL J，BEEZLEY J D.An ensemble kalman particle predictor-corrector filter for non-gaussian data assimilation［C］//ICCS 2009 Proceedings of the 9thInternational Conference on Computational Science，2009:470-478.

［9］ LOSSE H，FRANKE U，STILLER C.Kalman particle filter for lane recognition on rural roads［C］//IEEE Intelligent Vehicles Symposium，2007:60-65.

［10］ 徐劍，畢篤彥.基于卡爾曼濾波和粒子濾波級聯模型的靜基座慣導初始對準算法及仿真［J］.電光與控制，2006，13(1):27-32.

［11］ ZHOU Hongren，KUMARF K S P.A“Current”statistical model and adaptive algorithm for estimating maneuvering targets［J］.AIAA Journal of Guidance，1984，7(5):596-602.