基于多回路擴張狀態觀測的加筋壁板結構多模態振動控制

李生權，裘進浩，季宏麗

(1.揚州大學 能源與動力工程學院，揚州 225127;2.南京航空航天大學 機械結構強度與振動國家重點實驗室，南京 210016)

加筋壁板由于具有剛度大、節省材料等特點成為飛機蒙皮結構中的典型形式。飛機飛行時易受到發動機、外部激勵擾動等因素的影響，引起壁板結構發生很大幅度的振動。壁板結構的長期大幅度振動可能會引起疲勞裂紋、結構破壞甚至造成重大事故的隱憂。所以對其進行振動控制，就顯得格外的重要。為此，國內外學者對加筋板結構振動問題進行廣泛的研究［1－3］。

壓電智能加筋壁板結構是在不改變加筋板基體結構強度特性的基礎上，將壓電元件粘貼到基體結構中組成的一種智能結構。這種壓電智能結構不僅同時具有傳感和驅動功能，還具有優良的機電耦合特性、質量輕和可靠性高等特點，是行之有效的振動控制備選結構之一。并在航空航天領域取得了一定的成果，尤其是與振動主動控制技術相結合，在結構的減振降噪方面表現出良好應用前景，引起了越來越多的關注［4］。

與一般的板結構不一樣，加筋壁板是由加強框、長桁和鉚釘等組成的復雜結構，具有剛度大，存在多種不確定性和耦合等特點。這是由于在實際環境中壓電加筋壁板結構多是具有多重干擾激勵影響的系統，這使得結構成了一個多變量耦合的不確定非線性系統;這些因素給加筋壁板結構的振動主動抑制帶來了很大挑戰。目前壓電智能加筋壁板結構主動振動控制大多采用速度負反饋和LQR等基于嚴格數學模型的線性控制策略［5－6］，盡管這類控制器具有結構簡單，容易實現等優點，但是實際結構的數學模型難以精確建立，則振動抑制的性能非常有限。

微電子技術尤其是微控制器技術的發展為現代控制理論和新型振動主動控制算法的實現提供了應用平臺，近年來出現了一些新的非線性控制振動控制算法，如基于神經網絡前饋補償的控制方法［7］，基于滑模變結構的控制方法［8］，基于模糊邏輯的控制方法［9］。這些方法不僅豐富了智能結構的控制理論，而且從不同的方面使得壓電智能結構的振動抑制性能得到了改進。但是，在多模態控制時，這些主動控制方法沒有完全考慮結構多模態的輸出疊加和控制信號耦合等特性，難以滿足多模態振動抑制性能的要求。

自抗擾控制器［10－11］(ADRC)能實時估計和補償對象模型攝動和外部干擾激勵等內外擾動，并結合非線性狀態反饋的一種實用的控制系統非線性綜合方法，而被廣泛的應用到各種機械系統［12－13］。但是，將自抗擾控制技術應用到壓電智能壁板結構的多模態振動控制卻是一個全新的課題。自抗擾控制器本來是針對對象模型未知的一類非線性的控制策略，為了算法簡單，在實際應用中，將ADRC簡化成了線性反饋結構，國內外學者大量的應用研究表明線性反饋結構的ADRC(LADRC)依然對非線性對象有很好的控制效果［14－16］。

為了克服四面固支加筋壁板結構難以建立精確數學模型，以及多模態控制時多變量耦合的特性，提出基于多回路擴張狀態觀測器(multi-loop ESO)解耦控制的線性自抗擾多模態振動控制策略。這種方法的基本思想是:首先，將各個模態之間的耦合(包含輸出疊加和控制信號的相互影響)看作為當前控制模態的廣義干擾量。用線性擴張狀態觀測器(LESO)對各個子系統的耦合、外擾和模態參數變化等不確定作用進行動態估計，并且將LESO的估計值引入到反饋控制器中進行補償，實現了多模態的解耦;其次，由于其他模態的影響已經去除，則可以按照SISO的LADRC方式，方便的設計各個獨立模態的反饋控制策略。由于LESO準確快速的估計了結構動態特性和各種擾動，則LADRC能夠成功的控制結構的多模態振動。而且，多模態LADRC不依賴模態結構的數學模型，則系統具有較強的魯棒性能。為了驗證該多模態振動控制策略的有效性，基于dSPACE實時仿真試驗系統，對ARJ21型飛機靠近尾部的加筋壁板結構進行了多模態控制實驗。

1 四面固支壓電智能板結構的機電模型

本文研究的是粘貼有壓電元件的四面固支的加筋壁板結構，如圖1所示，并且背面同位配置相應的壓電片。盡管板結構是無窮自由度的，但在某階共振頻率附近發生振動時，可以用只有單個自由度的質量阻尼彈簧系統來描述其機電耦合模型。在加筋壁板結構的多模態主動振動控制過程中，由于需要較大幅值的控制信號，則各個控制壓電片輸出的模態控制力會相互影響;并且在壓電加筋板結構中，傳感壓電片輸出的各階模態位移也存在輸出疊加。

圖1 壓電智能加筋板結構Fig.1 Piezoelectric stiffened plate structure

與文獻［17］相似，典型的壓電智能結構簡化成如圖2所示的機電耦合系統。但是，與文獻［17］不同的是，這里不僅考慮結構的二階模態振動疊加［18］，而且考慮各階模態控制量之間的相互影響。

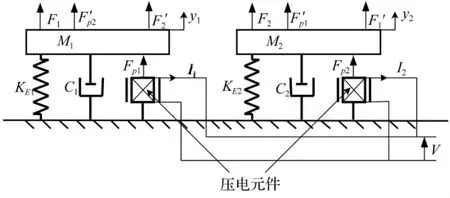
圖2 壓電智能結構多模態機電模型Fig.2 Diagram of electromechanical model

假設包含壓電元件的整個結構具有線彈性，結合圖2，得到整個智能結構的耦合動力學方程為:

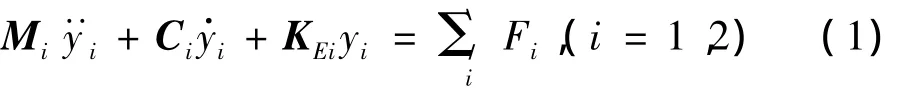
式中:Mi，Ci和KEi分別表示結構的模態質量、阻尼和剛度;yi為模態質量位移;ΣiFi表示外界作用力總和，一般包含有外界激勵干擾Fei和壓電元件的控制作用Fpi，其它模態激勵干擾Fei和控制壓電元件F'pi的耦合作用，其中F'ei體現了結構振動的輸出疊加因素，而F'pi表示各個模態之間控制輸入的相互影響。考慮壁板結構上粘貼壓電元件，則整個結構的驅動方程和傳感性能為:

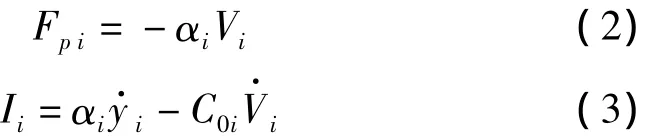
式中:Vi和Ii分別是壓電元件的施加控制電壓和流通電流，αi是力因子，C0i是壓電元件的受夾電容。從而動力學微分方程(1)被重新寫成:

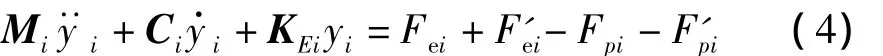
結構的各項參數為:

其中:f0i，f1i分別為壓電元件短路和開路時某階共振頻率，它的測量準確性與壓電片布置的方式和粘貼用環氧樹脂層的均勻程度等都有很直接關系;εi為壓電元件開路時板的阻尼比;λi表示壓電元件開路電壓與固支板測量點模態位移之比。

2 壓電加筋壁板結構的多模態線性自抗擾振動控制器設計

一般而言，實際的壁板結構的動力學方程(4)中模態質量矩陣M都是可逆矩陣，考慮雙輸入雙輸出壓電振動結構，則微分方程(4)整理為:

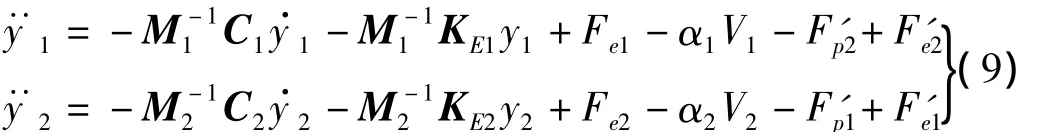
其中F'p1，F'e2分別是第二階模態控制量和激勵信號對第一階模態的影響，且分別是第二階模態控制電壓和輸出位移的函數;同理則F'p1，F'e1分別體現第一階模態對第二階模態的耦合影響。

為了方便分析LADRC的二階模態振動控制的過程，作如下定義:

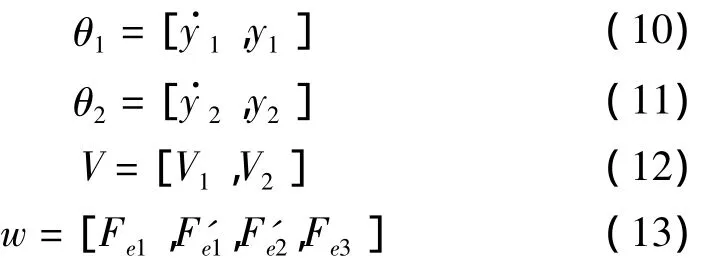
考慮耦合的輸入－輸出的關系，結合式(10)～式(13)，式(9)可寫成:

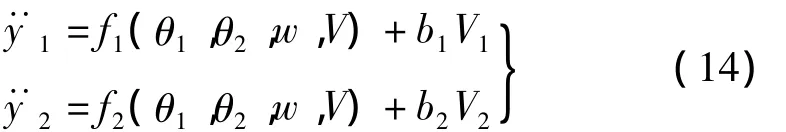
考慮到結構特點，研究用兩對壓電片分別作傳感和控制，則式(14)中的輸入和輸出個數是完全一樣的。式中函數 fi(θi，w，V)包含有 F'pi，F'ei等不確定因素作用，則函數fi無法獲得精確的數學表達式。ADRC的基本思想是，通過擴張狀態觀測器實時的估計出內擾和外擾的總和fi，則實際運用時，就無需知道fi的精確的數學表達式。

2.1 多回路擴張狀態觀測器

作為眾多結構的動態特性離線辨識策略的替代品，ESO提供了一種實時估計結構動態特性和外部干擾激勵影響的新方法。加筋壁板結構前二階模態對象是一個二輸入二輸出的耦合對象。考慮結構對象式(14)的第一階模態，基于獨立模態的LADRC振動抑制策略如下:

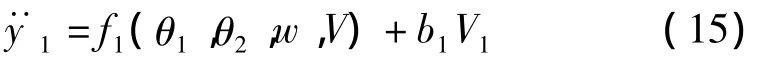
這樣一階模態能用如下狀態方程形式表示:

對應的一階模態的線性擴張狀態觀測器(LESO)為:

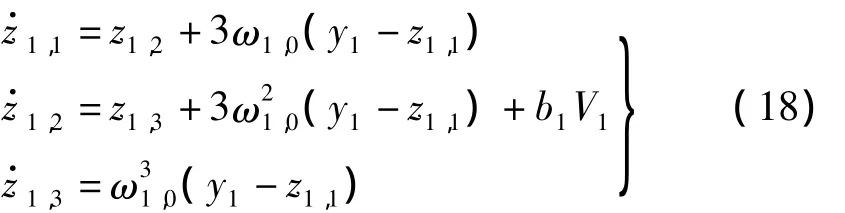
其中:z1，1，z1，2分別為一階振動模態位移和速度估計量，z1，3為廣義干擾量 f1的估計值;ω1，0為 LESO 的帶寬，一般而言，較大的觀測器帶寬能提高狀態和干擾的估計精度，但是，可能提高整個閉環控制結構的噪聲靈敏度，則必須選擇合適的觀測器帶寬ω1，0，在滿足性能要求的基礎上，盡可能的降低噪聲靈敏度。

同理，由于第一階模態對第二階模態的耦合影響都綜合到廣義干擾函數 f2(θ1，θ2，w，V)中，則第二階模態對應的線性擴張狀態觀測器(LESO)為:

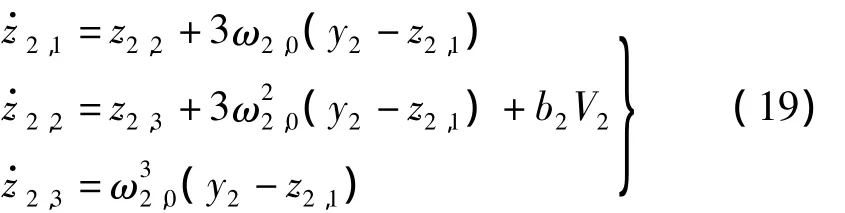
式中，z2，3為廣義干擾量f2的估計值;選擇合適的LESO帶寬，滿足估計性能要求。

2.2 多模態動態解耦控制

選擇合適的LESO的帶寬ωi，0，則觀測狀態能夠很好的估計出結構各階擴張狀態。忽略fi和zi，3之間的偏差影響，則LADRC能夠有效的補償fi，具體的控制器框圖如圖3所示。其中，

式中:kp，1和kd，1分別表示第一階模態反饋控制器的比例和微分增益。在圖3中，為第一階模態的位移設定值，加筋壁板結構第二階模態干擾激勵Fe，2和第二階模態控制信號V2對第一階模態輸出位移y1耦合環節分別為 Pe，1，P1，2，環節 Pe，1，P1，2的輸出 ye，2，y1，2看作對y1的擾動輸入，因此:

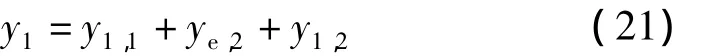
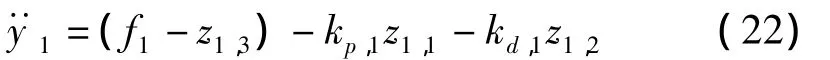
其中，f1包含了干擾激勵Fe，2和第二階模態控制信號V2對第一階模態的耦合影響。如果選擇了合適的LESO參數，上式右邊第一項是可以忽略的，則剩余項是一個簡單的PD控制器，構成了一個反饋補償項。第二階模態控制原理與第一階模態類同。這樣，就將帶有耦合的加筋壁板結構間接地解耦成了2個獨立的控制回路。實現了基于多回路LESO的多模態自抗擾策略的振動抑制。

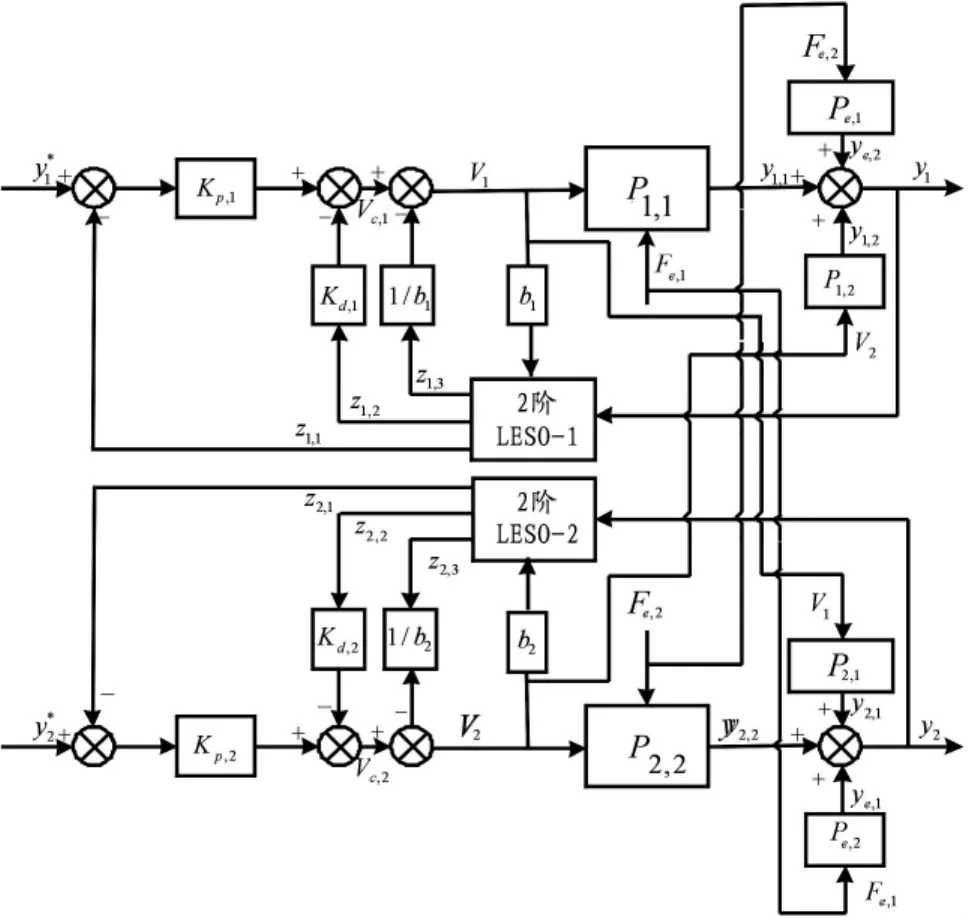
圖3 四面固支板結構多模態自抗擾振動控制框圖Fig.3 Diagram of all-clamped panel structural multi-mode vibration controller based on ADRC

3 實驗研究

3.1 實驗系統

本文以ARJ21型飛機中常用的加筋壁板結構為例，搭建了如圖4所示的實驗系統，振動對象為四面固支鋁合金LY12CZ加筋壁板結構，總體尺寸為860mm×550mm×1mm，其中包含有四根長桁將整個板結構分成9個面，在每個面的中間部位正反對稱的粘貼兩塊壓電片，壓電片的尺寸為30mm×30mm×0.2mm。考慮整個結構的前兩階共振模態，則分別中間面和左右面的壓電片有最大的應變，正上面的壓電片用來激勵板結構。整個結構的前兩階固有頻率通過實驗掃頻的方式得出，掃頻的頻帶為40～500Hz，實驗測量的前兩階的共振頻率為268.6Hz和307.7Hz。為了驗證文中提出多模態振動抑制方法的可行性，則采用同位配置的原則，分別用中間面和右邊面的對稱壓電片作傳感和控制。基于dSPACE1103系統，在MatlabR2006a/Simulink環境下，運用線性自抗擾控制策略對四面固支壓電智能加筋板結構進行主動振動抑制實驗。

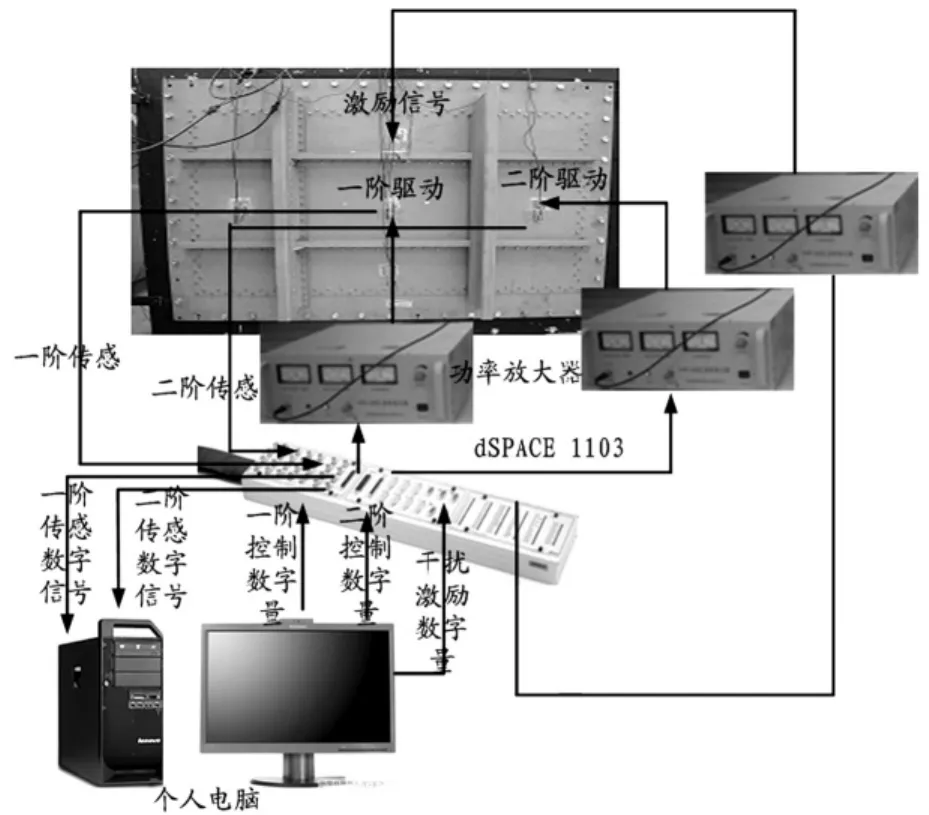
圖4 加筋壁板結構主動振動控制實驗系統Fig.4 Photograph of the experimental setup

3.2 實驗結果與分析

為了評估多模態振動自抗擾控制策略的控制性能，分別給出結構在獨立模態激勵下和多模態激勵下的實驗結果。為了公平比較，首先，都選擇正上面的外部壓電片作為激勵源;其次，一階模態(268.6Hz)控制和傳感分別選擇壓電板的中間對稱位置的內部和外部壓電片，二階模態(307.7Hz)控制和傳感分別選擇右面對稱位置的內部和外部壓電片。由于獨立模態下振動模態動力學方程是一個二階系統，根據第2.1節分析可知，只要選擇恰當LESO的觀測器帶寬ωi，0就能估計出包含其他模態耦合影響在內的各種干擾，實現了多模態的解耦控制。基于此，分別對前兩階模態進行獨立模態的LADRC振動控制器設計。其次，在進行各模態獨立控制器設計時，鑒于前兩階模態的共振頻率分別為268.6Hz和307.8Hz，根據文獻［14 －15］的方法，分別選擇這兩階模態的LESO觀測器帶寬為1600和1900，實際運用中應該在跟蹤精度和噪聲靈敏度進行折中處理，于是在這兩個值附近采用試湊法，在帶寬分別選擇1700和2000時整個系統具有最好的振動控制性能。再次，運用分離原理，且根據(22)式可知，反饋控制器等同于設計結構的速度和位移反饋控制增益，而這個過程與最優控制最后的結構形式是一致的。則根據最優控制的方式獲得了具有最優的振動抑制性能下的控制器參數，分別為:Kp，1=120，Kd，1=460，Kp，2=150，Kd，2=500。最后結合式(2)、式(5)、式(14)可知，這里力因子bi=αi是唯一與結構模型有一定關系的量。根據(5)，αi=λiCi，表示的是壓電片驅動能力的一個量，可以根據實驗測量的方法很方便的確定為b1=0.005，b2=0.003。

為了全面的了解多回路狀態觀測器LADRC的多模態的主動振動控制的性能，進行如下三類情況的主動振動控制實驗。

圖5 第一階模態LADRC振動控制性能Fig.5 Control performance of the first mode with LADRC in single-mode control

圖6 第二階模態的LADRC振動控制性能Fig.6 Control performance of the second mode with LADRC in single-mode control

第一種情況:外部激勵干擾分別是前兩階共振頻率的正弦信號。

在單模態振動控制中，功率放大器峰－峰值為80 V電壓激發某一個模態。LADRC振動控制結果如圖5和圖6所示，在控制電壓峰－峰值分別為30.5 V和35.6 V的條件下，一階模態和二階模態分別降低了13.4 dB和13.06 dB。具體的一階共振頻率和二階共振頻率峰值控制前和控制后的分貝值見表1所示。

表1 單模態線性自抗擾控制性能Tab.1 The control performance of LADRC in single-mode control

圖7 二階模態線性自抗擾的前兩階模態激勵振動抑制效果Fig.7 Performances of vibration control with LADRC in two-mode control

第二種情況:外部同時存在前兩階的共振頻率干擾激勵。

為了進行加筋壁板前兩階模態的線性自抗擾解耦振動控制，在控制過程中，選擇一階模態和二階模態激勵信號為1∶1的方式，功率放大器輸出峰－峰值為120 V電壓激發加筋壁板的前兩階固有頻率，傳感器采用同位配置的方式。加筋壁板結構的前兩階模態的頻域和時域響應如圖7所示。

從圖7(a)～圖7(d)的傳感壓電片時域和頻域響應來看，控制前后兩個傳感壓電片采集到的一階模態和二階模態的共同影響存在輸出疊加的現象。從圖7(d)可知，兩階模態的控制壓電片峰－峰值分別為40.02 V和46.76 V，對整個壁板結構而言，相當于是前兩階模態的二次激勵，存在控制耦合。圖7(a)中間壓電片所示，這種多模態LADRC對一階模態(268.6Hz)減少了15.7 dB，二階模態(307.7Hz)減少了12.4 dB;從圖7(c)右邊壓電片所示，一階模態減少12.3 dB和二階模態減少了12.6 dB。

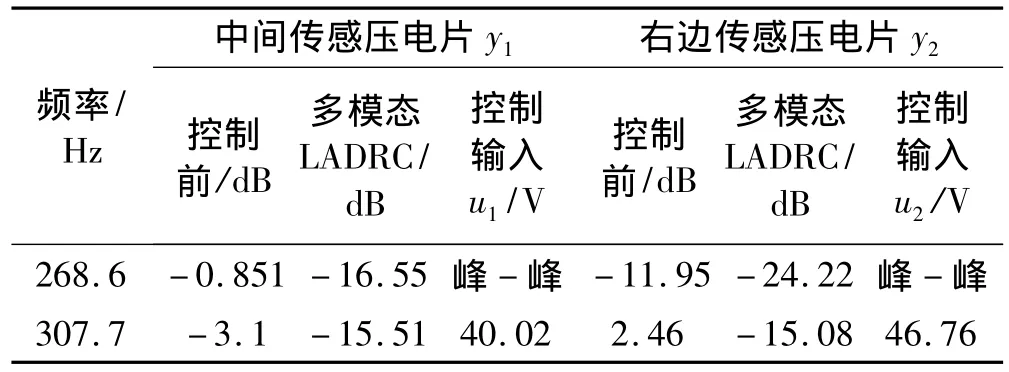
表2 多模態線性自抗擾控制性能Tab.2 The control performances of LADRC in multimodal control

在選擇多模態PD反饋控制器參數分別與單模態的參數選擇一致且控制電壓稍大的情況下，多模態控制效果幾乎跟單模態控制效果一致。這是因為多回路擴張狀態觀測器分別將其他模態的輸出和控制量的耦合影響看作是廣義干擾，并分別進行前饋補償，很好的將多模態振動控制問題轉換成單模態的線性自抗擾控制器的設計問題。并且，從圖7(a)和圖7(b)的對比可以看出，中間傳感壓電片體現的一階模態(268.6Hz)的控制效果要稍優于右邊傳感壓電片。但是，由于右邊驅動壓電片主要是針對二階模態設計的控制器，就公平而言，則右邊傳感壓電片體現的一階模態振動抑制是真實的效果。之所以存在這種大約2 dB差異，應該是由于一階模態傳感壓電片同位配置引起的局部應變等因素所致。具體的多模態LADRC振動抑制效果如表2所示。

第三種情況:外部激勵中加入帶寬隨機信號。

此例是在激勵壓電片中加入帶寬為200Hz～500Hz，幅值為［－80，80］V區間的隨機信號，與二階模態的振動控制類似，同樣選擇中間和右邊的兩對壓電片分別作傳感和控制。圖8(a)和圖8(b)分別顯示了主動控制前后檢測到的信號。從響應可知，如果沒有加入主動控制策略，兩個傳感壓電片分別采集到較大的波動，當采用這種二維控制輸入方式的多模態LADRC控制器以后，就具有低的穩態波動。當存在外部激勵擾動時，二階ESO估計擾動并把它補償到控制量中，增大穩態控制量，這樣就能獲得小的穩態波動。

幾種情況的主動振動控制表明了提出的控制策略是穩定的，并且只需要在選擇好各階單模態振動控制器的情況下，采用文中所提的多回路擴張狀態觀測器分別補償的方式，用同樣的控制器參數，不僅能獲得幾乎同樣的多模態振動控制效果，而且具有優良的抗外界干擾激勵的能力。

圖8 加入帶寬隨機干擾激勵后振動抑制性能Fig.8 Performances of vibration control with band-limited random disturbance excitation

4 結論

針對加筋壁板結構多模態主動振動抑制中存在輸出疊加和控制輸入耦合影響的問題，提出了一種基于多回路擴張狀態觀測器的多模態振動主動控制策略，分別估計出其他模態輸出和控制量的影響。這樣只需分別選擇合理的單模態二階線性自抗擾控制器參數，直接運用到加筋壁板結構的多模態振動控制中，就能獲得與單模態幾乎一樣的控制效果，簡化了多模態主動控制器的設計過程。四面固支加筋壁板結構的幾種振動主動控制實驗說明，采用本文提出的主動控制方法，不僅在二階共振頻率外界激勵下具有優良的振動抑制效果，而且能很好的抑制不確定因素引起的整個結構的波動，使得整個閉環結構具有優良的穩態和動態性能。

［1］孫朝暉，戴 揚，孫進才.動力吸振器用于飛機壁板減振降噪的研究［J］.航空學報，1993，14(10):506－509.

［2］張志誼，王俊芳，諶 勇，等.主動隔振與聲輻射控制中的飽和抑制［J］.振動與沖擊，2009，28(5):27－32.

［3］Schiller N H，Cabell R H，Fuller C R.Decentralized control of sound radiation using iterative loop recovery［J］.Journal of the Acoustical Society of ASME ，2010，128(4):1729－1737.

［4］Poulin K C，Vaicaitis R.Vibrations of stiffened composite panels with smart materials［J］.Journal of Vibration and Acoustics－ transactions of the ASME，2004，126(3):370－379.

［5］Mukherjee A，Joshi S P，Ganguli A.Active vibration control of piezolaminated stiffened plates［J］.Composite Structures，2002，55:435 －443.

［6］Balamurugan V，Narayanan S.Finite element modeling of stiffened piezolaminated plates and shells with piezoelectric layers for active vibration control［J］.Smart Materials and Structures，2010，19:1 －21.

［7］Ren X M， LewisF L， ZhangJL.Neuralnetwork compensation control for mechanical systems with disturbances［J］.Automatica，2009，45(3):1221 －1226.

［8］Qiu Z C，Han J D，Zhang X M，et al.Active vibration control of a flexible beam using a non-collocated acceleration sensor and piezoelectric patch actuator［J］.Journal of Sound and Vibration，2009，326(3 －5):438 －455.

［9］Sharma M，Singh S P，Sachdeva B L.Modal control of aplate using a fuzzy logic controller［J］.Smart Materials ＆Structures，2007，16(5):1331 －1341.

［10］韓京清.自抗擾控制器及其應用［J］.控制與決策，1998，13(3):19－23.

［11］Han J Q.From PID to active disturbance rejection control［J］.IEEE transaction on Industrial Electronics，2009，56(3):900－906.

［12］Zheng Q，Dong L L，Gao Z Q，et al.Active disturbance rejection control for MEMS gyroscopes［J］.IEEE transaction on Control Systems Technology，2009，17(6):1432－1438.

［13］Zhao S，Gao Z Q.An active disturbance rejection based approach to vibration suppression in two－inertia systems［C］//Proceedings of the American control conference，Baltimore，2010:1520－1525.

［14］Gao Z Q.Scaling and bandwidth parameterization based controller tuning［C］//Proceedings of the American Control Conference，Denver，2003:4989 －4996.

［15］Gao Z Q.Active disturbance rejection control:a paradigm shift in feedback control system design［C］//Proceedings of the American Control Conference，Minneapolis，2006:2399－2405.

［16］Huang Y，Xue W C，Yang X X.Active disturbance rejection control:Methodology，theoretical analysis and applications［C］//Proceedings of the 29th Chinese control conference，Beijing，2010:6083 －6090.

［17］Ji H L，Qiu J H，Zhu K J，et al.Two-mode vibration control of a beam using nonlinear synchronized switching damping based on the maximization of converted energy［J］.Journal of Sound and Vibration，2010，329(3－5):2751－2767.

［18］Harari S，Richard C，Gaudiller L.New semi-active multimodal vibration control using piezoceramic components［J］.Journal of Intelligent Material Systems and Structures，2009，20(13):1603－1613.