考慮楊氏模量隨軸向溫度分布變化的轉子有限元建模方法研究

何 鵬，劉占生，劉鎮星

(哈爾濱工業大學 能源學院，哈爾濱 150001)

汽輪機和燃氣輪機在工作過程中，受到工作介質及環境的影響，轉子上存在一定的溫度分布。在溫度作用下，轉子發生熱彎曲，同時轉子材料的力學性能有所變化，影響轉子的振動特性。

在溫度作用下，轉子材料發生熱膨脹，引起轉子熱變形。轉子周向溫度分布不均勻時，將產生熱彎曲，影響轉子振動狀態。轉子的熱彎曲振動問題在工程中時常出現［1－3］。轉子熱彎曲成因可以分為周向介質及上下缸溫差［4］、動靜碰摩產生的溫差［5－8］和轉子在滑動軸承中渦動引起的Morton效應［9－10］。對于轉子熱彎曲所產生的振動問題已經有深入研究［11－12］，并且已經形成了有效的分析診斷方法和處理措施［13－15］。

溫度不僅能引發轉子熱變形，還會引起轉子材料楊氏模量的改變。不同材料的楊氏模量隨溫度變化規律不同，文獻［16］通過測量不同溫度下振動頻率的變化，得到了含鎳鋼材的楊氏模量隨溫度變化曲線。文獻［17］基于固體力學理論，推導了常用合金材料楊氏模量隨溫度的變化規律。由溫度引起材料楊氏模量的變化對轉子振動特性也有影響。晏水平等［18］引入剪切模量隨溫度的變化規律，分析了軸向溫度分布對汽輪機轉子軸系扭轉振動的影響。朱向哲等［19－20］通過引入熱應力效應，考慮溫度作用下轉子熱變形引起剛度矩陣變化，分析了溫度分布對轉子振動特性的影響。劉少權等［21］引入楊氏模量隨溫度的變化，采用有限元軟件分析了溫度場對燃氣輪機拉桿轉子臨界轉速的影響。雖然對于溫度導致材料楊氏模量變化引起的振動問題已經進行了一些研究，目前尚未有考慮溫度引起楊氏模量變化的轉子有限元模型，以分析在不同軸向溫度分布下轉子振動特性。

傳統的轉子動力學有限元模型［22］無法考慮轉子軸向溫度分布的影響，本文主要研究考慮軸向溫度分布的有限元建模。首先擬合了楊氏模量隨溫度的變化關系，結合有限元方法，推導了考慮單元內溫度分布的有限元剛度矩陣，建立了溫度分布對轉子振動特性的影響模型。通過數值仿真分析了在溫度均勻分布、軸向線性分布和軸向二次分布情況下轉子振動特性的變化。

1 楊氏模量隨溫度的變化規律

材料的楊氏模量是材料原子間作用力的體現，反映了材料應力與應變的比例關系，是材料重要的力學性能參數。對于某一材料，楊氏模量只與材料的溫度有關。

不同材料的楊氏模量隨溫度的變化規律不同。文獻［18］中，轉子材料剪切模量隨溫度變化規律為G=G0(1－c(t－t0)/100)，其中 c為常數。在文獻［19－20］中，楊氏模量隨溫度的變化規律為E(t)=207.8－0.069t－3.8 ×10－5t2。在文獻［21］中，給出了所計算壓氣機和渦輪轉子材料在不同溫度下的楊氏模量值。通過曲線擬合，可以得到文獻［21］中壓氣機轉子材料楊氏模量隨溫度的變化規律為E(t)=E0(－3.862×10－7t2－1.199 ×10－4t+1.002)，其中擬合的均方根誤差為0.001923;渦輪轉子材料楊氏模量隨溫度變化規律為E(t)=E0(－5.213×10－7t2－8.347×10－5t+1.002)，其中擬合的均方根誤差為0.003989。在文獻［16］中，作者通過測量不同溫度下叉狀物的振動頻率，得到了不同溫度下含鎳鋼材楊氏模量隨溫度的變化曲線。通過曲線擬合，可得該材料楊氏模量隨溫度變化規律為:

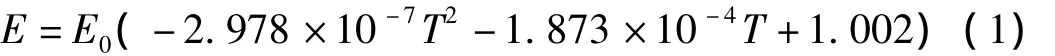
可以看出，不同材料楊氏模量隨溫度的變化規律略有不同，但大多轉子材料的楊氏模量隨溫度的變化規律可以用二次多項式形式表示:

其中，對于確定的材料，γ，β和α為常數。

2 考慮楊氏模量變化的轉子模型

根據楊氏模量隨溫度的變化規律，結合轉子軸向溫度分布，可以建立轉子有限元單元內楊氏模量的變化趨勢，得到考慮軸向溫度分布的單元剛度矩陣及轉子有限元模型。

2.1 單元內楊氏模量的變化規律

本文主要考慮轉子軸向溫度分布引起楊氏模量的變化對轉子振動特性的影響，故假設轉子各個截面溫度分布均勻，并且不考慮溫度分布引起的轉子的熱變形。

轉子有限元單元如圖1所示。假設單元內溫度軸向線性分布，兩節點溫度分別為Ti和Ti+1，則單元內任意位置處溫度可以表示為:

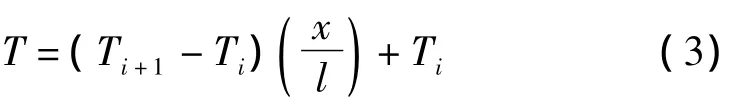
需要說明這里可以根據實際轉子軸向溫度分布情況，假設單元內溫度具有高階多項式分布形式。

結合材料楊氏模量隨溫度的變化規律，將式(3)代入式(1)中，可以得到單元內楊氏模量的軸向變化規律:

其中f(x)與單元溫度分布及軸向坐標有關:

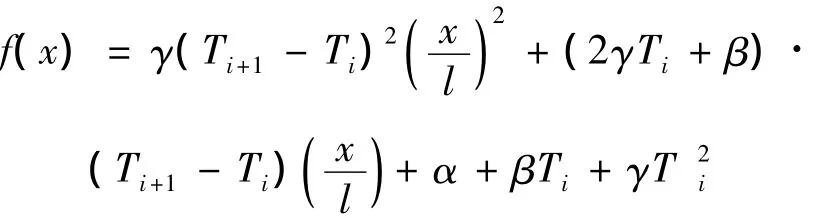
2.2 考慮溫度分布單元剛度矩陣

對于如圖1所示轉子有限元單元，假設軸向方向為z軸，則節點i和節點i+1各具有四個自由度［22］，即{x，y，－ θx，θy}T。在 XOZ 平面內，單元的自由度為{xi，θyi，xi+1，θyi+1}T。單元剛度矩陣為［22］:

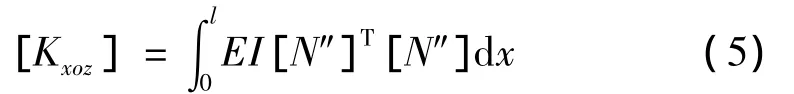
其中，E為材料楊氏模量，I為單元截面慣性矩，N為單元型函數。

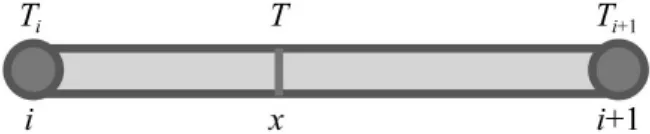
圖1 考慮溫度分布的單元模型Fig.1 Element with temperature

結合單元內楊氏模量隨溫度分布的變化規律，將式(4)代入式(5)，可以得到考慮楊氏模量隨溫度變化的單元剛度矩陣:

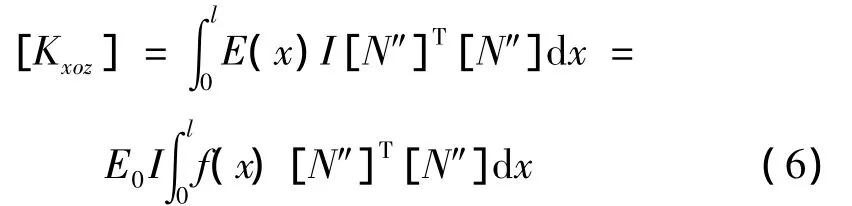
根據f(x)的表達式，可以統一寫為如下形式:

其中，ci與單元節點溫度和單元內的溫度分布相關;n與單元內溫度分布形式及楊氏模量隨溫度變化規律相關。根據楊氏模量隨溫度二次變化規律和單元內溫度線性分布的假設，這里n最大取2。

將式(7)代入式(6)中，可得考慮溫度分布的轉子單元的剛度矩陣:

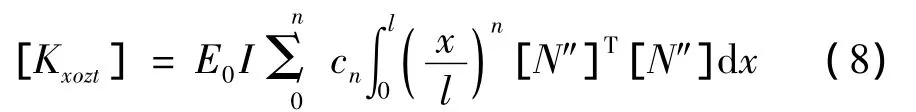
各元素的通用表達式為:

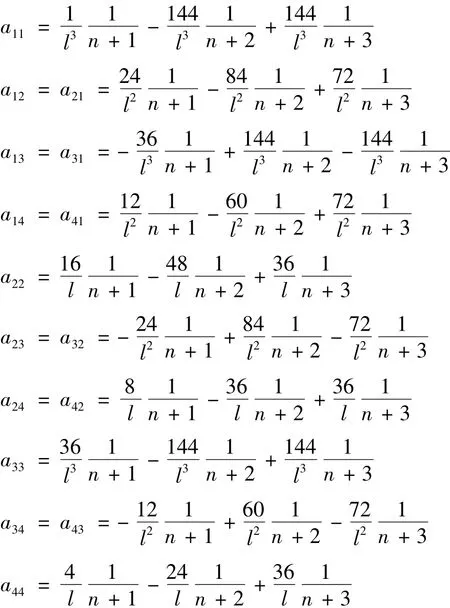
一般轉子橫向剛度相等，在YOZ平面內，單元的剛度矩陣與XOZ平面一致。綜合兩個平面內的振動，轉子單元的橫向振動自由度為{xi，yi，－ θxi，θyi，xi+1，yi+1，－ θxi+1，θyi+1}T，單元的剛度矩陣為:

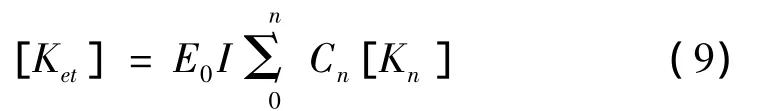
其中:

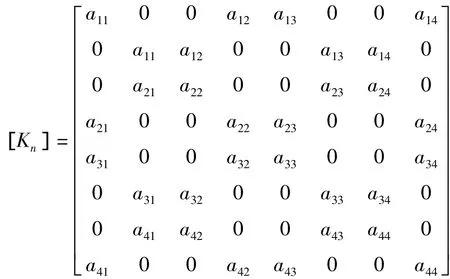
由于本文只考慮楊氏模量隨溫度變化對剛度矩陣的影響，不考慮單元的質量矩陣、陀螺力矩矩陣受溫度的影響，可采用常規方法得到［22］。

2.3 考慮楊氏模量隨溫度變化的轉子動力學方程

根據單元的質量矩陣、剛度矩陣和陀螺力矩矩陣，可以合并形成轉子系統的質量矩陣、剛度矩陣和陀螺力矩矩陣，進而可得轉子系統的動力學方程:

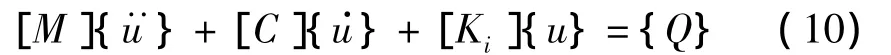
其中［M］為轉子系統的質量矩陣，［C］為包括陀螺力矩的轉子阻尼矩陣，［Ki］為考慮轉子系統溫度分布的剛度矩陣，{Q}為轉子節點載荷向量，{u}為轉子節點自由度向量。

3 結果分析

為了體現轉子軸向溫度分布對轉子振動特性的影響和便于驗證模型，下面采用簡單轉子模型，分析軸向溫度均勻分布、線性分布和二次分布情況下轉子的振動特性。轉子的結構如圖2所示，轉子長0.5 m，軸頸0.04 m，兩端剛性支承。轉子材料密度為7.85×103kg/m3，常溫下楊氏模量為205 GPa，楊氏模量隨溫度的變化規律采用式(1)函數表示。

圖2 模型轉子結構Fig.2 The structure of the rotor model

3.1 軸向溫度均布轉子振動特性變化

假設轉子溫度均勻分布，可以采用本模型分別計算不同溫度下轉子的臨界轉速。針對結構簡單，剛性支承轉子，臨界轉速可以采用如下解析式計算［23］:

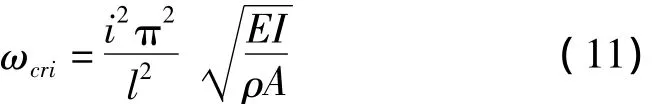
其中:i為臨界轉速階數。

從表達式可以看出，解析式將轉子當作簡支梁處理，沒有考慮轉子陀螺力矩的影響。為了便于對比分析，在計算溫度均布轉子臨界轉速時，也不考慮陀螺力矩影響，結果如表1所示。

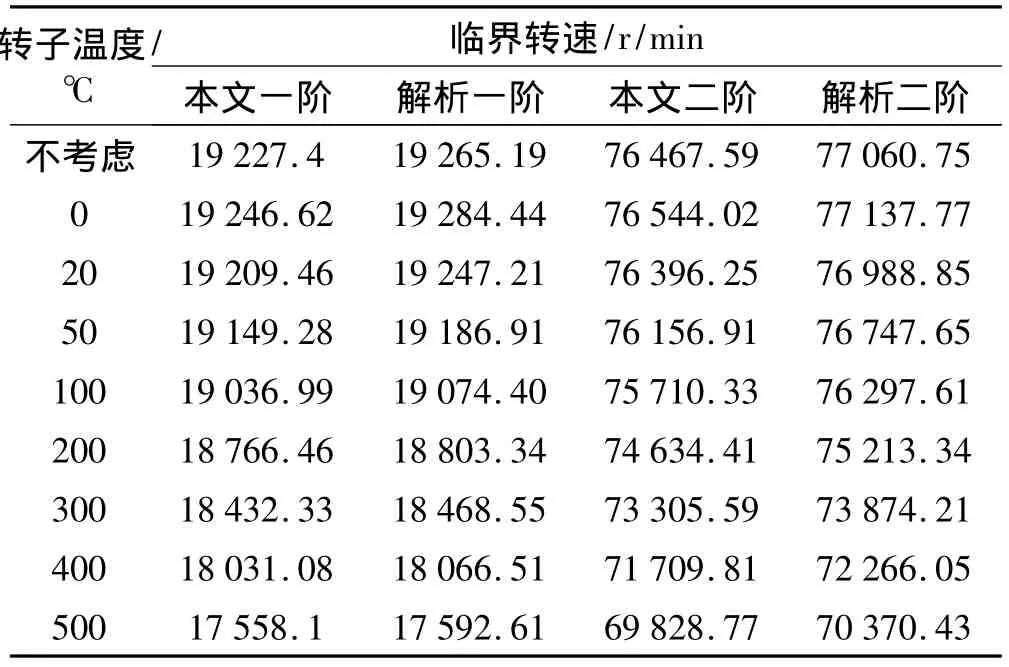
表1 模型轉子前兩階臨界轉速隨溫度變化Tab.1 Variation of model rotor critical speeds with temperature

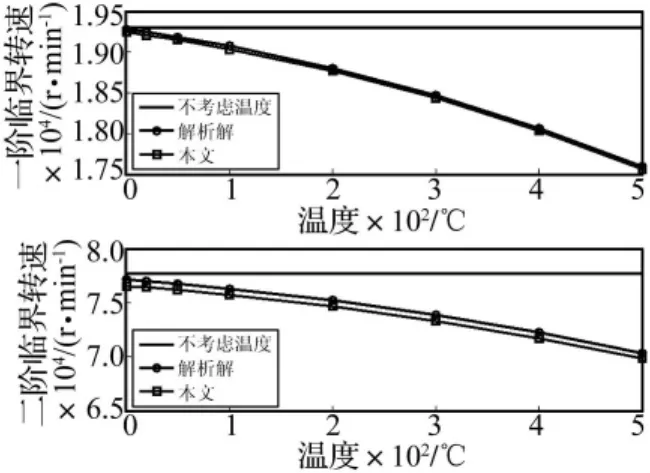
圖3 模型轉子前兩階臨界轉速隨溫度的變化趨勢Fig.3 Variation of critical speeds with the rotor temperature

轉子臨界轉速隨溫度的變化趨勢及與解析解的對比也可以從圖3看出。

從表1和圖3看出，隨著溫度的增加，轉子材料楊氏模量減小，轉子臨界轉速降低，本文模型計算結果和解析解比較接近。轉子在500℃時，轉子材料楊氏模量變為常溫值的83.39%，本文模型和解析解的前兩階臨界轉速均降低8.68%，這驗證了本文模型的正確性。

3.2 軸向溫度線性分布轉子振動特性變化

假設轉子溫度沿著軸向線性增加，其中低溫端固定為20℃，分別分析模型轉子在不同軸向溫差下的臨界轉速，結果見表2。

在軸向溫差作用下，轉子臨界轉速的變化規律如圖4所示。從圖中可以看出，隨著軸向溫差的增加，轉子的兩階臨界轉速是以拋物線規律降低。在轉子軸向溫差為500℃時，轉子一階臨界轉速降低了3.41%，二階臨界轉速降低了3.57%。

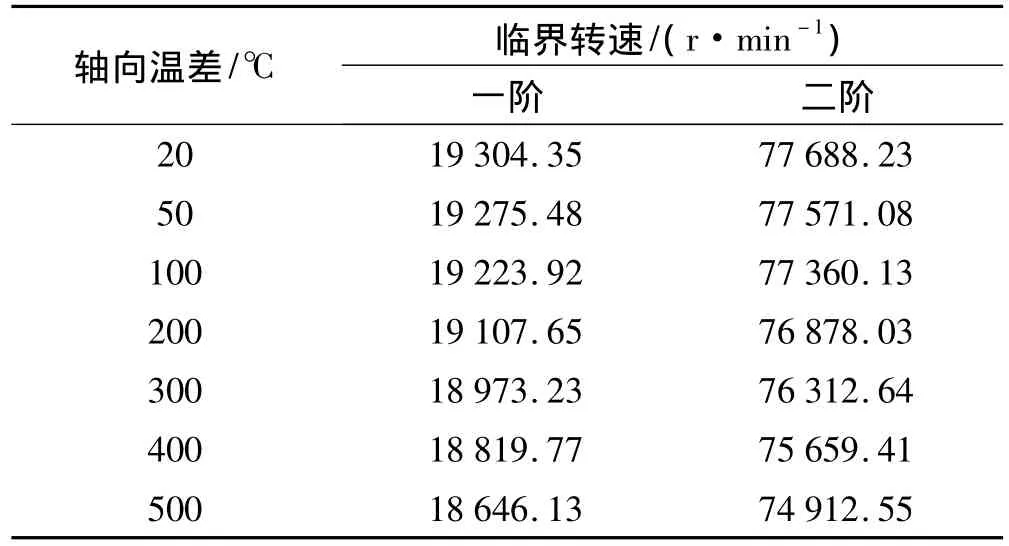
表2 模型轉子前兩階臨界轉速隨軸向溫差變化Tab.2 Variation of model rotor critical speeds with axial temperature difference

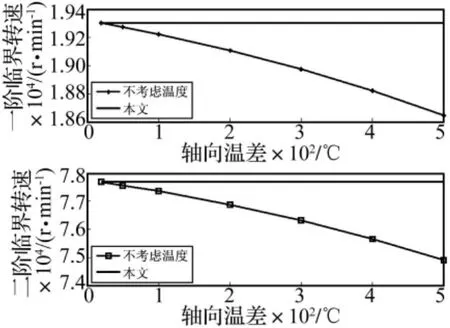
圖4 轉子前兩階臨界轉速隨線性分布軸向溫差變化趨勢Fig.4 Variation of the first two critical speeds with axial temperature difference of linear distribution

在軸向溫差作用下，轉子在高溫部位的剛度降低較多，低溫部位的剛度相對較大，這可能會使得轉子的振型發生變化。為此，對比分析了轉子在不考慮溫度分布和軸向溫差為500℃的線性分布兩種情況下轉子前兩階振型，結果如圖5所示。從圖中可以看出，在軸向溫差500℃的線性溫度分布下，轉子的振型與不考慮溫度情況之間的差別很小，故可以不考慮軸向溫度分布對轉子振型的影響。

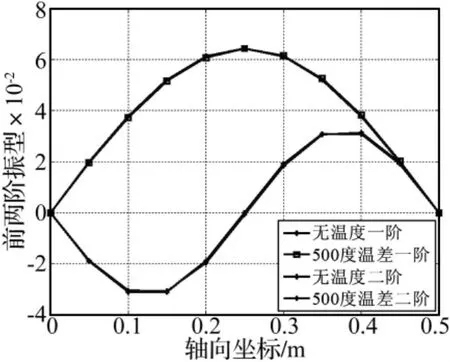
圖5 轉子前兩階振型的變化Fig.5 Variation of the first two modal shape

3.3 軸向溫度二次多項式分布轉子振動特性變化

假設轉子的溫度在軸向以二次多項式分布，如圖6所示為不同的二次多項式溫度分布，采用有限元方法分別計算各種二次多項式溫度分布下轉子的臨界轉速。

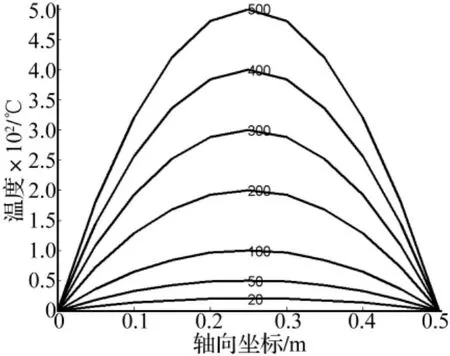
圖6 不同溫差的轉子溫度軸向二次分布Fig.6 Several temperature difference quadratic distribution of rotor axial temperature

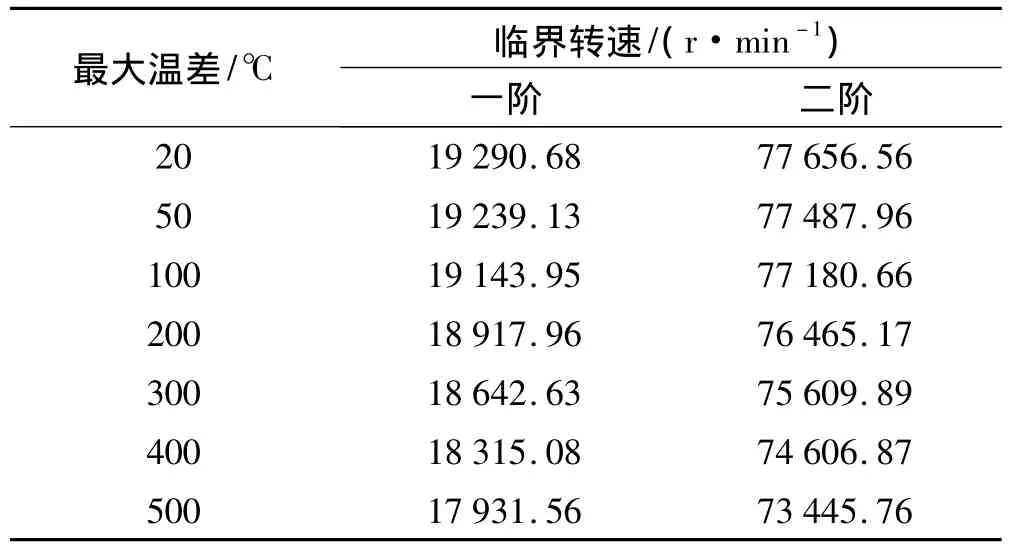
表3 不同溫差二次分布下轉子臨界轉速Tab.3 Rotor critical speeds under several temperature difference quadratic distribution of axial temperature

轉子軸向溫度在不同二次多項式分布下的前兩階臨界轉速如表3所示，臨界轉速的變化趨勢如圖7所示。轉子在軸向溫度二次分布下，臨界轉速變化比線性分布大。在最大溫差為500℃時，轉子的一階臨界轉速降低了7.11%，二階臨界轉速降低了5.46%。可見轉子軸向溫度分布不同，對轉子臨界轉速的影響差別較大。

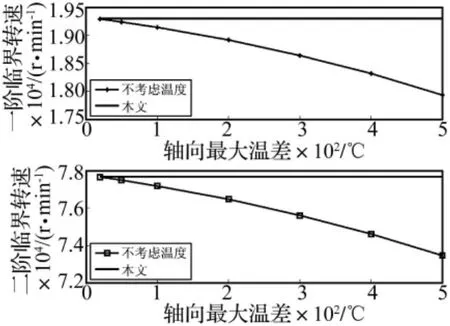
圖7 不同二次多項式溫度分布下轉子臨界轉速變化趨勢Fig.7 Variation of first two critical speeds under different axial temperature quadratic distribution

從上面三種不同形式軸向溫度分布情況下轉子臨界轉速的變化可以看出，本文的模型能夠充分考慮轉子軸向溫度分布的不同，體現轉子軸向溫度分布對轉子材料楊氏模量的影響，為轉子熱彈耦合動力學分析奠定了基礎，可以提高轉子在實際工作中臨界轉速的計算精度。

需要說明的是，本文仿真中所采用的轉子軸向溫度分布都是理想化的，實際機組中轉子軸向溫度分布是十分復雜的。例如汽輪機在工作過程中，轉子的軸向溫度變化規律在各級之間是不同的，同時軸向溫度分布也受到汽輪機啟動過程的影響。為此，在應用本文模型計算實際轉子臨界轉速時，需要首先確定轉子的溫度分布，得到轉子有限元模型各節點溫度。此外，本模型基于轉子材料楊氏模量隨溫度的變化規律，在計算中需針對不同材料，采用不同的變化規律。

4 結論

結合轉子材料楊氏模量隨溫度的變化規律，推導了考慮轉子溫度分布的單元剛度矩陣，建立了考慮轉子軸向溫度分布的有限元模型。仿真分析了模型轉子在軸向溫度均布、線性分布和二次多項式分布下，轉子臨界轉速的變化趨勢，結果表明模型能夠較好考慮轉子軸向溫度分布對轉子臨界轉速的影響，提高高溫工作轉子臨界轉速計算精度。

［1］陸 山，趙 明，任平珍，等.某型發動機轉子熱彎曲變形及其影響數值分析［J］.航空動力學報，1997，12(3):243－246.LU Shan，ZHAO Ming，REN Ping-zhen，et al.A numerical analysis of thermal bending deformation and its influence on rotor［J］.Journal of Aerospace Power，1997，12(3):243 －246.

［2］莊景菁.轉子熱彎曲引起汽輪機振動的分析和處理［J］.華東電力，2002，30(7):61－64.ZHUANG Jing-qing.Analysisand treatmentofturbine vibration caused by thermal bending of rotor［J］.East China Electric Power，2002，30(7):61 －64.

［3］吳子斌.汽輪發電機轉子突發性振動原因［J］.東北電力技術，2003，24(1):28－29.WU Zi-bin，The cause of burst vibration of the rotor of turbogenerator［J］.Northeastern Electric Power Technology，2003，24(1):28 －29.

［4］戚先萍，胡璧剛，許都純，等.轉子熱彎曲瞬態溫度場及熱彎曲變形試驗與分析［J］.燃氣渦輪試驗與研究，1997，10(2):32 －36.QI Xian-ping，HU Bi-gang，XU Du-chun，et al.Experiment and analysis of the transient temperature distribution and the thermal bending of rotor［J］.Gas Turbine Experiment and Research，1997，10(2):32 －36.

［5］Goldman P，Muszynska A，Bently D E.Thermal bending of the rotor due to rotor-to-stator rub［J］.International Journal，2000，6(2):91 －100.

［6］黃葆華，楊建剛.摩擦熱彎曲對轉子穩定性的影響［J］.振動工程學報，2001，14(1):23－28.HUANG Bao-hua，YANG Jian-gang.Influence of thermal bow of the stability of rubbing bearing-rotor system［J］.Journal of Vibration Engineering，2001，14(1):23－28.

［7］田永偉，楊建剛.基于特征值分析的摩擦轉子熱穩定性研究［J］.振動與沖擊，2010，29(7):66－68.TIAN Yong-wei，YANG Jian-gang.Thermal stability of a rubbing rotor based on eigenvalue analysis［J］.Journal of Vibration and Shock，2010，29(7):66 －68.

［8］賀 威，袁惠群，朱向哲.瞬態傳遞矩陣法分析熱彎轉子系統的熱碰摩故障［J］.東北大學學報(自然科學版)，2009(6):861－864.HE Wei， YUAN Hui-qun， ZHU Xiang-zhe. Transient transfer matrix method for thermal rub-impact faults in hot bending rotor system［J］.Journal of Northeastern University(Natural Science)，2009(6):861－864.

［9］Keogh P S，Morton P G.Journal bearing differential heating evaluation with influence on rotor dynamic behaviour［J］.Proceedings oftheRoyalSocietyofLondon.SeriesA:Mathematical and Physical Sciences，1993，441(1913):527－548.

［10］Keogh P S，Morton P G.The dynamic nature of rotor thermal bending due to unsteady lubricant shearing within a bearing［J］.Proceedings of the Royal Society of London.Series A:Mathematical and Physical Sciences，1994，445(1924):273.

［11］任平珍，柴衛東，胡壁剛，等.航空發動機轉子熱彎曲穩態響應計算方法研究［J］.燃氣渦輪試驗與研究，1996(3):27－32.REN Ping-zhen， CHAI Wei-dong， HU Bi-gang， et al.Research on the computation method of the steady state response of the thermal bending aeroengine rotor［J］.Gas Turbine Experiment and Research，1996(3):27－32.

［12］任平珍，陸 山，趙 明.轉子熱彎曲變形及其影響的數值分析方法［J］.機械科學與技術，1997，16(2):279－282.REN Ping-zhen，LU Shan，ZHAO Ming.Numerical analysis method of thermal deflection and its affection on vibration response of rotor［J］.Mechanical Science and Technology，1997，16(2):279 －282.

［13］陸 山，杜生廣，趙 明，等.降低航空發動機轉子熱彎曲及其影響方法研究［J］.航空發動機，1997(3):23－27.LU Shan，DU Sheng-guang，ZHAO Ming，et al.Research on reducing the thermal bending and its influence of aeroengine rotor［J］.Aeroengine，1997(3):23 －27.

［14］張連祥.航空發動機轉子熱彎曲引發的典型故障分析［J］.振動與沖擊(增刊)，2008，27(S):7－9.ZHANG Lian-xiang.Analysis of typical aeroengine vibration fault related to thermal bowed rotor［J］.Journal of Vibration and Shock，2008，27(S):7－9.

［15］張麗娟，楊新華，馬呈霞，等.轉子熱彎曲引起發電機組振動的診斷與處理［J］.大電機技術，2009(4):13－16.ZHANG Li-juan，YANG Xin-hua，MA Cheng-xia，et al.Remedy on vibration of turbogenerator due to thermal-caused bending of rotor［J］.Large Electric Machine and Hydraulic Turbine，2009(4):13－16.

［16］Kimball Jr A L，Lovell D E.Variation of young's modulus with temperature from vibration measurements［J］.Physical Review，1925，26(1):121 －124.

［17］潘留仙，焦善慶，杜小勇.高溫下常用合金材料線脹系數，楊氏模量與溫度的關系［J］.湖南師范大學自然科學學報，2000，23(2):47－51.PAN Liu-xian，JIAO Shan-qing，DU Xiao-yong.The relation between linear expansion coefficient and yang's modulus of alloy materials ＆ temperature at high temperature［J］.Journal of Natural Science of Hunan Normal University，2000，23(2):47 －51.

［18］晏水平，黃樹紅.汽輪發電機組轉子溫度分布對其扭轉振動的影響［J］.中國電機工程學報，2000，20(11):10－13.YAN Shui-ping，HUANG Shu-hong.Impact of temperature distribution on the torsional vibration of turbogenerator rotors［J］.Chinese Society for Electrical Engineering，2000，20(11):10－13.

［19］朱向哲，袁惠群，賀 威.穩態熱度場對轉子系統臨界轉速的影響［J］.振動與沖擊，2007，26(12):113－116.ZHU Xiang-zhe，YUAN Hui-qun，HE Wei.Effect of steady thermal field on critical speeds of a rotor system［J］.Journal of Vibration and Shock，2007，26(12):113－116.

［20］朱向哲，賀 威，袁惠群.穩態溫度場對轉子系統振動特性的影響［J］.東北大學學報:自然科學版，2008(1):113－116.ZHU Xiang-zhe，HE Wei，YUAN Hui-qun.Effects of steady temperature field on vibrational characteristics of a rotor system［J］.Journal of Northeastern University(Natrual Science)，2008(1):113－116.

［21］劉少權，張艷春，杜兆剛，等.溫度場對燃氣輪機拉桿轉子臨界轉速的影響［J］.燃氣輪機技術，2011，24(2):20－23.LIU Shao-quan，ZHANG Yan-chun，DU Zhao-gang，et al.Prediction of the influence of temperature field on the critical speeds of a rod-fastened rotor［J］.Gas Turbine Technology，2011，24(2):20 －23.

［22］鐘一諤，何衍宗，王 正，等.轉子動力學［M］.北京:清華大學出版社，1987:176－185.

［23］GentaG. Consistent matricesin rotordynamic［J］.Meccanica，1985，20(3):235 －248.