中國礦業城市空間形態特征及其空間分異

宋 飏，王士君，葉 強，王雪微

(東北師范大學城市與環境科學學院，長春 130024)

礦業城市是指因礦產資源的開發而興起或發展壯大，且在一段時期內礦業在城市產業結構中占據主導或支柱產業地位的城市，是經濟發展到一定歷史階段的產物。在世界各國為實現工業化而進行資本積累的時期，依托礦業而發展起來的礦業城市對各國經濟起到了舉足輕重的作用。礦業城市不但制約著礦業的興衰，而且在城市中占有較高比重，是我國城市的重要類型，對全國社會經濟的穩定和發展也具有重要作用。

城市空間結構和空間形態是城市地理學和城市規劃學傳統而重要的研究領域，結構的優劣影響城市功能的實現，城市空間形態作為城市空間結構的外在表象，是各種自然、社會、經濟因素綜合作用于城市的一種空間結果。而礦業城市的空間結構與形態特征的研究，以其獨特的城市化發展特征及自然條件等因素的影響成為當前學術界和實踐領域共同關注的問題［1－8］。本研究選取全國33個典型地級礦業城市作為研究對象，提取空間結構數據進行空間緊湊度和分形維數的計算與統計分析，力圖總結我國礦業城市對比其他類型城市在空間形態上的基本特征和空間分異規律，進而為礦業城市經濟轉型的空間規劃響應提供一定的理論和實踐指導意義。

1 研究樣本與數據獲取

1.1 樣本選取

根據國家發改委、中國礦業聯合會及有關學者［9］的研究結果，在全國178座礦業城市中公認的地級礦業城市有31座。本研究選取這些地級礦業城市，另外加入各項礦業指標都較高的鞍山市和松原市，共33座城市作為研究樣本(表1)。選定的33個地級礦業城市分布于中國的15個省，其中有煤礦城市21座，石油城市6座，冶金城市4座，有色金屬城市2座;發展階段處于幼年的城市3座，處于中年的23座，處于晚年的7座;無依托型礦業城市26座，有依托型礦業城市7座。無論是從城市依托礦業類型、城市發展階段，還是資源依托狀況，都基本能夠代表中國的礦業城市(圖1)。

1.2 空間數據

利用GoogleEarth截取2008年樣本城市的空間數據①GoogleEarth數據為衛星影像與航拍的整合數據，其衛星影像部分來自于美國DigitalGlobe公司的QuickBird(捷鳥)商業衛星與EarthSat公司、Sanborn公司等，2008年截取數據多為2006年前后一年的數據。，同時采用中國遙感衛星地面站RsgsMaps的數據(2006年)進行修正②中國遙感衛星地面站RsgsMaps的數據拼接圖像由Modis數據、Landsat7全國影像數據組成，是由經過二級校正的衛星數據拼接而成的，2006年在精度上地面誤差在100 m以內，圖像投影方式是等角圓錐投影。，用ArcGIS軟件對全國33個公認礦業城市的城市外圍輪廓形態進行定量分析。首先提取各城市的建設用地部分，經過一定的圖形編輯，得出2006年城市主要建成區的空間范圍示意圖，并從城市緊湊度和分形維數兩個方面探究礦業城市的空間形態特征。

2 模型與計算

2.1 緊湊度

城市外圍輪廓形態的緊湊度是反映城市空間形態的一個非常重要的指標，通常認為，緊湊城市是一種盡可能充分利用已存在的城市空間的結果，被認為是一種結束城市蔓延危害的一種方法。Thamas和Cousins認為緊湊城市具有如下優點［10］:由于城市內各部分之間聯系距離縮短，降低了人們對汽車的依賴性，減少了污染物的排放、能源的消耗;改善了公共交通的服務，總體上增加了城市交通的方便性;提高了城市基礎設施和已開發土地的利用效率，有利于解決和統籌安排各種設施。鑒于此，一些國家將“緊湊城市”策略做為城市規劃標準執行，如歐洲共同體認為“緊湊城市”是一個可持續發展的概念，指出緊湊城市可以使城市居民獲得更好的生活質量，認為緊湊城市的正面影響是廣泛的。

表1 關于中國礦業城市的代表性研究結論Tab.1 The representative conclusion of study about mining city in China

圖1 樣本礦業城市分布圖Fig.1 Distribution of the sample book of mining cities

城市形狀緊湊度的公式［11］如下，即:

式中:c指城市的緊湊度;A指城市面積;P指城市輪廓周長。c值在0～1之間，緊湊值越大，其形狀越具有緊湊性;反之，形狀的緊湊性越差。圓是一種形狀最緊湊的圖形，圓內各部分高度壓縮，其緊湊度為1;如果是狹長形狀，其值遠遠小于1。根據計算，33個樣本礦業城市的緊湊度如表2。

2.2 分形維數

城市形態分析有助于解釋地理空間復雜性的發生和演化機制。分形是研究城市形態的有效工具之一。所謂分形，是指其組成部分以某種方式與整體相似的幾何形態(shape)，或者是指在很寬的尺度范圍內，無特征尺度卻有自相似性和自放射性的一種現象［12］。研究城市分形需要計算分維，常見的城市形態分維大致可以分為3類［13］:一是邊界維數，可以采用“周長－尺度”關系和“面積－周長”關系計算;二是半徑維數，可以借助“密度－距離”關系或者“面積－半徑標度”關系計算;三是網格維數，借助“網格數目－尺度”關系計算。本研究選用邊界維數，用“面積－周長”對33個樣本城市空間形態的復雜性進行評估。

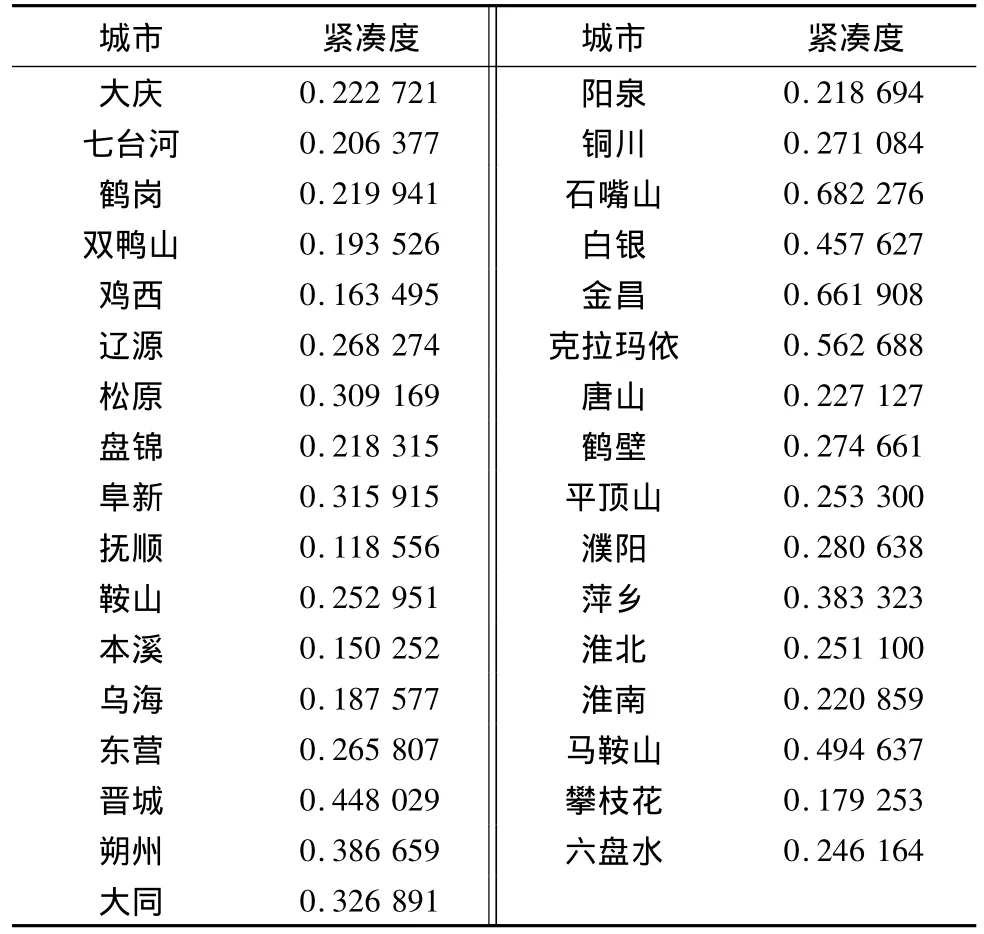
表2 樣本礦業城市空間形態的緊湊度Tab.2 The compact ratio of the sample book of mining cities

邊界維數模型最初由Batty和Longley提出，用于測算城市的邊界復雜程度，后逐漸被應用到土地利用空間結構的研究中，利用邊界維數來表達城市土地形態的復雜度。在分形維數估值中，格網法是最常見方法。使用不同大小的正方形格網覆蓋城市平面輪廓圖形，當正方形格網長度r出現變化時，覆蓋有城市輪廓邊界線的格網數目N(r)和覆蓋面積的格網數目M(r)必然會出現相應的變化。根據分形理論建立下式［14］，即:

對上式兩邊取對數，得到

式中:C為待定常數;r為度量尺度;D表示城市平面輪廓圖形的邊界維數，邊界維數D表征某一城市土地邊界的復雜曲折程度，即非線性性質的強弱。邊界維數越大，土地斑塊的數學模型非線性越強。D的理論值范圍在1.0～2.0之間。當D=1.0，表示城市形態的形狀為正方形，當D=2.0，表示城市形態的形狀最復雜;當D=1.5，表示該城市處于一種類似于布朗運動的隨機狀態。

計算邊界維數首先要利用ArcGIS對城市在不同大小正方形格網覆蓋下提取不同的點對，即N(r)和M(r)1/2，然后在SPSS中得到兩者的雙對數散點圖;最后通過最小二乘法對lnN(r)和 lnM(r)1/2進行回歸擬合，計算出33個樣本城市的邊界維數D(表3)。

表3 樣本礦業城市空間的邊界維數Tab.3 The fractal dimension of the sample book of mining cities

3 結果分析與討論

3.1 礦業城市空間形態對比特大城市的基本特征

將33個樣本礦業城市與中國31個特大城市緊湊度的數據頻率分布進行比較，得到圖2。通常認為，礦業城市空間形態的緊湊度較低，發展呈分散態。由圖2可以看出，礦業城市空間整體趨于分散，緊湊度多數在0.1～0.3之間，而全國特大城市的緊湊度多數也在0.1～0.3之間，說明中國當前的城市空間都較為分散，這與中國當前快速城市化的階段相對應，即用地擴展多軸向延伸或飛地跳躍。礦業城市緊湊度的頻率最高出現于0.25，有13個城市;而特大城市頻率分布則相對緩和，主要集中于0.15(8個城市)和0.25(8個城市)。可以認為，礦業城市空間形態緊湊度低，而特大城市空間緊湊度也相對不高，這符合國家當前城市空間擴展的態勢，即經濟快速增長階段城市空間呈分散布局。

圖2 礦業城市與特大城市的緊湊度比較［14］Fig.2 The comparison of the compact ratio between mining cities and megacities

將樣本城市與中國31個特大城市的分形維數數據進行比較，得到圖3。由圖3可以看出，礦業城市的邊界更趨于復雜，相對集中于1.45～1.55之間，最大頻率出現在1.50處，共有10個城市;而特大城市邊界維數的分布略顯均勻，集中于1.30～1.55之間，最大頻率出現在1.45處，共有11個城市。相比而言，礦業城市空間的邊界比較復雜，呈不規則狀態，這是由于礦業開采空間的復雜性決定的，其空間擴展也體現為土地的近域侵蝕或飛地跳躍，而非成塊開發。

圖3 礦業城市與特大城市的分形維數比較［14］Fig.3 The comparison of the fractal dimension between mining cities and megacities

3.2 礦業城市空間形態的空間分異

對樣本礦業城市緊湊度進行聚類，可以看出，就礦業城市內部而言，撫順的緊湊度最低，本溪、雞西、攀枝花、烏海、雙鴨山等城市由于礦業基底的控制，空間形態呈分散格局，多數典型礦業城市的緊湊度位于0.2～0.3之間，而有依托的松原、大同，以及處于開發初級階段的晉城、萍鄉、朔州、克拉瑪依、金昌、石嘴山等城市的緊湊度則相對較大，說明城市用地發展相對緊湊集約。另外，位于西部地區的城市緊湊度大，其次是中原地區，而東北地區和西北地區的礦業城市空間緊湊度最低，這主要是由于東北和西北較之其他地區的礦業城市更為典型，對礦業的依存度更大，且受地形的限制較少。

對樣本礦業城市邊界維數進行聚類，可以發現，就礦業城市內部而言，分維較大的城市主要為東北和西南的典型礦業城市，表明其城市邊界曲折、彎曲多且復雜，主要是由于這些礦業城市空間擴散更多體現為自然屬性的自組織規律。而中部地區城市的分維度次之，城市邊界相對較為規律，這與城市的空間他組織相關，空間擴展受規劃控制的痕跡明顯。相反，西北的礦業城市分維數最低，城市發展分區擴展呈規模塊狀的整體開發，這也與城市的初級發展階段和相應較小的城市人口規模相關。

3.3 緊湊度與分形維數相關分析

由礦業城市緊湊度與邊界維數的散點比較，可以發現緊湊度與邊界維數呈負相關，通過SPSS進行相關分析，緊湊度與分形維數的相關系數(r)為－0.929，說明城市空間邊界越復雜，其緊湊度越低，城市處于離散狀態;城市邊界越規整，緊湊度越高，城市空間越集中(圖4)。

圖4 礦業城市緊湊度與邊界維數的散點比較Fig.4 The scatter plot between the compact ratio and the fractal dimension of the samples of mining cities

3.4 城市空間形態與人口規模相關分析

城市發展的人口規模與城市空間形態具有一定程度的相關。由樣本城市緊湊度與城市人口的相關散點圖可以看出，城市的人口規模與緊湊度呈負相關，即礦業城市人口越多，城市規模越大，城市的緊湊度越低，人口規模大的城市相對分散(圖5)。分析邊界維數可以看出，城市邊界的復雜程度與城市人口呈正相關，即城市規模越大，邊界越復雜;城市規模越小，城市空間的發展就相對平衡(圖5)。

3.5 城市空間形態與經濟發展相關分析

經濟力量始終是城市空間結構形成與演變的根本動因，其活動的內容和方式決定了城市建設的對象和目標。從礦業城市空間形態與經濟發展的相關性可以發現，礦業城市的經濟發展水平越高，城市越趨于集中;經濟發展水平最低，城市也趨于集中;而位于經濟發展中游水平的城市，緊湊度最低，呈分散狀態(圖6)。而城市的邊界維數則沒有表現出明顯的規律，只是體現出弱相關，經濟發展水平很低的城市邊界維數偏高，說明城市初期發展時空間無序復雜;經濟發展水平在人均GDP 2 000元/人的城市邊界維數偏低，處于填充階段;隨著經濟發展水平的提高，邊界維數擴大，城市邊界擴展又趨于復雜，說明城市進入一個新的擴展期。這是一個循環反復的過程，城市空間的邊界維數呈現若干“U”形發展的集合。但是需要指出的是，這是基于33個樣本城市當時數據的分析，城市經濟發展對城市空間作用的影響還需針對一個城市的階段性發展進行研究而確定。

圖6 樣本礦業城市的緊湊度、邊界維數與人均GDP散點圖Fig.6 The scatter plot between the compact ratio and per capita GDP，and between the fractal dimension and per capita GDP of sample book of mining cities

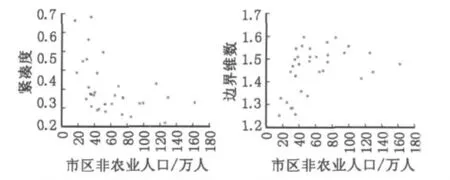
圖5 樣本礦業城市的緊湊度、邊界維數與市區非農業人口散點圖Fig.5 The scatter plot between the compact ratio and non-agricultural population and between the fractal dimension and non-agricultural population in urban areas of the sample book of mining cities

4 結論

通過對33個樣本礦業城市緊湊度和邊界維數兩個指標進行計算和相關分析，以及礦業城市空間形態與人口規模、經濟發展水平關系的討論，與全國特大城市的比較，可以初步得出如下結論:(1)礦業城市空間形態的緊湊度較低，發展呈分散態。(2)礦業城市空間的邊界比較復雜，呈不規則狀態。(3)礦業城市緊湊度與邊界維數呈負相關。(4)從空間分異而言，處于開發初期的礦業城市一般緊湊度較大，而處于開發中期的緊湊度相應減小;有依托的礦業城市緊湊度大，無依托發展起來的礦業城市緊湊度較小，空間相對分散;西部礦業城市的緊湊度大，其次是中原地區，而東北和西北的礦業城市空間緊湊度最低。(5)從分維的空間分異來看，東北和西南典型礦業城市空間維數較大，受自然屬性和礦產基底制約，城市邊界曲折、彎曲多且復雜;而中部地區城市分維數次之，受城市空間他組織和人為規劃影響，城市邊界相對較為規律;西北的礦業城市分維數最低，城市發展分區擴展呈規模塊狀的整體開發。(6)礦業城市空間形態與人口規模和社會經濟發展存在相關。

［1］焦華富，陸林.西方資源型城鎮研究的進展［J］.自然資源學報，2000，15(3):291 －296.

［2］李文彥.煤礦城市的工業發展和城市規劃問題［J］.地理學報，1978，45(3):63 －77.

［3］趙景海.我國資源型城市發展研究進展綜述［J］.城市發展研究，2006，13(3):86 －91.

［4］馬清裕.論工礦區城鎮的發展與布局［C］//中國科學院地理研究所.城鎮與工業布局的區域研究.北京:科學出版社，1986.

［5］劉云剛.中國資源型城市的發展機制及其調控對策研究［D］.長春:東北師范大學，2002.

［6］王青云.資源型城市經濟轉型研究［M］.北京:中國經濟出版社，2003:13－20.

［7］樊杰.我國煤礦城市產業結構轉換問題研究［J］.地理學報，1993，48(3):218 －225.

［8］李國平，玄兆輝.撫順主導產業演替與城市經濟發展及對其他煤炭城市的啟示［J］.地理科學，2005，25(3):281－287.

［9］劉云剛.中國資源型城市界定方法的再考察［J］.經濟地理，2006，26(6):940 －944.

［10］Gert D R.Environmental Conflicts in Compact Cities:Complesity，Decision-making and Policy Approaches［J］.Environment and Planning B:Planning and Design，2000，27(2):151 －162.

［11］Betty M.Exploring Ironist Fields:Space and Shape in Architectural and Urban Morphology［J］.Environmental and Planning B:Planning and Design，2001，28(2):123－150.

［12］徐建華.現代地理學中的數學方法［M］.第2版.北京:高等教育出版社，2002:393.

［13］陳彥光，劉繼生.城市形態分維測算和分析的若干問題［J］.人文地理，2007，22(3):98 －103.

［14］王新生，劉紀遠，莊大方，等.中國特大城市空間形態變化的時空特征［J］.地理學報，2005，60(3):392－400.