復合材料封閉變截面薄壁梁自由振動分析

馬靜敏， 任勇生，姚文莉

(1.山東科技大學 理學院，山東 266510;2.山東科技大學 機械電子工程學院，山東 266510;3.青島理工大學 理學院，青島 266510)

復合材料由于輕質、高強度、高剛度以及抗疲勞性能突出等優點［1－2］，在工程領域中得到了廣泛的應用。封閉截面復合材料薄壁梁是航空、宇航結構及風力機葉片的主要結構形式，研究其振動動態特性對其結構動力學設計具有十分重要的意義。

Mansfield等［3－5］提出復合材料封閉截面薄壁梁的運動模型，由于該模型忽略了梁的橫向剪切變形和橫截面的翹曲影響，僅適用于解決具有特定鋪層順序的復合材料梁的振動問題。Libove［6］建立了用于計算封閉截面薄壁梁剪切流和正應力的簡單理論，該理論雖然考慮了彎曲剪切變形，但是沒有考慮到由于不均勻翹曲引起的剪切變形。Librescu等［7－11］建立了廣泛適合于工程領域問題的模型，該模型引入了彎曲中的剪切彈性變形的影響，但是翹曲扭轉變形被忽略了。

上述這些研究都是針對等截面直梁的復合材料薄壁結構模型進行靜力或動力建模與分析，而實際的風力機葉片、機翼截面尺寸和形狀是變化的，所以研究變截面復合材料薄壁梁的動力學性能對于解決工程實際問題具有重要意義。Librescu 等［8，12－14］對復合材料封閉截面薄壁梁進行了一系列的研究，建立了一套理論體系，用于解決等直梁、變截面梁和變截面旋轉梁的振動問題。這些研究考慮經典的由于扭轉產生的翹曲和橫向剪切變形的影響，使用哈密頓原理獲得振動微分方程。采用這種方法由于需要涉及分部積分運算，推導過程較為繁瑣。

本文綜合考慮了均勻軸向拉伸、繞y軸和z軸的彎曲所引起的截面翹曲，但是暫時未考慮橫向剪切變形，基于拉格朗日方程推導出復合材料封閉變截面薄壁梁的自由振動方程。可以看到，相對于哈密頓原理，本文所采用的方法使公式推導變得十分簡潔。在建立復合材料封閉變截面薄壁梁振動微分方程的基礎上，通過應用迦遼金法，通過數值計算得到周向均勻剛度(CUS)和周向反對稱剛度(CAS)配置的矩形變截面薄壁懸臂梁的固有頻率，并且與ANSYS有限單元法的計算結果進行了比較。分析了復合材料的各向異性以及纖維鋪層角和截面變化對復合材料封閉變截面薄壁梁固有振動的影響。

1 自由振動方程推導

1.1 薄壁梁動能和勢能

截面形狀任意且沿軸向任意變化的細長變截面薄壁彈性梁及參考坐標系如圖1所示。其中，L表示桿件的長度，h表示截面任意位置處的壁厚，R表示截面任意位置處的中線半徑，d表示截面的特征尺寸，且滿足下列條件:

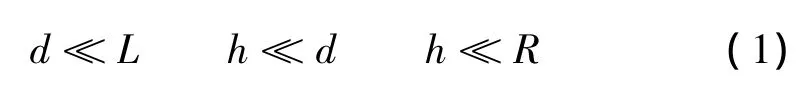
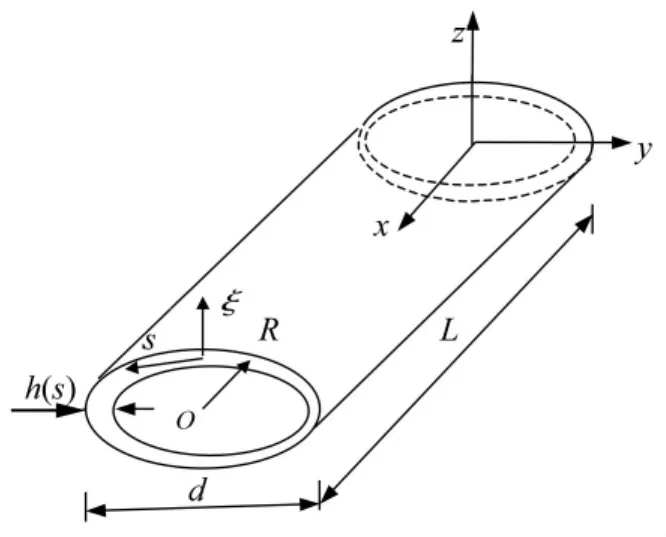
圖1 薄壁梁幾何圖及參考坐標系Fig.1 Beam geometry and coordinate systems

為了分析該梁的自由振動，定義x位置所在的截面沿x，y，z坐標軸方向的平均位移分別為 U1(x)，U2(x)，U3(x)，該截面扭轉變形的扭轉角為φ(x)。

懸臂梁上任意一點沿坐標系(x，y，z)的三個坐標軸方向的位移分量為［16］:

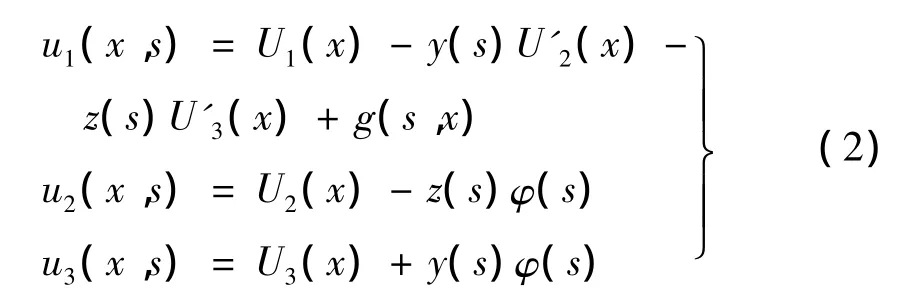
其中:g(s，x)表示由于均勻軸向拉伸、繞y軸和z軸的彎曲所引起的截面翹曲。

薄壁梁的動能和勢能為［16］:

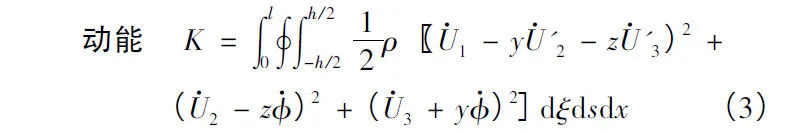
其中:(·)，(··)表示對時間t求1階和2階導數，依次類推;()'，()″表示對位置坐標x求1階和2階導數，依次類推。

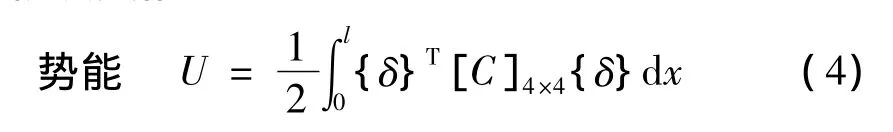
該勢能表達式是根據復合材料薄壁結構的特點，依據二維各向異性殼理論，綜合考慮了截面薄壁特點和翹曲影響建立的。此外，由文獻［16］可知，［C］4×4中的元素都是由封閉曲線積分計算得到的，因此充分反映了封閉截面的特點。

1.2 薄壁梁拉格朗日方程

對于三維連續系統 κ =κ(x，y，z，t)，相應的拉格朗日函數為 L= ∫∫∫ζd x d y d z，其中 ζ為拉格朗日密度［18］。根據薄壁梁的動能和勢能，拉格朗日密度為:

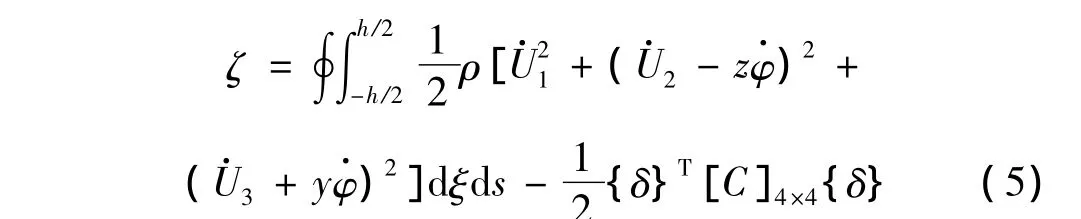
對該薄壁桿件系統應用哈密頓原理有:

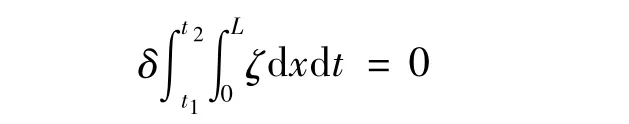
交換積分與變分符號可得:

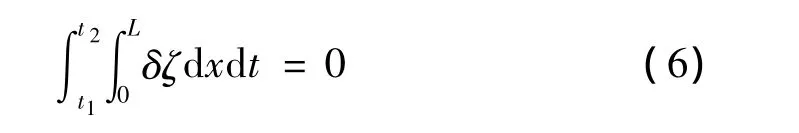
其中:

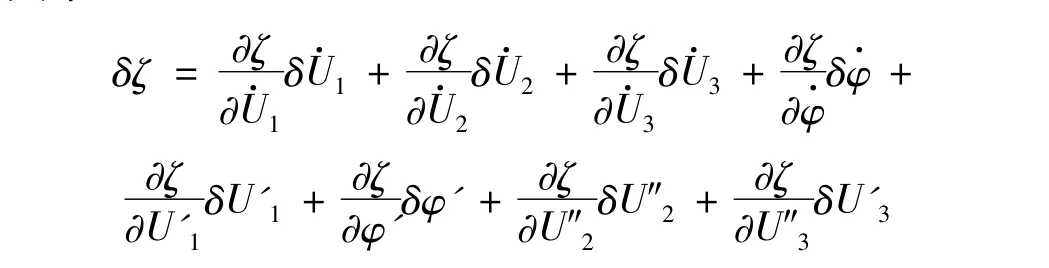
將上式適當變換，代入式(6)，并注意到:

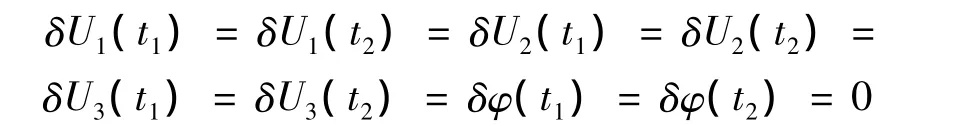
可得:

因為在(t1，t2)內:δU1，δU2，δU3，δφ 都不等于零，所以可得薄壁梁的拉格朗日方程為:

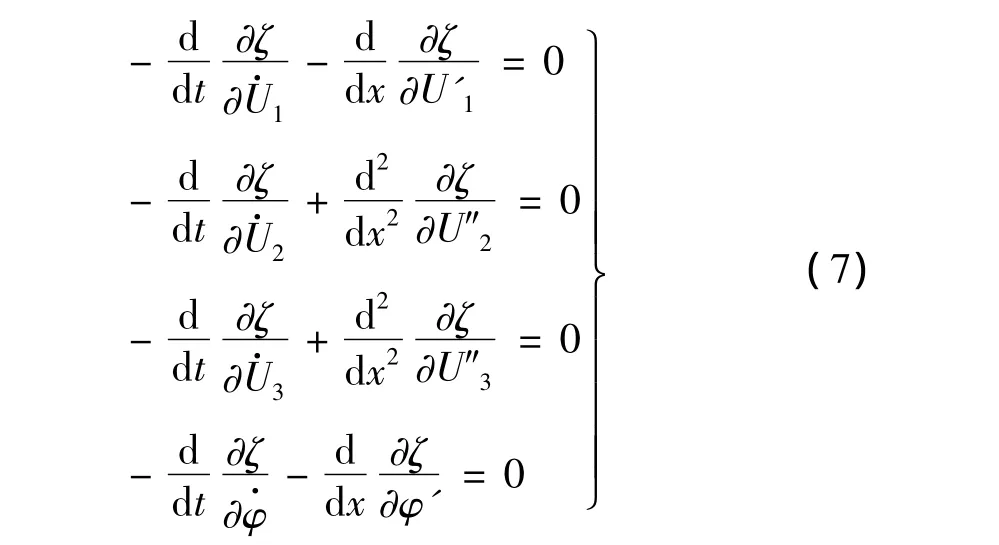
1.3 變截面薄壁梁自由運動方程

對于變截面直桿件而言，［C］4×4隨截面位置的變化而變化。將式(5)代入式(7)中，可得復合材料薄壁梁的自由運動方程為:

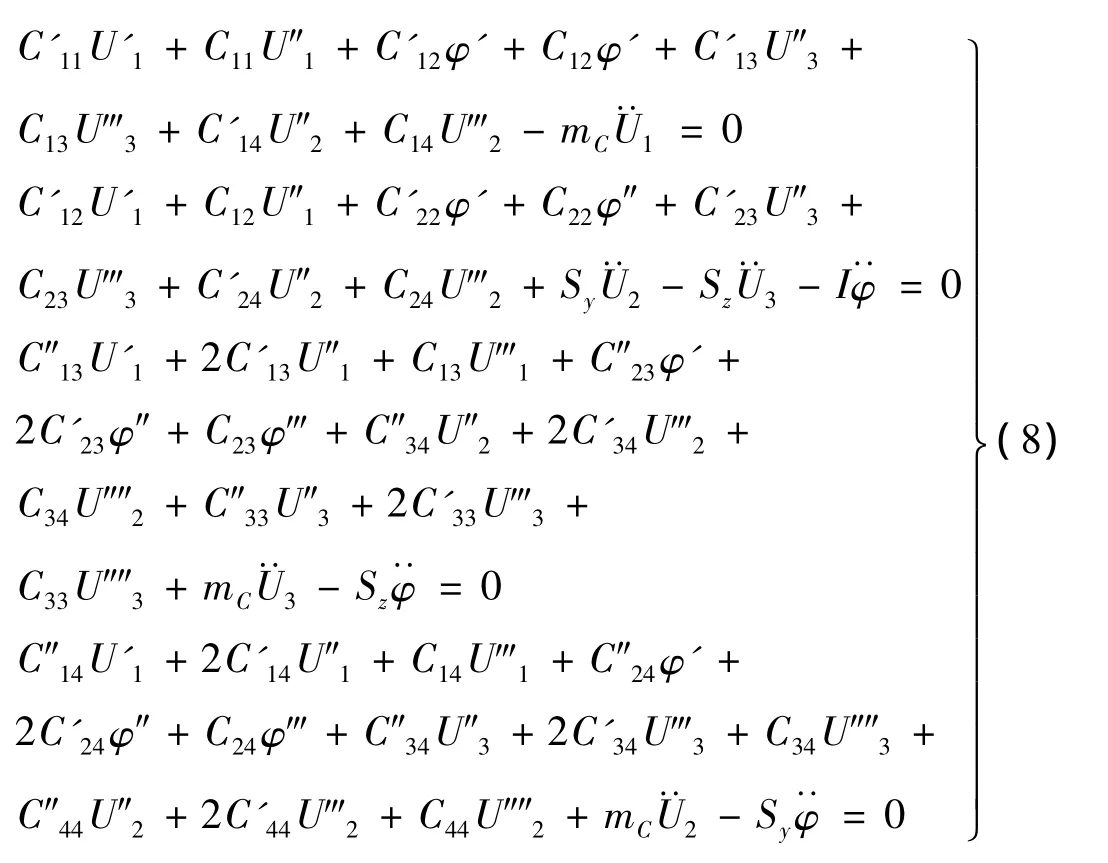
其中:

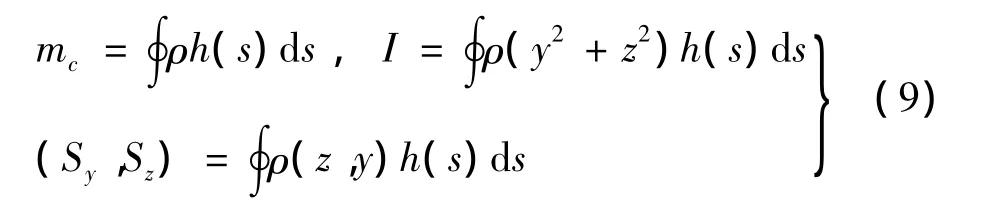
等直梁的情況下，式(8)與文獻［16］直接應用哈密頓原理建立的振動微分方程是一致的。

2 應用

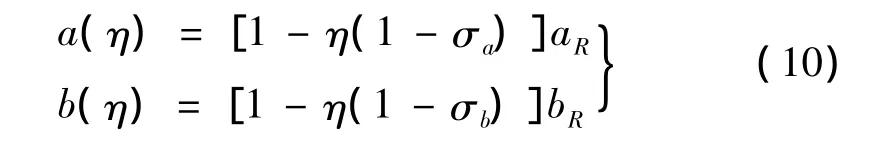
其中:σa=aT/aR，σb=bT/bR表示錐度，η=x/l表示橫截面位置的的無量綱量且η∈［0，1］。下標R和T分別表示根截面和端截面。若規定由根部到端部截面尺寸逐漸減小，則 σa∈［0，1］和 σb∈［0，1］，且錐度取0值時對應著端節面尺寸變為0，而取1時對應著截面尺寸不變化。

本文將式(8)的運動微分方程用于求解矩形變截面薄壁層壓復合材料懸臂梁的固有頻率。層壓板采用兩種鋪設方式，一種是CUS，一種是CAS。矩形截面梁的各項參數，材料的力學性能，鋪層方式見圖2、圖3和表1。矩形截面的寬度，高度隨著截面位置呈線性變化。任一位置x處的截面寬度和高度可以表示為:

表1 薄壁梁尺寸和材料性能參數Tab.1 Cantilever geometry and properties

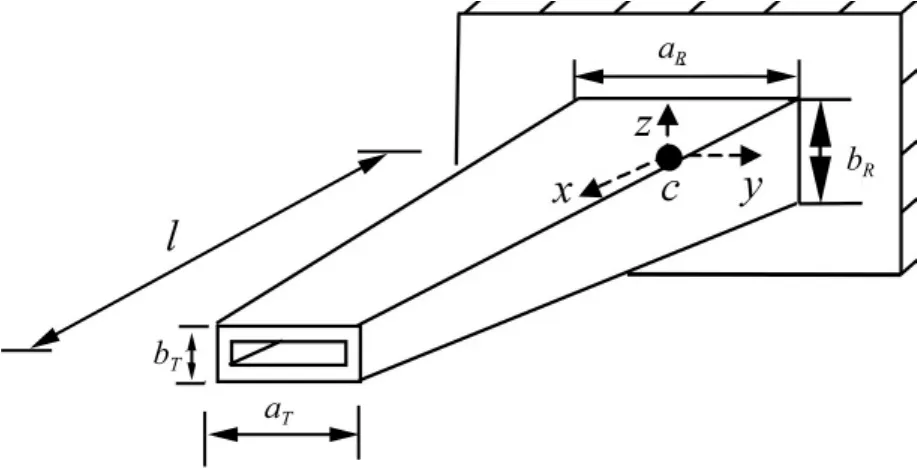
圖2 矩形梁幾何形狀參數Fig.2 The geometry of box beam

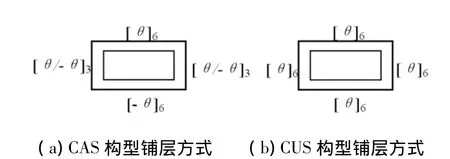
圖3 兩種鋪層方式Fig.3 Two cross-section layup

2.1 兩種構型梁的自由振動微分方程

對于CUS結構來說，由于軸向剛度、耦合剛度、剪切剛度、壁厚及材料密度在全截面上是常數 ，所以C13=C14=C23=C24=C34=0，且靜矩Sy=Sz=0。式(8)可以簡化為:

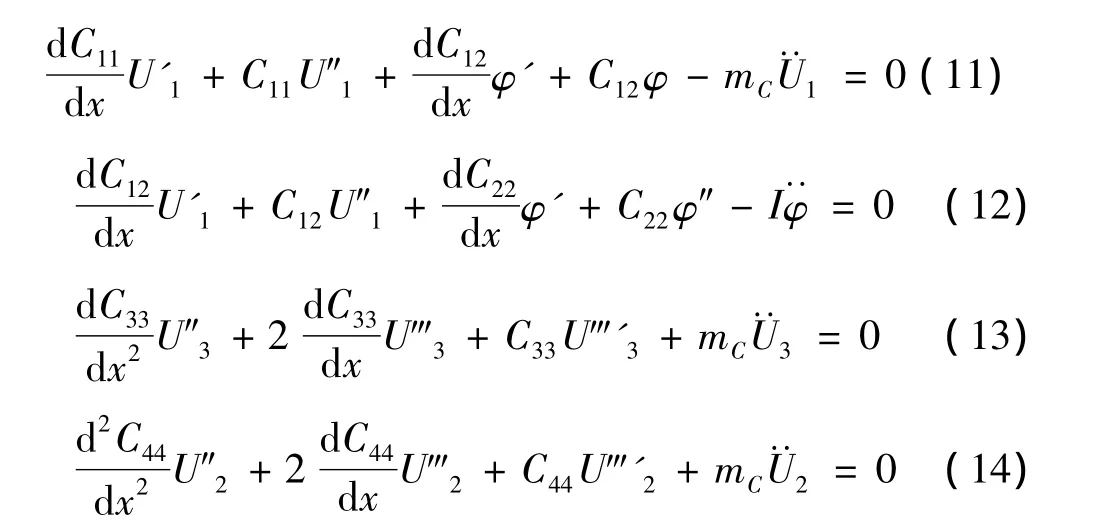
從運動方程可以得到，對于CUS構型的薄壁梁來說，式(11)和式(12)描述了拉伸與扭轉的耦合振動，式(13)描述了繞z軸的彎曲振動，式(14)描述了繞y軸的彎曲振動。

對于CAS結構來說，軸向剛度、壁厚及材料密度在全截面上是常數，而矩形截面的耦合剛度B對立邊符號相反，所以C12=C13=C14=C24=C34=0，且靜矩Sy=Sz=0。式(8)可以簡化為:

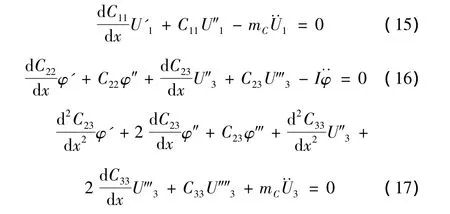
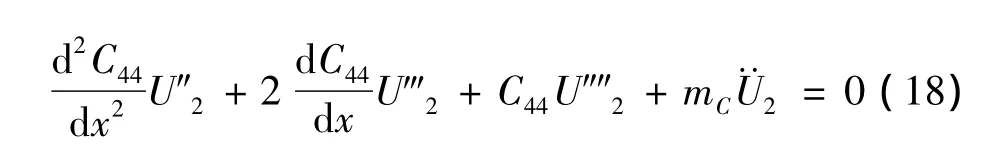
從運動方程可以得到，對于CAS構型的薄壁梁來說，式(16)和式(17)描述了繞y軸彎曲與扭轉的耦合振動，式(15)描述了軸向振動，式(18)描述了繞z軸的彎曲振動。

顯然，由于復合材料的力學性能隨著鋪層方式發生變化，不同的鋪層方式，將引起不同的耦合振動，CUS構型存在拉扭耦合振動，而CAS構型將引起彎扭耦合振動。因此可以通過對復合材料進行彈性剪裁來獲得所需要的力學性能。

2.2 固有頻率求解方法

采用連續系統振動和穩定性分析通用的Galerkin近似求解方法［19－20］，利用假設振型消除葉片空間位置變量，將自由振動方程轉化為關于時間的常微分方程。假定梁的軸向變形、扭轉變形和彎曲變形可以表示如下:

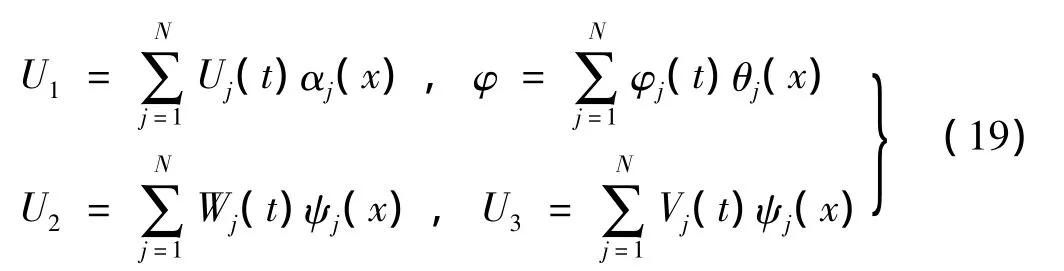
拉伸、彎曲和扭轉選取標準的非旋轉、非耦合、均勻懸臂梁的振型函數［21］:

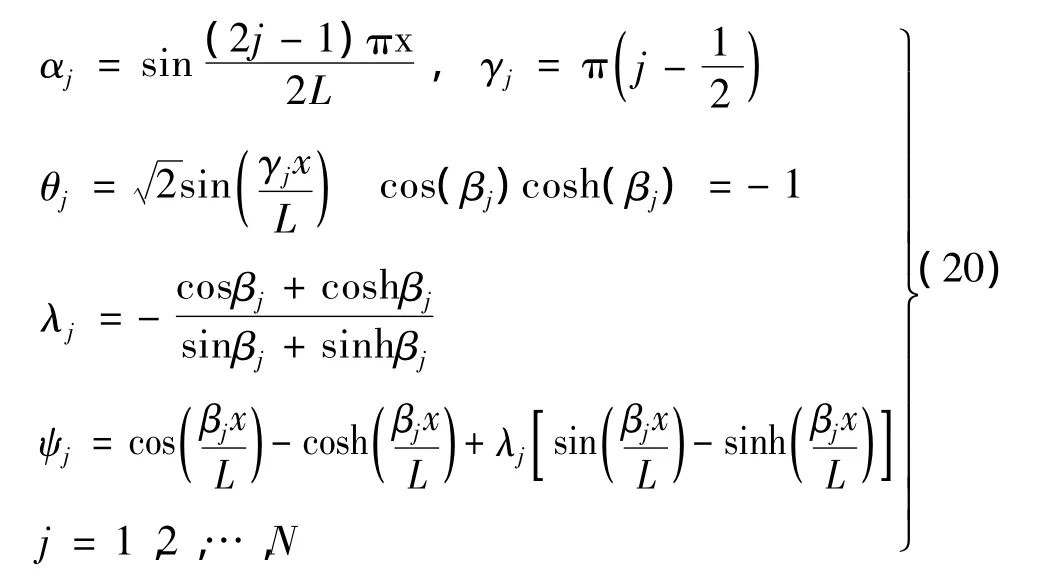
將式(19)，式(2

0)代入CUS構型梁的振動微分方程式(11)～式(14)，由Galerkin法，通過振型函數加權積分，得:

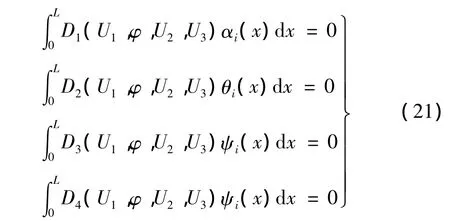
其中:D1(U1，φ，U2，U3)，D2(U1，φ，U2，U3)，D3(U1，φ，U2，U3)，D4(U1，φ，U2，U3)分別表示振動方程式(11)～式(14)等號左邊的表達式。

式(21)經化簡可得到下列的CUS構型薄壁變截面梁的4N個常微分方程組:

其中:

上述矩陣中的元素為:

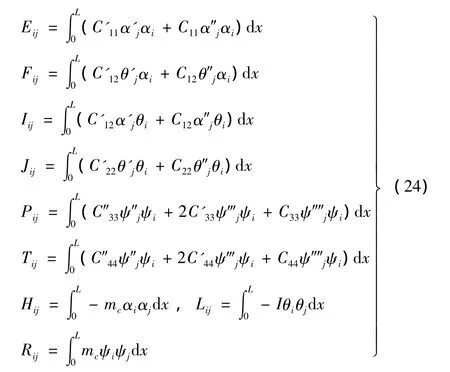
同理可得CAS構型梁的4 N個振動微分方程也為式(22)，M陣和K陣與CUS構型相同。CAS構型薄壁變截面梁的K陣為:

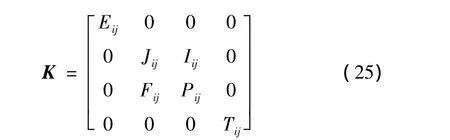
其中:

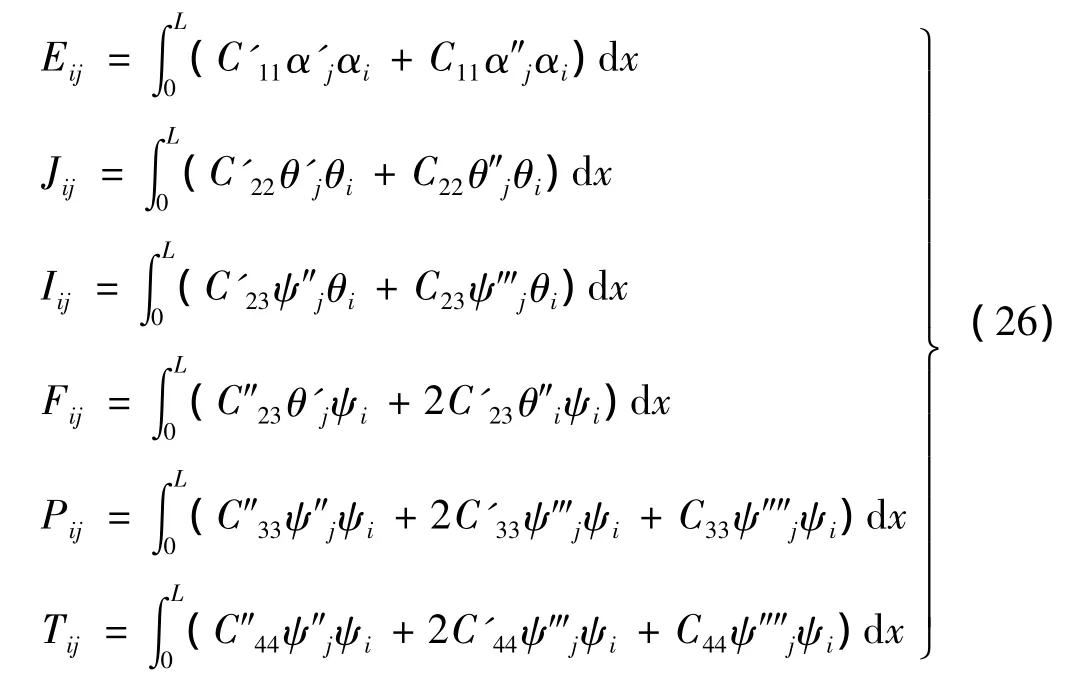
求解式(22)可得不同構型下矩形變截面薄壁梁各種振動解析解的固有頻率。

2.3 兩種構型梁振動固有頻率數值分析

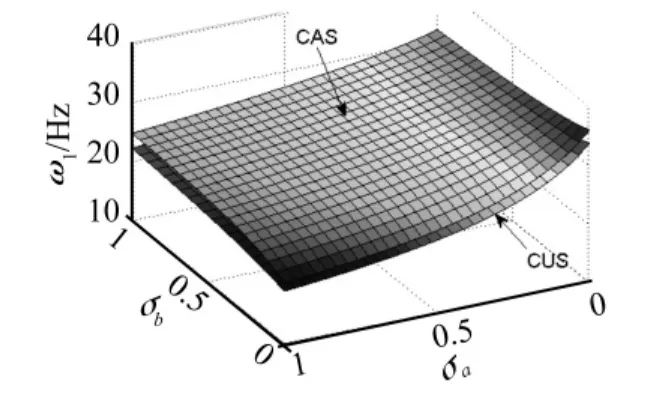
圖4 ω1隨錐度變化規律Fig.4 ω1 vs taper ratio

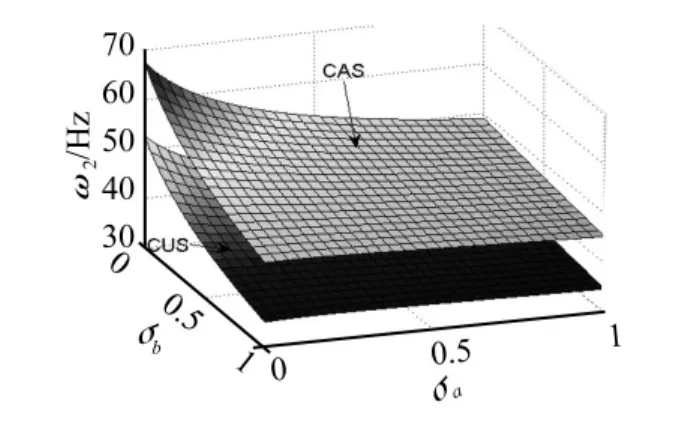
圖5 ω2隨錐度變化規律Fig.5 ω2 vs taper ratio

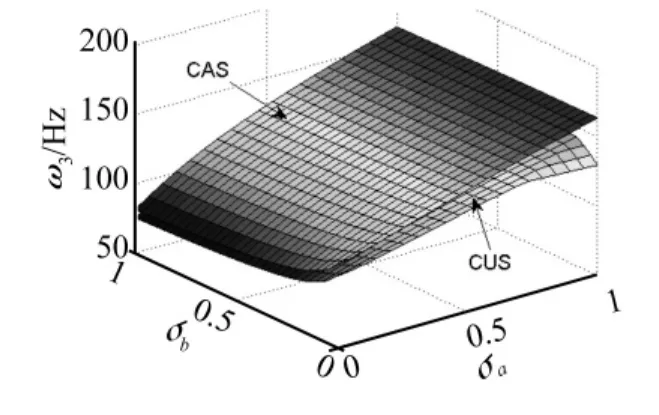
圖6 ω3隨錐度變化規律Fig.6 ω3 vs taper ratio

將CAS和CUS構型梁在30°鋪層角時前五階固有頻率隨σa和σb的變化繪制成曲面圖，如圖4～圖8所示。由圖4～圖8可知，無論錐度如何變化，CAS構型的前五階固有頻率要大于CUS構型的固有頻率且兩種構型固有頻率隨錐度的變化規律基本是一致的。

令 σb=1只有 σa變化和令 σa=1只有 σb變化，CUS構型前五階固有頻率隨σa和σb單獨變化規律如圖9和圖10所示，CAS構型如圖11和圖12所示。由圖9～圖12可以說明，梁的固有頻率隨σa的變化規律和隨σb的變化規律是不同的，而兩種構型梁隨σa的變化規律基本相同，隨σb的變化規律也基本相同。這種變化規律的差異是因為前五階振動分別屬于不同的振動模態，而錐度的變化，對于不同的振動模態的剛度影響不同。此外，圖10和圖12中的曲線存在著尖點，是因為固有頻率由小到大順序排列的緣故，并非固有頻率隨錐度不光滑地變化。

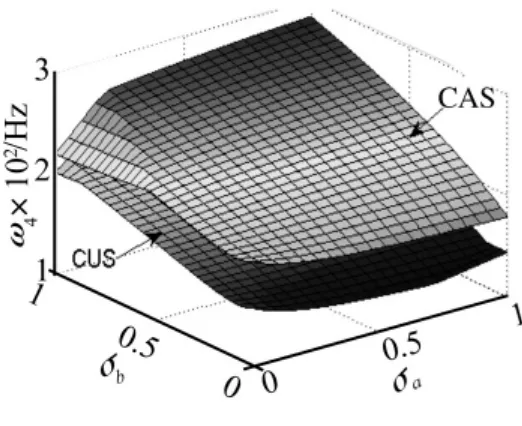
圖7 ω4隨錐度變化規律Fig.7 ω4 vs taper ratio

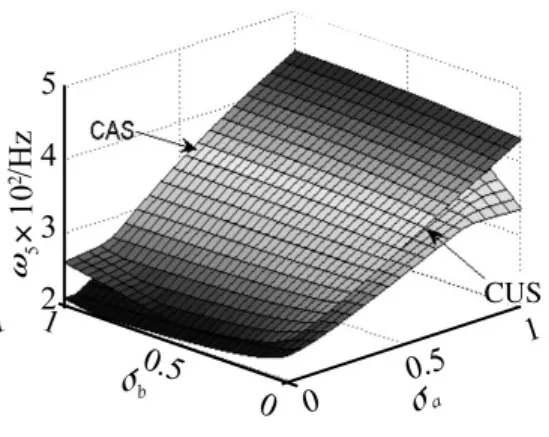
圖8 ω5隨錐度變化規律Fig.8 ω5 vs taper ratio

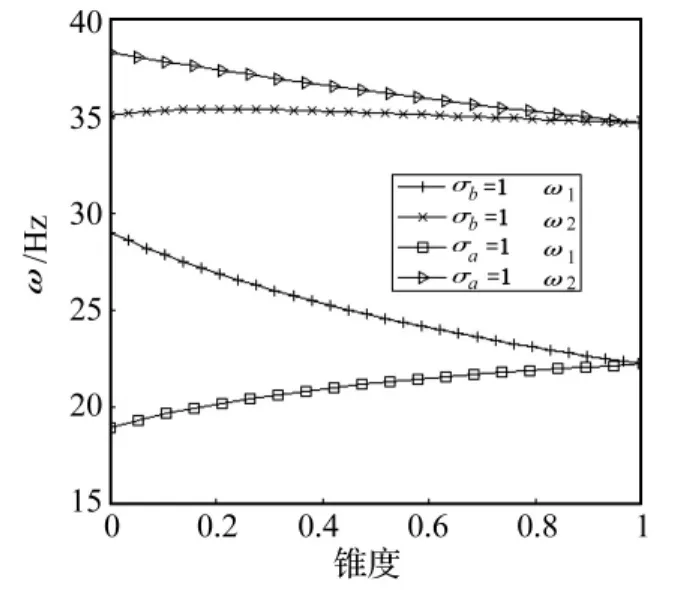
圖9 CUS 構型梁 ω1，ω2隨錐度變化規律Fig.9 ω1 and ω2 vs taper ratio of CUS beam

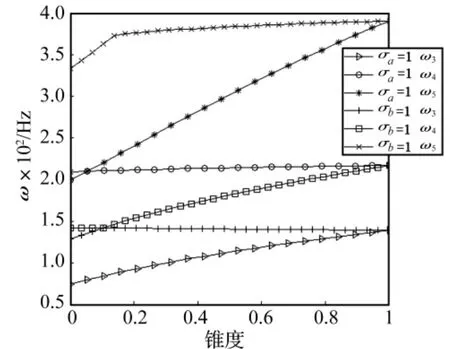
圖10 CUS 構型梁 ω3，ω4，ω5隨錐度變化規律Fig.10 ω3，ω4 and ω5 vs taper ratio of CUS beam

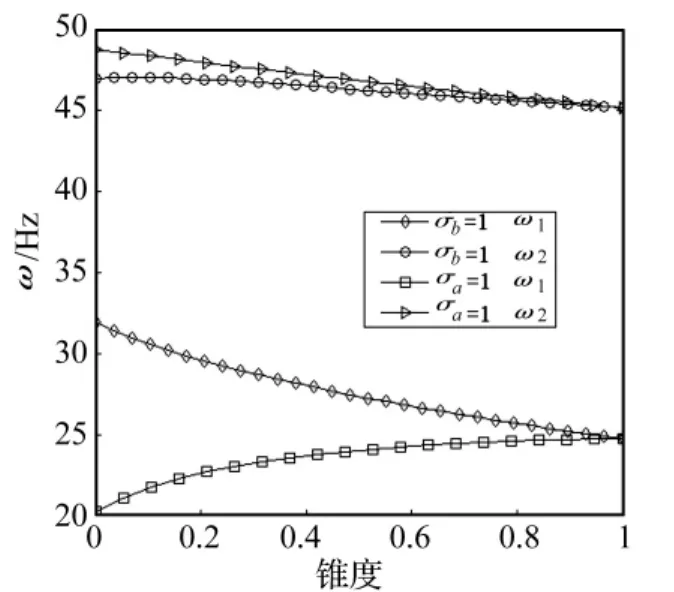
圖11 CAS構型梁 ω1，ω2隨錐度變化規律Fig.11 ω1 and ω2 vs taper ratio of CAS beam

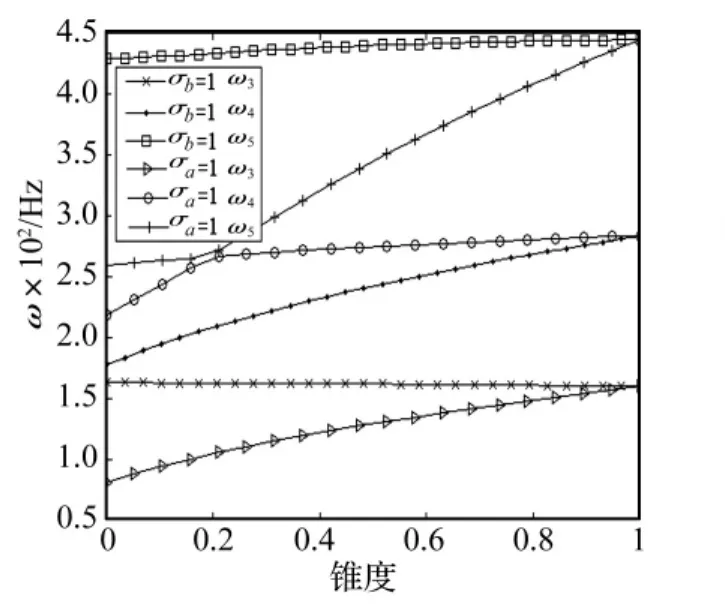
圖12 CAS 構型梁 ω3，ω4，ω5隨錐度變化規律Fig.12 ω3，ω4 and ω5 vs taper ratio of CAS beam

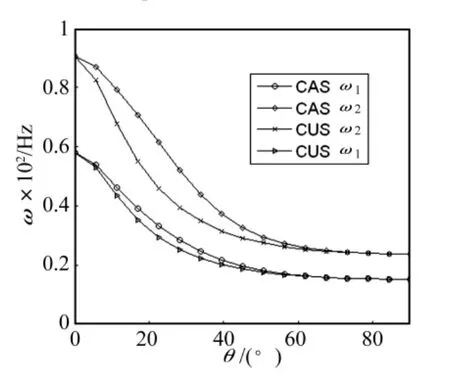
圖13 ω1和 ω2隨鋪層角度變化規律Fig.13 ω1 and ω2 vs ply angel

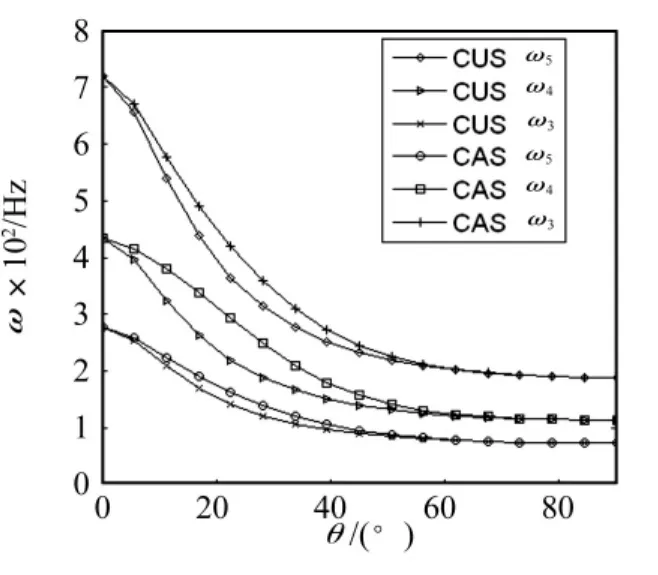
圖14 ω3，ω4和 ω5隨鋪層角度變化規律Fig.14 ω3，ω4 and ω5 vs ply angel

圖13和圖14說明了在錐度σa=σb=0.5的條件下，CAS和CUS構型梁前五階固有頻率隨鋪層角度的變化規律。兩種構型梁的前五階固有頻率隨鋪層角度的變化規律都是下降曲線，由文獻［17］可知，CUS構型的前五階振動為彎曲振動模態和拉扭耦合振動模態中的一種，而CAS構型梁為彎曲為主的振動模態。由鋪設方式可知，采用0°和90°鋪層時，CUS和CAS配置方式實質是相同的，因此固有頻率應該相等。圖12和圖13中，CUS和CAS構型的曲面在0°和90°時相交與實際情況相符。而其它角度鋪層時，CAS構型的固有頻率要大于CUS構型的固有頻率，在20°左右時，差別最顯著。因此將20°時，錐梁和等直梁的固有頻率值列于表2中。可見錐度對于固有頻率值存在著顯著的影響，表3則從具體數值上說明鋪層角度和鋪層方式對于固有頻率的影響。

需要說明的是，Gakerkin法求解的固有頻率的精度與保留模態個數有關。固有頻率隨保留模態數的變化情況列于表4中。可見，CUS與CAS構型梁的各階固有頻率求解精度與保留模態數的關系不完全相同。且不同階的固有頻率隨模態數增加，收斂情況也不相同。對于低階的固有頻率值保留較少的模態數就達到較高的精度，而對于高階固有頻率值則需要保留較多的模態以達到足夠的精度。

因為薄壁結構梁在ANSYS中采用線性殼單元SHELL99，設定鋪層方式和材料性能參數及約束，將圖2中的錐度σa=σb=0.5，鋪層角度為20°的梁劃分為1416個四邊形單元進行分析。ANSYS有限單元法和Galerkin法保留四階模態的求解結果列于表5中。由表5可知，CUS和CAS構型梁的低階固有頻率值與ANSYS求解結果非常接近。充分說明本文建立的運動微分方程和采用Galerkin法求解的正確性。此外表中CAS構型梁的第三階和第五階固有頻率值與有限單元法的求解結果差值較大，原因為保留模態數較少。若增加保留模態數，則差值會明顯降低。

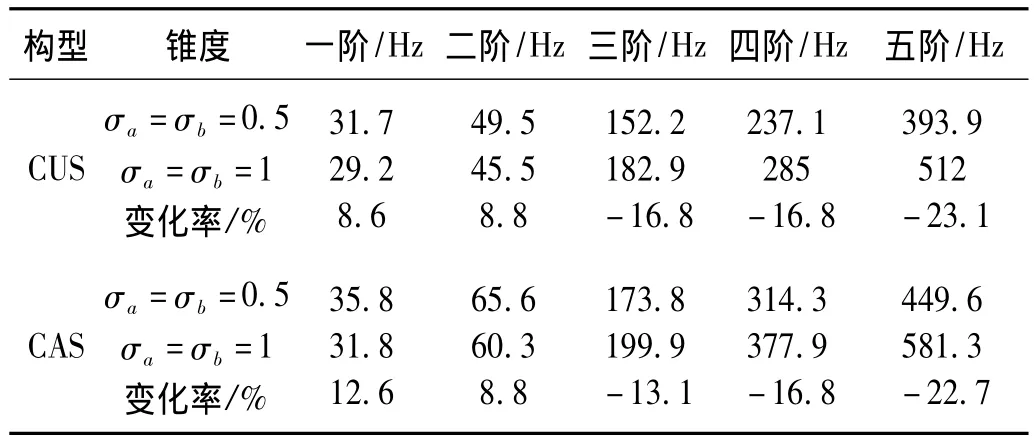
表2 20°鋪層時CAS與CUS梁前五階固有頻率Tab.2 The first five natural frequency of CUS and CAS beams with 20°ply angel

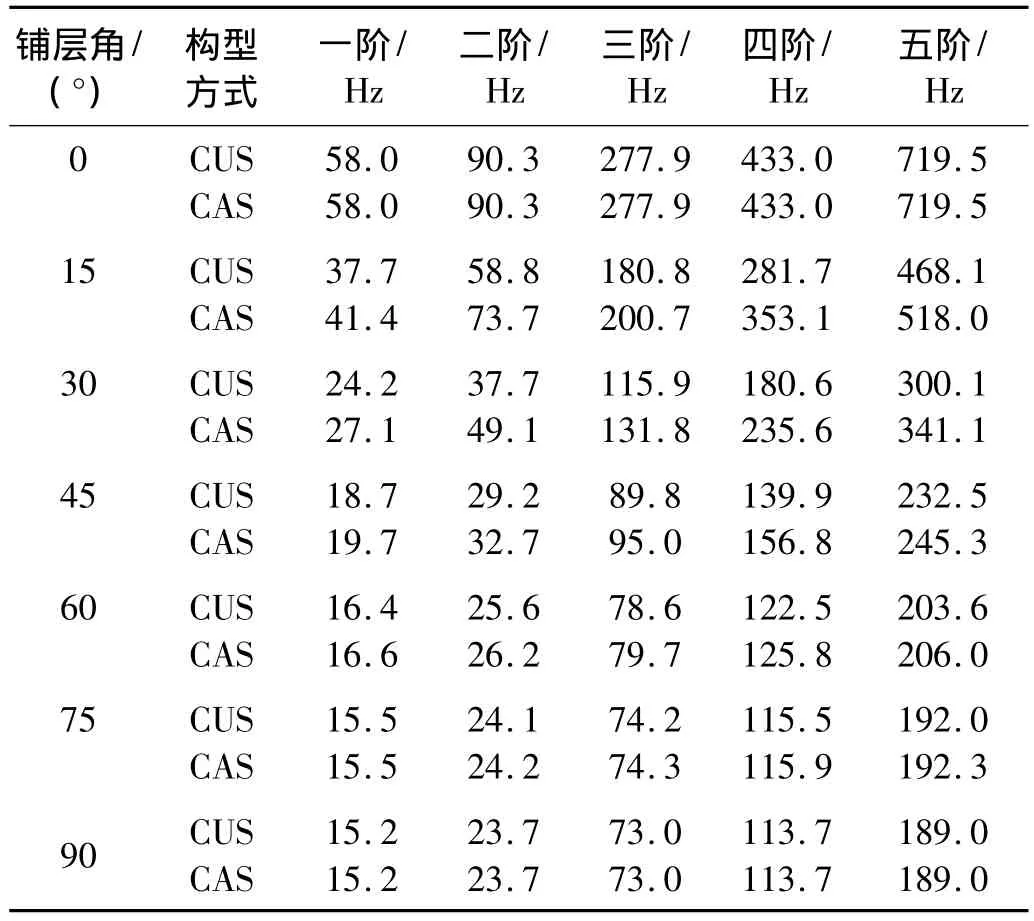
表3 σa=σb=0.5時CAS與CUS梁前五階固有頻率Tab.3 The first five natural frequency of CUS and CAS beams with σa=σb=0.5

表4 模態個數對于固有頻率的影響(σa=σb=0.5，θ=20°)Tab.4 Effect of the number on natural frequencies(σa=σb=0.5，θ=20°)

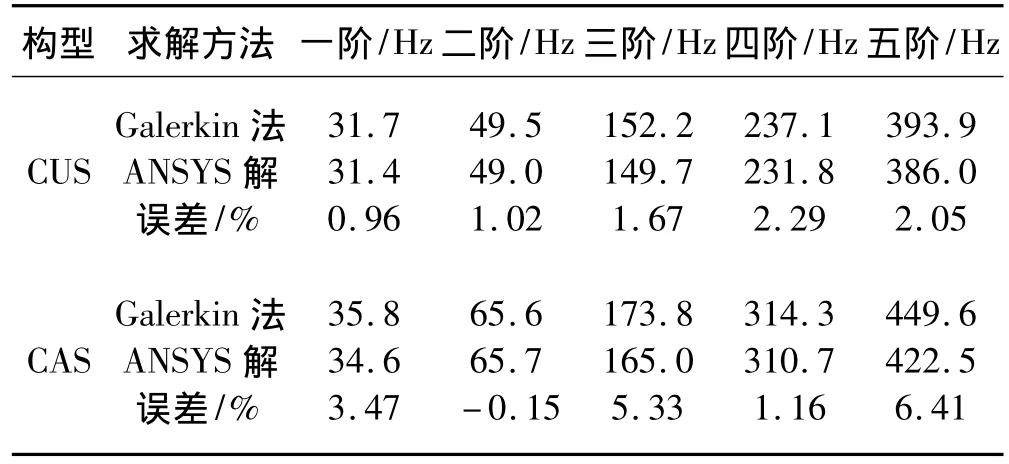
表5 Galerkin法和有限單元法計算結果(σa=σb=0.5，θ=20°)Tab.5 Solution of Galerkin method and finite element method(σa=σb=0.5，θ=20°)

3 結論

采用拉格朗日方程推導了任意封閉變截面薄壁復合材料梁的自由振動方程。該方程適用于沿截面周線剛度任意變化的變截面直梁。應用該方程使用Galerkin法求解了兩種鋪層方式的復合材料梁的固有頻率。有限單元法的求解結果和理論分析解析結果一致，說明了所建立公式的正確性。此外求解結果也反映了薄壁復合材料錐形梁自由振動的彈性耦合機制。說明不同的鋪設方法將引起不同的耦合振動，即使是同樣的鋪設方法，采取不同鋪設角度和不同的錐度，對于固有頻率也存在影響。這些結果對于風力機葉片等工程結構的設計，都具有指導意義。

［1］Barbero E J.Introduction to composite material design［M］.Taylor＆ Francis Inc.，Philadelphia，1999.

［2］Jonesm P M.Mechanics of composite materials［M］.Taylor＆ Francis Inc.，Philadelphia，1999.

［3］Mansfield E H，Sobey A J.The fiber composite helicopter blade.Part I:stiffness properties.Part II:prospects of aeroelastic tailoring［J］.Aeronaut Quart，1979，30:413－449.

［4］Mansfield E H.The stiffness of a two-cell anisotropic tube［J］.Aeronaut.Quart，1981，32:338 － 353.

［5］Kapania R K，Raciti S.Recent advances in analysis of laminated beams and plates 1.shear effects and buckling［J］.AIAA，1989，27(7):923 －934.

［6］Libove C.Stresses and rate of twist in single cell thin-walled beams with anisotropic walls［J］.AIAA ，1988，26(9):1107－1118.

［7］Librescu L，Song O.On the aeroelastic tailoring of composite aircraft swept wings modeled as thin-walled beam structures［J］.Compos Eng，1992，2(5 －7):497 －512.

［8］Song O，Librescu L.Free vibration of anisotropic composite thin-walled beams of closed cross-section contour［J］.Sound Vibr，1993，167(1):129 －147.

［9］Bhaskar K，Librescu L.A geometrically non-linear theory for laminated anisotropic thin-walled beams［J］.Eng Sci，1995，33(9):1331－1344.

［10］Qin Z， Librescu L. On a shear-deformable theory of anisotropic thin-walled beams:further contribution and validations［J］.Compos Struct，2002，56(4):345 － 358.

［11］Na S S，Librescu L.Dynamic response of elastically tailored adaptive cantilevers of non-uniform cross section exposed to blast pressure pulses［J］.Impact Eng，2001，25(9):847－867.

［12］Librescu L，Na S S.Active vibration control of doubly tapered thin-walled beams using piezoelectric actuation［J］.Thin-Walled structures，2001，39:65 －82.

［13］Na S S，Librescu L.Dynamic behavior of aircraft wings modeled as doubly-tapered composite thin-walled beams［C］.Recent Advances in Solids and Structures，New York:ASME，1999(398):59 －68.

［14］Chandiramani N K，Librescu L，Shete C D.On the freevibration of rotating composite beams using a higher-order shear formulation［J］.Aerospace Science and technology，2006(6):545－561.

［15］Zhao Y H，Hu H Y.Structural modeling and aeroelastic analysis of high-aspect-ratio composite wings［J］.Chinese journal of aeronautics，2005，18(1):25－30.

［16］Armanios E A，Badir A M.Free vibration analysis of anisotropic thin-walled closed-section beams［J］.AIAA J，1995，33(10):1905－1910.

［17］Dancila D S，Armanion E A.The influence ofcoupling on the free vibration of anisotropic thin-walled closed-section beams［J］.Int.J.Solids Structures，1998，35(23):3105 － 3119.

［18］易 中，周麗珍.分析力學初步［M］.北京:冶金工業出版社，2006:38－42.

［19］Thomsen J J.Vibrations and stability:advanced theory，analysis，and tools［M］.Springer-Verlag:Berlin-Heidelberg-New York，2003.

［20］Meirovitvh L.Computational methods in structural dynamics［M］. Sijthoff-Noordhoff:Alphen aan den Rijn， The Netherlands，1980.

［21］Hodges D H ，Dowell E H，Nonlinear equations of notion for the elastic bending and torsion of twisted nonuniform rotor blades［R］.NACA TND －7818，1974.