斜拉索基頻識別技術

(華南理工大學土木與交通學院，廣東廣州 510640)

0 引言

近十年來，斜拉橋在國內已成為主要橋型之一，在施工及后期運營狀態中有一項重要的內容，就是索力的測量，索力測量的方法有:油壓表法、壓力環測量法、頻率法等。前兩種是直接測量法，后一種是間接法。這些方法均在實橋中有應用［1］，其中精度較高的有壓力環測量法以及頻率法。壓力環測定:直接在斜拉索錨頭下安裝壓力環，一側靠錨具，另一側靠錨墊板，這種方法最直接，精度高，但成本高，對錨墊板平整度要求高，儀器重不便于操作。頻率法:通過在斜拉索上安裝加速度傳感器，獲取斜拉索在自然振動激勵下的時程曲線，經低通濾波、放大信號和快速傅里葉變換，得到自功率頻譜圖來確定斜拉索的自振頻率，然后由相應公式計算索力。頻率法測索力的優點:安裝測量簡單，設備可多次使用，根據現有儀器水平及分析技術，測定拉索頻率的精度可達到 0.002 Hz，即索力值精度可達 0.6 t～1.2 t，足以滿足工程要求。頻率法適用于沒有預先安裝傳感器情況的現役斜拉橋的索力測量，精度高，測試速度快［2］。頻率法測索力是目前確定斜拉橋索力最廣泛使用的一種方法［3］，作為一種由頻率間接換算索力的方法，振動法測索力的關鍵在于如何由實測數據得到正確的拉索頻率值以及準確的索力、頻率對應關系。

1 工程概況

崖門大橋是廣東省西部沿海高速公路建設項目的重點工程之一，大橋為雙塔單索JP2面預應力混凝土斜拉橋，采用塔梁固結柔性墩體系［4］。每側邊跨設置一個輔墩，跨徑組合為(50+115+338+115+50)m，全橋總長668 m。主梁是單箱五室預應力混凝土梁，梁高3.48 m，橋面全寬26.8 m，設雙向四車道。主墩為雙壁柔性墩，橫向寬12 m，雙壁之間中心距6 m，墩高47.6 m。橋面以上塔柱高73.5 m，塔柱斷面為單箱混凝土斷面。全橋共有斜拉索200根，主梁標準索距6 m，橋型布置圖見圖1。

圖1 崖門橋橋跨布置圖（單位：m）

本文采用壓電加速度傳感器LC0406進行斜拉索振動測試，生產廠家為朗斯測試技術(秦皇島北戴河)有限公司，測試系統框圖見圖2。

用上述測試系統分別于2007年，2008年，2010年，2012年對該橋索力進行通測，2007年測試結果作為長期監控初始值;傳感器置于橋面以上2 m左右，測試值為加速度時程曲線，方向垂直于索線;測試參數［5-8］:采樣頻率80 Hz，低通濾波50 Hz，采樣時間204.8 s，FFT 點數 1024，重疊率 3/4。

圖2 崖門大橋索力測試系統

2 斜拉索基頻識別

根據文獻［9］［10］，當拉索索力一定的時候，理想的情況其經過FFT變換得到的自功率譜上的峰值應該是等間距的，且峰值間距應該等于斜拉索振動的基頻。這是因為理想的斜拉索索力與其自振頻率關系公式知，當索力一定時，高階頻率是基頻的整數倍。在一般的測試環境下，由于各種干擾，在低頻部分往往出現不了頻譜峰值，以前在現場測試時的做法通常是:不考慮自振頻率的階數，僅計算功率譜上比較明顯的相鄰峰值間距，以此作為拉索的基頻值。但實際上，由于斜拉索存在一定的抗彎剛度等原因，導致實測拉索頻率階數越高，頻差越大。如圖3所示，為一根短索的自功率譜圖，根據峰值間間距可判斷第一峰值即為其基頻值。因為短索由于其基頻較大(大于2 Hz)，與橋面震動不容易混疊，故能從頻譜圖上清晰地識別出來。即該索基頻為2.03。

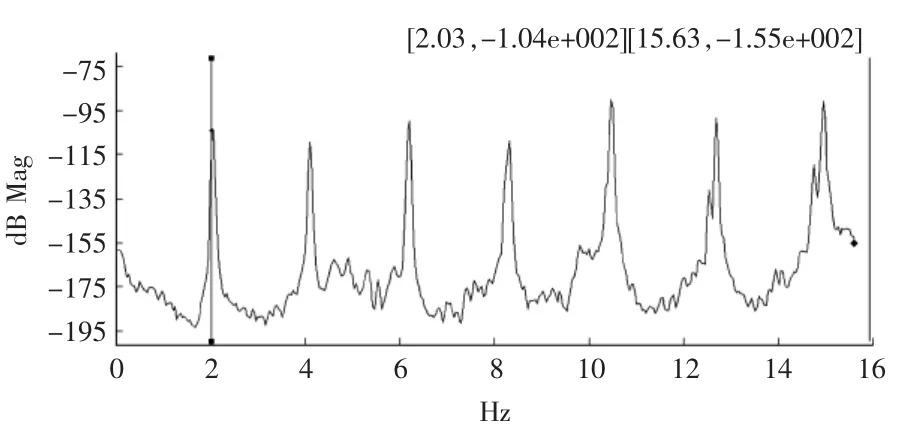
圖3 自功率譜密度（一）

另外，將頻譜圖峰值相減，結果見表1，可明顯看出峰值間距越往高階越大，識別出的基頻誤差越大，從而影響了索力測量的精度(基頻變化0.01，計算出的索力值變化4 t～6 t)。

由于測試條件限制，索力測試時傳感器只能放在索離地面2 m處，環境振動功率譜代表前幾階頻率的峰值很容易混淆，所以難以從頻譜圖上直接看出基頻值，甚至無法確定功率譜上的峰值對應的固有頻率的階數。這是由于較長斜拉橋的拉索的基頻相當低，其功率譜的低頻部分有時涉及與橋面板或橋塔的基頻的耦合。從頻譜圖上難以觀察出其基頻的位置，只能識別出其高階頻率，如圖4所示，為一根長索自功率譜密度，其峰值間距約為1.6，故知第一峰值為其二階頻率，其基頻約為3.13/2=1.565(見表2)。

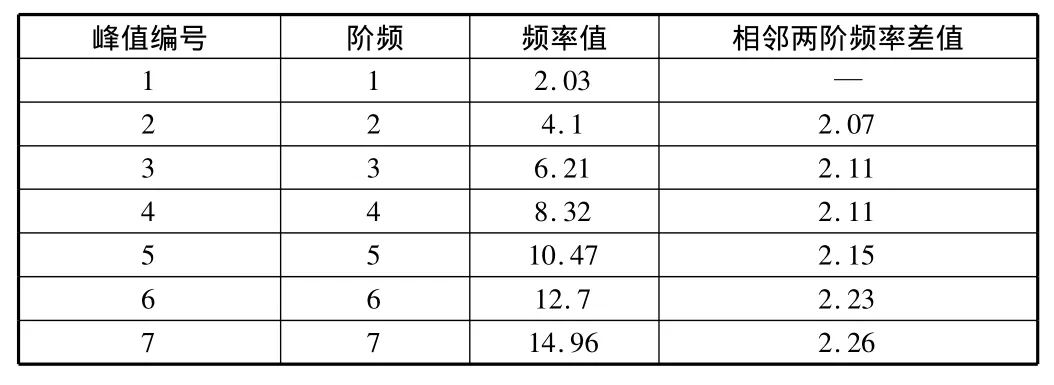
表1 短索自功率譜密度峰值

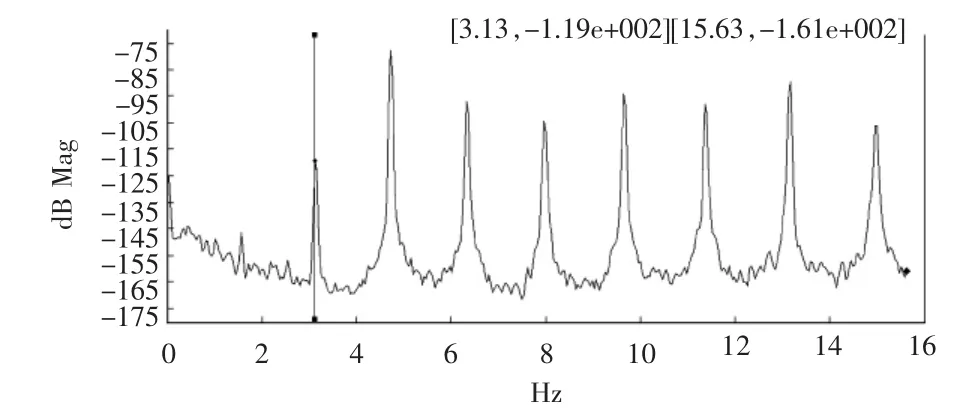
圖4 自功率譜密度（二）

表2 長索自功率譜密度峰值

較長斜拉索的前幾階頻率通常不能被識別，但直接利用高階頻率差值，或用高階頻率除以其階數求基頻就會造成基頻識別值偏大(用7階頻率計算出的基頻比實際基頻大0.23)，導致計算出索力值偏大，故本文采用二次擬合的方法計算其前幾階的頻率。

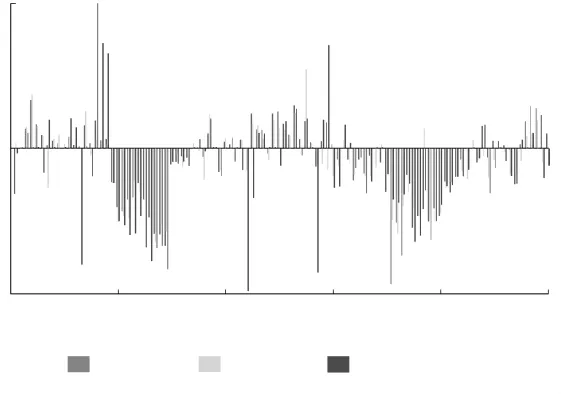
圖5a)是東塔上游25號索的各階頻率擬合結果，從頻譜圖識別第4階～第20階頻率，以二次曲線進行擬合。實測的和擬合的各階頻率差值見圖5b)。可見，實測各階頻率的差值最小為0.703 Hz，最大為0.79 Hz，且各階頻率差值的分布無序;而擬合的各階頻率的差值變化是平緩的，從0.731 Hz～0.767 Hz，與文獻［11］的結論較為吻合。

3 識別結果

運用上述基頻識別方法及文獻［1］中所推導的索力計算公式，對崖門大橋三次長期監控的索力測試結果(2008年，2010年，2012年，僅給出上水測量值)列于圖6，圖7。從圖6，圖7中可以看出:1)橋梁全橋的索力分布比較均勻、對稱;2)三次的索力測試結果的變化率均不大，在5%之內;3)個別斜拉索的變化率較大，可能是由于測試過程中有重車經過，造成一定的誤差。

圖6 上水斜拉索索力對比圖

4 結語

通過頻率識別和索力識別結果，可知主梁和索在0 Hz～3 Hz范圍內有共振現象;二次擬合法比頻率間距法能更準確地識別出較長拉索的低階頻率;在垂度不大的斜拉索索力測量中，可用拋物線代替懸鏈線，具有足夠的精度。崖門大橋的中跨斜拉索索力分布比較對稱均勻，測量結果可靠;總體來看，由于混凝土收縮徐變作用，主塔周圍的短索索力趨向于減小，而長索索力趨向于變大。個別索索力變化較大，可能是受到測試環境的影響，或是出現松弛，應該多次測試予以確認，保證橋梁結構安全。

［1］王衛鋒.PC斜拉橋的施工監測［D］.廣州:華南理工大學博士論文，2000.

［2］郭良友，林一寧，李文波，等.武漢長江二橋的索力、溫度和應力測量［J］.橋梁建設，1995(3):44-53.

［3］蘇 成，徐郁峰，韓大建.頻率法測量索力中的參數分析與索抗彎剛度的識別［J］.公路交通科技，2005，22(5):75-78.

［4］華南理工大學城市建設研究中心.廣東省西部沿海高速公路崖門大橋施工監控工作總結［R］.2002.

［5］王衛鋒，徐郁峰，韓大建，等.崖門大橋施工中的索力測試技術［J］.橋梁建設，2003(1):23-26.

［6］戴詩亮.隨機振動實驗技術［M］.北京:清華大學出版社，1984.

［7］吳天毅.測試技術與測試信號處理［M］.北京:清華大學出版社，1991.

［8］張阿舟.實用振動工程(3)——振動測量與試驗［M］.北京:航空工業出版社，1997.

［9］韓 鋒，申彥鵬.基于傅里葉變換的斜拉索振動頻率識別研究［J］.西部交通科技，2010(7):91-92.

［10］陳 剛，任偉新.基于環境振動的斜拉橋拉索基頻識別［J］.地震工程與工程振動，2003(3):23-24.

［11］侯立群，歐進萍，趙雪峰，等.哈爾濱四方臺斜拉橋模態參數和索力識別［J］.振動與沖擊，2009，28(5):106-110.